Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

S. van der Hoeven, B.J. Boersma, and D.J.E.M. Roekaerts

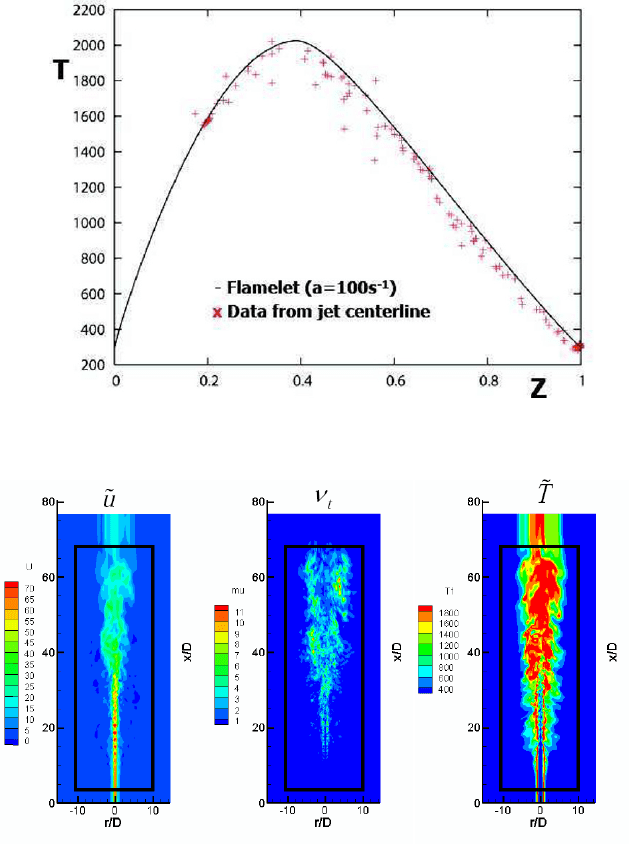
Fig. 9 The ﬂamelet model temperature proﬁle as a function of the mixture fraction Z (solid line),

and the local centerline temperature obtained from the LES model (dots).

Fig. 10 Instantaneous plots of resolved axial velocity (left), eddy viscosity (middle) and resolved

mixture fraction (right).

Mach number LES [7] in combination with steady ﬂamelet modeling. Better results

are expected when the present model is combined with a more precise representation

of the turbulent inﬂow.

284

Large Eddy Simulation of Jet Flames

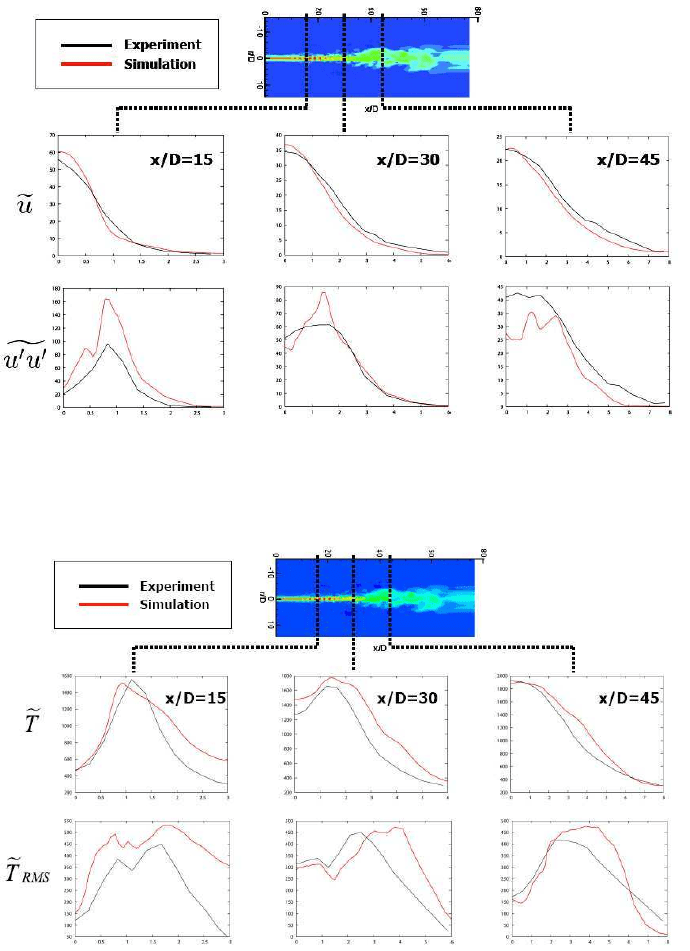
Fig. 11 Radial proﬁles of the time averaged axial velocity and the variance of axial velocity at

three axial positions.

Fig. 12 Radial proﬁles of the time averaged temperature and the standard deviation of temperature

at three axial positions.

285

S. van der Hoeven, B.J. Boersma, and D.J.E.M. Roekaerts

7 Summary and conclusions

A new compressible combustion code for DNS/LES of turbulent non-premixed jet

ﬂames has been developed, based on a high-order compact ﬁnite difference formu-

lation. The Favre-ﬁltered transport equations were solved and the SGS ﬂuxes were

closed with a constant Smagorinksy model. The steady ﬂamelet model was used for

the chemistry. In order to couple the ﬂamelet solution with the compressible code a

relaxation term was added to the total non-chemical energy equation. Special atten-

tion was given to the treatment of the computational boundaries. We propose adding

a convective term with supersonic velocity in a small region near the in- and out-

ﬂow boundaries together with explicit ﬁltering of the velocity. Using this approach

it was observed that the simulation kept on running stable and reﬂections where too

low to have an effect on the interior domain. Furthermore, the computational costs

(measured in time) compared to the NSCBC method were reduced with a factor 1.5-

2.0 for this simulation conﬁguration. Nevertheless, it must be mentioned that such a

comparison depends strongly on the simulation parameters (number of grid points,

number of processors, number of open boundaries) and the implementation (numer-

ical efﬁciency and used algorithms). To obtain better agreement with experimental

results a more accurate representation of the turbulent inﬂow conditions is needed.

8 Acknowledgements

The Dutch national computing facilities foundation NCF is acknowledged for the

allotted computing time on the TERAS/ASTER system, under project nr. SG-07-

279.

References

1. B.J. Boersma, A staggered compact ﬁnite difference approach for the compressible Navier-

Stokes equations, J. Comp. Phys., 208, 675, (2005)

2. S.K. Lele, Compact ﬁnite differences with spectral-like resolution, J. Comp. Phys., 103, 16,

(1992)

3. P. Chu, C. Fan, A three point combined compact difference scheme, J. Comp. Phys., 140, 370,

(1998)

4. S. Nagarajan, S.K. Lele, J.H. Ferziger, A robust high-order compact method for large eddy

simulation, J. Comp. Phys., 191, 392, (2003)

5. R.W.C.P. Verstappen, A.E.P. Veldman, Symmetry-preserving discretization of turbulent ﬂow,

J. Comp. Phys., 187, 343, (2003)

6. International Workshop on Measurement and Computation of Turbulent Nonpremixed Flames,

http://www.ca.sandia.gov/TNF/DataArch/FlameD.html

7. H. Pitsch, H. Steiner, Large-eddy simulation of a turbulent piloted methane/air diffusion ﬂame

(Sandia ﬂame D), Phys. Fluids., 12, 2541, (2000)

8. N. Branley, W.P. Jones, Large Eddy Simulation of a turbulent non-premixed ﬂame, Comb.

Flame, 127, 1914-1934, (2001)

286

Large Eddy Simulation of Jet Flames

9. T. Poinsot, S.K. Lele, Boundary conditions for direct simulations of compressible viscous

ﬂows, J. Comp. Phys., 101, 1042 (1992)

10. C.S. Yoo, Y. Wang, A. Trouve, H.G. Im, Characteristic boundary conditions for direct simula-

tions of turbulent counterﬂow ﬂames, Comb. Th. Mod., 9, 617-646, (2005)

11. T. Colonius, S.K. Lele, P. Moin, Boundary conditions for direct computation of aerodynamic

sound computation, AIAA Journal, 31, 1574-1582, (1993)

12. S. Ta’asan, D.M. Nark, An absorbing buffer zone technique for acoustic wave propagation,

AIAA Paper 1995-0146, (1995)

13. J.P. Berenger, A perfectly matched layer for the absorption of electromagnetic waves, J. Comp.

Phys., 114, 185-200, (1994)

14. J.B. Freund, Proposed inﬂow/outﬂow boundary condition for direct computation of aerody-

namic sound, AIAA Journal tech. notes, 34, 740-742, (1997)

15. D.J. Bodony, S.K. Lele, Jet noise prediction of cold and hot subsonic jets using Large-Eddy

Simulation, AIAA Paper 2004-3022 (2004)

16. N. Peters, Turbulent Combustion, Cambridge University Press (2000)

17. K.K. Kuo, Principles of Combustion, John Wiley and sons (2005)

18. T. Poinsot and D. Veynante, Theoretical and Numerical Combustion, R.T. Edwards Inc. (2005)

19. R.A. Vreman, An eddy-viscosity subgrid-scale model for turbulent shear ﬂow: Algebraic the-

ory and applications, Phys. Fluids, 16, 3670 (2004)

20. P.J. Coelho, O.J. Teerling and D. Roekaerts, Spectral radiative effects and turbulence/radiation

interaction in a non-luminous turbulent jet diffusion ﬂame, Combust. Flame, 133, 75-91,

(2003)

21. A. Habibi, B. Merci and D. Roekaerts, Turbulence/radiation interaction in RANS simulations

of non-premixed piloted turbulent laboratory scale ﬂames, Combust. Flame, 151, 303-320,

(2007)

287

A Suite of Mathematical Models for Bone

Ingrowth, Bone Fracture Healing and

Intra-Osseous Wound Healing

F.J. Vermolen, A. Andreykiv, E.M. van Aken, J.C. van der Linden, E. Javierre, and

A. van Keulen

Abstract In this paper, some modeling aspects with respect to bone ingrowth, frac-

ture healing and intra-osseous wound healing are described. We consider a ﬁnite el-

ement method for a model of bone ingrowth into a prosthesis. Such a model can be

used as a tool for a surgeon to investigate the bone ingrowth kinetics when position-

ing a prosthesis. The overall model consists of two coupled models: the biological

part that consists of non-linear diffusion-reaction equations for the various cell den-

sities and the mechanical part that contains the equations for poro-elasticity. The two

models are coupled and in this paper the model is presented with some preliminary

academic results. The model is used to carry out a parameter sensitivity analysis

of ingrowth kinetics with respect to the parameters involved. Further, we consider

a Finite Element model due to Bailon-Plaza and Van der Meulen for fracture heal-

ing in bone. This model is based on a set of coupled convection-diffusion-reaction

equations and mechanical issues have not been incorporated. A parameter sensitiv-

ity analysis has been carried out. Finally, we consider a simpliﬁed model due to

Adam to simulate intra-osseous wound healing. This model treats the wound edge

as a moving boundary. To solve the moving boundary problem, the level set method

is used. For the mesh points in the vicinity of the wound edge, a local adaptive mesh

reﬁnement is applied.

F.J. Vermolen, E.M. van Aken, E. Javierre

Delft Institute of Applied Mathematics, Faculty of Electrical Engineering, Mathematics and Com-

puter Science, Delft University of Technology, Mekelweg 4, 2628 CD Delft, The Netherlands

e-mail: F.J.Vermolen@tudelft.nl,

A. Andreykiv, J.C. van der Linden, F. van Keulen

Mechanical, Maritime and Materials Engineering, Delft University of Technology, Mekelweg 2,

2628 CD Delft, The Netherlands e-mail: A.Andreykiv@tudelft.nl

289

Lecture Notes in Computational Science and Engineering 71,

DOI 10.1007/978-3-642-03344-5_10,

B. Koren and C. Vuik (eds.), Advanced Computational Methods in Science and Engineering,

F.J. Vermolen et al.

1 Introduction

In osteoporosis, fracture risk is high, after a hip fracture a prosthesis that replaces

the joint is often the only remedy. In the case of osteoarthritis and rheumatoid arthri-

tis, the cartilage degrades and moving the joints becomes painful. Ultimately, most

patients will receive a prosthesis to restore the function of a diseased joint. Pros-

theses are usually attached to the host bone by means of surgical screws to obtain

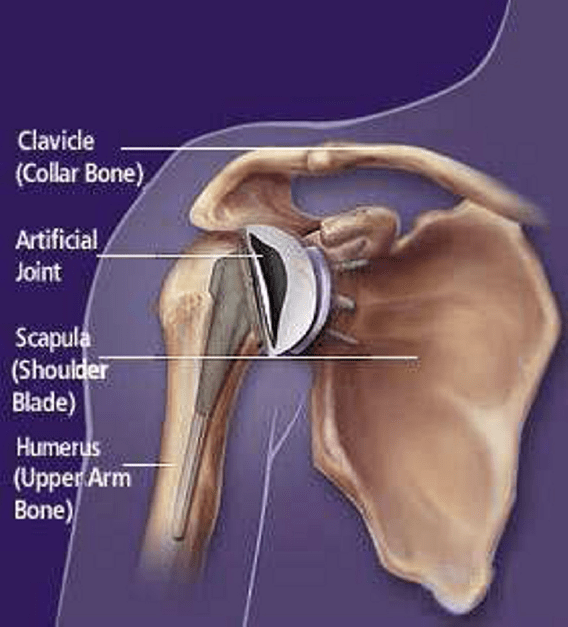
sufﬁcient initial stability. A schematic of a prosthesis of the shoulder cavity, embed-

ded within an artiﬁcial joint is shown in Figure 1. In the course of time, bone will

grow into a porous tantalum layer and hence more stability of the prosthesis is ob-

tained. To investigate the quality and life time of such an artiﬁcial joint, one needs

to study the effects of the placement of the prosthesis and of the materials that are

involved in the joint. At present, these effects are often studied using large amounts

of data derived from patients. To predict the life span and performance of artiﬁcial

joints, numerical simulations are of great value since these simulations give many

qualitative insights by means of parameter sensitivity analysis. These insights are

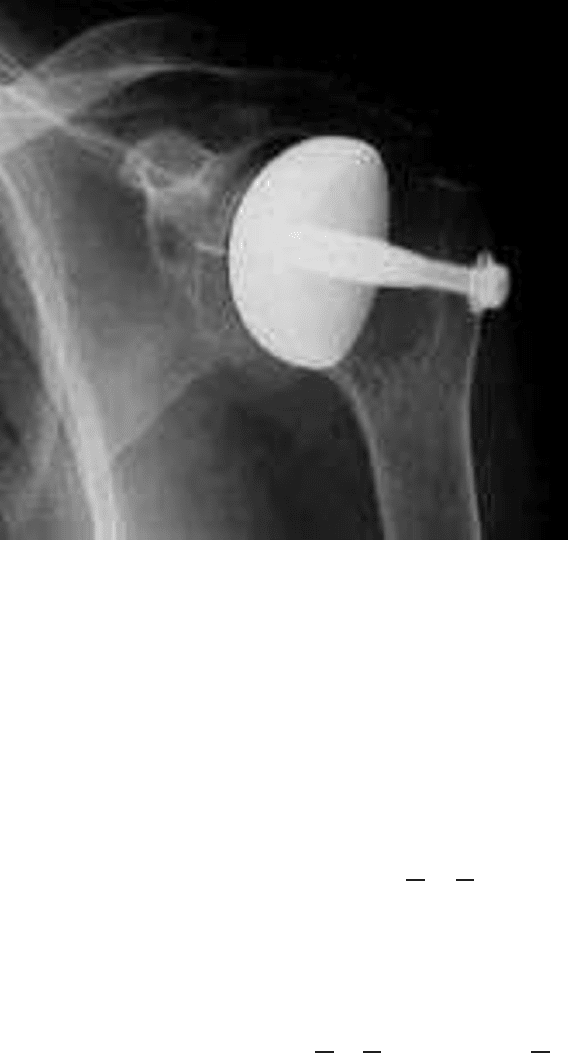
hard to obtain by experiments. In Figure 2, an X-ray picture of the prosthesis of the

shoulder cavity is shown.

In the case of a shoulder prosthesis, the angle at which the prosthesis is posi-

tioned by the surgeon is crucially important. The angle is important for the ability

of moving the arm by the patient, but also to have the right strain pattern for (op-

timal) bone ingrowth. The latter fact is due to the fact that the mammalian bone is

only generated if a certain strain is exceeded, but also smaller than a certain upper

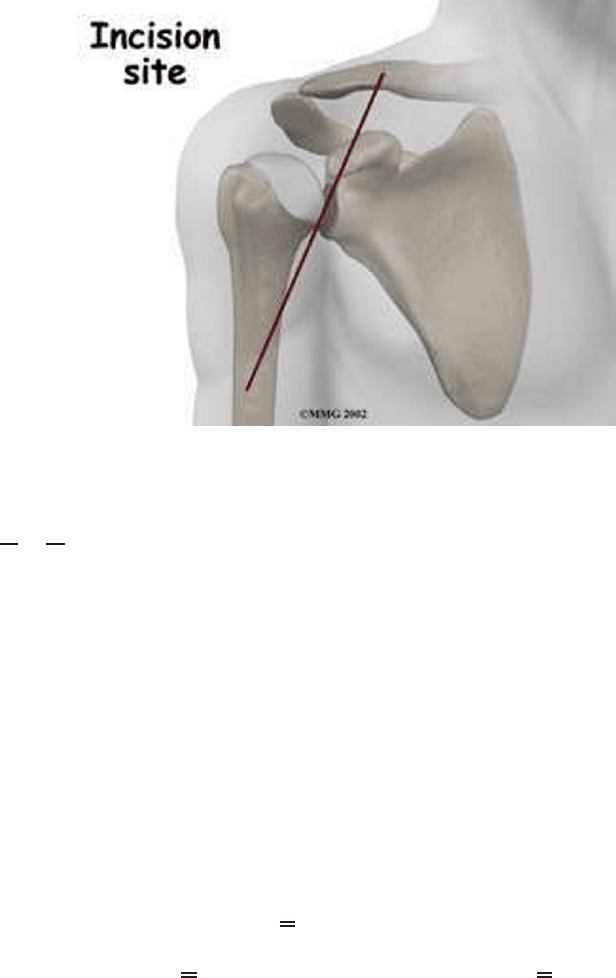
bound. For the surgery on the shoulder, the incision on the shoulder is made at the

front in order to save crucial organs and muscles of the patient. The location of the

incision is shown in Figure 3.

As a result of a limited visibility of the orthopaedic surgeon, the angle of place-

ment of the prosthesis is a crucial issue. Currently the stress and strain behavior

of the shoulder blade is studied at the Delft University of Technology, using three-

dimensional Finite Element simulations as a function of the angle of placement of

the prosthesis. An example of a computational domain is shown in Figure 4.

Several studies have been done to simulate bone-ingrowth or fracture healing of

bones. To list a few of them, we mention the model due to Adam [1], Ament and

Hofer [3], Bailon-Plaza et al. [7], Prendergast et al. [10] and recently by Andreykiv

[4]. The model due to Prendergast et al. and LaCroix et al. [10, 13] will be treated

in more detail, since we expect that this model contains most of the biologically

relevant processes, such as cell division and differentiation, tissue regeneration, and

cell mobility. Many ideas from modeling fracture healing of bones are used in these

models, since bone-ingrowth into a prosthesis resembles the fracture healing pro-

cess. In the model due to Prendergast, the inﬂuence of the mechanical properties on

the biological processes are incorporated. Further, we note that Prendergast’s model

has been compared to animal experiments.

Next to bone-ingrowth into a prosthesis, we present the model due to Bailon-

Plaza and Van der Meulen [7] for fracture healing in bone. This model is not cou-

pled with the equations from (poro-)elasticity. Andreykiv [6] applies the model for

290

Models for Bone Ingrowth and Healing

Fig. 1 An example of a schematic of an artiﬁcial shoulder joint.

bone-ingrowth to fracture healing in which coupling with mechanics has been ac-

complished.

Finally, the issue of intra-osseous wound healing is modeled using the simpliﬁed

formalism due to Adam [1]. An intra-osseous wound may result from surgery (think

of a wound on a skull due to brain surgery) or an injury caused by an accident.

The equations have a rather simple nature, though obtaining a numerical solution is

challenging since the wound edge is treated as a moving boundary.

In this paper, we will see a calibrated existing bone ingrowth model in terms

of a system of nonlinearly coupled diffusion-reaction equations, for which the me-

chanical strain and ﬂuid ﬂow are important input parameters. In order to compute

the aforementioned parameters, the poro-elasticity equations are solved. These two

classes of models will be treated separately. This paper concerns a compilation of

preliminary results, with some data for a shoulder prosthesis. Further, the paper

considers a model for fracture healing in bone and ﬁnally a model for healing of an

intra-osseous wound is described.

291

F.J. Vermolen et al.

Fig. 2 An example of an X-ray picture of the prosthesis of the shoulder cavity.

2 The bone-ingrowth model

We consider a prosthesis for the shoulder cavity. A sketch of the prosthesis is given

in Figure 5. The top part of the prosthesis consists of polyethylene. This part is in

actual contact with the upper arm, which exerts a loading on it. The second part con-

sists of a tantalum mesh and polyethylene. In these two parts, we solve an equation

for mechanical equilibrium combined with Hooke’s Law only. The third part con-

tains the porous tantalum. Into this part, bone ingrowth takes place from the glenoid,

which is the part of the scapula, in which the humeral head rotates. We denote the

entire computational domain by

Ω

, which consists of

Ω

(the elastic domain) and

Ω

(the poro-elastic domain), hence

Ω

∪

Ω

∪(

Ω

∩

Ω

). The overlines

indicate the closure of the (sub) domain. Further, we assume

Ω

and

Ω

to be dis-

joint, that is

Ω

∩

Ω

= /0. The domain

Ω

represents the part of the computational

domain on which only the elastic equations are solved. On

Ω

, one solves the poro-

elastic equations. Further, in

Ω

, we solve the equations for bone-ingrowth, which

is referred to as the biological part of the model.

Further, we note that

Ω

∪

Ω

, where

Ω

and

Ω

are the elastic part of

the prosthesis and bone respectively. Further,

Ω

∩

Ω

are separated by

Ω

, hence

292

Models for Bone Ingrowth and Healing

Fig. 3 The location at which the incision to put the shoulder prosthesis is carried out by the sur-

geon.

Ω

∩

Ω

= /0. The boundary of the computational domain,

Ω

, is denoted by

, and

of the subdomains

Ω

and

Ω

, their respective boundaries are represented by

and

The biological part of the model involving cell growth, division, differentiation

and formation of bone and cartilage, applies for the porous tantalum. The coef-

ﬁcients in the biological part of the model depend on the local strains and ﬂuid

ﬂow velocity, which establishes a nonlinear coupled problem. First, the mechanical

model is presented and subsequently we give the biological model.

2.1 The mechanical model

Assuming mechanical equilibrium in both the poro-elastic part and the elastic part

of the domain, we solve

−div

= f, x ∈

Ω

. (1)

In the above equation,

and f respectively denote the stress tensor





in two dimensions and f represents the internal body force. In our application, we

disregard the internal body force, hence we take f = 0. At a part of the top boundary

of the prosthesis, which is a part of the computational domain, a quadratic loading

is exerted, that is

293

F.J. Vermolen et al.

Fig. 4 A three-dimensional computational domain of the shoulder blade.

·n = t, x ∈

. (2)

Here, t denotes the exerted loading on

, which is the part of

on which the external

loading is applied. On the bottom boundary of the computational domain, which is

on the glenoid, we assume that the displacement is zero, that is

u = 0, x ∈

. (3)

Here

denotes the part of the outer boundary that is ﬁxed to the host bone. On all

the other parts of the boundary, it is assumed that there is no loading, that is

·n = 0, x ∈

∪

). (4)

The material properties vary strongly over the various parts of the computational

domain. The displacement and traction are assumed to be continuous.

294