Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

S. van der Hoeven, B.J. Boersma, and D.J.E.M. Roekaerts

properties are tabulated as a function of resolved mixture fraction and variance of

mixture fraction.

The variance of mixture fraction is estimated with a simple gradient model,

which can be derived from local equilibrium arguments [8]:

Z”

= C

∆

∂

, (21)

with C

being 0.2. Resolved temperature, mean molecular weight, speciﬁc heat

and temperature dependent viscosity are stored in the look up table. The steady

ﬂamelet model (without extinction model) is sufﬁciently accurate to describe the

Sandia ﬂame D, discussed below. At this stage our main focus is on testing the

compressible code in combination with scalar transport rather than on the chemistry

model itself. When using (adiabatic) ﬂamelet methods in low-Mach number codes it

is sometimes possible to replace the energy equation with the ﬂamelet temperature

solution. However, for compressible formulations this cannot be done in general,

due to the presence of ﬁnite acoustic time scales (inﬂuence of pressure variations on

the energy). In order to couple the ﬂamelet solution in the compressible code while

retaining acoustics we use a simple relaxation method to bring the system at the

ﬂamelet temperature solution. The energy equation is solved with the heat release

source term given by a relaxation term:

= −

¯c



T −



, (22)

where

is the ﬂamelet temperature and

is the relaxation time constant. The

effect of using such a ﬂamelet source term was investigated using 1D simulations.

Different values for

were tested. It was observed that when a too small time con-

stant is used stability problems arise due to large ﬂow dilatation and on the other

hand using time constants larger than the integral time scale of the ﬂow results in

inactive behavior (hot gas mixing). It was observed that a time constant of approxi-

mately 15u

/D, where u

is the maximum jet velocity at the inlet and D the nozzle

diameter, works most efﬁciently. Therefore we use this value in the 3D simulations.

4 Numerical method

The LES ﬁlter introduces a certain cut-off in the wave number spectrum, see Figure

1. Wave numbers which are smaller than the cut-off wave number are resolved by

the numerical scheme. Wave numbers which are larger than the cut-off frequency

have to be modelled with a subgrid model. A common approach is to take the cut-

off wave number equal to the grid resolution, the so-called implicit LES ﬁlter. A

better but more elaborate approach is to use an explicit ﬁlter which has a cut-off

wavelength which is larger than the grid resolution. In this paper we will follow the

274

Large Eddy Simulation of Jet Flames

ﬁrst approach, i.e. the grid resolution equals the cut-off wavenumber and hence no

explicit ﬁltering will be performed.

The unresolved (or subgrid scales) are in general responsible for the dissipation

of kinetic energy and also for the diffusion of temperature and species ﬂuctuations.

The main task of any subgrid model is to provide the required dissipation or diffu-

sion rate. Unfortunately, any numerical method will also provide a certain amount

of dissipation of diffusion. In LES the dissipation or diffusion is in general a mix-

ture of numerical diffusion and model diffusion. Numerical diffusion can be very

useful to stabilize computations, but it is in general unwanted, because it does not

only depend on gradients in the ﬂow but also on the quality of the grid.

In this study we will use methods that minimize the numerical diffusion. This

more or less rules out all (low order) upwind methods. Schemes with a purely central

discretization in general do not introduce signiﬁcant numerical dissipation.

4.1 The derivative

In the equations given previously only ﬁrst order spatial derivatives appear. There-

fore, we will only discuss ﬁrst order derivatives. The simplest central scheme for

the 1st derivative is the classical second order scheme, which reads for a function

= f(i

∆

x):

′

i+1

− f

i−1

∆

+ O(

∆

), (23)

where

∆

x is the grid spacing. Here we will assume that the function f

can be written

as a Fourier series

= f(i

∆

x) =

∑

f (k)exp( jki

∆

x), (24)

in which j =

√

−1 is the imaginary unit and k a wave number. With help of this

Fourier series it is easy to derive the error of the ﬁnite difference scheme as a func-

tion of the wavenumber k. The result reads:

error(k

∆

x) = 1 −

sin(k

∆

. (25)

Is is clear that the discretization error made by the scheme is small for small values

of the wavenumber k and rather larger for large values of k. If we use this scheme

for our Large Eddy Simulation, we will have a large error close to the cut-off wave-

length of the LES ﬁlter and therefore this is scheme is unwanted. A simple extension

of the scheme would be to add two points on the right hand side, i.e:

′

i+1

− f

i−1

∆

−

i+2

− f

i−2

∆

+ O(

∆

). (26)

This is the classical fourth order scheme. The error as a function of the wavenumber

k is given by

275

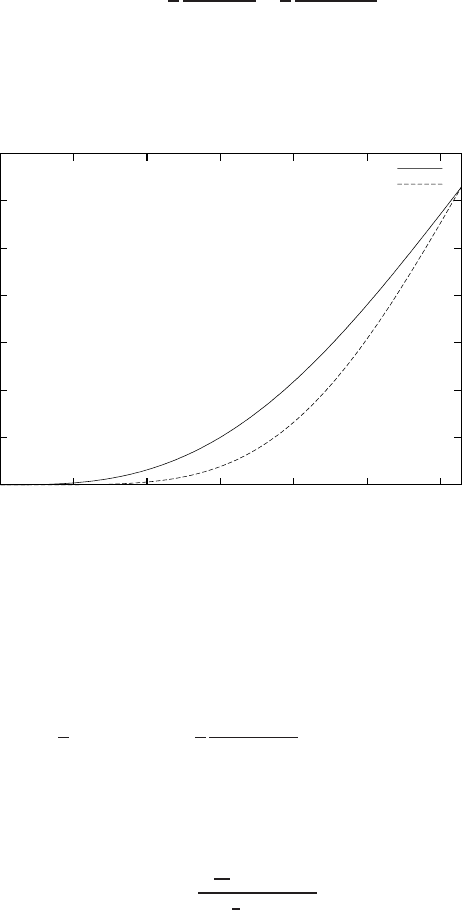
S. van der Hoeven, B.J. Boersma, and D.J.E.M. Roekaerts

error(k

∆

x) = 1 −

sin(k

∆

sin(2k

∆

. (27)

The errors for the second and fourth order scheme, equations (22) and (24), are

plotted in Figure 2. The fourth order scheme is better than the second order scheme

but both are fairly inaccurate for wavenumbers larger than 1.5.

0.5

1.5

2.5

3.5

0 0.5 1 1.5 2 2.5 3

error(k dx)

k dx

2nd order

4th order

Fig. 2 The error as a function of the wave number k

∆

x for a 2nd and 4th order ﬁnite difference

scheme

The numerical accuracy for the large wave numbers can be greatly increased

by using a so-called compact formulation of the ﬁnite difference formulation. This

formulation reads in its most simple form:

′

[ f

′

i−1

+ f

′

i+1

] =

i+1

− f

i−1

∆

+ O(

∆

). (28)

The actual evaluation of this scheme requires the solution of a tridiagonal system

and is therefore computationally more expensive than the standard fourth order

schemes. We can write the following relation for the error

error(k

∆

x) =

sin(k

∆

1 +

cos(k

∆

. (29)

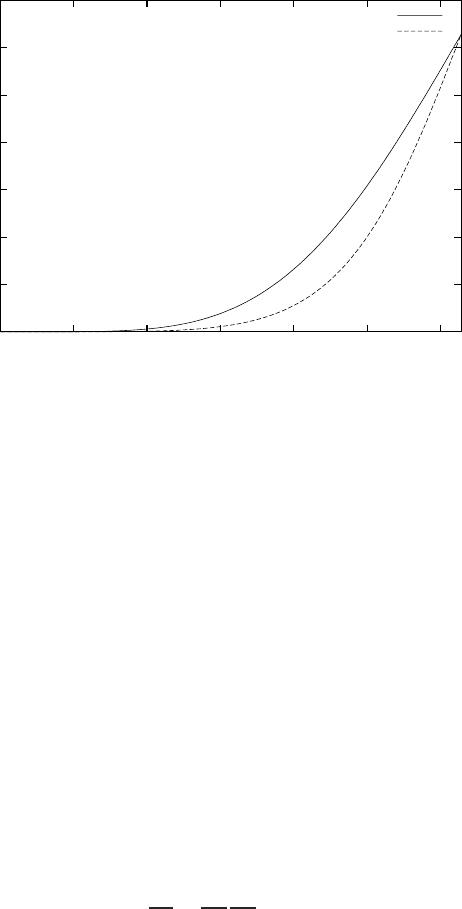
This error is considerably smaller than the error of the central fourth order scheme,

see Figure 3.

In the literature mostly the 6th order compact scheme is used. This scheme is

constructed by adding two additional points to the righthand side of equation (25)

and evaluating the coefﬁcients by a Taylor expansion.

276

Large Eddy Simulation of Jet Flames

0.5

1.5

2.5

3.5

0 0.5 1 1.5 2 2.5 3

error(k dx)

k dx

4th order

4th order compact

Fig. 3 The error as a function of the wave number k

∆

x for a 4th order central and a fourth order

compact scheme.

The drawback of compact schemes for non-linear problems such as the Navier-

Stokes equations is the fact that these schemes are fairly unstable. Due to the low

dissipation error of the numerical scheme it is not possible to ”under resolve” certain

wavelengths. A large eddy simulation is by deﬁnition under resolved and therefore

compact schemes are not very suited for LES. Common practice is to use a high

order compact ﬁlter to remove the short wave instabilities. This type of approach

works but also introduces an artiﬁcial viscosity and is therefore unwanted for large

eddy simulation.

Recently, staggered variants of the compact schemes have been proposed by [4,

1]. These schemes turn out to be much more stable and can be used when the grid

is not sufﬁciently ﬁne to resolve all scales of motion. In this paper we will adopt the

staggered method as proposed in [1]. In this method the vector quantities are stored

at the cell faces and all scalar quantities are stored in the cell centers. Compact

differentiation and interpolation rules are used to calculate the necessary quantities

on the computational grid. This is all done with a 10th order accurate scheme. On

non-uniform grids a mapping of the form

d f

is used. Here x is the non-uniform coordinate,

the uniform coordinate and the ﬁrst

derivatived

/dx is a known analytical function which is non-zero inside the compu-

tational domain. In this way we can calculate the derivatives on a non-uniform grid

without any additional errors. For the interpolation on the non-uniform grids we use

the same rule as for a uniform grid. This is strictly speaking not correct. We have

277

S. van der Hoeven, B.J. Boersma, and D.J.E.M. Roekaerts

chosen for this approach because only in this way we are sure that the discretization

of the ﬁrst-order derivative is purely symmetric and thus does not introduce any arti-

ﬁcial dissipation or diffusion, [5]. The error we make in the interpolation procedure

can be controlled by generating grids with very small differences in mesh widths of

neighboring cells.

4.2 Time discretization

For the time discretization we use a standard fourth order Runge-Kutta method. For

a linear advection diffusion problem the time step limitation for the RK4 scheme is

approximately 2.8 based on a CFL type criterion. For the present problem, which is

strongly non-linear, we use a ﬁxed time step

∆

t the value of

∆

t corresponds roughly

to a CFL number of 1.0.

4.3 The discretization of the Navier-Stokes equations for the

SANDIA ﬂame D problem

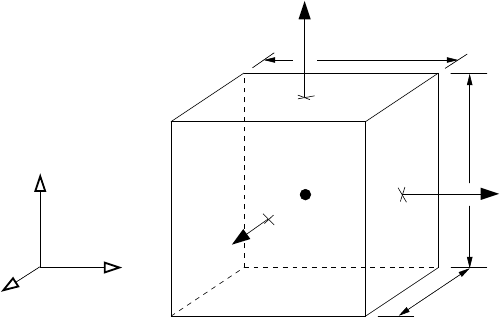
The 3D equations are discretized on a staggered non-uniform Cartesian grid in phys-

ical space. A typical grid volume is shown in Figure 4. The non-uniform grid is

i,j+1/2,k

∆

i,j,k+1/2

y∆

∆z

i,j,k

φi,j,k

ρi,j,k

µi,j,k

i+1/2,j,k

Fig. 4 The layout of the staggered grid. The vector quantities are stored at the cell faces, and the

scalar quantities at the cell centers.

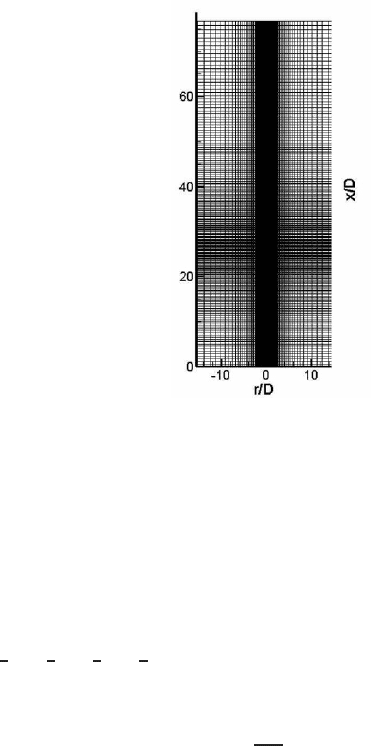
constructed with hyperbolic sine and tangent functions to cluster the majority of

grid points in the high-strain region of the jet. A typical distribution of the grid

is shown in Figure 5. The circular fuel nozzle surrounded by an annulus of pilot

278

Large Eddy Simulation of Jet Flames

Fig. 5 A typical non-uniform grid used for the combustion simulations.

mixture and an annulus of air are located in the y −z plane at x = 0. Simulations

were performed on a 200× 96×96 (X×Y×Z) grid with in x and y direction ap-

proximately 40 points in the nozzle region to resolve the strong jet shear-layers.

The dimensions of the computational domain are 70×30×30 nozzle diameters.

For the calculation of the derivative of a certain variable f on the non-uniform

grid we map f on a corresponding uniform grid. The ﬁrst-order derivative is al-

ways calculated on the uniform grid. When a variable is known on the cell faces,



...,i −

,i −

,i +

,...



the following formula is used to ﬁnd the derivative

at the center of the cell, [...,i −1, i,i + 1, ...]:

′

+ a



′

i+1

+ f

′

i−1



∑

n=1

∆



i+(2n−1)/2

− f

i−(2n−1)/2



. (30)

Thus, the variable is implicitly swapped from the cell face to the cell center. In

equation (30) f

′

is the derivative of a certain variable f with respect X, i.e. d f /dX in

grid point i.

∆

X is the uniform grid point distance. The coefﬁcients a

can be found

with Taylor expansions around grid point i. Having the coefﬁcients a

,..,a

it is

theoretically possible to achieve tenth-order accuracy, but close to the boundary the

stencil is made smaller, since one-sided differences are applied there. Interpolation

is carried out with the following formula:

+ b

( f

i+1

+ f

i−1

) =

∑

n=1



i+(2n−1)/2

+ f

i−(2n−1)/2



. (31)

279

S. van der Hoeven, B.J. Boersma, and D.J.E.M. Roekaerts

n 0 1 2 3 4

49/190 12985/14592 78841/364800 -343/72960 129/851200

7/18 1225/1536 49/512 -7/1536 1/4608

Table 1 Coefﬁcients for the derivative and interpolation rule with a tenth-order stencil.

5 Boundary conditions

Since the developed code is low-dissipative, (acoustic) waves can reﬂect at the do-

main boundaries and disturb the ﬂow. Therefore special attention must be paid to

the treatment of the boundaries. Different boundary condition methods were imple-

mented and tested. The class of methods using characteristic boundary conditions

is attractive since it allows to control the behavior of characteristic waves in a di-

rect way. We have implemented the Navier-Stokes Characteristic Boundary Condi-

tions (NSCBC) method of Poinsot and Lele [9] in our staggered grid arrangement.

The NSCBC method works well for combustion simulations where acoustics are

unimportant, but for a staggered grid it appeared to be computationally expensive to

deﬁne all necessary quantities locally at the cell faces. This holds especially for sub-

sonic outﬂow conditions. Another drawback of (linearized) characteristic BC’s such

as the NSCBC method is that it is very difﬁcult to convect a hot jet ﬂow out of the

domain without using artiﬁcial sponge layers. This is due to the multi-dimensional

nature of the structures in jet ﬂows for which a simple pressure relaxation method

is not good enough. Yoo et. al. [10] proposed to solve the problem by extending the

NSCBC method with multi-dimensional corrections.

We follow another procedure which is a variant of the methods proposed by Colo-

nius et. al. [11], Ta’asan et. al. [12] and Berenger [13]. This method was applied by

Freund [14] in aeroacoustics simulations. In this procedure the computational do-

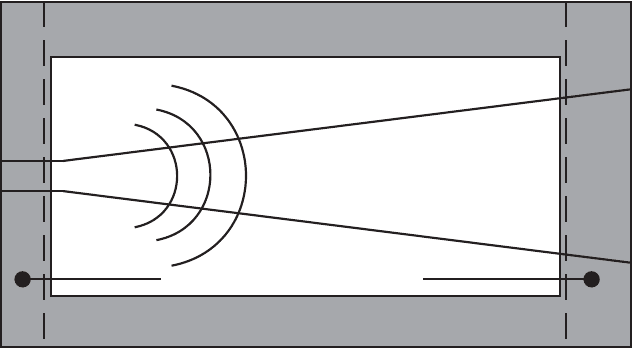
main contains a non-physical boundary region where extra boundary terms appear

in the governing transport equations (Fig. 6). This non-physical region uses nearly

one percent of the total amount of grid points. Several approaches can be followed

within this boundary domain, and we have combined two of them. The ﬁrst is to

force the solution towards some target solution, by adding a term

(

−

target

) to

the transport equation for

∂φ

∂

= RHS +

(

−

target

), (32)

where

is a conserved quantity, RHS stands for all terms of the unforced equation

and

is a forcing parameter being nonzero only in the artiﬁcial boundary layer.

target

can be a time-averaged value or a known solution, e.g. from a RANS cal-

culation [15]. The second approach is to add a term which gives disturbances an

increased convection velocity according to a given proﬁle which is supersonic in

the unphysical region and decreases to zero at the interface between unphysical and

physical region. The latter terms prevent that at the in- and outlet boundaries reﬂec-

tions travel backwards into the domain. This is done in the following way:

∂φ

∂

= RHS −U

∂φ

∂

, (33)

280

Large Eddy Simulation of Jet Flames

where U

is the given velocity proﬁle, being nonzero only near the inlet and out-

let plane. At the lateral boundaries we prescribed a simple reﬂecting characteristic

boundary condition with ﬁxed velocities. Although such a boundary condition al-

lows waves to reﬂect, any disturbance is damped by forcing the solution to the time-

averaged solution as proposed in eq. (32).

Artificial boundary region (σ≠0)

Physical domain (σ=0)

Inlet boundary

Supersonic convection layer

Acoustic radiation

Outlet boundary

Fig. 6 Schematic view of computational domain with artiﬁcial boundary layer.

In order to minimize non-physical behavior at the walls originating from 2

∆

x in-

stabilities we applied explicit ﬁltering every 25 time steps in the artiﬁcial bound-

ary region. At each boundary of the computational domain, only the component of

velocity orthogonal to that boundary is ﬁltered. (We recall that the computational

domain is a rectangular box.) We have used a ﬁlter of the form:

n−3

−6

n−2

+ 15

n−1

+ 44

+ 15

n+1

−6

n+2

n+3

, (34)

which ﬁlters 2

∆

x waves from the solution. In the vicinity of the walls the ﬁlter

stencil is adjusted to one-sided differences.

5.1 Parallel implementation

The model described above has been implemented in Fortran77/Fortran90 and par-

allelized with the message passing interface MPI. The parallel implementation of

the model will be described in this section.

The total calculation consists of N

×N

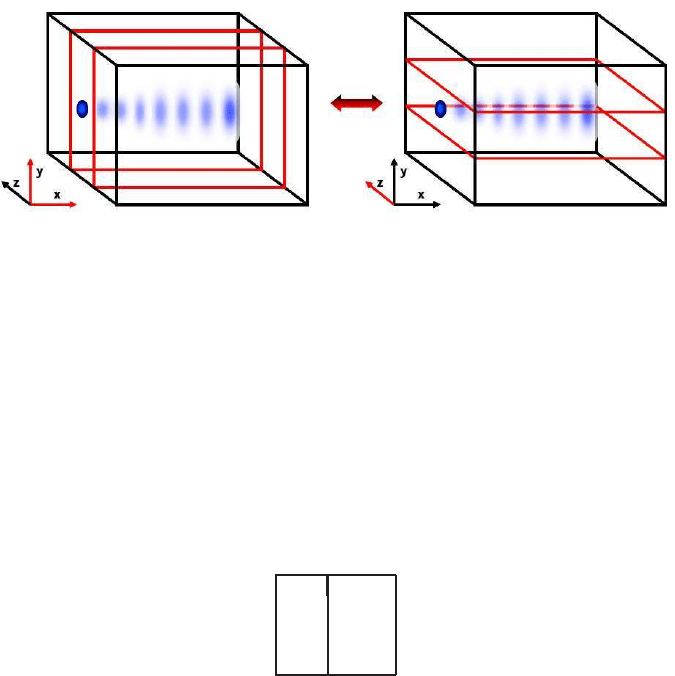
grid points. We use two data distri-

butions, one with N

×N

×(N

)/P points, where P is the number of processors and

one with N

×(N

)/P ×N

, see Figure 7. On the ﬁrst distribution we can calculate

281

S. van der Hoeven, B.J. Boersma, and D.J.E.M. Roekaerts

all the derivatives in the x and y direction. On this distribution only a part of the z

direction is available and we can not calculate the z derivatives. For the z deriva-

tives we use the second data distribution. The z derivatives are communicated to the

ﬁrst distribution and the Runge-Kutta (sub)steps on the ﬁrst distribution. After the

Runge-Kutta (sub)step all values are communicated to the second data distribution

and a new (sub)step can be performed.

Fig. 7 The decomposition of the computational domain in a distribution with N

×N

×(N

)/P

and with N

×(N

)/P ×N

points.

All the communication is performed with the MPI routine MPIALLTOALL. Due

to the implicit nature of the compact differences we need all points in a speciﬁc

direction to be present on a single CPU and we can not use nearest neighbor com-

munications as is used in standard ﬁnite difference codes.

Due to global nature of the communication our model only works on parallel

computers with very efﬁcient communication hardware. The model will run on a Be-

owulf cluster but it will be slow. On modern supercomputers, like the IBM-SP5/SP6

the model works well up to a large number of CPUs as can be seen from table 1.

Table 2 Times of the numerical model obtained on an IBM-SP5

# CPU time/step

2 34 sec

4 21 sec

8 13 sec

16 7 sec

6 Simulation details

Laminar inﬂow conditions were prescribed at the inlet section. Since the ﬂow is

locally supersonic we may prescribe all variables:

, eu, ev, ew,

E and

Z. The axial ve-

282

Large Eddy Simulation of Jet Flames

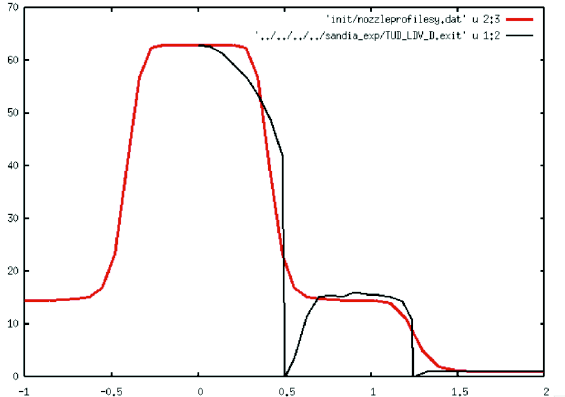
locity and mixture fraction proﬁles were taken from experimental data [6] and re-

constructed with polynomial approximations. The inﬂow proﬁle in the experiment

has very large gradients, see Figure 8, and these large gradients could not be re-

constructed with the present fairly course grid resolution. The difference between

inﬂow proﬁles in the simulations and experiments will remain visible throughout

the whole simulation.

Fig. 8 The inﬂow proﬁle from the SANDIA experiment and our polynomial ﬁt.

The ﬂame simulations are performed by starting with a cold ﬂow simulation. After

the cold jet has developed completely the ﬂamelet relaxation term as speciﬁed in

Equation (22) is added to the energy equation. With this approach the temperature

in the LES model approaches the ﬂamelet temperature as can be seen from Figure

In ﬁgure 10 we show contour plots of the Favre-averaged velocity, the eddy vis-

cosity and the Favre-averaged temperature. The region outside the black box is the

non-physical region where additional terms to handle boundary conditions have

been added. In Figure 11 we compare the predicted radial proﬁles of time aver-

aged resolved axial velocity and the variance of the axial velocity ﬂuctuations, with

the experimental data. Overall the agreement between the simulations and experi-

ments is reasonable. The difference between experiment and simulation can be due

to several reasons. The main reason is probably the difference in the inﬂow pro-

ﬁles as shown in Figure 8, and the fact that laminar inﬂow proﬁles were assumed in

the simulations. The predicted time averaged resolved temperature proﬁles and the

standard deviation of temperature are compared with experimental results in Fig-

ure 12. Again we observe a reasonable agreement. The agreement is not as good as

what has been obtained using a RANS model [20, 21] but comparable to earlier low

283