Комаров Ю.Ю. Проектирование и изготовление аэрокосмических аппаратов

Подождите немного. Документ загружается.

Этому вопросу должна быть посвящена отдельная работа, которая пла-

нируется для следующих НИРС.

Библиографический список

1. Жуковский Н. Е. Полное собрание сочинений. Т. III. – М. 1937.

2. Полухин Д. А. и др. Отработка ПГС двигательных установок ракет-носителей и

космических аппаратов с ЖРД. – М.: Машиностроение, 1978.

3. Machine Design. v.22. №3. 1950. P. 114-116.

4. Продольные колебания ракет на жидком топливе (обзор) // Вопросы ракетной тех-

ники. 1971. №11.

5. Raumfahrschung, Helf. 1/1972, S. 15-21.

6. Исследование взаимосвязи продольных и изгибных колебаний ракет “Сатурн-5”

активном участке полета // ВРТ. 1971. №4.

7. Гидравлический стендовый демпфер. Комплект документов ОАО “Энергомаш”. На

правах рукописи.

8. Черток Б. Е. Ракеты и люди. Фили-Подлипки-Тюратам. – М.: Машиностроение,

1996.

9. Исследование динамики объектов РКТ на земле – гарантия и работоспособность в

полете // ФППК. 2002. №6.

10. Седов Л. И. Размышления о науке и об ученых. – М.: Наука, 1980.

11. Федосеев И. Е., Хомяков А. М. Гидродинамический способ демпфирования коле-

баний в жидкостных магистралях ЖРД. В сборнике трудов // Проектирование, кон-

струирование и производство авиационной техники / Под ред. Ю. Ю. Комарова. –

М.: Изд-во МАИ, 2005.

Л. В. Гуров, А. М. Хомяков

Московский авиационный институт (государственный технический университет)

НОВЫЙ СПОСОБ УПРАВЛЕНИЯ ВЕКТОРОМ ТЯГИ

ЛЕТАТЕЛЬНОГО АППАРАТА

Для управления полётом ЛА рационально использовать энергию основ-

ных двигателей (основного двигателя). Применение автономной системы

управления ведёт к увеличению массы двигателя и общего числа агрега-

тов, что снижает манёвренность ЛА и его надёжность. Поэтому энергия

современных ЖРД непосредственно используется для управления полётом.

Например, ЖРД снабжаются узлами качания. Камеры при этом совершают

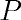
возвратно-поворотные движения – качания. В этом случае вектор тяги так-

же совершает угловые смещения; его проекция на ось, перпендикулярную

оси симметрии ЛА, создаёт усилия, используемые для управления ЛА. Это

усилие называют управляющим —

Способ качания двигателя или его камеры необходимо учитывать при

проектировании компоновки двигателя и ЛА. В этом случае, помимо ком-

поновочной, должна быть решена кинематическая задача, состоящая из

следующих двух частей:

1) исполнительный орган (двигатель, камера или её часть, ИО) должен

иметь кинематическую возможность принимать определённые положения

в пространстве двигателя;

2) исполнительный орган при своём угловом смещении не должен вы-

ходить за габариты ЛА.

Кинематическая возможность ИО в ЖРД достигается тем, что трубо-

проводы и газоводы снабжаются подвижными или упругими элементами,

которые позволяют осуществить движение ИО в системе двигателя. Прак-

тическое применение в последнее время нашли упругие элементы в виде

мембран, диафрагм и сильфонов. Сам ИО может устанавливаться либо

на шарнирном, либо на кардановом подвесе. В первом случае управление

полётом осуществляется по одному каналу, во втором — по двум каналам

(тангаж и рыскание).

Ограничение угловых смещений ИО следует из того, что качающий узел

не должен выходить за габариты ЛА, с тем чтобы не создавать внешний

демпфирующий момент при взаимодействии ИО с воздушным потоком.

Это характерно для первых ступеней ракет-носителей. Для верхних сту-

пеней ограничение угла поворота может быть связано с пожарной опасно-

стью на ЛА.

C точки зрения компоновки двигателя, наиболее рациональными явля-

ются схемы, представленные на рис. 1, в которых узлы качания как тако-

вые отсутствуют. В случае применения этих схем отпадает ограничение

по угловым смещениям вектора тяги. Сама система управления по числу

агрегатов и узлов также оказывается более приемлемой. Необходимо ре-

шить вопрос об эффективности таких способов управления в современных

ЖРД.

С нашей точки зрения, более рациональной может оказаться схема G.

В этом случае нет необходимости применять дополнительно рабочее те-

ло (для вдува газа), управление полётом осуществляется путём отбора и

выхлопа продуктов сгорания из сопла во внешнюю среду.

Схема B, как и схема A, может обеспечивать управление полётом по

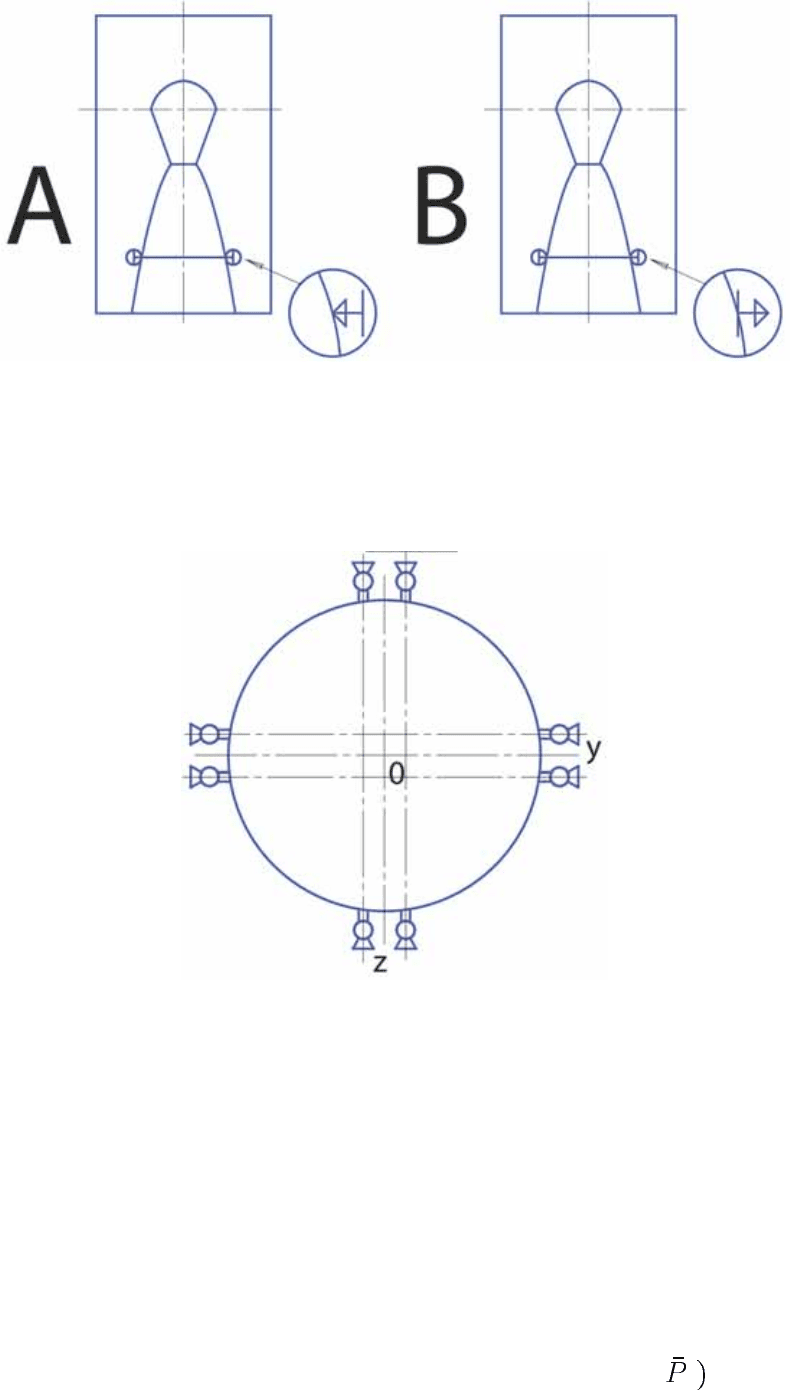
Рис. 1. Схемы исполнительных органов

системы управления вектором тяги ЛА

трем каналам (тангаж, рысканье и крен) при парной установке управляю-

щих сопл для каждого канала (рис. 2).

Рис. 2. Вариант размещения управляющих сопл,

позволяющих управление по крену ЛА

И схема B, уже в отличие от схемы своего основного конкурента –

схемы A, – позволяет спроектировать выносные органы управления или

комбинированные, позволяющие управлять ЛА как по угловым, так и по

линейным координатам (рис. 3).

Необходимо при этом определить, насколько эффективна предложенная

нами гидравлическая схема для создания легкого (по массе) и надёжного

исполнительного органа СУВТ ЛА. Практически важно в нашем случае

найти способ определения достаточно точных значений коэффициента эф-

фективности (К) и относительного управляющего усилия (

Решение задачи по определению эффективности управляющего сопла,

Рис. 3. Варианты размещения управляющих сопл на ЛА

работающего на отборе части потока продуктов сгорания компонентов в

раструбе основного сопла, сводится, в свою очередь, к решению двух под-

задач:

1) определение структуры потока в основном сопле при открытии кла-

пана управляющего сопла и получение значений параметров газа перед

последним (в зависимости от площади проходного сечения клапана, свя-

занной со значением угла поворота кулачка, который в нашей задаче тож-

дественен углу поворота ИО

– задача I;

2) вывод расчётной зависимости для тяги управляющего сопла – зада-

ча II.

Задачей I является определение параметров газового потока в основном

сопле при открытии клапана в боковом управляющем сопле. Для реше-

ния этой задачи нами была использована одна из программ структурного

анализа (CosmosFloWorks). Расчётная схема, принятая для решения пред-

ставляет собой участок цилиндрической трубы длиной

, соответствую-

щий раструбу основного сопла, с цилиндрическим отводом (окном), ось

симметрии которого перпендикулярна оси трубы (рис. 4)

Граничные условия в такой схеме, т.е. значения параметров газового

потока в трёх сечениях цилиндрической трубы и отвода, принимались с

учётом расчёта параметров потока в основном сопле по газодинамическим

функциям:

Полученные при этом значения параметров в окрестности бокового от-

верстия являются исходными данными для решения задачи II. Решение

задачи I показывает (рис. 5), что заметной асимметрии на срезе сопла не

наблюдается. Это означает, что дополнительный момент на основном соп-

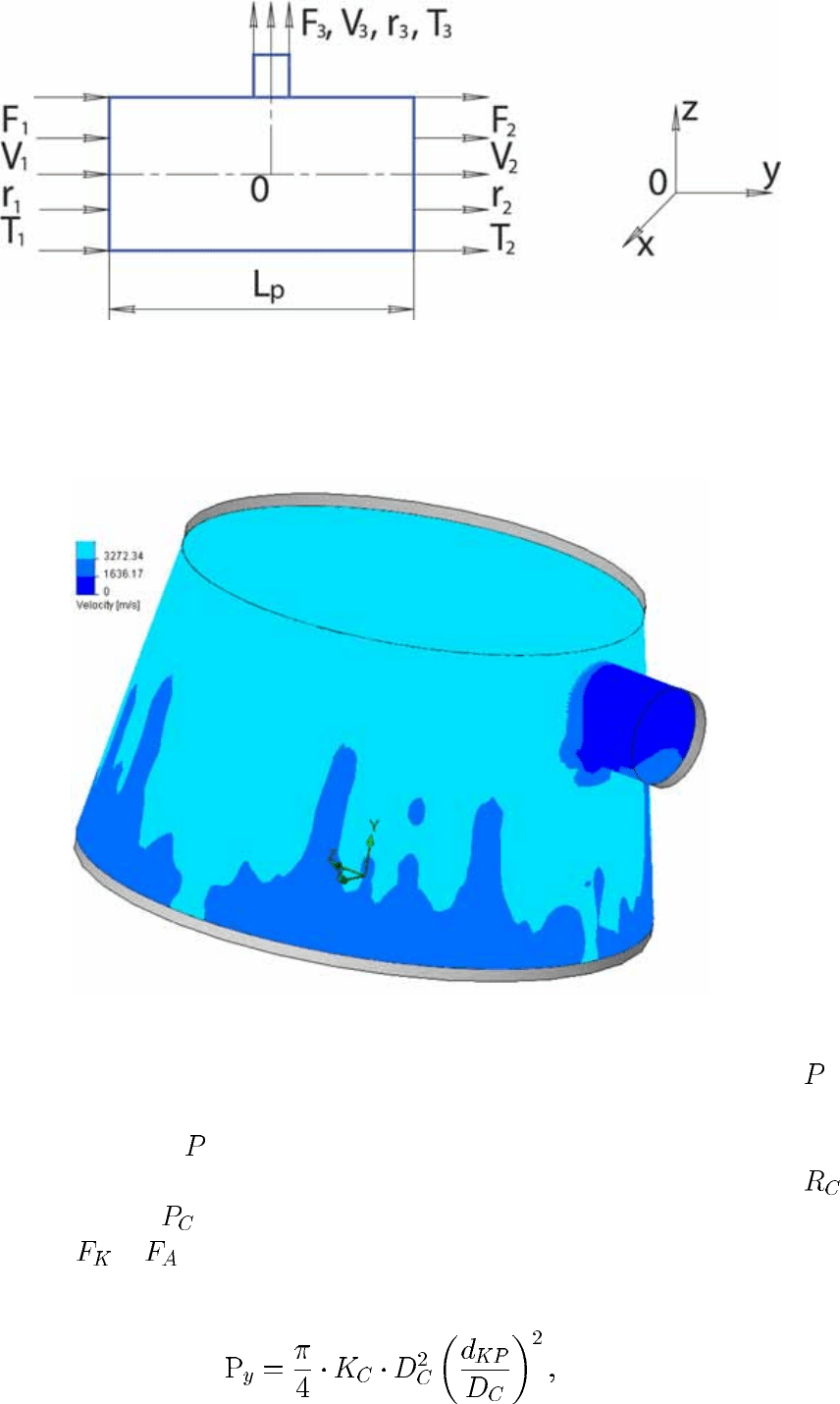
Рис. 4. Расчётная схема

ле при открытии бокового управляющего сопла не возникает. Последнее

обстоятельство требует дополнительного изучения.

Рис. 5. Распределение скоростей газа по объёму сопла с отверстием

Задачей II является определение значения управляющего усилия

которое возникает при открытии бокового сопла.

Расчёт величины

основывается на том, что основное сопло в сечении

управляющего сопла представляет собой замкнутую камеру с размером

и давлением газа , снабжённую соплом с характерными поперечными

сечениями

и (рис. 6).

В качестве расчётной зависимости принимается равенство

(1)

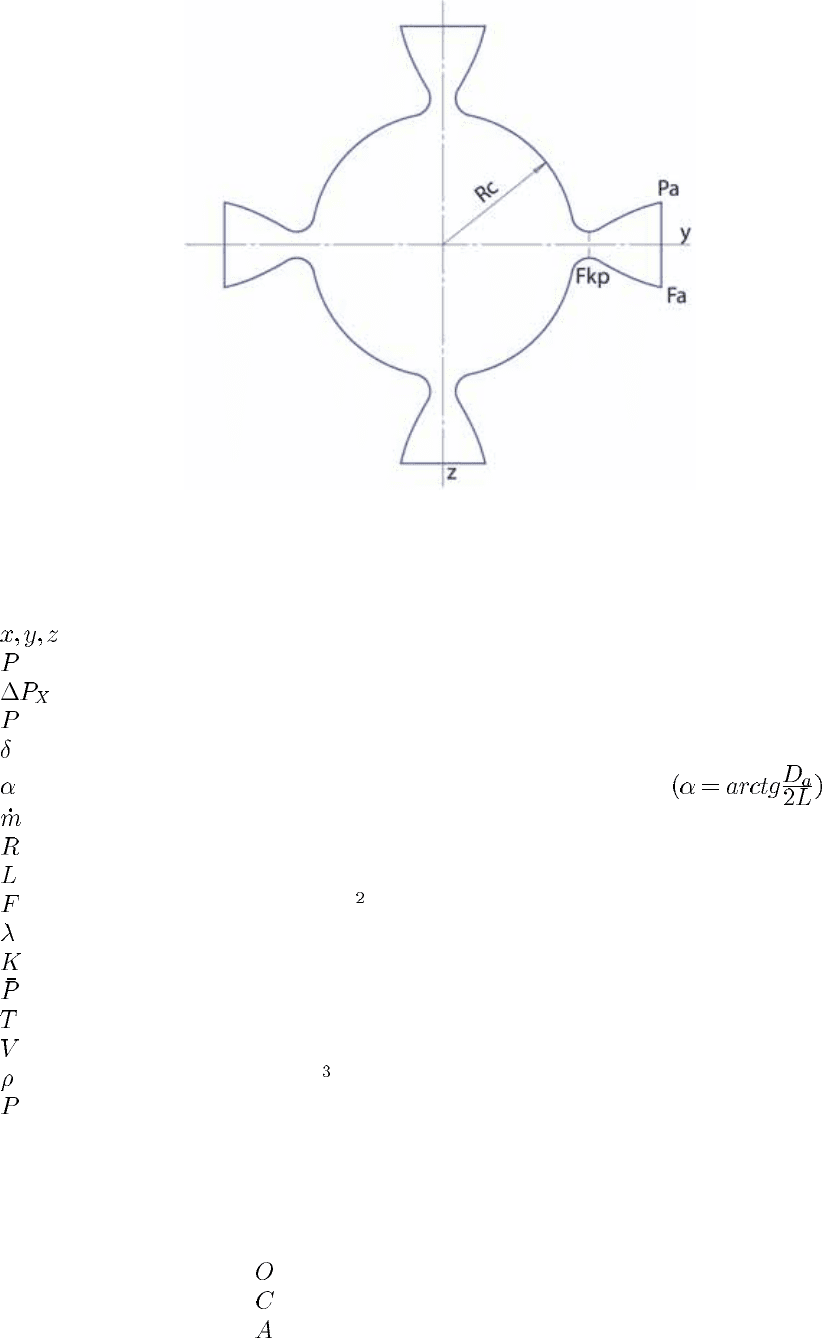
Рис. 6. Расчётная схема

Обозначения:

— декартова система координат;

— тяга двигателя, H;

— потеря осевой тяги двигателя, H;

— управляющая сила, H;

— угол поворота исполнительного органа, рад;

— характерный угол в кинематической схеме узла качания , рад;

— секундный расход газа, кг/с;

— радиус, м;

— длина, м;

— площадь сечения сопла, м ;

— безразмерная скорость потока;

— коэффициент эффективности;

— относительное управляющее усилие;

— температура газа, K;

— скорости потока, м/с;

— плотность потока, кг/м ;

— давление, Па.

Индексы:

– основное сопло;

– боковое (управляющее) сопло;

– срез сопла;

где .

Безразмерная скорость на срезе управляющего сопла

рассчитывается

с использованием газодинамической функции

(2)

Исходные данные для расчётов

МПа – варианты значений статического давления в основ-

ном сопле в сечении расположения боковых управляющих сопел;

м – диаметр сечения основного сопла;

– геометрическое соотношение;

– показатель адиабаты;

МН – тяга двигателя.

Предлагаемый способ выдува (отбора) газов из сопла уступает вдуву

газов в основных характеристиках. Наши расчёты показывают, что коэф-

фициент эффективности выдува приближается к единице, а относительное

управляющее усилие (

у у

составляет несколько процентов.

Таким образом, в реальном проекте двигателяивотношении нашего

способа вопрос применения будет рассматриваться на основе разрешения

главного проектного противоречия между компоновкой и массой двигателя

и эффективностью управления вектором тяги.

Библиографический список

1. Пичугин Д. Ф. Конструкция и проектирование агрегатов двигателей летательных

аппаратов: Учебное пособие. – Куйбышев, КуАИ, 1989.

2. Хомяков А. М. Конструкция и проектирование ДЛА: Учебное пособие. – М.: Изд-во

МАИ, 1989.

3. Сварич К. М., Хомяков А. М. Элементы теории компоновочного проектирова-

ния. Проблемы перспективной авиационной техники // Сборник статей научно-

исследовательских работ студентов, аспирантов и молодых учёных. – М.: Изд-во

МАИ, 1999.

4. Алямовский А. А. SolidWorks/COSMOSWorks. Инженерный анализ методом конеч-

ных элементов. ДМК Пресс, 2004.

5. СOSMOSFloWorks Tutorial, COSMOS Analysis Products, 2006.

К. А. Иванов, А. И. Федюшкин, А. А. Пунтус

Московский авиационный институт (государственный технический университет)

КРАТКИЙ ОБЗОР ПУБЛИКАЦИЙ ПО ИССЛЕДОВАНИЮ

ОБТЕКАНИЯ ТВЁРДОГО ШАРА ПРИ МАЛЫХ ЧИСЛАХ

РЕЙНОЛЬДСА

Данная статья представляет собой обзор результатов исследований за-

дачи обтекания твердого шара при малых числах Рейнольдса, нашедших

отражение в учебной литературе.

В качестве вступления процитируем [2]: «... до сих пор целый ряд мето-

дов малого параметра, особенно применительно к нелинейным уравнениям

в частных производных, нельзя считать строго обоснованными, и успех их

применения часто бывает связан с глубоким и неформальным проникно-

вением в суть задачи, с пониманием процессов, описываемых данными

уравнениями. В настоящее время, в эпоху быстрого развития вычисли-

тельной техники, методы малого параметра отнюдь не утрачивают своего

значения. Они служат для выяснения качественных особенностей задач,

для получения асимптотик и анализа особых точек, для построения опор-

ных “тестовых” решений, а в ряде случаев являются также основой для

разработки вычислительных методов».

Движение несжимаемой жидкости будем называть стационарным

(установившимся), если векторное поле скоростей не зависит явным об-

разом от времени. В противном случае движение несжимаемой жидкости

называется нестационарным (неустановившимся).

Установившиеся движение жидкости

Рассмотрим прямолинейное и равномерное движение шара в вязкой

жидкости. Эта задача вполне эквивалентна задаче об обтекании неподвиж-

ного шара потоком жидкости, имеющим на бесконечности заданную ско-

рость

. Распределение скоростей в первой задаче получается из решения

второй задачи просто вычитанием скорости

; тогда жидкость на бесконеч-

ности оказывается неподвижной, а шар движется со скоростью -

. Если

мы рассматриваем движение как стационарное, то надо, конечно, говорить

именно об обтекании жидкостью неподвижного шара, так как при движу-

щемся шаре скорость жидкости в каждой точке пространства меняется со

временем. Итак, шар неподвижен. Система координат показана на рис. 1.

Вычисления произведены здесь не в терминах скорости

,ав

менее наглядных, но более компактных терминах функции тока. Для осе-

симметричных течений (к которым относится обтекание шара) функция

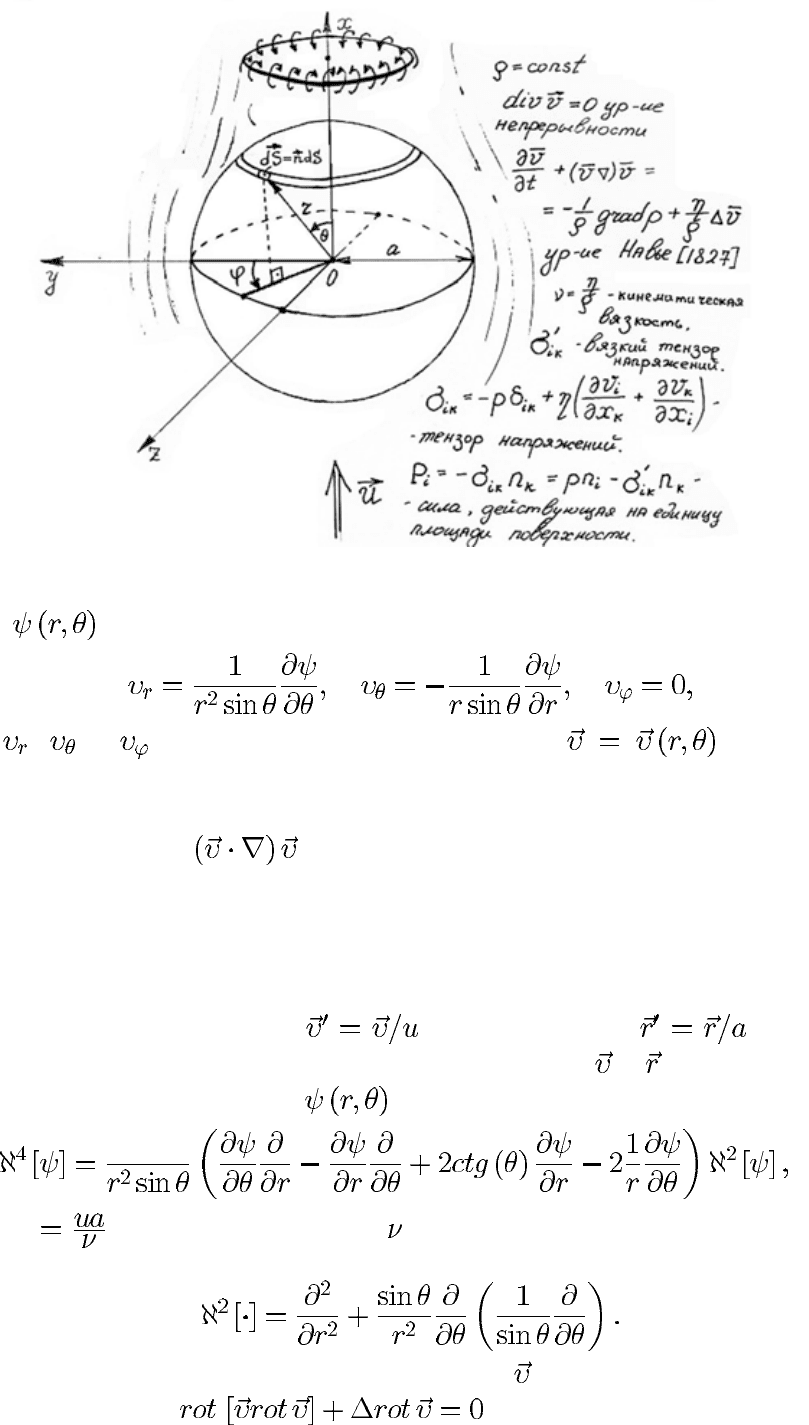
Рис. 1. Введение системы координат

тока в сферических координатах, вводится согласно определению

где , и - компоненты вектора скорости в сфериче-

ской системе координат. Тем самым тождественно удовлетворяется урав-

нение непрерывности. Полная система уравнений Навье—Стокса (с учётом

нелинейного члена

и термодинамической необратимости процес-

са, связанной с наличием внутреннего трения (вязкости) ) в сферической

системе координат задаёт следующее безразмерное уравнение (так как в

дальнейшем будем использовать метод возмущения по малому параметру,

то для явного выявления малого параметра Re - числа Рейнольдса - вве-

дём безразмерные скорость

и радиус-вектор и ниже в

этом пункте будем обозначать их теми же буквами

и , опуская штрих)

относительно функции тока

(1)

где Re

— число Рейнольдса ( - кинематическая вязкость) и исполь-

зован оператор

Стоит заметить, что в терминах скорости уравнение (1) имеет более

наглядный вид Re

(1’).

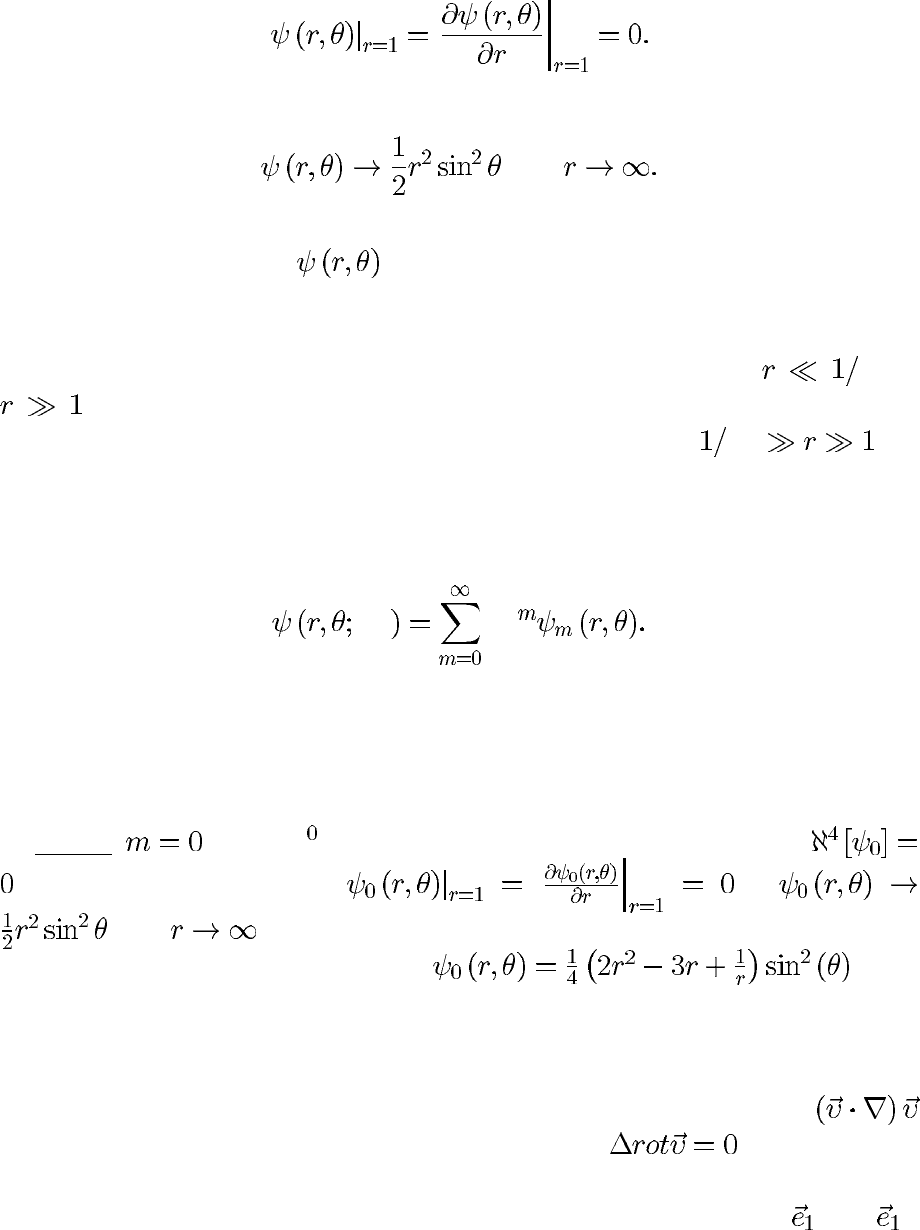
Граничные условия на поверхности сферы требуют обращения в ноль

скорости; в безразмерном виде для функции тока будем иметь

(2)

Из условия равномерности потока на бесконечности имеем

при (3)

Соотношения (1)-(3) определяют корректно поставленную задачу отно-

сительно функции тока

В [1], для удобства физического осмысления, предложено выделить в

пространстве вокруг неподвижного обтекаемого шара две области: ближ-

нюю и дальнюю, определённые соответственно условиями

Re и

. Вместе эти области исчерпывают всё пространство, причём ча-

стично они перекрываются в “промежуточной” области

Re .

Идея состоит в том, чтобы искать формальное разложение типа Пуан-

каре, справедливое при малых числах Рейнольдса Re (т.е. при медленных

течениях жидкости):

Re Re (4)

Согласно [2, с. 39-41], подставляя (4) с учётом условия (3) в уравнение (1),

раскладывая при малом Re и приравнивая коэффициенты при одинаковых

степенях Re, получим (пропуская все необходимые вычисления) следую-

щие результаты:

Шаг 1

. . При Re : Требуется решить следующую задачу:

, с краевыми условиями

при .

Решением этой задачи является

.В[2

с. 40] оно получено методом разделения переменных. Это решение, полу-

ченное Стоксом (1851), является исходным приближением в ближайшей

области. Тот же результат может быть получен если в (1) пренебречь чле-

ном с множителем Re (т.е. мы пренебрегаем нелинейным членом

в уравнении Навье (1827)), т.е. решать уравнение с соответству-

ющими краевыми условиями (в безразмерном виде на поверхности шара

скорость обращается в ноль, а на бесконечности она постоянна ,где -

единичный вектор вдоль оси абсцисс (направления обтекания) (см. рис. 1)).

Этот второй путь мне кажется более тяжёлым (по меньшей мере он тре-

бует знания некоторых элементов теории поля), но не менее интересным.