Колесников А.А. Синергетические методы управления сложными системами: энергетические системы
Подождите немного. Документ загружается.


dδ
dt
= s;
Tj
ds
dt
= P
T
− E
2
y
11
sin α
11
− EU
c
y
12
sin(δ −α
12
)+F (t);
T
d0
dE
dt
= −E + U
c
y
12
T
d0
(x
d
− x
d
)s sin(δ − α
12
)+U
1
;
T
c
dP
T
dt
= −P
T
−
s
σ
+ U
2
,
δ s E
P
T
U
1
U
2
F (t)
ω
0
y
11
y
12
α
11
α
12
x
d
,x
d
T
d0
T
c
Tj
U
c
σ
x
1
= δ x
2
= s x
3
= E x
4
= P
T
a
1
= y
11
sin α
11
a
2
= U
c
y
12
a
3
= T
d0
(x
d
− x
d
)U
c
y
12
a
4
=1/σ b
1
=1/T j b
2
=1/T
d0
b
3
=1/T
c
dx
1
dt
= x
2
;
dx
2
dt
= b
1
(x
4
− a
1
x
2
3
− a
2
x
3
sin(x
1
− α
12
)+F (t));
dx
3
dt
= b
2
(−x
3
+ a
3
x
2
sin(x
1
− α
12
)+U
1
);
dx
4
dt
= b
3
(−x
4
− a
4
x
2
+ U
2
).
U
1
U
2
F (t)=0
x
3
− x
0
3
=0,

x
0
3
x
4
= x
0
4
= const
x
0
4
− a
1
(x
0
3
)
2
− a
2
x
0
3
sin(x
0
1
− α
12
)=0;
U = U
0
= const
U
2
0
− U
2
= U
2
0
− A(x
0
3
)
2
− 2Bx
0
3
− D =0,
A =1− 2y
11
x
d
cos α
11
+(y
11
x
d
)
2
B = U
c
y
11
x
d
(cos(x
0
1
− α
12
) − y
11
x
d
cos(x
0
1
− α
12
+ α
11
))
D =(U
c
y
12
x
d
)
2
x
1
− x
0
1
=0,
x
0
1
ψ
1
= b
11
(x
3
− x
0
3
)+b
12
(x
4
+ ϕ
1
),
ψ
2
= b
21
(x
3
− x
0
3
)+b
22
(x
4
+ ϕ
1
),
ϕ
1
T
1
˙
ψ
1
(t)+ψ
1
=0,
T
2
˙
ψ
2
(t)+ψ
2
=0.
ψ
1
=0
ψ
2
=0
dx
1ψ
dt
= x
2ψ
,
dx
2ψ
dt
= b
1
(−ϕ
1
− a
1
(x
0
3
)
2
− a
2
x
0
3
sin(x
1ψ
− α
12
)).
ϕ
1
ϕ
1
ψ
3
= x
2
+ γ(x
1
− x
0
1
),
γ

ψ
3
=0
T
3
˙
ψ
3
(t)+ψ
3
=0.
ϕ
1
= −a
1
(x
0
3
)
2
− a
2
x
0
3
sin(x
1
− α
12
)+
'
x
2
(T
3
γ +1)+γ(x
1
− x
0
1
)
(
/(T
3
b
1
).
ψ
3
=0
dx
1ψ
3
dt
= −γ(x
1ψ
3
− x
0
1
),
γ>0
U
1
= k
0
x
3
+ k
1
(x
3
− x
0
3
)+k
2
x
4
+ k
4
(x
1
− x
0
1
)+k
5
x
2
+(k
6
x
2
− k
7
)sin(x
1
− α
12
) − k
8
,
U
2
= k
9
x
4
+ k
10
x
2
3
− k
11
(x
3
− x
0
3
) − k
16
(x
1
− x
0
1
)+(k
12
x
3
+ k
13
)sin(x
1
− α
12
)+k
17
x
2
+
+ k
18
x
2
cos(x
1
− α
12
)+k
19
,
p
0
= b
11
b
22
− b
12
b
21
p
1
=1/(p
0
b
2
) p
2
= b
12
b
22
/T
2
− b
11
b
22
/T
1
p
3
= b
12
b
22
(1/T
2
− 1/T
1
)
p
4
= γ/(b
1
T
3
) p
5
= p
4
(T
3
γ +1)/T
3
p
6
= γ/(b
3
T
3
) p
7
= p
6
(T
3
γ +1)/T
3
p
8
= b
11
b
22
/T
2
−b
12
b
21
/T
1
p
9
=1/(p
0
b
3
) p
10
=1−p
7
−p
8
p
9
p
11
= b
11
b
21
(1/T
2
−1/T
1
) p
12
= p
6
/(p
0
b
1
) p
13
= a
4
−p
7
p
8
p
9
/b
1
−
p
0
p
12
k
0
= p
0
k
1
= p
1
p
2
k
2
= p
1
p
3
k
4
= k
1
p
4
k
5
= k
2
p
5
k
6
= −p
0
a
3
k
7
= −k
2
a
3
k
8
= k
2
(x
0
3
)
2
k
9
= p
10
k
10
= a
1
p
7
k
11
= p
9
p
11
k
12
= a
2
p
7
k
13
= p
8
p
9
a
2
x
0
3
k
16
= p
8
p
12
k
17
= p
13
k
18
= a
2
x
0
3
/b
3
k
19
= a
1
p
8
p
9
T
1
,T
2
,T
3
,γ >0,b
12
b
21
= b
11
b
22
.
dx
1ψ
dt
= x
2ψ
,
dx
2ψ
dt
= −
γ
T
3
(x
1ψ
− x
0
1
) −
T
3
γ +1
T
3
x
2ψ
.
T
2
¨x
1ψ
(t)+2dT ˙x
1ψ
(t)+x
1ψ
(t)=x
0
1
,
T =
T
3
/γ d =(T
3
γ +1)/(2Tγ)

Tj =9,17 T
c
=4 T
d0
=6 σ =0,05 x
d
=2,5
x
d
=0,28 α
11
= α
12
=0,019 y
11
= y
12
=0,3 U
c
=1 ω
0
=1
T
1
= T
2
= T
3
=1 b
11
=2 b
12
= b
21
= b
22
=1 x
0
1
=1,695 x
0
3
=2,83 x
0
4
=0,85 γ =0,171
U
1min
= −1 U
1max
=3 U
2min
=0 U
2max
=1,1
x
1
(0) = 2π/3 x
2
(0) = −0,1 x
3
(0) = 1,2 x
4
(0) = 0,4
sat U
i
=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
U
imin
,U
i
U
imin
,
U
i
,U
imin
U
i
U
imax
,
U
imax
,U
i
U
imax
.
ψ
1
=0
ψ
2
=0
x
0
3
x
0
3
=2,67 x
0
4
x
1
(0) = 1,569 x
2
(0) = 0 x
3
(0) = 2,67 x
4
(0) = 0,85
E
qe
= k
0U
∆U + k
1U
∆U
dt
+ k
0f
∆ω + k
1f
∆ω
dt
,
∆U = U
0
−U U
0
∆ω =
ω − ω
0
k
0U
k
1U
k
0f
k
1f
µ
PT
= k
u
∆P
T
+
1
T
u
∆P
T
dt,
µ
PT
k
u
T
u
U
1
= E
qe
U
2
= µ
PT
k
0U
=50 k
1U
=7 k
0f
=30 k
1f
=8
k
u
=0,6 T
u
=2, 5
F (t)=A sin(Ωt)
F (t)
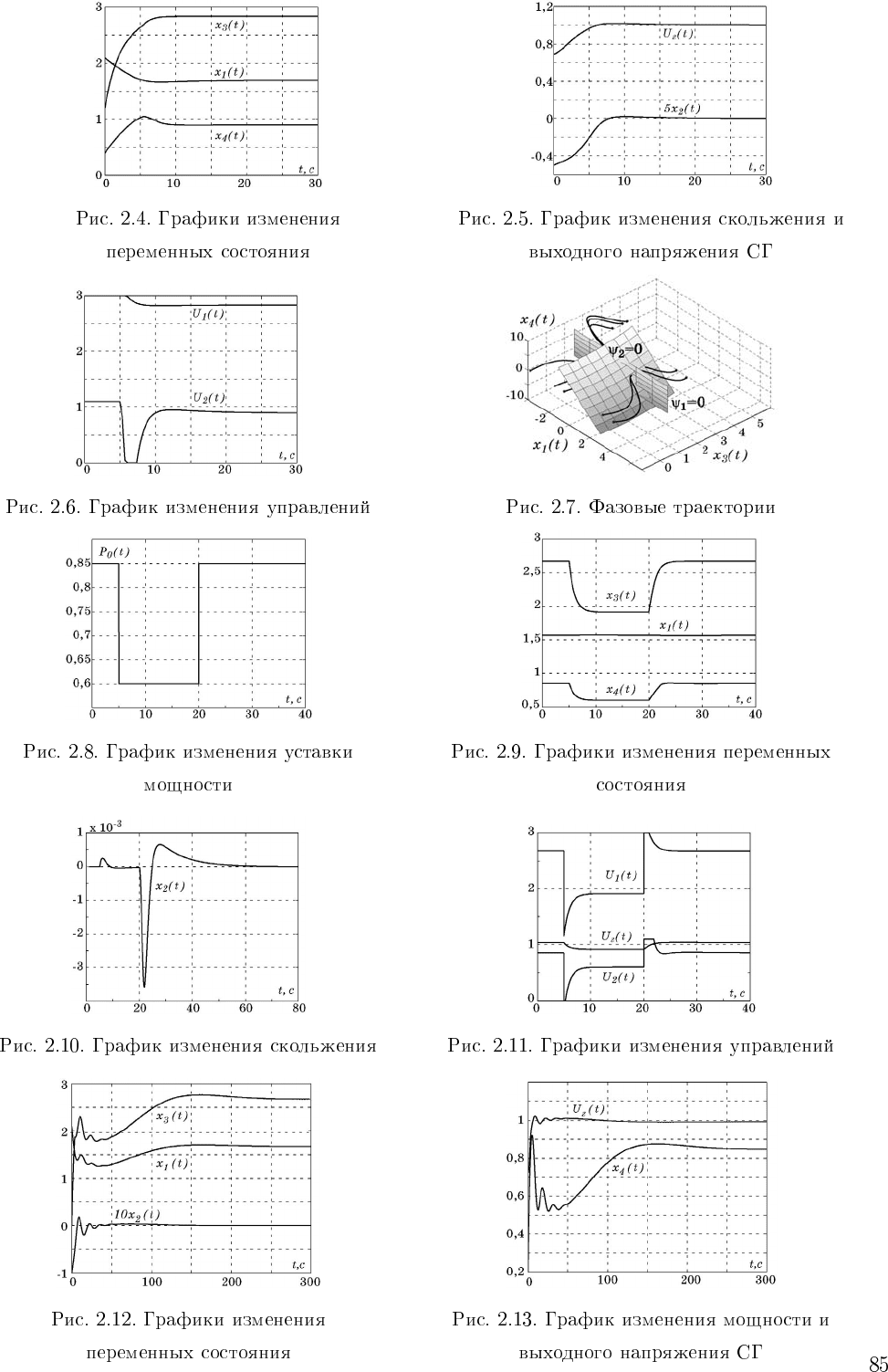

dw
1
dt
= w
2
,
dw
2
dt
= −Ω
2
w
1
,
F (t)=w
1
(t),
Ω
x
3
= x
0
3
x
1
= x
0
1
dx
1
dt
= x
2
;
dx
2
dt
= b
1
(x
4
− a
1
x
2
3
− a
2
x
3
sin(x
1
− α
12
)+c
1
x
5
);
dx
3
dt
= b
2
(−x
3
+ a
3
x
2
sin(x
1
− α
12
)+U
1
);
dx
4
dt
= b
3
(−x
4
− a
4
x
2
+ U
2
);
dx
5
dt
= x
6
;
dx
6
dt
= −Ω
2
x
5
,
x
5
= w
1
x
6
= w
2
c
1
ψ
1
= b
11
(x
3
− x
0
3
)+b
12
(x
4
+ ϕ
1
+ c
1
x
5
),
ψ
2
= b
21
(x
3
− x
0
3
)+b
22
(x
4
+ ϕ
1
+ c
1
x
5
),
ϕ
1
U
1
= U
∗
1
+ k
3
x
5
,
U
2
= U
∗
2
− k
14
x
5
− k
15
x
6
,
U
∗
1
U
∗
2
k
3
= c
1
k
2
k
14
= c
1
(p
7
+ p
8
p
9
) k
15
= c
1
p
9
p
0
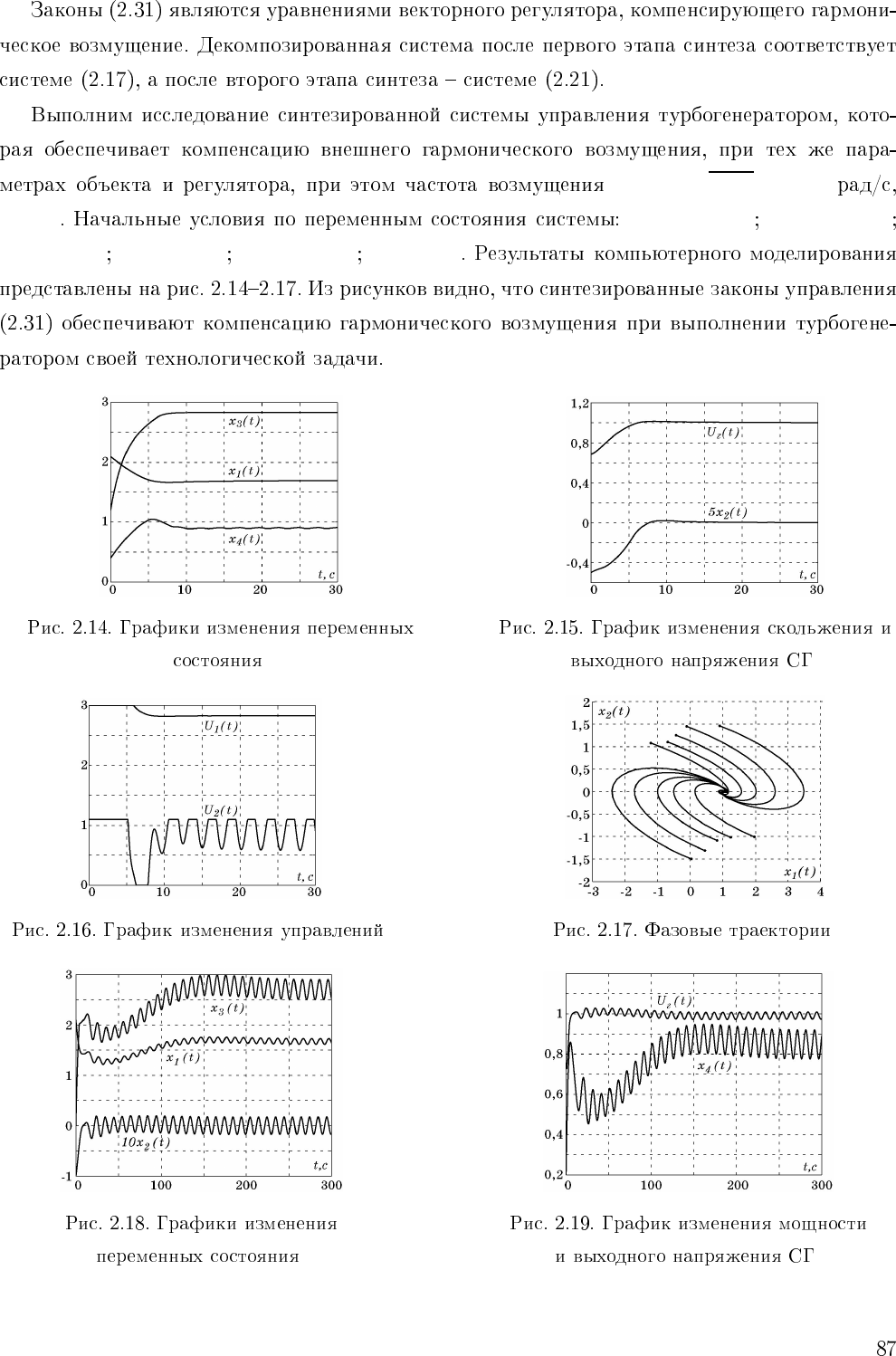
Ω=1/
T
3
/γ =0,41
c
1
=1 x
1
(0) = 2π/3 x
2
(0) = −0,1
x
3
(0) = 1,2 x
4
(0) = 0,4 x
5
(0) = 0,01 x
6
(0) = 0

U
1
= E
qe
U
2
= µ
PT
k
0U
=50 k
1U
=7 k
0f
=30 k
1f
=8
k
u
=0,6 T
u
=2, 5
•
•
•
F (t)=0
ψ
1
= b
11
(x
3
− x
0
3
− αx
2
)+b
12
(x
4
− x
0
4
+ η(x
1
− x
0
1
)+ξx
3
2
),
ψ
2
= b
21
(x
3
− x
0
3
− αx
2
)+b
22
(x
4
− x
0
4
+ η(x
1
− x
0
1
)+ξx
3
2
),
α η ξ
ψ
1
=0 ψ
2
=0
x
3
= x
0
3
+ αx
2
,x
4
= x
0
4
− η(x
1
− x
0
1
) − ξx
3
2
,
dx
1ψ
dt
= x
2ψ
,
dx
2ψ
dt
= b
1
(x
0
4
− η(x
1ψ
− x
0
1
) − ξx
3
2ψ
− a
1
(x
0
3
+ αx
2ψ
)
2
− a
2
(x
0
3
+ αx
2ψ
)sin(x
1ψ
− α
12
)).
α>0 η>0 ξ>0

U
1
= e
−1
1
(−T
1
b
22
b
12
+ b
22
b
12
T
2
+ T
2
b
1
b
21
αT
1
b
12
− T
2
b
1
αT
1
b
11
b
22
)x
4
+
+(b
22
b
12
ξT
2
− T
1
b
22
ξb
12
)x
3
2
+(−T
2
b
21
b
2
a
3
sin(x
1
− α
12
)T
1
b
12
−
− b
22
b
11
αT
2
+ T
2
b
2
a
3
sin(x
1
− α
12
)T
1
b
11
b
22
+ T
1
b
21
αb
12
)x
2
+
+(−T
2
b
1
b
21
αa
1
T
1
b
12
+ T
2
b
1
αa
1
T
1
b
11
b
22
)x
2
3
+(−T
2
b
2
T
1
b
11
b
22
−
− T
2
b
1
b
21
αa
2
sin(x
1
− α
12
)T
1
b
12
+ T
2
b
1
αa
2
sin(x
1
− α
12
)T
1
b
11
b
22
− T
1
b
21
b
12
+
+ b
22
b
11
T
2
+ T
2
b
21
b
2
T
1
b
12
)x
3
+(b
22
b
12
ηT
2
− T
1
b
22
ηb
12
)x
1
+ T
1
b
21
x
0
3
b
12
−
− b
22
b
11
x
0
3
T
2
+ T
1
b
22
ηx
0
1
b
12
− b
22
b
12
x
0
4
T
2
+ T
1
b
22
x
0
4
b
12
− b
22
b
12
ηx
0
1
T
2
,
U
2
= e
−1
2
((−3T
1
b
1
b
12
ξT
2
b
21
+3T
1
b
11
T
2
b
1
b
22
ξ)x
2
2
− b
12
T
2
b
21
+ T
1
b
12
b
3
T
2
b
21
−
− T
1
b
11
T
2
b
22
b
3
+ T
1
b
11
b
22
)x
4
+(−b
12
ξT
2
b
21
+ T
1
b
11
b
22
ξ)x
3
2
+ ((3T
1
b
1
b
12
ξa
1
T
2
b
21
−
− 3T
1
b
11
T
2
b
1
b
22
ξa
1
)x
2
3
+(−3T
1
b
11
T
2
b
1
b
22
ξa
2
sin(x
1
− α
12
)+
+3T
1
b
1
b
12
ξa
2
sin(x
1
− α
12
)T
2
b
21
)x
3
)x
2
2
+(T
1
b
11
T
2
b
22
η − T
1
b
11
b
21
α − T
1
b
11
T
2
b
22
b
3
a
4
−
− T
1
b
12
ηT
2
b
21
+ T
1
b
12
b
3
a
4
T
2
b
21
+ b
11
αT
2
b
21
)x
2
+(−b
11
T
2
b
21
+ T
1
b
11
b
21
)x
3
+
+(T
1
b
11
b
22
η − b
12
ηT
2
b
21
)x
1
+ b
11
x
0
3
T
2
b
21
− T
1
b
11
b
22
ηx
0
1
+ b
12
x
0
4
T
2
b
21
− T
1
b
11
b
21
x
0
3
+
+ b
12
ηx
0
1
T
2
b
21
− T
1
b
11
b
22
x
0
4
,
e
1
=(b
12
b
21
− b
11
b
22
)T
1
T
2
b
2
e
2
=(b
12
b
21
− b
11
b
22
)T
1
T
2
b
3
T
1
= T
2
=1 b
11
=2 b
12
= b
21
= b
22
=1 x
0
1
=1,569 x
0
3
=2,45 x
0
4
=0,85 α =50 η =10
ξ =50 U
1min
= −1 U
1max
=3 U
2min
=0 U
2max
=1,1
x
1
(0) = 2π/3 x
2
(0) = −0,1 x
3
(0) = 1,2 x
4
(0) = 0,4
x
0
3
x
0
3
=2,45 x
0
4
x
1
(0) = 1,569 x
2
(0) = 0 x
3
(0) = 2,45 x
4
(0) = 0,85
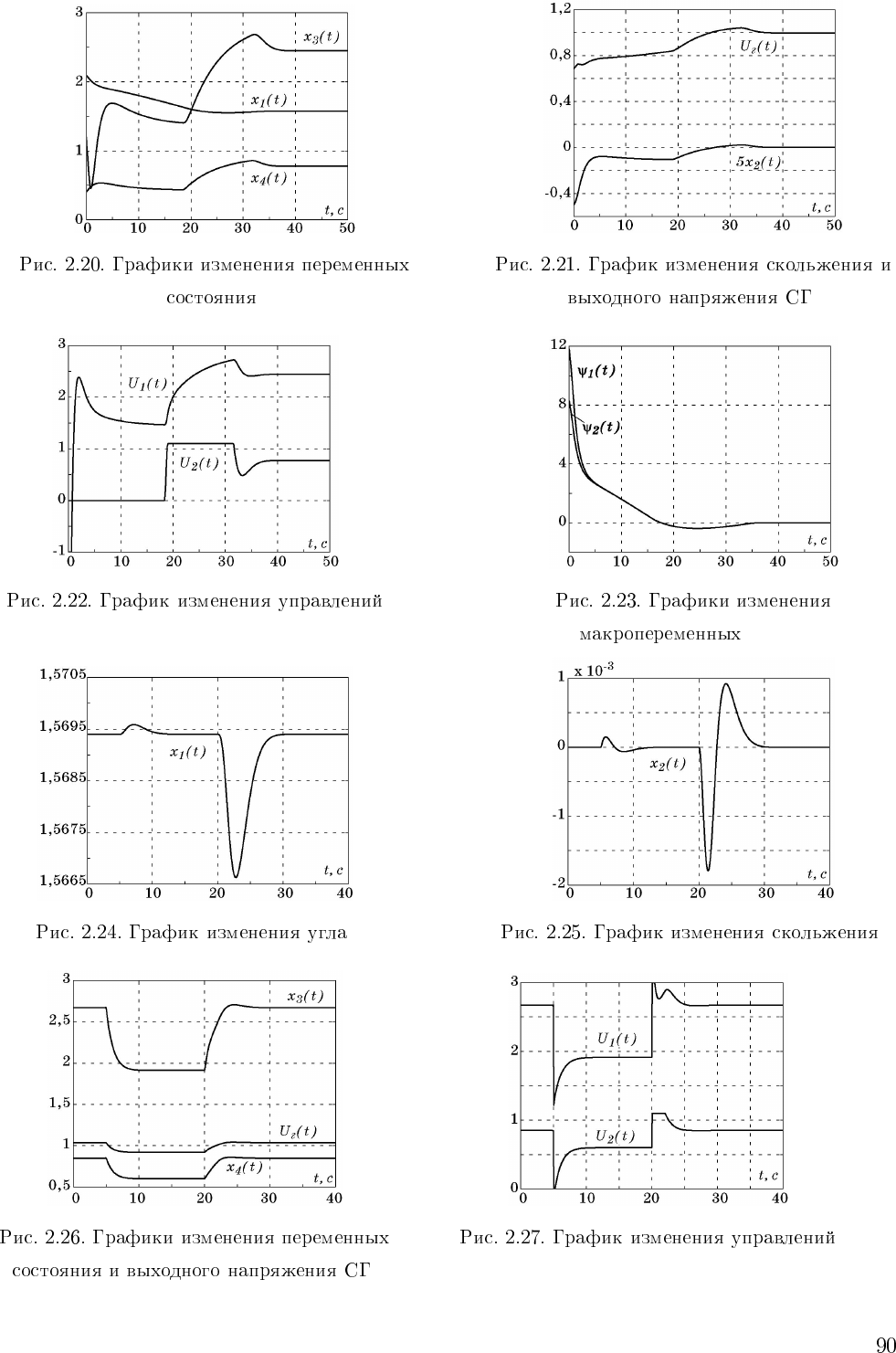
ψ
1
,ψ
2
