Колесников А.А. Синергетические методы управления сложными системами: энергетические системы
Подождите немного. Документ загружается.

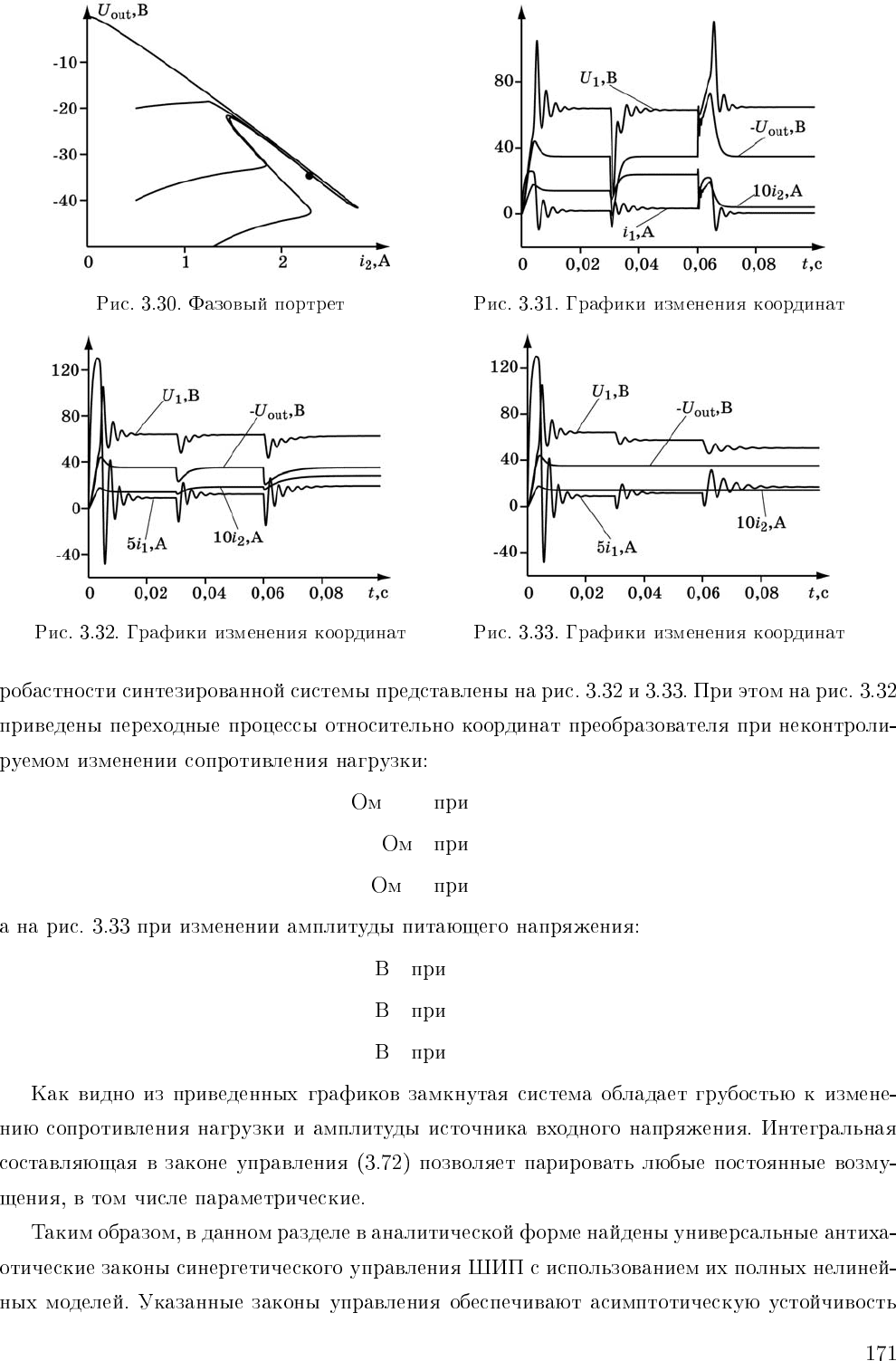
R =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
25
t<0, 03;
18, 75
0, 03 t<0, 06;
12, 5
t 0, 06
E =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
30
t<0, 03;
24
0, 03 t<0, 06;
18
t 0, 06.


m
r U
out
U
c

U
c
= U
out i
− r
i
i
oi
;
i
oi
=
U
out i
− U
c
r
i
,
i U
out i
i r
i
i−
U
c
r
r
U
out
U
out
r
U
out
r

m
C
ext
) R
ext
)
P
load
)
•
•
• E
i
•
•

⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
dz
dt
= η · (U
out
− U
c
);
dU
out
dt
=
1
C
t
m
j=1
i
Lj
−
U
out
R
ext
C
t
−
P
load
U
out
· C
t
+ δ · z;
di
L1
dt
= −
1
L
1
U
out
+
d
c1
E
1
L
1
;
...
di
Lm
dt
= −
1
L
m
U
out
+
d
cm
E
m
L
m
,
U
out
i
Li
d
ci
i
z δ η U
c
C
t
= C
1
+ C
2
+ ...+ C
m
+ C
ext
U
out
= U
c
.

⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
U = U
out
− U
c
;
i
1
= i
L1
;
i
2
= i
L2
;
...
i
m
= i
Lm
,
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
dz
dt
= η · U;
dU
dt
=
1
C
t
m
j=1
i
j
−
U + U
c
R
ext
C
t
−
P
load
(U + U
c
) · C
t
+ δ · z;
di
1
dt
= −
1
L
1
· (U + U
c
)+u
1
;
di
2
dt
= −
1
L
2
· (U + U
c
)+u
2
;
...
di
m
dt
= −
1
L
m
· (U + U
c
)+u
m
,
u
i
=
d
ci
· E
i
L
i
,i= 1,m
ψ
i
= a
i1
· M + a
i2
· U +
m
j=1
a
i,j+2
i
j
+
a
in+1
U + U
c
,i= 1,m,
Ψ = Ai − b,
Ψ =(ψ
1
,ψ
2
, ...ψ
m
)
T
A =
⎛
⎜
⎜
⎜
⎜
⎜
⎝
a
13
a
14
... a
1n
a
23
a
24
... a
2n
... ... ... ...
a
m3
a
m4
... a
mn
⎞
⎟
⎟
⎟
⎟
⎟
⎠
b =
⎛
⎜
⎜
⎜
⎜
⎜
⎝
b
1
b
2
...
b
m
⎞
⎟
⎟
⎟
⎟
⎟
⎠
i =(i
1
,i
2
, ..., i
m
)
T
b
i
= −a
i1
M − a
i2
U −
a
in+1
U + U
c
i = 1,m

ψ
i
a
ij
A
det A =0
T
dΨ
dt
+ Ψ =0,
T =
⎛
⎜
⎜
⎜
⎜
⎜
⎝
T
1
0 ... 0
0 T
2
... 0
... ... ... ...
00... T
m
⎞
⎟
⎟
⎟
⎟
⎟
⎠
m
u = A
−1
· g,
g =
g
1
g
2
... g
m
T
;
g
i
= −
ψ
i
T
i
+
m
j=1
a
ij+2
L
j
−
a
i2
R
ext
· C
t
+
a
in+1
(U + U
c
)
2
· R
ext
· C
t
· (U + U
c
) − η · a
i1
· v−
−
a
i2
−
a
in+1
(U + U
c
)
2
·
m
j=1
i
j
C
t
+ δ · M −
P
load
(U + U
c
) · C
t
; i =
1,m.
j=1,m
ψ
j
=0
T
i
j=1,m
ψ
j
=0
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
dz
ψ
dt
= η · U
ψ
;
dU
ψ
dt
= −
U
ψ
+ U
c
R
ext
C
t
−
P
load
(U
ψ
+ U
c
)
·
1
C
t
+
m
j=1
m
i=1
A
−1
(j, i) ·a
in+1
−
−
m
j=1
m
i=1
A
−1
(j, i) · (a
i1
z
ψ
+ a
i2
U
ψ
)+δ · z
ψ
.
d
2
U
ψ
dt
2
+ F
1
·
dU
ψ
dt
+ F
2
· U
ψ
+
F
3
(U
ψ
+ U
c
)
=0,

F
1
=
1
R
ext
C
t
+
m
&
j=1
m
&
i=1
A
−1
(j, i) · a
i2
F
2
= η ·
m
&
j=1
m
&
i=1
A
−1
(j, i) · a
i1
− δ
F
3
=
1
C
t
+
m
&
j=1
m
&
i=1
A
−1
(j, i) ·a
in+1
· P
load
a
in+1
F
3
d
2
U
ψ
dt
2
+ F
1
·
dU
ψ
dt
+ F
2
· U
ψ
=0
F
1
> 0,F
2
> 0,T
i
> 0,i= 1,m.
1
C
t
+
m
j=1
m
i=1
A
−1
(j, i) ·a
in+1
=0
dU
ψ
dt
+ F
1
· U
ψ
+ F
2
·
U
ψ
dt =0.
j=1,m
ψ
j
=0
U
j=1,m
ψ
j
=0
P
load
=0 a
in+1
=0)
P
load
=0 a
in+1
=0)
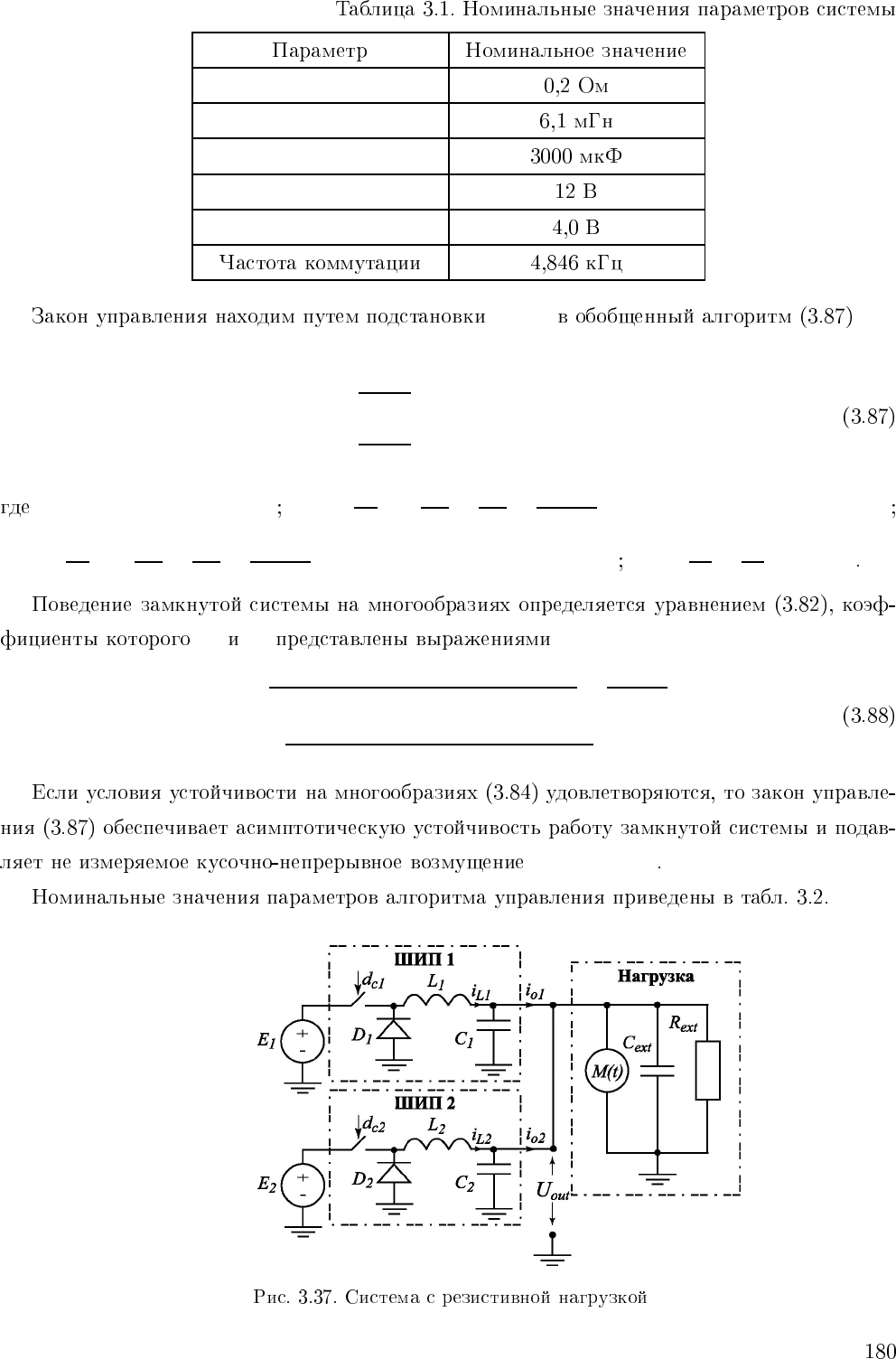
r
L1
= r
L2
= r
Ln
L
1
= L
2
= L
n
C
1
= C
2
= C
n
E
U
c
m =2
u
1
=
1
det A
· (a
24
g
1
− a
23
g
2
);
u
2
=
1
det A
· (−a
14
g
1
+ a
13
g
2
) ,
det A = a
13
·a
24
−a
23
·a
14
g
1
= −
ψ
1
T
1
+
a
13
L
1
+
a
14
L
2
+
a
12
R
ext
C
t
·(U + U
c
) −η ·a
11
·U −a
12
·k
g
2
= −
ψ
2
T
2
+
a
23
L
1
+
a
24
L
2
+
a
22
R
ext
C
t
· (U + U
c
) − η · a
21
· U − a
22
· k k =
i
1
C
t
+
i
2
C
t
+ δ · M
F
1
F
2
F
1
=
a
12
· (a
24
− a
14
)+a
22
· (a
13
− a
23
)
det A
+
1
R
ext
C
t
;
F
2
=
a
11
· (a
24
− a
14
)+a
21
· (a
13
− a
23
)
det A
− δ
· η.
M(t)=const
