Колесников А.А. Синергетические методы управления сложными системами: энергетические системы
Подождите немного. Документ загружается.


dz
dt
=0
U
out
= U
c
dz
dt
=0
z = η
%
(U
c
− U
out
)dt
u(i
L
,U
out
,z)
U
out
= U
c
u(i
L
,U
out
,z)
U
out
= U
c
ψ
1
= i
L
− ϕ,
ψ
1
=0
dψ
1
dt
+ α
1
ψ
1
=0,α
1
> 0,
ϕ(U
out
,z)
ψ
1
=0
dU
out
dt
=
1
C
ϕ −
U
out
R
− z;
dz
dt
= η(U
c
− U
out
),
ψ
2
= U
out
+ γz,
dψ
2
dt
+ α
2
ψ
2
=0,α
2
> 0
ϕ =
U
out
R
+ C(γη(U
c
− U
out
) − α
2
ψ
2
+ z).
ψ
2
=0
dU
out
dt
= z − γη(U
c
− U
out
) − M(t);
dz
dt
= η(U
c
− U
out
).

d
2
U
out
dt
2
− γη
dU
out
dt
− η(U
c
− U
out
)+
dM(t)
dt
=0.
U
out
= U
c
M(t)=M
0
=const
U
out
= U
c
η>0 γ<0
u = −
CLη
E
(γ(α
1
+ α
2
) − 1)(U
c
− U
out
) −
L − RC(L(α
1
+ γη + α
2
− α
1
α
2
RC)+R)
R
2
CE
U
out
−
−
RC(r + L(α
1
+ α
2
− γη))
RCE
i
L
− ηL
1+RC(γη + α
1
α
2
γ − α
1
− α
2
)
RE
(U
c
− U
out
)dt.
ψ
1
=0
U
out
= U
c
L =1, 5 C =10 r =0, 5 E = 800
R =50 α
1
= α
2
= 1000 γ = −600 η =1 U
c
= 400
M(t)=0
M(t)=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
0
t<0, 15;
10
5
0, 15 t<0, 3;
−10
5
t 0, 3

U
out
= U
c
R =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
50
t<0, 025;
25
0, 025 t<0, 06;
5
t 0, 06,
E =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
800
t<0, 025;
760
0, 025 t<0, 06;
720
t 0, 06.
U
out
= U
c
U
out
= U
c

z
di
L
dt
=
E − i
L
r
L
− (1 − u)
U
out
L
;
dU
out
dt
=(1− u)
i
L
C
−
U
out
RC
− z;
dz
dt
= η(U
c
− U
out
).
u(i
L
,U
out
,z)
U
c
= U
out
ψ = i
L
− βU
out
+ γz
dψ
dt
+ αψ =0
u = −
1
CU
out
+ βLi
L
γηLC(U
c
− U
out
)+ηLC(αγ + β)
(U
c
− U
out
)dt − CE+
+
βL − RC(1 + αβL)
R
U
out
+(C(αL − r) − βL)i
L
.
ψ =0
di
L
dt
=
E − i
L
r
L
− (1 −u(U
out
,i
L
,z))
U
out
L
;
dU
out
dt
=(1− u(U
out
,i
L
,z))
i
L
C
−
U
out
RC
−
β
γ
U
out
−
i
L
γ
− M
0
.
V = i
2
L
+
C
L
U
2
out
.
M
0
=0
dV
dt
=2l
L
−
r
L
i
L
− (1 −u(U
out
,i
L
,z))
U
out
L
+
+2
C
L
U
out
(1 − u(U
out
,i
L
,z))
i
L
C
−
1
RC
+
β
γ
U
out
−
i
L
γ
=
= −2
r
L
i
2
L
+
C
L
1
RC
+
β
γ
U
2
out
+
C
Lγ
U
out
i
L
.
U
out
> 0 i
L
> 0
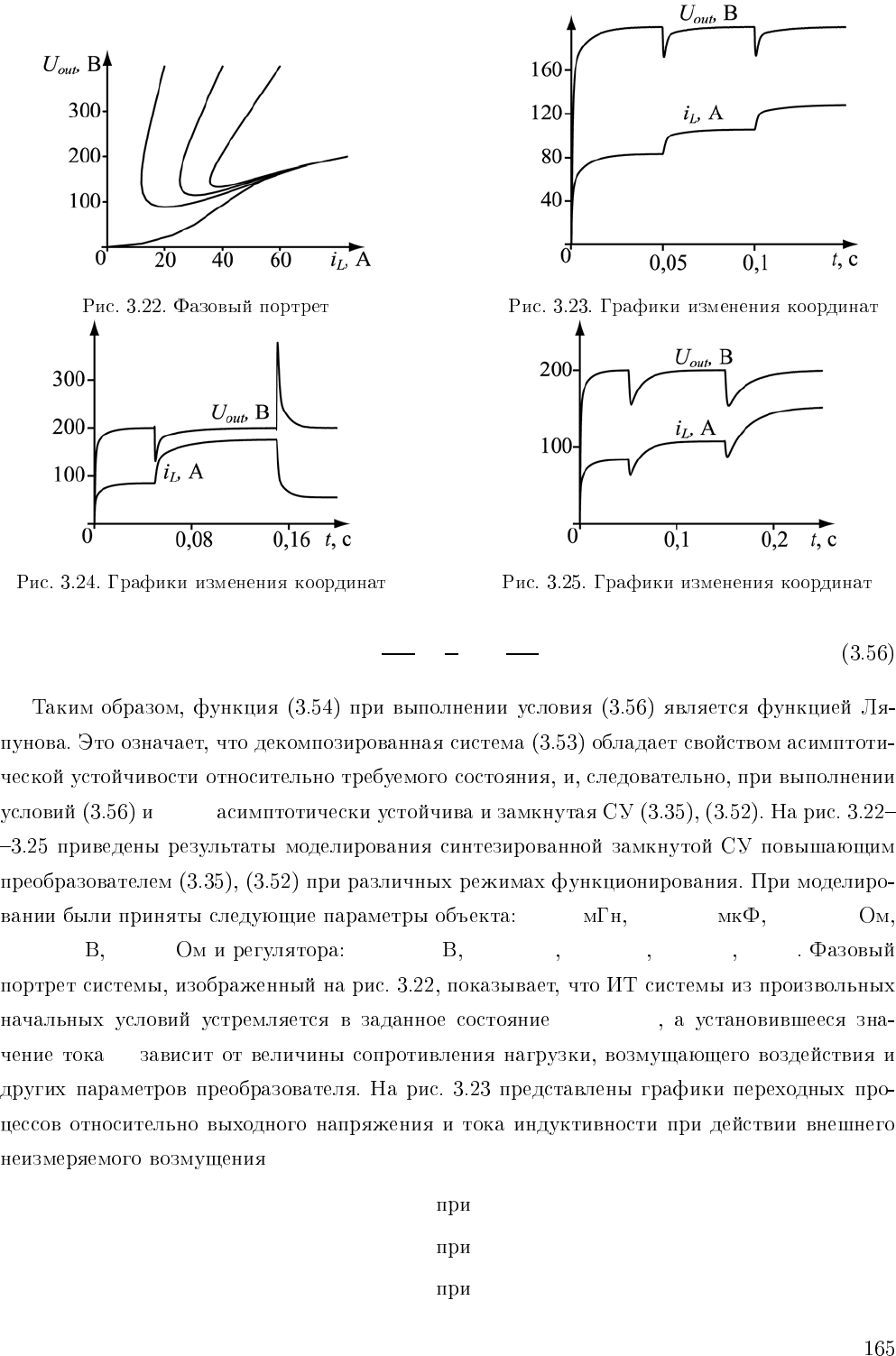
r
1
RC
+
β
γ
>
C
4γ
2
.
α>0
L =1 C = 100 r =0, 05
E = 100 R =5 U
c
= 200 α = 2000 η = −50 β =0, 3 γ =1
U
out
= U
c
i
L
M(t)=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
0
t<0, 05;
10
5
0, 05 t<0, 1;
−10
5
t 0, 1.

U
out
i
L
R =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
5
t<0, 05;
2, 5
0, 05 t<0, 15;
7, 5
t 0, 15
E =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
100
t<0, 05;
80
0, 05 t<0, 15;
60
t 0, 15,
U
out
=
U
c
U
out
= U
c
di
L
dt
=
uE − i
L
r +(1− u)U
out
L
;
dU
out
dt
= −
U
out
RC
− (1 − u)
i
L
C
− z;
dz
dt
= η(U
c
− U
out
).
u =
1
(βLi
L
− C(E − U
out
))R
[((β + αC)L − rC)Ri
L
+(βL(1 − RCα)+RC)U
out
+
+ηRLC
γ(U
c
− U
out
)+(αγ + β)
(U
c
− U
out
)dt
.
U
out
= U
c

i
L
U
out
z = η
%
(U
c
− U
out
)dt
t ≈ (3 ...5)
1
α
ψ =0
M(t)=M
0
=const
di
L
dt
=
u(U
out
,i
L
,z)E − i
L
r +(1− u(U
out
,i
L
,z))U
out
L
;
dU
out
dt
= −
U
out
RC
− (1 − u(U
out
,i
L
,z))
i
L
C
−
β
γ
U
out
+
i
L
γ
− M
0
.
M
0
=0
dV
dt
= −2
r
L
i
2
L
+
C
L
1
RC
+
β
γ
U
2
out
−
C
Lγ
U
out
i
L
.
r
1
RC
+
β
γ
>
C
4γ
2
.
dU
out
dt
=
R
E − ri
L
+ Lη
'
β
%
(U
c
− U
out
)dt + γ(U
c
− U
out
)
(
i
L
+ U
out
(E − U
out
)
R(βLi
L
− C(E − U
out
))
− M
0
.
di
L
dt
≡
dU
out
dt
≡
d
2
U
out
dt
2
≡ 0
RLβηi
L
(U
c
− U
out
)
βri
L
− C(E − U
out
)
−
dM
0
dt
=0.
M
0
=const
%
(U
c
− U
out
)dt
U
out
= U
c
U
out
= U
c
M
0
=const
L =5 C =22 r =0, 02
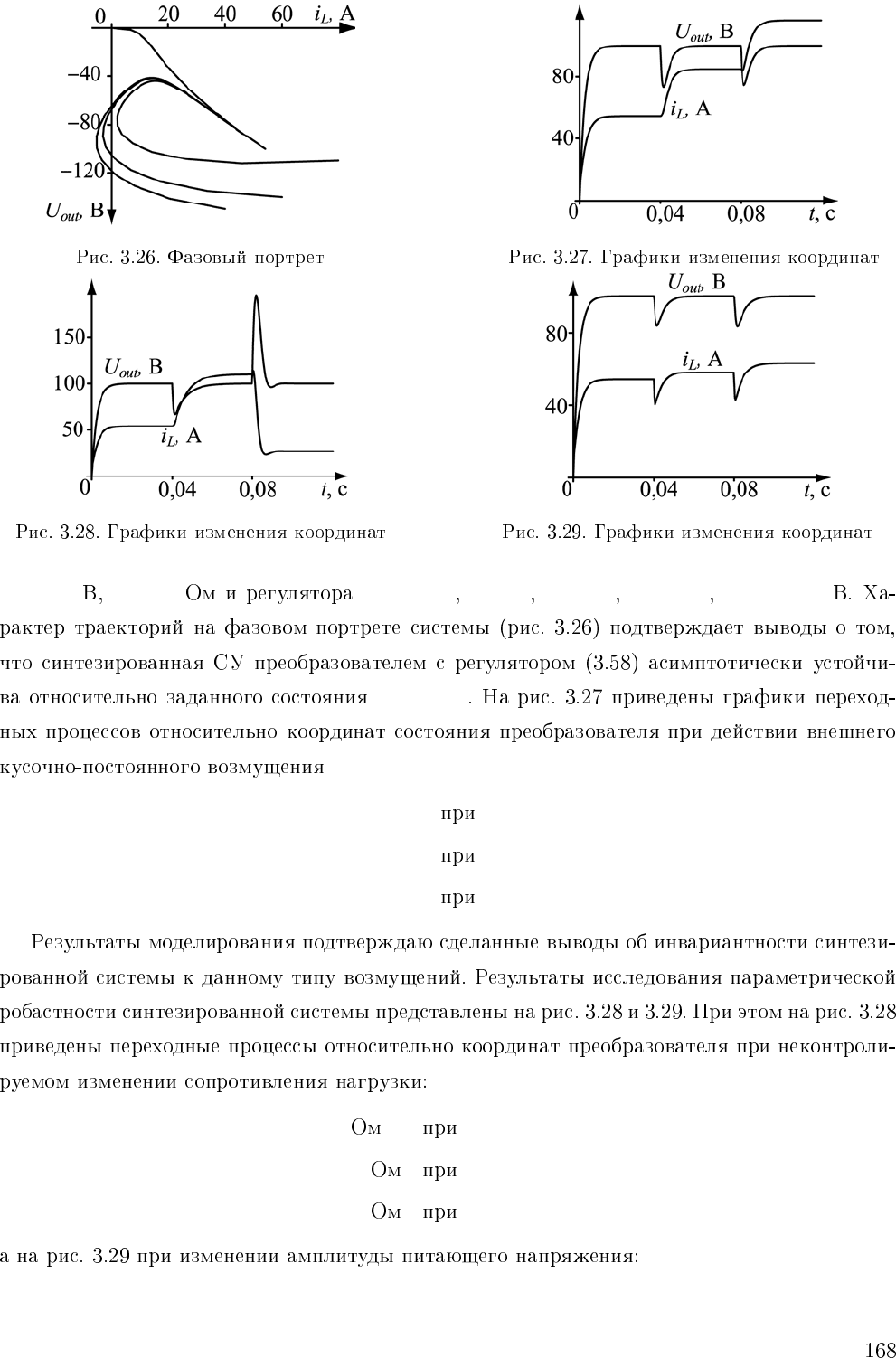
E =60 R =5 α = 1000 β =2 γ =10 η = 100 U
c
= 100
U
out
= U
c
M(t)=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
0
t<0, 05;
10
5
0, 05 t<0, 1;
2 · 10
5
t 0, 1.
R =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
5
t<0, 05;
2, 5
0, 05 t<0, 15;
7, 5
t 0, 15

E =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
100
t<0, 05;
80
0, 05 t<0, 15;
60
t 0, 15,
U
out
= U
c
M
0
= const
dz
dt
= η(U
c
− U
out
).
di
1
dt
=
E − i
1
r
1
− (1 −u)U
1
L
1
;
dU
1
dt
=
i
1
− u(i
1
+ i
2
)
C
1
;
di
2
dt
=
uU
1
− U
out
− i
2
r
2
L
2
;
dU
out
dt
=
i
2
C
2
−
U
out
RC
2
− z;
dz
dt
= η(U
c
− U
out
).
ψ
1
= i
2
− ϕ,
ϕ
ψ
1
=0
dψ
1
dt
+ α
1
ψ
1
=0,α
1
> 0.
ψ
1
=0

di
1
dt
=
E − i
1
r
1
− (1 −u)U
1
L
1
;
dU
1
dt
=
i
1
− u(i
1
+ ϕ)
C
1
;
dU
out
dt
=
ϕ
C
2
−
U
out
RC
2
− z;
dz
dt
= η(U
c
− U
out
).
ψ
2
= U
out
− βz,
ψ
2
=0
dψ
2
dt
+ α
2
ψ
2
=0,α
2
> 0.
ϕ =
1 −α
2
RC
2
R
U
out
+ βηC
2
(U
c
− U
out
)+C
2
(1 + α
2
β)z.
u
u =
a
1
(U
c
− U
out
+ a
2
U
out
+ a
3
i
2
+ a
4
z)
U
1
,
a
1
= ηL
2
C
2
(1 + β(α
1
+ α
2
)) a
2
=1− α
1
α
2
L
2
C
2
+
L
2
R
α
1
+ α
2
+ βη −
1
RC
2
a
3
= r
2
+
L
2
1
RC
2
− α
1
− α
2
− βη
a
4
= L
2
C
2
(α
1
α
2
β + α
1
+ α
2
+ βη) −
1
R
C
1
=10
−4
C
2
=10
−5
r
1
=1
r
2
=0, 5 L
1
=10
−3
L
2
=10
−3
E =30 R =25
α
1
=
1
L
2
α
2
=
1
C
2
η = 100 β =10 U
c
= −35
U
out
= U
c
M(t)=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
0
t<0, 03;
10
5
0, 03 t<0, 06;
−10
5
t 0, 06.
