Коган В.Е., Зенин В.С., Пенкина Н.В. Физическая химия. Часть 2. Химическая кинетика

Подождите немного. Документ загружается.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

()

01 02

kc kc k k x

+− +−

=−−−

. (2.61)

Вынося за скобки

(

)

+−

+ , получим

()()

kkLx

+−

, (2.62)

где через L обозначено

01 02

kc kc

+−

−

. (2.63)

Выражение (2.63), с учетом соотношения (2.60), путем деления числителя и

знаменателя на

−

приведем к виду

01 02

−

. (2.64)

Константу равновесия K, исходя из выражений (2.59), (2.60), определяем по

формуле

02 p

01 p

−

(2.65)

на основании экспериментальных данных.

В уравнении (2.62) разделим переменные

()

kkd

+−

+τ

−

(2.66)

и проинтегрируем полученное выражение (2.66) от 0 до x и от 0 до τ . Обозна-

чая

kkH

+−

= , (2.67)

получим

ln const

τ−

. (2.68)

Величины

L и H, таким образом, могут быть рассчитаны по выражениям (2.64)

и (2.68) на основании опытных данных. Из системы двух уравнений (2.60) и

(2.67) находим

Х и м и ч е с к а я к и н е т и к а

, (2.69)

−

. (2.70)

Таким образом, обратная задача решена.

Для решения прямой задачи сначала выразим

x из уравнений (2.67), (2.68)

и (2.64) в явном виде

()

01 02

Kc c

−

+τ

+−

−

⎡

⎤

=−

⎣

⎦

, (2.71)

а затем, подставив уравнение (2.71) в выражения

101

cc x

− и

202

cc x=+, по-

лучим

()

01 02 01 02

cc Kcc

−

+τ

−

−−

; (2.72)

(

)

()

01 02

Kc c

−

+τ

−

=−

. (2.73)

Значение K находим из соотношения (2.60). Уравнения (2.72) и (2.73) яв-

ляются решением прямой задачи.

Соотношение (2.60) справедливо для обратимой реакции первого поряд-

ка, когда реакция состоит из одной стадии. Константа равновесия обратимых

реакций из двух и более стадий будет определяться константами скоростей

прямой и обратной реакций для каждой стадии. Так, уже

для реакции, состоя-

щей из двух последовательных двусторонних стадий первого порядка, уравне-

ние которой в общем виде

(

)

()

(

)

()

11 2 2

APB

−−−−

⎯⎯⎯⎯→⎯⎯⎯⎯→

←⎯⎯⎯⎯ ←⎯⎯⎯⎯

v v

, (2.74)

константа равновесия будет зависеть от четырех констант скорости. Действи-

тельно, при равновесии

1122

−−

=− =− =vv v v v . (2.75)

В соответствии с законом действующих масс выразим скорости прямых и об-

ратных реакций в первой и второй стадиях через концентрации. Тогда для со-

стояния равновесия получим

p,A11p,P

0kc k c

−

−= и

2p,P 2p,B

0kc k c

−

= . (2.76)

Отсюда

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

11 1p,P

p,A

//cc kk K

−

== и

p,B p,P 2 2 2

//cc kk K

−

= , (2.77)

где

c – концентрация i -го компонента в равновесном состоянии;

–

константы равновесия для первой и второй стадии. С другой стороны, констан-

та равновесия суммарной реакции равна

,B p,A

. Учитывая, что

(

)

(

)

,B p,P p,P p,A p,B p,A

// /cc cc cc= , получаем

−−

==. (2.78)

Таким образом, константа равновесия двустадийной мономолекулярной

реакции связана с четырьмя константами скорости прямых и обратных реакций

в обоих стадиях.

Для рассматриваемой двустадийной реакции, уравнение которой в общем

виде (2.74), скорость можно представить в виде разности двух выражений, про-

порциональных соответственно концентрациям

. Действительно, кон-

центрация промежуточного продукта

c вблизи состояния равновесия стано-

вится очень малой, что позволяет считать процесс квазистационарным (см.

2.2.1.6), а суммарную скорость образования промежуточного вещества

(

)

равной нулю:

()

1 2 1 2 1A 2B 1P 2P

0kc k c k c k c

−− − −

=+ − −= + − − =vvvvv . (2.79)

Определив

c из равенства (2.79)

1A 2B

kc k c

−

(2.80)

и подставив его значение в выражение, например, для скорости первой стадии

реакции, уравнение которой в общем виде (2.74), получим формулу

(

)

11A 2B

kkc kc

−−

−

=−

v , (2.81)

которую легко привести к виду

kc kc

+−

−v

, (2.82)

где

Х и м и ч е с к а я к и н е т и к а

−

−−

−

. (2.83)

Выражения (2.83) подтверждают, что у обратимой двустадийной реакции

нет констант скорости

−

прямой и обратной реакций в целом. В действи-

тельности

и k

−

– эффективные величины, которые сложным образом зави-

сят от констант скорости всех стадий. Для более сложных случаев коэффициен-

ты

−

зависят от концентрации компонентов. Данный факт является еще

одним подтверждением вышесказанному, так как константа скорости реакции

зависит только от температуры и природы реактантов.

Рассматривая двусторонние двустадийные реакции, следует отметить

принцип детального равновесия: при равновесии в химической реакции

любая элементарная стадия протекает с одинаковой скоростью как слева

направо, так и справа налево

. Из данного принципа следует, что обратная

реакция в тех же условиях

(кроме соотношения концентраций) обязатель-

но протекает через те же стадии, что и прямая

. Например, если реакцию,

уравнение которой в общем виде (2.74), записать в общем виде следующим

уравнением:

(

)

()

(

)

()

22 11

BPA

−− −−

⎯⎯⎯⎯→ ⎯⎯⎯⎯→

←⎯⎯⎯⎯ ←⎯⎯⎯⎯

, (2.84)

то формульная единица B становится реагентом и превращается в формульную

единицу

A, при этом превращение будет происходить по тому же механизму,

что и реакция, уравнение которой в общем виде (2.74), т.е. через промежуточ-

ное вещество P.

Для многих двусторонних реакций (стадий) константа равновесия велика,

что в соответствии с равенством (2.60) означает превышение константы скоро-

сти прямой реакции над константой скорости обратной реакции. В таких

усло-

виях прямую реакцию можно рассматривать как

практически односторон-

нюю

, и соотношение между константами скорости прямой и обратной реакций

(соответственно и между их скоростями) в общем виде выразить как

−+

≤

vv.

Принято считать [1], что к односторонним можно отнести реакции в том слу-

чае, когда 0,01

−+

≤vv. Рассмотрим данный вопрос, имеющий важное практиче-

ское значение, несколько подробнее.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

Вышесказанное можно сформулировать следующим образом: если ско-

рость обратной элементарной реакции значительно меньше прямой

(

)

−+

vv и, следовательно, составляет небольшую долю от нее

−

vv (2.85)

(в рассматриваемом случае

0,01g = ), то реакцию, с погрешностью меньше

заданной величины

100 %g , можно рассматривать как практически одно-

стороннюю

(в рассматриваемом случае 100 0,01 1%

⋅

= ). Следовательно, усло-

вием того, что двустороннюю реакцию, уравнение которой в общем виде (2.55),

можно считать практически односторонней, является соотношение

[см. уравне-

ние (2.57)

]

(

)

(

)

01 02

gk c x k c x

+−

−

≥+. (2.86)

Знак равенства означает, что, пренебрегая вторым слагаемым в уравнении

(2.57), т. е. рассматривая реакцию как одностороннюю, мы допускаем погреш-

ность в оценке скорости реакции

v в 100 %g . Знак неравенства указывает, что

эта ошибка меньше 100 %g .

Любая двусторонняя реакция в начальный период может рассматриваться

как односторонняя. Преобразование выражения (2.86)

[с учетом соотношения

(2.60)

] к виду

kcx

−

≥

−

или

≥

−

(2.87)

позволяет получить формулу для расчета максимального значения

max

, до ко-

торого реакцию можно рассматривать как практически одностороннюю,

01 02

max

gKc c

−

. (2.88)

Расчетную формулу для определения максимального времени

max

, в те-

чение которого реакцию можно рассматривать как практически односторон-

нюю, получаем из выражений (2.67) и (2.68) путем подстановки

max

x= :

max

kk Lx

+−

τ=

+−

. (2.89)

Х и м и ч е с к а я к и н е т и к а

Как уже отмечалось выше, константа равновесия у многих обратимых ре-

акций очень велика, т.е. в равновесном состоянии (при завершении реакции)

концентрация продуктов во много раз превышает концентрацию реагентов.

Константа скорости прямой реакции при этом значительно больше константы

скорости обратной реакции, а кинетика реакции в течение всего времени ее

протекания может

рассматриваться как односторонняя. В то же время следует

четко понимать, что не может быть строго односторонних реакций или стадий.

При приближении к концу реакции в любой системе, в принципе через беско-

нечно большое время, должно установиться состояние равновесия. Все стадии

сложной реакции при приближении к состоянию равновесия становятся дву-

сторонними,

а скорости прямых стадий – близкими по значению к скоростям

обратных. Поэтому лишь в ограниченном интервале изменения концентраций

при протекании реакции в условиях, достаточно удаленных от состояния рав-

новесия, одностадийная реакция или лимитирующая стадия сложной реакции

может рассматриваться как односторонняя.

Параллельные (конкурирующие) реакции – это реакции, в которых ис-

ходное вещество одновременно претерпевает изменение, по крайней мере,

по двум направлениям

. Более обобщенно можно сказать, что если в системе

одновременно протекает несколько реакций, в которых участвует один и

тот же реагент

(или реагенты), давая различные продукты, то реакции на-

зываются

параллельными.

Среди параллельных реакций широко распространены такие, в которых

одно исходное вещество атакует различные связи в молекуле другого. Так, при

хлорировании углеводородов промежуточная частица – атом хлора – атакует

различные C–H-связи углеводорода, в результате чего параллельно образуется

набор хлорпроизводных. Это используют для оценки относительной реакцион-

ной способности различных C–H-связей молекул по отношению к хлору

и дру-

гим веществам.

Важное методическое значение среди параллельных реакций приобрели

конкурирующие реакции, в которых одно вещество (частица) реагирует с

двумя или более веществами

(частицами), так что каждое из них конкури-

рует в реакции за это вещество

(частицу). Распространенность таких реакций

и обусловила тот факт, что параллельные реакции часто называют конкури-

рующими. Изучение кинетики конкурирующих реакций позволяет охарактери-

зовать относительную реакционную способность ряда веществ (частиц) по от-

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

ношению к одному и тому же реагенту. Различные типы конкурирующих реак-

ций рассмотрены, например, в [2].

Примером параллельной реакции является разложение гидроксиламина,

которое одновременно может протекать по двум направлениям:

2322

3NH OH NH N 3H O→++

2322

4NH OH 2NH N O 3H O→++.

Мы ограничимся рассмотрением лишь простейших случаев параллельных

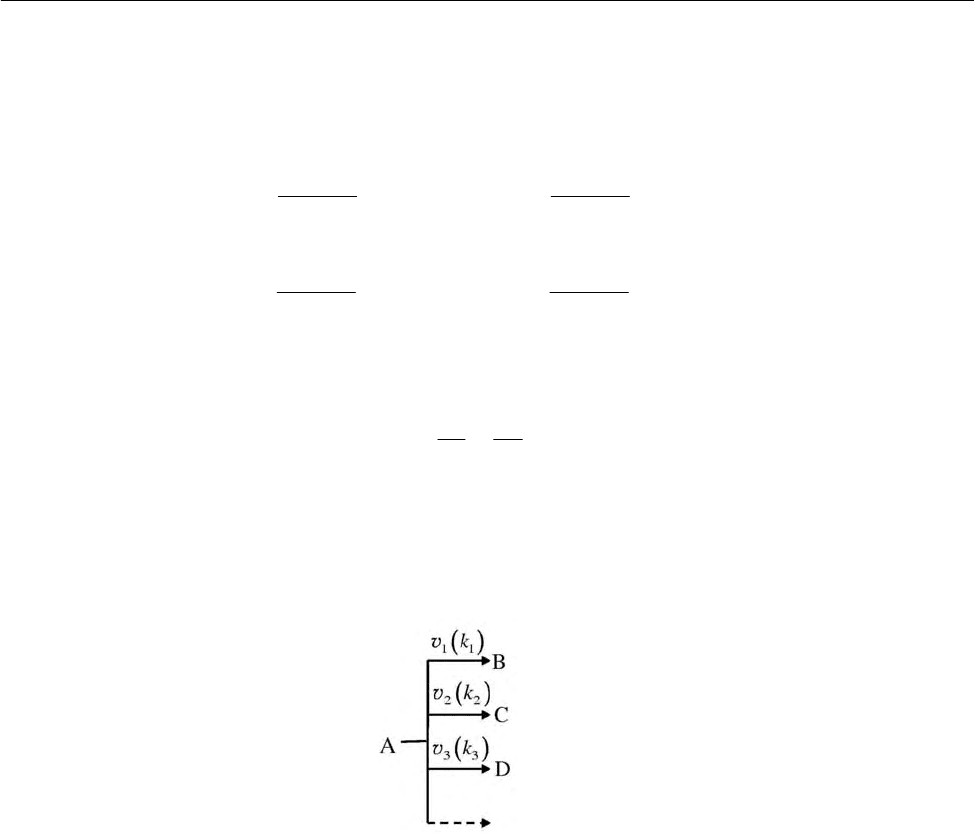
(конкурирующих) реакций. Схему параллельных гомогенных реакций в закры-

той системе, когда реагент A одновременно претерпевает мономолекулярное

превращение в продукты B и D, причем параллельные элементарные односто-

ронние реакции имеют первый порядок по реагенту A, можно представить в

виде

(2.90)

Общая скорость изменения содержания (расходования) реагента A равна

сумме

скоростей реакции по обоим направлениям:

()

11 21 1 2 1

kc k c k k c

−= + =+

, (2.91)

где

c – концентрация реагента A. Уравнение (2.91) после разделения перемен-

ных и интегрирования в пределах от

c до

c и от 0 до

примет вид

(

)

101

cce

−

+τ

= . (2.92)

Скорости образования (получения) продуктов B и D, концентрации кото-

рых соответственно

c и

c , равны

. (2.93)

Подставляя в выражения (2.93) значение

c из уравнения (2.92), получаем

()

2101

dc k c e d

−+τ

τ и

(

)

3201

dc k c e d

−+τ

τ. (2.94)

Х и м и ч е с к а я к и н е т и к а

Предполагая, что в начале реакции

02 03

0cc

= , и интегрируя эти уравнения от

0 до

(или соответственно от 0 до

) получаем, с учетом (2.92), следующие

уравнения:

()

101

2011

12 12

ce cc

kk kk

−+τ

⎡⎤

=− = −

⎣⎦

, (2.95)

()

201

3011

12 12

ce cc

kk kk

−+τ

⎡⎤

=− = −

⎣⎦

. (2.96)

Разделив уравнение (2.95) на уравнение (2.91), получим

. (2.97)

Легко видеть, что на трех (или большем числе) параллельных реакций

первого порядка получится результат, сходный с соотношением (2.97). Так, ес-

ли схему параллельных реакций записать в виде

(2.98)

то уравнение для концентрации

реагента A в экспоненциальной форме будет

иметь вид

(

)

123

101

kk k

cce

−++

= . (2.99)

Концентрации продуктов

(

234

,,ccc соответственно для продуктов

)

B, C, D , при

условии их отсутствия в исходной системе, будут относиться как константы

скорости, т. е.

234 123

: : :... : : :...ccc kkk

(2.100)

Так, при нитровании фенола идут три параллельные реакции первого порядка

(относительно фенола), а именно образование

орто-, мета- и пара-нитрофенолов.

Экспериментально установлено, что отношение количества трех изомеров ос-

тается постоянным в течение всего процесса:

:: 59,2:3,3:3,75 ::

oo мп мп

cc c kk k==.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

Очевидно, что с наибольшей скоростью образуется орто-изомер, а с наимень-

шей –

мета-изомер.

Введем понятие

интегральной селективности процесса (реакции).

Интегральной селективностью процесса при наличии нескольких парал-

лельных реакций называется отношение концентрации основного

(полез-

ного

) продукта к сумме концентраций всех продуктов, полученных в ре-

зультате процесса,

т. е. применительно к реакции, уравнение которой (2.90),

σ=

(2.101)

или, с учетом соотношения (2.97), имеем

σ=

. (2.102)

На основании выражения (2.102)

селективность рассматриваемого процесса

равна соотношению константы скорости основной реакции к сумме кон-

стант скоростей основной и побочной реакций

, если продукт B мы считаем

основным (полезным продуктом), а продукт D – побочным продуктом (отходом

процесса). Для рассматриваемого процесса селективность остается постоянной

на протяжении всего времени протекания двух параллельных реакций. Кинети-

ческие кривые компонентов реакции, уравнение которой (2.90), для случая

cc> , что означает

kk> , т.е. для случая, когда скорость реакции получения

продукта B превышает скорость реакции получения продукта D, приведены на

рис. 2.7. В рассматриваемом случае

главная реакция (как обычно) обладает

большей скоростью, чем

побочная (образование продукта D). Впрочем, при не

слишком большом различии в скоростях, главной (основной) реакцией называ-

ют реакцию, приводящую к получению нужного продукта, хотя бы она и обла-

дала меньшей скоростью.

Таким образом, мы нашли зависимость концен-

трации компонентов A, B и D

от времени [см. выраже-

ния (2.92), (2.95), (2.96)], считая константы скоростей

Рис. 2.7. Кинетические кривые компонентов па-

раллельной реакции, уравнение которой (2.90)

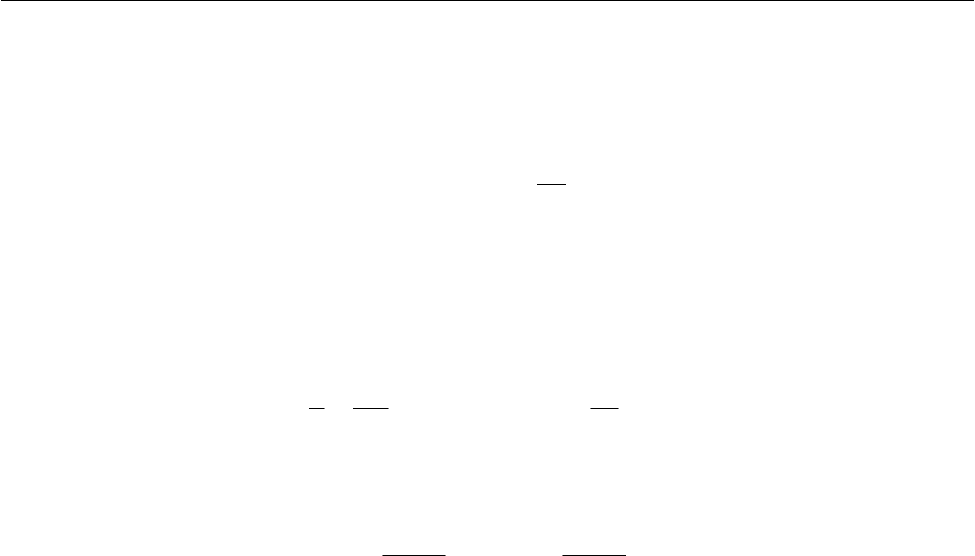
Х и м и ч е с к а я к и н е т и к а

обеих параллельных реакций известными, т. е. решили прямую кинетическую

задачу.

Для решения обратной кинетической задачи введем обозначения

kk M+= и

. (2.103)

Значения величин

M и N рассчитываем, исходя из опытных данных, по форму-

лам (2.104), получаемым, с учетом введенных обозначений (2.103), из уравне-

ний (2.92) и (2.97)

ln const

const

== . (2.104)

Из системы уравнений (2.103) находим

. (2.105)

Проведем качественный анализ параллельной реакции, в которой вещест-

во

вступает во взаимодействие с неустойчивым веществом

, параллельно

распадающимся с константой скорости

k . Уравнения этой реакции в общем

виде следующие:

(

)

(

)

11 2 2

112

A Продукты распада;A A B

⎯⎯⎯→+⎯⎯⎯→

v v

. (2.106)

Если в качестве исходной взята стехиометрическая смесь

A и

A, в конце ре-

акции не будет наблюдаться 100 %-ное превращение

A в B. Это обусловлено

нехваткой вещества

A , которое частично израсходуется на побочную реакцию

первого порядка. При исследовании кинетики реакции по накоплению продукта

B или расходованию реагента

A через определенное время можно зарегистри-

ровать прекращение (остановку) реакции при наличии непрореагировавшего

реагента

A. Наличие избытка реагента

A по сравнению с

A в исходной сме-

си повышает степень превращения. Однако, как показывает строгий математи-

ческий анализ, в реакционной смеси всегда останется некоторое количество не-

прореагировавшего реагента

A, которое тем меньше, чем больше взято реа-

гента

. На рис. 2.8 показано, как выглядят кинетические кривые накопления

продукта

(

)

B c при разных начальных концентрациях реагента

A . Для кине-

тических кривых 1, 2, 3 наблюдается соответственно возрастание начальных