Коган В.Е., Зенин В.С., Пенкина Н.В. Физическая химия. Часть 2. Химическая кинетика

Подождите немного. Документ загружается.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

Формулы (2.52) – различные формы кинетического уравнения реакции

третьего порядка в интегральной форме

. В соответствии с уравнениями

(2.52)

величина

линейно зависит от времени реакции

, что отражает

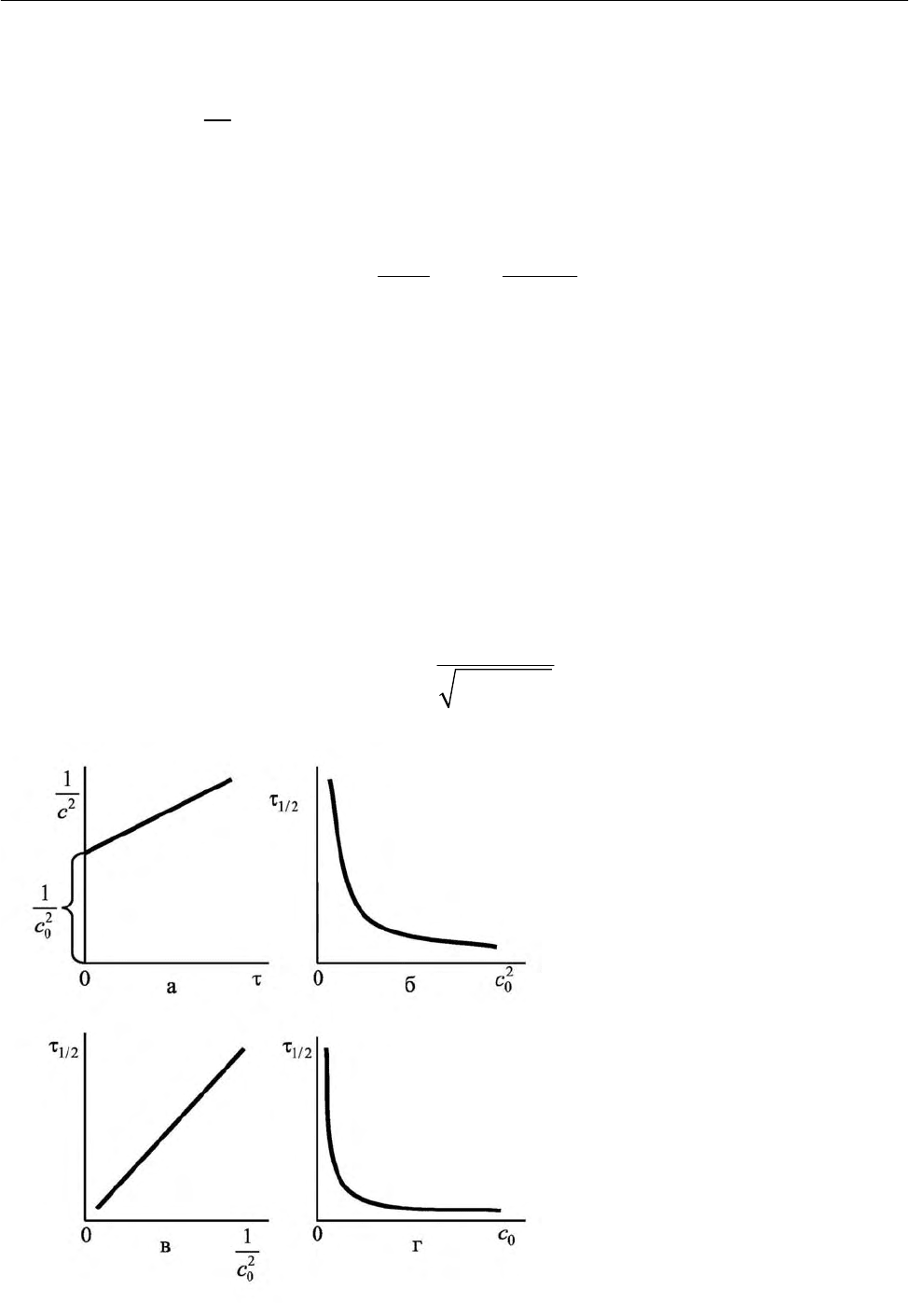
рис. 2.5, а. Уравнения (2.52) позволяют определить время полупревращения и

константу скорости реакции:

1/2

2kc

τ= ,

1/2 0

(2.53)

Итак,

для реакций третьего порядка время полупревращения (уравне-

ние (2.53), рис. 2.5, б, в)

и константа скорости реакции [уравнение (2.53)]

обратно пропорциональны квадрату начальной концентрации реагента

с . Зависимость времени полупревращения (уравнение (2.53), рис. 2.5, г) от

начальной концентрации реагента

– степенная функция.

Если необходимо определить

убыль концентрации x реагента за время

τ, то с учетом

,cc x=− из уравнений (2.52) имеем

⎛⎞

⎜⎟

=−

⎜⎟

⎝⎠

. (2.54)

Полученные для реак-

ций различного порядка кине-

Рис. 2.5. Зависимость обратной

величины квадрата текущей

концентрации от времени про-

цесса (а), времени полупревра-

щения от квадрата начальной

концентрации реагента (б),

времени полупревращения от

обратной величины квадрата

начальной концентрации реа-

гента (в) и времени полупре-

вращения от начальной кон-

центрации реагента (г) для ре-

акции третьего порядка

Х и м и ч е с к а я к и н е т и к а

тические уравнения устанавливают связь между параметрами, характеризую-

щими течение химической реакции

(

)

,,,kc c

, в случаях, когда порядок реак-

ции известен. Если же порядок реакции неизвестен, то его необходимо опреде-

лить.

2.2.1.4. Методы измерения скорости реакции. Способы

определения порядка реакции и расчета

константы скорости реакции

В соответствии с определением понятия (см. 2.2.1.1) измерение скорости

реакции сводится к определению зависимости концентрации реактантов от

времени. Данная задача решается с помощью наиболее подходящих для изу-

чаемого случая методов количественного анализа.

Условно аналитические методы, применяемые в кинетике, можно разде-

лить на химические и физические.

Химический анализ позволяет непосредст-

венно определить концентрации одного из реагентов или продуктов. В то же

время, необходимость быстро сопоставлять результаты с изучаемой реакцией

создает определенные трудности в его применении. Поэтому, когда скорость

аналитической процедуры слишком мала, приходится прибегать к остановке

реакции (ее «замораживанию») путем резкого изменения какого-либо условия

(понижение температуры, удаление катализатора, добавка ингибитора и т. д.).

Преимущество химических методов анализа – получение абсолютных значений

концентраций.

Физические методы анализа, основанные на измерении какого-либо фи-

зического свойства реакционной смеси, изменяющегося в ходе реакции, обычно

удобнее химических. Базируются они на имеющем обычно место наличии су-

щественных различий во вкладах в измеряемое свойство реагентов и продук-

тов. Теоретически для слежения за ходом реакции можно использовать любое

достаточно изменяющееся свойство. Наибольшее распространение

нашли ме-

тоды, связанные с измерением давления при газовой реакции, дилатометрия, а

также различные оптические и электрические методы.

Влияние различных факторов на скорость химической реакции подробно рассматривается в

последующем изложении.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

К преимуществам физических методов анализа следует отнести: быстро-

ту, возможность получения большего числа экспериментальных точек в данный

промежуток времени, отсутствие необходимости отбора пробы и связанных с

этой операцией ошибок, отсутствие влияния на состояние системы, возмож-

ность применения непрерывной автоматической записи изменений свойства.

Однако физические методы не дают непосредственно абсолютных значений

концентраций

. Кроме того, могут появиться ошибки, связанные с самой реак-

цией. Так, например, при спектроскопическом изучении малые количества

сильно окрашенных загрязнений или побочных продуктов могут совершенно

исказить картину. Поэтому для полного изучения какой-либо реакции следует

применять не один, а несколько методов. Особенно желательно это при необ-

ходимости проверки стехиометрии изучаемой

реакции.

Различные способы определения порядка реакции, делящиеся на

диффе-

ренциальные

и интегральные, обобщены и весьма подробно рассмотрены, на-

пример, в [2, 10]. Опытные данные обычно получают по зависимости концен-

трации рассматриваемого реагента от времени в условиях избыточных концен-

траций всех реагентов, кроме исследуемого, т. е. используют

способ избыточ-

ных концентраций

(метод изоляции, или метод избытка). Мы кратко оста-

новимся только на трех интегральных способах (

подстановки, графическом и

определения времени полупревращения), рассмотрев их применительно к ре-

акциям первого, второго и третьего порядков

, протекающих в условиях, сфор-

мулированных в 2.2.1.3.

В этих способах для расчетов используют уравнения кинетических кри-

вых, полученные после интегрирования уравнений вида (2.27), т. е. рассмот-

ренные в 2.2.1.3 кинетические уравнения в интегральной форме.

Способ подстановки основан на использовании уравнений (2.39), (2.46),

(2.52), записанных в следующей форме:

ln при 1

= ; (2.39 а)

при 2

−

τ=; (2.46 а)

Способ подстановки и графический способ неприменимы к реакциям с дробными порядка-

ми по данному реагенту.

Х и м и ч е с к а я к и н е т и к а

при 3

−

= . (2.52 а)

Подставляя в них экспериментальные значения концентрации реагента за раз-

личное время, рассчитывают значения k. Свидетельством того, что эксперимен-

тальные данные характерны для реакции, порядок которой определяется соот-

ветствующим уравнением, служит постоянство расчетных значений k. Напри-

мер, если расчетные значения k остаются постоянными по уравнению (2.46 а),

то порядок реакции по

данному реагенту равен двум.

Графический способ основан на использовании уравнений (2.39), (2.46),

(2.52), записанных в следующей форме:

ln ln при 1ck c n=− τ+ = ; (2.39 б)

при 2kn

=τ+ =; (2.46 б)

2 при 3kn

=τ+ =. (2.52 б)

Из данных уравнений видно, что график, построенный по опытным данным для

концентраций рассматриваемого реагента в разные моменты времени протека-

ния реакции, будет выражаться прямой линией, но в разных координатах для

разных порядков

, а именно: при n = 1 – в координатах ln c

− (рис. 2.3, а); при

n = 1 – в координатах

τ− (рис. 2.4, а); при n = 3 – в координатах

−

(рис. 2.5, а). Если построенный по экспериментальным данным график оказался

линейным, например, в координатах

− , реакцию следует считать реакцией

второго порядка по рассматриваемому реагенту.

После получения линейной зависимости в соответствующих координатах,

не представляет сложности определить графически величину k. Действительно,

в выражениях (2.39 б), (2.46 б), (2.52 б) величины k

−

, k

и 2k

соответственно

являются угловыми коэффициентами, а следовательно, численно равны танген-

Уравнения (2.39 б), (2.46 б), (2.52 б) свидетельствуют о возможности использования и дру-

гих координат. Например, в координатах

τ− ,

⎛⎞

τ− −

⎜⎟

⎝⎠

⎛⎞

τ− −

⎜⎟

⎝⎠

, соответст-

венно при n = 1, 2, 3, также имеем прямую линию, но исходящую из начала координат.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

сам углов наклона прямых к оси времени (ось абсцисс) соответственно для ре-

акций первого, второго и третьего

порядков по рассматриваемому реагенту.

Способ определения времени полупревращения основан на использова-

нии уравнений (2.41), (2.47), (2.53), записанных применительно к времени по-

лупревращения, а именно:

1/2

0,693

при 1n

τ= =; (2.41 а)

1/2

при 2n

τ= =; (2.47 а)

1/2

при 3

τ= =. (2.53 а)

Проводят серию опытов при разных начальных концентрациях и опреде-

ляют время полупревращения исследуемого реагента

. Подтверждение спра-

ведливости того или иного выражения для времени полупревращения указыва-

ет на соответствующий порядок реакции по данному реагенту. Как уже отмеча-

лось (см. 2.2.1.3), при n = 1 время полупревращения не зависит от начальной

концентрации исследуемого реагента (рис. 2.3, б); при n = 2 – обратно пропор-

ционально начальной концентрации (рис. 2.4, б); при n= 3 – обратно пропор-

ционально квадрату начальной концентрации (рис. 2.5, б).

Изложенные выше представления о порядке реакций характерны для од-

носторонних реакций, которые протекают до полного или почти полного обра-

зования продуктов. На практике же в подавляющем большинстве случаев при-

ходится сталкиваться со сложными реакциями, отличными от односторонних.

Нами уже были рассмотрены некоторые вопросы, связанные со

спецификой их

протекания. Однако практическая значимость этих реакций и их широкая рас-

пространенность являются факторами, обусловливающими необходимость, по

При представлении кинетического уравнения в интегральной форме при n = 3 в виде

=τ+

, т. е. графически в координатах

τ−

, угловым коэффициентом, численно

равным тангенсу угла наклона прямой к оси времени, является величина

.k Если по оси ор-

динат отложены значения

ln c− ,

−

или

−

, то знаки угловых коэффициентов, а

следовательно, и направления прямых на графиках, меняются на противоположные.

Другие реагенты берутся в избыточных концентрациях.

Х и м и ч е с к а я к и н е т и к а

крайней мере, краткого независимого рассмотрения сложных химических реак-

ций и особенностей их кинетики.

2.2.1.5. Основные типы сложных химических реакций

Все многообразие сложных реакций можно свести к комбинации не-

скольких типов сложных реакций, а именно:

двусторонних (обратимых), па-

раллельных

и последовательных реакций. Рассмотрение сложных реакций

(как и ранее мы обсуждаем лишь реакции в закрытых системах) упрощается,

если реакция протекает в

квазистационарных условиях (см. подробнее в

2.2.1.6) и имеется

лимитирующая, или скоростьопределяющая стадия.

Как уже отмечалось (см. 2.2.1.2), элементарная (или формально простая)

стадия называется

лимитирующей, когда закономерности всего процесса оп-

ределяются в основном кинетическими закономерностями этой стадии. В слу-

чае

последовательных реакций – это элементарная стадия с константой

скорости, намного меньшей констант скоростей для других последова-

тельных стадий

, т. е. это наиболее медленная стадия сложной последователь-

ной реакции, что полностью оправдывает использование по отношению к ней

термина

«лимитирующая». В случае параллельных реакций – это элемен-

тарная стадия с константой скорости, значительно большей констант ско-

ростей для других параллельных стадий

. Поэтому использование к ней тер-

мина «лимитирующая» носит формальный характер, а ее суть в большей степе-

ни отражает термин

«скоростьопределяющая» (для последовательных реакций

этот термин по своей сути равнозначен термину «лимитирующая»). Из сказан-

ного понятно, что из двух терминов, используемых в формальной кинетике

сложных реакций, наиболее обобщенным является термин «скоростьопреде-

ляющая стадия». В последующем изложении мы будем в равной мере исполь-

зовать оба термина.

Для сложных реакций в закрытых системах

понятие лимитирующая ста-

дия имеет смысл использовать только при

квазистационарном протекании

реакции

, при котором в каждый момент ее состояние соответствует стационар-

ному состоянию в открытой системе.

Рассмотренный в 2.2.1.3, 2.2.1.4 материал позволяет подытожить задачи,

которые применительно к

простым реакциям могут решаться в рамках фор-

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

мальной кинетики на основании основного закона кинетики (с помощью урав-

нений кинетических кривых). Фактически речь шла о трех типах задач [9].

1. Решение вопроса, описывается ли кинетика исследуемой реакции

предлагаемым кинетическим уравнением.

2. Нахождение константы скорости реакции из экспериментальных дан-

ных. Эта задача в химической кинетике называется

обратной задачей.

3. Расчет кинетических кривых для заданных начальных концентраций

компонентов с использованием известных констант скоростей (нахождение

концентрации, соответствующей заданному времени или времени, соответст-

вующему заданной концентрации, есть нахождение одной из точек этой кри-

вой). Эта задача в химической кинетике называется

прямой задачей.

Эти задачи остаются основными и для

сложных химических процессов,

применительно к которым целесообразно более широко определить обратную и

прямую кинетические задачи. В

обратных задачах по опытным кинетическим

кривым находят кинетические параметры (механизм реакции, порядок стадий,

значения констант скорости) элементарных или формально простых стадий ре-

акции, а в

прямых задачах по известным значениям кинетических параметров

сложной реакции находят уравнения кинетических кривых.

При рассмотрении кинетики сложных реакций, как уже отмечалось

(см. 2.2.1.2), используется

принцип независимости, т. е. делается допущение о

том, что величина константы скорости элементарной химической реакции не

зависит от того, протекают ли в данной системе одновременно другие элемен-

тарные реакции. Это допущение равносильно предположению, что протекание

других реакций не нарушает максвелл-больцмановского равновесного распре-

деления реагирующих частиц по скоростям. Другими словами, допускается, что

нарушение равновесного распределения по скоростям (или по энергиям) между

частицами-реагентами в системе, из-за химического превращения формульных

единиц с наиболее высокими энергиями, очень быстро восстанавливается за

счет взаимного обмена энергиями при их столкновениях в процессе хаотиче-

ского теплового движения. Следовательно, принцип независимости постулиру-

ет соблюдение одного из условий выполнимости закона

действующих масс для

простых реакций (см. 2.2.1.2) применительно ко всем элементарным стадиям

сложных реакций. Этот принцип не является, безусловно, общим, так как из-

вестно взаимовлияние реакций, например, при сопряженных реакциях

(см. 2.2.1.7). Однако во многих случаях принцип независимости подтверждает-

ся опытом и его применение плодотворно.

Х и м и ч е с к а я к и н е т и к а

Обратимые реакции – реакции, протекающие в двух направлениях: в

прямом

(получение продуктов из реагентов) и в обратном (образование

реагентов из продуктов

). Поэтому обратимые реакции называют еще двусто-

ронними

. Реакции в своем подавляющем большинстве в той или иной мере об-

ратимы, т. е. не идут до конца, так как в какой-то момент времени устанавлива-

ется равновесие между прямой и обратной реакциями.

Обратимые реакции могут быть различного порядка. В обратимых реак-

циях первого порядка прямая и обратная реакции – реакции

первого порядка.

Если же, по крайней мере, одна из реакций является реакцией второго порядка,

то и обратимая реакция будет второго порядка.

Ограничимся рассмотрением обратимой реакции первого порядка. В об-

щем виде ее уравнение (для одностадийной реакции) можно представить сле-

дующим образом:

(

)

()

−−

⎯⎯⎯→

←

⎯⎯⎯

, (2.55)

где

−

– скорости и константы скорости прямой и обратной эле-

ментарных стадий соответственно.

Наглядным примером обратимой реакции является димеризация диокси-

да азота:

()( )

11 C

224

150 C

2NO N O

газ бурого цвета бесцветные кристаллы

−

⎯⎯⎯⎯→

←⎯⎯⎯⎯

Эта реакция обратима в диапазоне температур от

11 С− до

150 С+ : при

температуре ниже

11 С− идет только прямая реакция с образованием

NO, а

выше

150 С+ – только обратная реакция с образованием

NO . О ходе реакции

судят по изменению цвета.

К обратимым реакциям первого порядка относятся, например, и изомер-

ные превращения в различных классах органических веществ.

Скорость одностадийной двусторонней реакции равна разности ско-

ростей прямой и обратной элементарных реакций

kc kc

+−+ −

=−= −vv v , (2.56)

где

c и

c – концентрации соответственно веществ A и В в момент времени

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

Уравнение (2.56), учитывая, что

101

,cc x

−

202

c с x

+ и что, вследствие

равенства единице стехиометрического коэффициента исходного вещества A

[см. уравнение (2.55)],

=− =

ττ

v , можно переписать в виде

()()

01 02

kc x kc x

+−

=−−+

, (2.57)

где

– начальные концентрации компонентов A и В (при 0τ= ), x – из-

менение концентрации за время

Наиболее существенное отличие обратимых реакций от необратимых со-

стоит в том, что они доходят в пределе

(

)

→∞ не до конца, когда

c→ , а до

состояния равновесия, при котором общая скорость реакции становится равной

нулю:

()()

01 р 02 р

kc x kc x

+−

=−−+=

. (2.58)

Здесь

x – изменение концентрации, которое находят из опыта через достаточ-

но большой промежуток времени после начала реакции, когда система достига-

ет практически равновесного состояния.

Из уравнения (2.58) получаем

02 p

01 p

kcx

−

. (2.59)

Правая часть уравнения (2.59) представляет собой

константу равнове-

сия

. Следовательно,

−

. (2.60)

Итак,

для двусторонней стадии, состоящей из двух элементарных ре-

акций, протекающих в прямом и обратном направлениях, константа рав-

новесия равна отношению их констант скоростей

В данном конкретном случае получена константа равновесия, выраженная через концен-

трацию, т. е.

K . Однако, исходя из того, что сформулированный ниже вывод о равенстве

константы равновесия отношению констант скоростей прямой и обратной элементарных ре-

акций справедлив для всех возможных способов выражения константы равновесия [3], здесь

и далее мы будем для простоты употреблять термин константа равновесия (без уточнения

способа ее выражения) и соответственно обозначение

K .

Х и м и ч е с к а я к и н е т и к а

Приведенный материал является подтверждением одного из условий, ха-

рактеризующего

истинное состояние химического равновесия, а именно: ди-

намический характер равновесия

, т.е. сохранение его вследствие равенства

скоростей прямого и обратного процессов [3].

Следует понимать, что факт остановки обратимой химической реакции

при достижении равновесной концентрации реагента не является основанием

для обратного утверждения. Если реакция остановилась, не дойдя до конца,

нельзя заключить, что достигнуто равновесие. Существует ряд других причин

остановки реакции, например выход

из строя катализатора, необходимого для

протекания изучаемой реакции. Необходим критерий, позволяющий устано-

вить, что остановка реакции обусловлена достижением равновесия (т. е. уста-

новить, что реакция обратима). Наиболее убедительным критерием является

достижение того же состава конечной смеси с другой стороны, т. е. для реакции

(2.55) исходя из продукта B. Из химической термодинамики [3] известно,

что

константа равновесия, т. е. для реакции (2.55) отношение равновесных концен-

траций компонентов B и

A, не зависит от того, каким путем было достигнуто

положение равновесия. В частности, константа равновесия не зависит от того,

исходим из реагента A или из продукта B. Одним из условий, характеризующих

истинное равновесие, и является различие в достижении равновесного со-

стояния

, т. е. подхода к нему с противоположных сторон [3]. Поэтому кинети-

ческие кривые для A должны прийти в обоих экспериментах, как это показано

на рис. 2.6, к одному пределу независимо от того, каковы начальные концен-

трации:

A0A

с c=

0c = – кривая 1 или

B0A

– кривая 2, где

с – кон-

центрация реагента A в прямой элементарной реакции при 0

= .

Из уравнения (2.57) можно вычислить сумму

констант скоростей прямой и обратной реакций

двусторонней стадии. Для этого преобразуем его к

виду

Рис. 2.6. Кинетическая кривая

()

с f=τ обрати-

мой реакции первого порядка при начальных кон-

центрациях:

1 –

A0A

,с c

; 2 –

0,c

B0A

cc=