Kline R.B. Principles and Practice of Structural Equation Modeling

Подождите немного. Документ загружается.

204 CORE TECHNIQuES

the “LISREL Output” command instructs the program to print values of approximate ﬁt

indexes based on C1–C4. See Jöreskog (2004) and Schmukle and Hardt (2005) for more

information about test statistics and approximate ﬁt indexes printed by LISREL under

different combinations of estimation methods and data matrices analyzed.

A brief mention of a statistic known as the normed chi-square (NC) is needed

mainly to discourage you from ever using it. In an attempt to reduce the sensitivity of

the model chi-square to sample size, some researchers in the past divided this statistic

by its expected value, or NC =

/df

, which generally reduced the value of this ratio

compared with

. There are three problems with NC: (1)

is sensitive to sample size

only for incorrect models; (2) df

has nothing to do with sample size; and (3) there were

really never any clear-cut guidelines about maximum values of the NC that are “accept-

able” (e.g., NC < 2.0?—3.0?). Because there is little statistical or logical foundation for

NC, it should have no role in model ﬁt assessment.

aPProXIMate FIt IndeXes

Reviewed in this section are a total of four approximate ﬁt indexes that are among the

most widely reported in the SEM literature. Each describes model ﬁt from a different

perspective. These indexes are as follows.

1. Steiger–Lind root mean square error of approximation (RMSEA; Steiger, 1990),

a parsimony-corrected index, with its 90% conﬁdence interval.

2. Jöreskog–Sörbom Goodness of Fit Index (GFI; Jöreskog & Sörbom, 1982), an

absolute ﬁt index originally associated with LISREL but now also printed by

other programs.

3. Bentler Comparative Fit Index (CFI; Bentler, 1990), an incremental ﬁt index

originally associated with EQS but now also printed by other programs.

4. Standardized Root Mean Square Residual (SRMR), a statistic related to the cor-

relation residuals.

All these indexes are generally available under default ML estimation. When a different

method is used, some of these indexes may not be printed by the computer. Check the

documentation of your SEM computer tool for more information. There are many other

approximate ﬁt indexes in SEM, so many that they could not all be described here in

any real detail. Some older indexes have problems, so it would do little good to describe

them because I could not recommend their use. See Kaplan (2009, chap. 6) or Mulaik

(2009, chap. 15) for more information about other ﬁt statistics in SEM.

Before characteristics of the four indexes just listed are reviewed, we need to

address some critical limitations of basically all approximate ﬁt indexes. These limita-

tions explain why I think it is a bad idea to rely solely on thresholds for approximate ﬁt

indexes when deciding whether or not to respecify a structural equation model:

Hypothesis Testing 205

1. Approximate ﬁt indexes do not demarcate the limit between where expected

levels of chance deviations between the predicted and sample covariance matrices begin

and where evidence against the model begins. This is what the model chi-square test

does.

2. Never ignore evidence of a potentially serious speciﬁcation error indicated by a

failed chi-square test by emphasizing values of approximate ﬁt indexes that look “favor-

able” for your model. That is, do not hide behind approximate ﬁt indexes when there is

other evidence of a potential problem.

3. Although approximate ﬁt indexes are continuous measures, they are not as pre-

cise as they seem for a few reasons: (a) Their values do not reliably or directly indicate

the type or degree of model misspeciﬁcation. For example, there are few (if any) impli-

cations for respeciﬁcation if the value of a goodness-of-ﬁt index with a range of 0–1.0

equals, say, .97 versus .91. (b) The distributions of only some approximate ﬁt indexes are

known under ideal conditions. Whether such conditions hold in real studies is doubtful.

tion studies of a small range of models that were not grossly misspeciﬁed. Evidence that

these thresholds may not generalize to actual studies was summarized earlier.

4. A healthy perspective on approximate ﬁt indexes is to view them as provid-

ing qualitative or descriptive information about model ﬁt. The value of this information

increases when you report values of indexes that as a set assess model ﬁt from different

perspectives, such as the four indexes described next. The drawback is the potential for

obfuscation, or the concealment of evidence about poor ﬁt. This is less likely to happen

if you follow a comprehensive approach to assessing model ﬁt that includes taking the

model chi-square test seriously and describing patterns of residuals.

root Mean square error of approximation

The Root Mean Square Error of Approximation (RMSEA) is scaled as a badness-of-ﬁt

index where a value of zero indicates the best ﬁt. It is also a parsimony-adjusted index

that does not approximate a central chi-square distribution. Instead, the RMSEA theo-

retically follows a noncentral chi-square distribution where the noncentrality parameter

allows for discrepancies between model-implied and sample covariances up to the level

of the expected value of

, or df

. Speciﬁcally, if

≤ df

, then RMSEA = 0, but note

that this result does not necessarily mean perfect ﬁt (i.e., RMSEA = 0 does not say that

= 0). For models where

> df

, the value of RMSEA is increasingly positive. The

formula is

RMSEA =

( 1 )

χ−

−

df N

(8.1)

The model degrees of freedom and one less than the sample size are represented in the

denominator of Equation 8.1. This means that the value of the RMSEA decreases as

there are more degrees of freedom (greater parsimony) or a larger sample size, keeping

all else constant. However, the RMSEA does not necessarily favor models with more

206 CORE TECHNIQuES

degrees of freedom. This is because the effect of the correction for parsimony diminishes

as the sample size becomes increasingly large (Mulaik, 2009). See Mulaik (pp. 342–345)

for more information about other parsimony corrections in SEM.

The population parameter estimated by the RMSEA is often designated as ε (epsi-

lon). In computer output, the lower and upper bounds of the 90% conﬁdence interval for

ε are often printed along with the sample value of the RMSEA, the point estimate of ε.

As expected, the width of this conﬁdence interval is generally larger in smaller samples,

which indicates less precision. The bounds of the conﬁdence interval for ε may not

be symmetrical around the sample value of the RMSEA, and, ideally, the lower bound

equals zero. Both the lower and upper bounds are estimated assuming noncentral chi-

square distributions. If these distributional assumptions do not hold, then the bounds

of the conﬁdence interval for ε may be wrong.

Some computer programs, such as LISREL and Mplus, calculate p values for the

test of the one-sided hypothesis H

: ε

≤ .05, or the close-ﬁt hypothesis. This test is an

accept–support test where failure to reject this null hypothesis favors the researcher’s

model. The value .05 in the close-ﬁt hypothesis originates from Browne and Cudeck

(1993), who suggested that RMSEA ≤ .05 may indicate “good ﬁt.” But this threshold is

a rule of thumb that may not generalize across all studies, especially when distributional

assumptions are in doubt. When the lower limit of the conﬁdence interval for ε is zero, the

model chi-square test will not reject the null hypothesis that ε

= 0 at α = .05. Otherwise,

a model could fail the more stringent model chi-square test but pass the less demand-

ing close-ﬁt test. Hayduk, Pazderka-Robinson, Cummings, Levers, and Beres (2005)

describe such models as close-yet-failing models. Such models should be treated as

any other that fails the chi-square test. That is, passing the close-ﬁt test does not justify

ignoring a failed exact-ﬁt test.

If the upper bound of the conﬁdence interval for ε exceeds a value that may indicate

“poor ﬁt,” then the model warrants less conﬁdence. For example, the test of the poor-

ﬁt hypothesis H

: ε

≥ .10 is a reject–support test of whether the ﬁt of the researcher’s

model is just as bad or even worse than that of a model with “poor ﬁt.” The threshold

of .10 in the poor-ﬁt hypothesis is also from Browne and Cudeck (1993), who suggested

that RMSEA ≥ .10 may indicate a serious problem. The test of the poor-ﬁt hypothesis

can serve as a kind of reality check against the test of the close-ﬁt hypothesis. (The

tougher exact-ﬁt test serves this purpose, too.) Suppose that RMSEA = .045 with the

90% conﬁdence interval .009–.155. Because the lower bound of this interval (.009) is

less than .05, the close-ﬁt hypothesis is not rejected. The upper bound of the same con-

ﬁdence interval (.155) exceeds .10, however, so we cannot reject the poor-ﬁt hypothesis.

These two outcomes are not contradictory. Instead, we would conclude that the point-

estimate RMSEA = .045 is subject to a fair amount of sampling error because it is just as

consistent with the close-ﬁt hypothesis as it is with the poor-ﬁt hypothesis. This type of

“mixed” outcome is more likely to happen in smaller samples. A larger sample may be

required in order to obtain more precise results.

Some limitations of the RMSEA are as follows:

Hypothesis Testing 207

1. Interpretation of the RMSEA and the lower and upper bounds of its conﬁdence

interval depends on the assumption that this statistic follows noncentral chi-square

distributions. There is evidence that casts doubt on this assumption. For example, Ols-

son, Foss, and Breivik (2004) found in computer simulation studies that empirical dis-

tributions from smaller models with relatively few variables and relatively small non-

centrality parameters (less speciﬁcation error) generally followed noncentral chi-square

distributions. Otherwise, the empirical distributions did not typically follow noncentral

chi-square distributions, including models with more speciﬁcation error. These results

and others (e.g., Yuan, 2005) question the generality of the thresholds for the RMSEA

mentioned earlier.

2. Nevitt and Hancock (2000) evaluated in Monte Carlo studies the performance

of robust forms of the RMSEA corrected for non-normality, one of which is based on

the Satorra–Bentler corrected chi-square. Under conditions of data non-normality,

this robust RMSEA statistic generally outperformed the uncorrected version (Equation

8.1).

3. Breivik and Olsson (2001) found in Monte Carlo studies that the RMSEA tends

to impose a harsher penalty for complexity on smaller models with relatively few vari-

ables or factors. This is because smaller models may have relatively few degrees of free-

dom, but larger models may have more “room” for higher df

values. Consequently, the

RMSEA may favor larger models. In contrast, Breivik and Olsson (2001) found that the

Goodness-of-Fit Index (GFI), was relatively insensitive to model size.

goodness-of-Fit Index and Comparative Fit Index

The range of values for this pair of approximate ﬁt indexes is generally 0–1.0 where 1.0

indicates the best ﬁt. The Jöreskog–Sörbom GFI is an absolute ﬁt index that estimates

the proportion of covariances in the sample data matrix explained by the model. That is,

the GFI estimates how much better the researcher’s model ﬁts compared with no model

at all (Jöreskog, 2004). A general formula is

GFI =

res

tot

1 −

(8.2)

where C

res

and C

tot

estimate, respectively, the residual and total variability in the sample

covariance matrix. The numerator in the right side of Equation 8.2 is related to the sum

of the squared covariance residuals, and the denominator is related to the total sum of

squares in the data matrix. Speciﬁc calculational formulas depend on the estimation

method (Jöreskog, 2004).

A limitation of the GFI is that its expected values vary with sample size. For exam-

ple, in computer simulation studies of CFA models by Marsh, Balla, and McDonald

(1988), the mean values of the GFI tend to increase along with the number of cases.

As mentioned, the GFI may be less affected by model size than the RMSEA. Values of

the GFI sometimes fall outside of the range 0–1.0. Values > 1.0 can be found with just-

208 CORE TECHNIQuES

identiﬁed models or with overidentiﬁed models where

is close to zero, and values

< 0 are most likely in small samples or when ﬁt is very poor.

The Bentler Comparative Fit Index (CFI) is an incremental ﬁt index that measures

the relative improvement in the ﬁt of the researcher’s model over that of a baseline

model, typically the independence model. For models where

≤ df

, CFI = 1.0; oth-

erwise, the formula is

CFI =

χ−

−

χ−

(8.3)

where the numerator and the denominator of the expression in the right side of Equation

8.3 estimate the chi-square noncentrality parameter for, respectively, the researcher’s

model and the baseline model. Note that CFI = 1.0 means only that

< df

, not that

the model has perfect ﬁt (

= 0). The CFI is a rescaled version of the Relative Noncen-

trality Index (McDonald & Marsh, 1990), the values of which can fall outside the range

0–1.0. This is not true of the CFI.

All incremental ﬁt indexes have been criticized when the baseline model is the

independence model, which is almost always true. This is because the assumption of

zero covariances among the observed variables is improbable in most studies. There-

fore, ﬁnding that the researcher’s model has better relative ﬁt than the corresponding

independence model may not be very impressive. Although it is possible to specify a

different, more plausible baseline model—such as one that allows the exogenous vari-

ables only to covary—and compute by hand the value of an incremental ﬁt index with

its equation, this is rarely done in practice. Widaman and Thompson (2003) describe

how to specify more plausible baseline models. Check the documentation of your SEM

computer program to ﬁnd out the type of baseline model it assumes when calculating

the CFI.

The CFI depends on the same distributional assumptions as the RMSEA, so values

of the CFI may not be accurate when these assumptions are not tenable. Hu and Bentler

(1999) suggested using the CFI together with an index based on the correlations residu-

als described next, the SRMR. Their rationale was that the CFA seemed to be most sen-

sitive to misspeciﬁed factor loadings, whereas the SRMR seemed most sensitive to mis-

speciﬁed factor covariances in CFA when testing measurement models. Their combina-

tion threshold for concluding “acceptable ﬁt” based on these indexes was CFI ≥ .95 and

SRMR ≤ .08. This combination rule was not supported in Monte Carlo studies by Fan

and Sivo (2005), who suggested that the original Hu and Bentler (1999) ﬁndings about

the CFI and SRMR were artifacts. Results of other computer studies also do not support

the respective thresholds just listed for this pair of indexes (e.g., Yuan, 2005).

standardized root Mean square residual

The indexes described next are based on covariance residuals, differences between

observed and predicted covariances. Ideally, these residuals should all be about zero for

acceptable model ﬁt. A statistic called the Root Mean Residual Square (RMR) was origi-

Hypothesis Testing 209

nally associated with LISREL but is now calculated by other SEM computer tools, too.

It is a measure of the mean absolute covariance residual. Perfect model ﬁt is indicated

by RMR = 0, and increasingly higher values indicate worse ﬁt. One problem with the

RMR is that because it is computed with unstandardized variables, its range depends on

the scales of the observed variables. If these scales are all different, it can be difﬁcult to

interpret a given value of the RMR.

The SRMR is based on transforming both the sample covariance matrix and the

predicted covariance matrix into correlation matrices. The SRMR is thus a measure of

the mean absolute correlation residual, the overall difference between the observed and

predicted correlations. The Hu and Bentler (1999) threshold of SRMR ≤ .08 for accept-

able ﬁt was not a very demanding standard. This is because if the average absolute cor-

relation residual is around .08, then many individual values could exceed this value,

which would indicate poor explanatory power at the level of pairs of observed variables.

It is better to actually inspect the matrix of correlation residuals and describe their pat-

tern as part of a diagnostic assessment of ﬁt than just to report the summary statistic

SRMR.

vIsual suMMarIes oF FIt

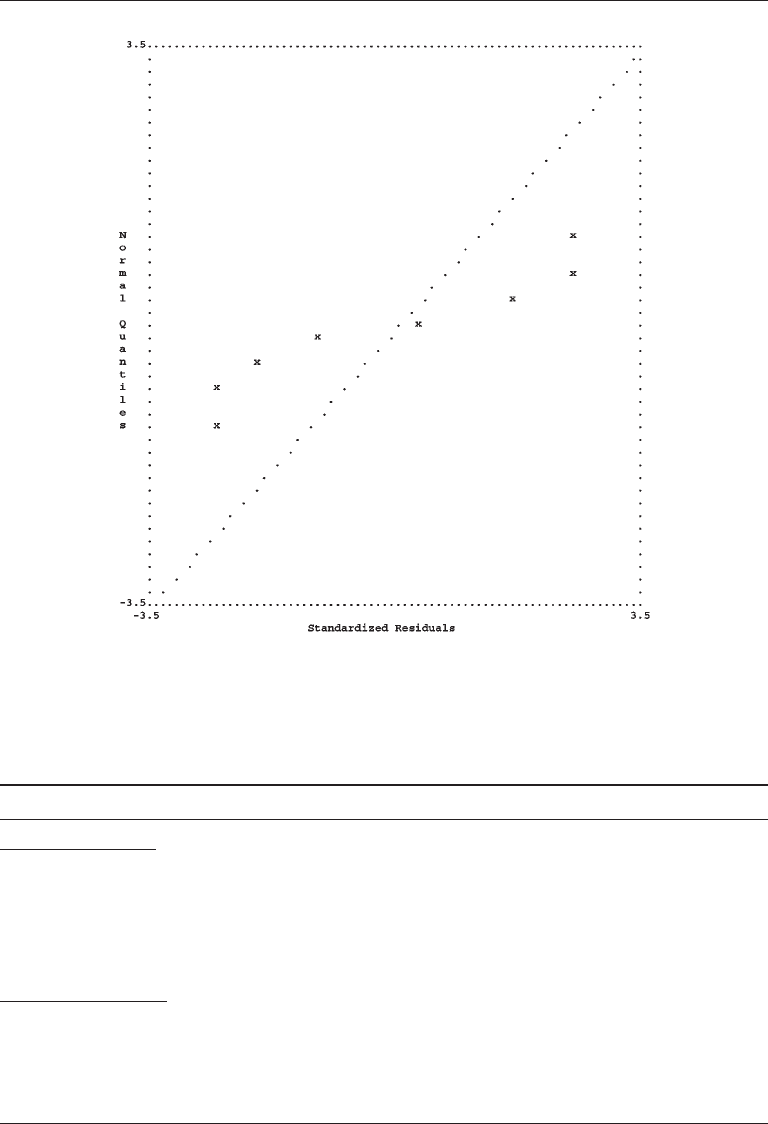
It can be informative to view visual summaries of distributions of the residuals. For

example, frequency distributions of the correlation residuals or covariance residuals

should generally be normal in shape. A quantile-plot (Q-plot) of the standardized resid-

uals (z statistics) ordered by their size and against their expected position in a normal

curve should follow a diagonal line. Obvious departures from these patterns may indi-

cate misspeciﬁcation or violation of the multivariate normality assumption. An example

is presented later in this chapter.

reCoMMended aPProaCh to Model FIt evaluatIon

The method outlined next calls on researchers to report more speciﬁc information about

model ﬁt than has been true of recent practice. The steps are as follows:

1. Always report

—or the appropriate chi-square statistic if the estimation

method is not ML—and its degrees of freedom and p value. If the model fails the exact-

ﬁt test, then explicitly note this fact and acknowledge the need to diagnose both the

magnitude and possible sources of misﬁt. The rationale is to detect statistically signiﬁ-

cant but slight model–data discrepancies that explain the failure. This is most likely to

happen in a very large sample. But even if the model passes the exact-ﬁt test, you still

need to diagnose both the magnitude and possible sources of misﬁt. The rationale is

to detect model–data discrepancies that are not statistically signiﬁcant but still great

enough to cast doubt on the model. This is most likely in a small sample.

210 CORE TECHNIQuES

2. Report the matrix of correlation residuals, or at least describe the pattern of

residuals for a large model. This includes the locations of the larger residuals and their

signs. Look for patterns that may be of diagnostic value in understanding how the model

may be misspeciﬁed.

3. If you report values of approximate ﬁt indexes, then include those for the set

described earlier. If possible, also report the p value for the close-ﬁt hypothesis. Explic-

itly note whether the model fails the close-ﬁt test. Do not try to justify retaining the

model by relying solely on suggested thresholds for approximate ﬁt indexes. This is

especially so if the model failed the chi-square test and the pattern of residuals suggests

a particular kind of speciﬁcation error that is not trivial in magnitude.

4. If you respecify the initial model, then explain your rationale for doing so. You

should also explain the role that diagnostic statistics, such as residuals or other test

statistics described later, played in this respeciﬁcation. That is, point out the connection

between the numerical results for your initial model, relevant theory, and modiﬁcations

of your original model. If you retain a respeciﬁed model that still fails the model chi-

square test, then you must demonstrate that discrepancies between model and data are

truly slight. Otherwise, you have failed to show that there is no appreciable ill covari-

ance-ﬁt evidence that speaks against the model.

5. If no model is retained, then your skills as a scholar are needed to explain the

implications for the theory tested in your analysis. At the end of the day, regardless of

whether or not you retained a model, the real honor comes from following to the best of

your ability the process of science to its logical end. The poet Ralph Waldo Emerson put

it this way: The reward of a thing well done is to have done it.

detaIled eXaMPle

The data set for this example was introduced in Chapter 3. Brieﬂy, Roth et al. (1989)

administered measures of exercise, hardiness—or mental toughness, also a good trait

for learning about SEM— ﬁtness, stress, and illness to 373 university students. The cor-

relations and rescaled standard deviations among these variables are presented in Table

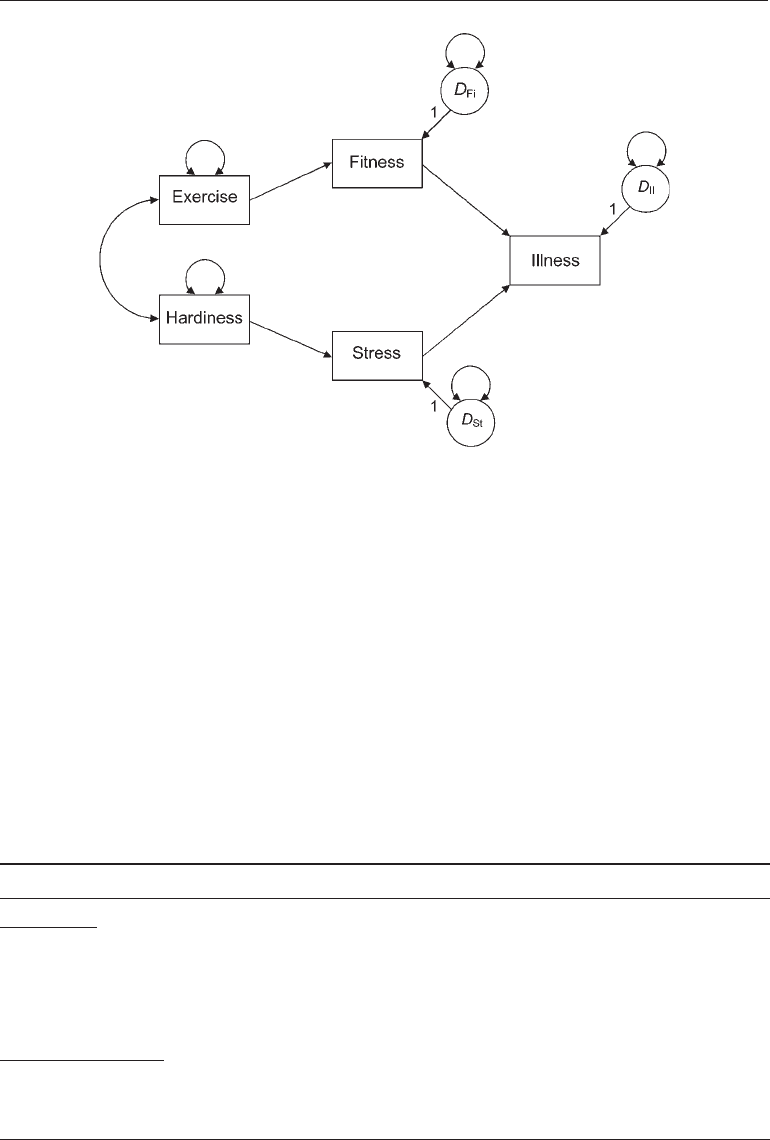
3.4. Presented in Figure 8.1 is one of the recursive path models tested by Roth et al. This

model represents the hypothesis that the effects of exercise and hardiness on illness are

purely indirect and that each effect is transmitted through a single mediator, ﬁtness for

exercise and stress for hardiness. You should verify that the model degrees of freedom

are df

= 5.

The model in Figure 8.1 was ﬁtted to the covariance matrix based on the rescaled

data in Table 3.4 with the ML method of EQS 6.1. You can download the EQS syntax and

output ﬁles from this book’s website (see p. 3) plus all LISREL and Mplus computer ﬁles

for this example. The analysis in EQS converged to an admissible solution. Reported in

Table 8.1 are the estimates of model parameters except for the variances and covariance

of the observed exogenous variables. The latter estimates are just the sample values

(Table 3.4). Brieﬂy, the parameter estimates in Table 8.1 appear logical. For example, the

Hypothesis Testing 211

direct effect of exercise on ﬁtness is positive (the standardized path coefﬁcient is .390),

and higher levels of ﬁtness predict lower illness levels (–.253). Proportions of explained

variance (

smc

) range from .053 for the stress variable to .160 for the illness variable. You

should verify this statement based on the information in Table 8.1.

Presented in column 2 of Table 8.2 are values of ﬁt statistics for the Roth et al.

path model in Figure 8.1. The model chi-square is just statistically signiﬁcant at the .05

level—

(5) = 11.078, p = .049—so the exact-ﬁt hypothesis is rejected. Thus, there is

a need to diagnose the source(s) of this failed test. Values of approximate ﬁt indexes for

FIgure 8.1. A recursive path model of illness factors.

taBle 8.1. Maximum likelihood estimates for a recursive Path Model of Illness

Factors

Parameter Unstandardized

Standardized

Direct effects

Exercise → Fitness

.216** .026 .390

Hardiness → Stress

−.406** .089 −.230

Fitness → Illness

−.424** .080 −.253

Stress → Illness

.287** .044 .311

Disturbance variances

Fitness

1,148.260** 84.195 .848

Stress

4,251.532** 311.737 .947

Illness

3,212,567** 253.557 .840

Note. Standardized estimates for disturbance variances are proportions of unexplained variance.

**p < .01.

212 CORE TECHNIQuES

the Roth et al. model present a mixed picture. The value of the RMSEA is .057, and the

close-ﬁt hypothesis is not rejected (p = .336) based on the value of the lower bound of

the 90% conﬁdence interval, or .001 (see Table 8.2). However, the upper bound of the

RMSEA’s 90% conﬁdence interval, or .103, is large enough so that the poor-ﬁt hypothesis

cannot be rejected. The covariance matrix predicted by the model in Figure 8.1 explains

about 99% of the total variability in the sample covariance matrix (GFI = .988), and

the relative ﬁt of the model is about a 96% improvement over that of the independence

model ﬁt (CFI = .961). Also reported in Table 8.2 are the values of the chi-square statistic

and its degrees of freedom for the independence model.

Presented in Figure 8.2 is a Q-plot of the standardized residuals for the Roth et al.

path model generated by LISREL. In a model with acceptable ﬁt, the points in a Q-plot

of the standardized residuals should fall along a diagonal line, but this is clearly not the

case in the ﬁgure. Altogether, the results in Table 8.2 and the data graphic in Figure 8.2

indicate problems with the ﬁt of the Roth et al. model. But ﬁt statistics and visual sum-

maries do not provide enough detail to further diagnose the apparent sources of these

problems.

Presented in the top part of Table 8.3 are the correlation residuals for the Roth et al.

path model. One of these residuals, –.133 for the ﬁtness and stress variables, exceeds .10

in absolute value. Thus, the model does not explain very well the observed correlation

between these two variables; speciﬁcally, the model underpredicts their association.

Two other correlation residuals in Table 8.3 are close to .10 in absolute value, including

.082 for the ﬁtness and hardiness variables and –.092 for the ﬁtness and illness vari-

ables. The standardized residuals are reported in the bottom part of Table 8.3. The test

for the ﬁtness–stress covariance residual is statistically signiﬁcant (z = 2.563, p < .05).

Other statistically signiﬁcant z tests indicate that the model may not adequately explain

taBle 8.2. values of Fit statistics for two recursive Path Models

Model

Index Roth et al. model (Figure 8.1) Sava model (Figure 7.1)

11.078 3.895

5 7

.049 .791

RMSEA (90% CI)

.057 (.001–.103) 0 (0–.077)

close-ﬁt H

.336 .896

GFI

.988 .989

CFI

.961 1.000

SRMR

.051 .034

165.499 217.131

10 15

Note. CI, conﬁdence interval. Probabilities for the close-ﬁt hypothesis were computed by LISREL. All other

results were computed by EQS.

Hypothesis Testing 213

taBle 8.3. Correlation residuals and standardized residuals for a recursive

Path Model of Illness Factors

Variable 1 2 3 4 5

Correlation residuals

1. Exercise

2. Hardiness

0 0

3. Fitness

0 .082 0

4. Stress

−.057 0 −.133 0

5. Illness

.015 −.092 −.041 .033 .020

Standardized residuals

1. Exercise

2. Hardiness

0 0

3. Fitness

0 1.707 0

4. Stress

−1.125 0 −2.563** 0

5. Illness

.334 −1.944 −2.563** 2.563** 2.563**

Note. The correlation residuals were computed by EQS, and the standardized residuals were computed by

LISREL.

**p < .01.

FIgure 8.2. LISREL-generated quantile plot of standardized residuals for a recursive model

of illness factors.