Kline R.B. Principles and Practice of Structural Equation Modeling

Подождите немного. Документ загружается.

224 CORE TECHNIQuES

and determines the minimum sample size needed to achieve a given level of power for

a test of nested models.

Another option is the Power Analysis module by J. Steiger in

STATISTICA 9 Advanced, which can estimate power for structural equation models over

ranges of ε

(with ε

ﬁxed to its speciﬁed value), α, df

, and N. The ability to inspect

power curves as functions of sample size and other assumptions is useful for planning a

study, especially when grant applications demand power estimates. The Power Analysis

module in STATISTICA also allows the researcher to specify the values of both ε

and

. This feature is handy if there are theoretical reasons not to use the values of these

parameters suggested by MacCallum et al. (1996), such as ε

= .05 and ε

= .08 for the

close-ﬁt hypothesis.

I used the Power Analysis module in STATISTICA 9 to estimate power for tests of

both the close-ﬁt hypothesis and the not-close-ﬁt hypothesis for the Roth et al. path

model of illness factors (Figure 8.1) and the Sava (2002) path model of causes and effects

of teacher–pupil interactions (Figure 7.1). Also estimated for both models are the mini-

mum sample sizes required in order to attain a level of power ≥ .80 for each of the close-

ﬁt and not-close-ﬁt hypotheses. The results are summarized in Table 8.7. For the Roth

et al. model, the estimated power for the test of the close-ﬁt hypothesis is .317. That is,

if this model actually does not have close ﬁt in the population, then the estimated prob-

ability that we can reject this incorrect model is somewhat greater than 30% for a sample

size of 373 cases, given the other assumptions for this analysis (see Table 8.7). For the

same model, the estimated power for the test of the not-close-ﬁt hypothesis is .229. That

is, there is only about a 23% chance of detecting a model with “good” approximate ﬁt

for the Roth et al. analysis. The minimum sample sizes required in order for power to

be at least .80 for tests of the close-ﬁt hypothesis and the not-close-ﬁt hypothesis for the

http://people.ku.edu/~preacher/rmsea/rmsea.htm

taBle 8.7. Power analysis results for two recursive Path Models

Model

Statistic

Roth et al. model

(Figure 8.1)

Sava model

(Figure 7.1)

373 109

5 7

Power

Close-ﬁt test

.317 .153

Not-close-ﬁt test

.229 .096

Minimum N

Close-ﬁt test

1,465 1,075

Not-close-ﬁt test

1,220 960

: ε ≤ .05, ε

= .08, α = .05.

: ε ≥ .05, ε

= .01, α = .05.

Sample size rounded up to closest multiple of 5 required for power ≥ .80.

Hypothesis Testing 225

same model are, respectively, about 1,465 cases and 1,220 cases. Exercise 3 asks you to

interpret the results of the power analysis in Table 8.7 for the Sava (2002) path model,

but it is clear that power for this model is low, too.

The power analysis results just described reﬂect a general trend that power at the

model level may be low when there are few model degrees of freedom even for a rea-

sonably large sample size (e.g., N = 373 for the Roth et al. model of Figure 8.1). For

models with only one or two degrees of freedom, sample sizes in the thousands may

be required in order for model-level power to be greater than .80 (e.g., MacCallum et

al., 1996, p. 144). Sample size requirements for the same level of power drop to some

300–400 cases for models when df

is about 10. Even smaller samples may be needed

for a minimum power of .80 if df

> 20, but the sample size should not be less than 100

in any event. As Loehlin (2004) puts it, the results of a power analysis in SEM can be

sobering. Speciﬁcally, if an analysis has a low probability of rejecting a false model, this

fact should temper the researcher’s enthusiasm for his or her preferred model.

Some other developments in power estimation at the model level are brieﬂy sum-

marized next. MacCallum and Hong (1997) extended MacCallum et al.’s (1996) work on

power analysis at the model level to the GFI and AGFI ﬁt statistics. Kim (2005) studied a

total of four approximate ﬁt indexes, including the RMSEA and CFI, in relation to power

estimation and the determination of sample size requirements for minimum desired lev-

els of power. Kim (2005) found that estimates of power and minimum sample sizes var-

ied as a function of the choice of ﬁt index, the number of observed variables and model

degrees of freedom, and the magnitude of covariation among the variables. This result

is not surprising considering that (1) different ﬁt statistics reﬂect different aspects of

model–data correspondence and (2) there is little direct correspondence between values

of different ﬁt statistics and degrees or types of model misspeciﬁcation. As noted by Kim

(2005), a value of .95 for the CFI does not necessarily indicate the same misspeciﬁcation

as a value of .05 for the RMSEA.

equIvalent and near-equIvalent Models

After a ﬁnal model is selected from among hierarchical or nonhierarchical alternatives,

equivalent models should be considered. Equivalent models yield the same predicted

correlations or covariances but with a different conﬁguration of paths among the same

observed variables. Equivalent models also have equal values of ﬁt statistics, including

(and df

) and all approximate ﬁt indexes. For a given structural equation model,

there are probably equivalent versions. Thus, it behooves the researcher to explain why

his or her ﬁnal model should be preferred over mathematically identical ones.

You already know that just-identiﬁed path models perfectly ﬁt the data. By default,

any variation of a just-identiﬁed path model exactly matches the data, too, and thus is an

equivalent model. Equivalent versions of overidentiﬁed path models—and overidenti-

ﬁed structural models in general—can be generated using the Lee–Hershberger replac-

ing rules (Hershberger, 1994):

226 CORE TECHNIQuES

Within a block of variables at the beginning of the model that is just- (Rule 8.1)

identiﬁed and with unidirectional relations to subsequent variables,

direct effects, correlated disturbances, and equality-constrained recipro-

cal effects (i.e., the two unstandardized direct effects are constrained

to be equal) are interchangeable. For example, Y

→ Y

may be

replaced by Y

→ Y

, D

, or Y



. If two variables are

speciﬁed as exogenous, then an unanalyzed association can be substi-

tuted, too.

At subsequent places in the model where two endogenous variables (Rule 8.2)

have the same causes and their relations are unidirectional, all of the

following may be substituted for one another: Y

→ Y

, Y

→ Y

, and the equality-constrained reciprocal effect Y



Note that substituting reciprocal direct effects for other types of paths would make the

model nonrecursive, but it is assumed that the new model is identiﬁed (Chapter 6).

Some equivalent versions may be implausible due to the nature of the variables or the

time of their measurement. For example, a model that contains a direct effect from an

acculturation variable to chronological age would be illogical. Also, the assessment of Y

before Y

in a longitudinal design is inconsistent with the speciﬁcation Y

→ Y

. When

an equivalent model cannot be disregarded, it is up to you to provide a rationale for pre-

ferring one model over another.

Relatively simple structural models may have few equivalent versions, but more com-

plicated ones may have hundreds or even thousands (see MacCallum, Wegener, Uchino,

& Fabrigar, 1993). In general, more parsimonious structural models tend to have fewer

equivalent versions. You will learn in the next chapter that measurement models can

have inﬁnitely many equivalent versions. Thus, it is unrealistic that researchers consider

all possible equivalent models. As a compromise, researchers should generate at least a

few substantively meaningful equivalent versions. Unfortunately, even this limited step

is usually neglected. Few authors of SEM studies even acknowledge the existence of

equivalent models (e.g., MacCallum & Austin, 2000). This type of conﬁrmation bias is a

pernicious problem in SEM, one that threatens the validity of most SEM studies.

Presented in Figure 8.4(a) is Romney and associates’ original conventional medical

model shown without disturbances to save space. The other three models in Figure 8.4

are generated from the original model using the Lee–Hershberger replacing rules. For

example, the equivalent model of Figure 8.4(b) substitutes a direct effect for a cova-

riance between the illness symptoms and neurological dysfunction variables. It also

reverses the direct effects between diminished SES and low morale and between dimin-

ished SES and neurological dysfunction. The equivalent model of Figure 8.4(c) replaces

two of three direct effects that involve diminished SES with unanalyzed associations.

The equivalent model of Figure 8.4(d) replaces the unanalyzed association between ill-

ness symptoms and neurological dysfunction with an equality-constrained direct feed-

back loop. It also reverses the direct effects between illness symptoms and diminished

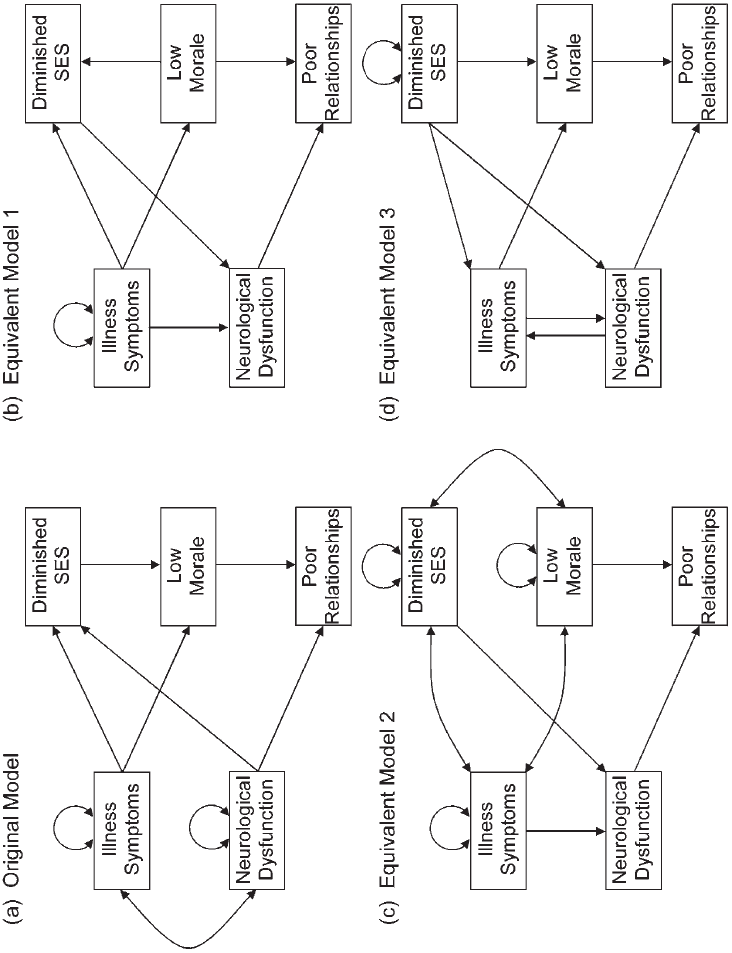
227

FIgure 8.4. Four equivalent path models of adjustment after cardiac surgery. Disturbances are omitted.

228 CORE TECHNIQuES

SES and between neurological dysfunction and diminished SES. Because the models in

Figure 8.4 are equivalent, they all have the same ﬁt to the data (i.e.,

(3) = 3.238 for

each model).

The choice among equivalent models must be based on theoretical rather

than statistical grounds. Exercise 6 asks you to generate equivalent versions of the Sava

(2002) path model in Figure 7.1.

In addition to equivalent models, there may also be near-equivalent models that

do not generate the exact same predicted covariances, but nearly so. For instance, the

path model in Figure 8.1 but with (1) a direct effect from ﬁtness to stress or (2) a direct

effect from stress to ﬁtness are near-equivalent models (see Table 8.4). There is no spe-

ciﬁc rule for generating near-equivalent models. Instead, such models would be speci-

ﬁed according to theory. In some cases, near-equivalent models may be more numer-

ous than truly equivalent models and thus are a more serious research threat than the

equivalent models.

suMMarY

It is critical to begin the testing process with a model that represents a substantive

research problem. The real goal of the analysis is not to ﬁnd a model that ﬁts the data.

Instead, it is to test a theory and then to consider the implications for that theory of

whether or not the model is consistent with the data. There is an ongoing debate in the

SEM literature about optimal strategies for assessing model ﬁt, but there is a general

consensus that some routine practices are inadequate. One bad practice is ignoring a

failed model chi-square test even though the sample size is not very large. Another is

the claim for “good” model ﬁt based mainly on values of approximate ﬁt statistics that

exceed—or, in some cases, fall below—suggested thresholds based on prior computer

simulation studies. Instead, researchers should explicitly diagnose possible sources of

misspeciﬁcation by describing patterns of residuals or values of modiﬁcation indexes for

parameters with a basis in theory. If a model is eventually retained, then it is important

also to estimate statistical power and generate at least a few plausible equivalent or near-

equivalent models. If the statistical power to reject a false model is low or there are few

grounds to prefer the researcher’s model among equivalent versions, then little support

for that model is indicated. The next chapter introduces the analysis of measurement

models with the technique of conﬁrmatory factor analysis.

reCoMMended readIngs

The special issue of the journal Personality and Individual Differences on SEM concerns the

roles of test statistics and approximate ﬁt indexes in model testing (Vernon & Eysenck, 2007).

MacCallum et al. (1993) describe many examples of generating equivalent versions of models

from published articles. Chapter 15 in Mulaik (2009) about model evaluation provides detail

Applying the Lee–Hershberger replacing rules to any of the generated models in Figures 8.4(b)–8.4(d) may

yield even more equivalent versions.

Hypothesis Testing 229

about additional ﬁt statistics and strategies for hypothesis testing. Tomarken and Waller (2003)

consider examples of poor explanatory power for models with apparently “good” ﬁt based on

values of ﬁt statistics. Humphreys (2003) compares the logic of statistical modeling in the social

sciences with that in the natural sciences and ﬁnds many points of contact between the two.

Humphreys, P. (2003). Mathematical modeling in the social sciences. In S. P. Turner & P. A.

Roth (Eds.), The Blackwell guide to the philosophy of the social sciences (pp. 166–184).

Malden, MA: Blackwell.

MacCallum, R. C., Wegener, D. T., Uchino, B. N., & Fabrigar, L. R. (1993). The problem of

equivalent models in applications of covariance structure analysis. Psychological Bulletin,

114 , 185–199.

Mulaik, S. A. (2009). Linear causal modeling with structural equations. New York: CRC Press.

(Chapter 15)

Tomarken, A. J., & Waller, N. G. (2003). Potential problems with “well-ﬁtting” models. Journal

of Abnormal Psychology, 112, 578–598.

Vernon, P. A., & Eysenck, S. B. G. (Eds.). (2007). Structural equation modeling [Special issue].

Personality and Individual Differences, 42(5).

eXerCIses

1. Based on the correlation residuals in Table 7.5, how would you respecify the

Sava path model in Figure 7.1 by adding one path? Fit this respeciﬁed model to

the data in Table 7.1. Evaluate the ﬁt of this revised model.

2. Respecify the Roth et al. path model in Figure 8.1 by adding a direct effect from

ﬁtness to stress. Fit this revised model to the rescaled data in Table 3.4.

3. Interpret the power analysis results in Table 8.7 for the Sava path model in

Figure 7.1.

4. Calculate the AIC for both Romney et al. models in Figure 8.3.

5. Using the MacCallum et al. (1996) article on power analysis, determine the

minimum samples sizes needed to attain a power level of .80 for tests of both

the close-ﬁt hypothesis and the not-close-ﬁt hypothesis at the following values

of df

: 2, 6, 10, 14, 20, 25, 30, and 40. Comment on the results.

6. Generate two equivalent versions of the Sava path model in Figure 7.1. Prove

that these models are in fact equivalent to the original model.

7. Explain why these two models are not equivalent: (a) Figure 8.1 but with the

path Fitness → Stress, (b) Figure 8.1 but with the path Stress → Fitness.

8. Show calculations for the CFI based on the information presented in Table

8.2.

230

Measurement Models and

Conﬁrmatory Factor Analysis

This is the ﬁrst of two chapters about the analysis of core latent variable models in

SEM, in this case measurement models as analyzed in CFA. The multiple-indicator

approach to measurement of CFA represents literally half the basic rationale of analyz-

ing covariance structures in SEM—the analysis of structural models is the other half—so

CFA is a crucial technique. It is also a primary technique for many researchers, espe-

cially those who conduct assessment-related studies. Also introduced in this chapter is

multiple-sample CFA, in which a measurement model is ﬁtted simultaneously to data

from more than one group. The results provide a test of measurement invariance, or of

whether a set of indicators has the same measurement properties across the groups.

If you know something about CFA, then it is easier to learn about structural regression

(SR) models, which have features of both path models and CFA models. The next

chapter covers SR models.

naMIng and reIFICatIon FallaCIes

The speciﬁcation and identiﬁcation of CFA models were introduced in, respectively,

Chapters 5 and 6 using model diagrams where factors were designated with letters,

such as A and B (e.g., Figure 5.6). In real analyses, researchers usually assign meaning-

ful labels to factors such as sequential processing (Figure 5.7). However, it is important

to avoid two logical errors concerning factor names. The ﬁrst is the naming fallacy:

Just because a factor is named does not mean that the hypothetical construct is under-

stood or even correctly labeled. Factors require some type of designation, though, if for

no other reason than communication of the results. Although verbal labels are more

“reader friendly” than more abstract symbols, such as A or ε (xi, a symbol from LISREL’s

Measurement Models and CFA 231

matrix notation for exogenous factors), they should be viewed as conveniences and not

as substitutes for critical thinking.

The second logical error to avoid is reiﬁcation: the belief that a hypothetical con-

struct must correspond to a real thing. For example, a general ability factor, often called

g, is a hypothetical construct. To automatically consider g as real instead of a concept,

however, is a potential error of reiﬁcation. Along these lines, Gardner (1993) reminded

educators not to assume that “intelligence” corresponds to a single domain that is ade-

quately measured by IQ scores. Instead, he argued that intelligence is multifaceted and

includes not only academic skills but also social, artistic, and athletic domains.

estIMatIon oF CFa Models

This discussion assumes that all indicators are continuous variables. This is most likely

to happen when each indicator is a scale that generates a total score over a set of items. A

later section deals with the analysis of models where items are speciﬁed as indicators.

Interpretation of estimates

Parameter estimates in CFA are interpreted as follows:

1. Factor loadings estimate the direct effects of factors on indicators and are inter-

preted as regression coefﬁcients. For example, if the unstandardized factor loading is 4.0

for the direct effect A → X

, then we expect a four-point difference in indicator X

given

a difference of 1 point on factor A. Loadings ﬁxed to 1.0 to scale the corresponding factor

remain so in the unstandardized solution and are not tested for statistical signiﬁcance

because they have no standard errors.

2. For indicators speciﬁed to load on a single factor, standardized factor loadings

are estimated correlations between the indicator and its factor. Thus, squared standard-

ized loadings are proportions of explained variance, or

smc

. If a standardized loading is

.80, for example, the factor explains .80

= .64, or 64.0% of the variance of the indicator.

Ideally, a CFA model should explain the majority of the variance (

smc

> .50) of each

indicator.

3. For indicators speciﬁed to load on multiple factors, standardized loadings are

interpreted as beta weights that control for correlated factors. Because beta weights

are not correlations, one cannot generally square their values to derive proportions of

explained variance.

4. The ratio of an unstandardized measurement error variance over the observed

variance of the corresponding indicator equals the proportion of unexplained variance,

and one minus this ratio is the proportion of explained variance. Suppose that the vari-

ance of X

is 25.00 and that the variance of its error term is 9.00. The proportion of

unexplained variance is 9.00/25.00 = .36, and the proportion of explained variance is

smc

= 1 – .34 = .64.

232 CORE TECHNIQuES

5. Estimates of unanalyzed associations between either a pair of factors or mea-

surement errors are covariances in the unstandardized solution. These estimates are

correlations in the standardized solution.

The estimated correlation between an indicator and a factor is a structure coef-

ﬁcient. If an indicator loads on a single factor, its standardized loading is a structure

coefﬁcient; otherwise, it is not. Graham, Guthrie, and Thompson (2003) remind us that

the speciﬁcation that a direct effect of a factor on an indicator is zero does not mean that

the correlation between the two must be zero. That is, a zero pattern coefﬁcient (factor

loading) does not imply a zero structure coefﬁcient. This is because the factors in CFA

models are assumed to covary, which implies nonzero correlations between each indica-

tor and all factors. However, indicators should have higher estimated correlations with

the factors they are speciﬁed to measure.

Problems

Failure of iterative estimation in CFA can be caused by poor start values; suggestions

for calculating start values for measurement models are presented in Appendix 9.A.

Inadmissible solutions include Heywood cases such as negative variance estimates or

estimated absolute correlations greater than 1.0. Results of some computer studies indi-

cate that nonconvergence or improper solutions are more likely when there are only two

indicators per factor or the sample size is less than 100–150 cases (Marsh & Hau, 1999).

The authors just cited give the following suggestions for analyzing CFA models when

the sample size is not large:

1. Use indicators with good psychometric characteristics that will each also have

relatively high standardized factor loadings (e.g., > .70). Models with indicators that have

relatively low standardized loadings are more susceptible to Heywood cases (Wothke,

1993).

2. Estimation of the model with equality constraints imposed on the unstandard-

ized loadings of indicators of the same factor may help to generate more trustworthy

solutions. This assumes that all indicators have the same metric.

3. When the indicators are items instead of continuous total scores, it may be bet-

ter to analyze them in groups (parcels) rather than individually. Recall that the analysis

of parcels is controversial because it requires a very strong assumption, that the items of

a parcel are unidimensional (Chapter 7).

Solution inadmissibility can also occur at the parameter matrix level. Speciﬁcally,

the computer estimates in CFA a factor covariance matrix and an error covariance

matrix. If any element of either parameter matrix is out of bounds, then that matrix is

nonpositive deﬁnite. Causes of nonpositive deﬁnite parameter matrices include the fol-

lowing (Wothke, 1993):

Measurement Models and CFA 233

1. The data provide too little information (e.g., small sample, two indicators per

factor).

2. The model is overparameterized (too many parameters).

3. The sample has outliers or severely non-normal distributions (poor data screening).

4. There is empirical underidentiﬁcation concerning factor covariances (e.g., Fig-

ure 6.4).

5. The measurement model is misspeciﬁed.

empirical Checks for Identiﬁcation

It is theoretically possible for the computer to generate a converged, admissible solution

for a model that is not really identiﬁed, yet print no warning message. However, that

solution would not be unique. This is most likely to happen in CFA when analyzing a

model with both correlated errors and complex indicators for which the application of

heuristics cannot prove identiﬁcation (Chapter 6). Described next are empirical checks

for solution uniqueness that can be applied when analyzing any type of structural

equation model, not just CFA models. These checks concern necessary but insufﬁcient

requirements. That is, if any of these checks is failed, then the solution is not unique,

but passing them does not prove identiﬁcation:

1. Conduct a second analysis of the same model but use different start values than

in the ﬁrst analysis. If estimation converges to a different solution working from differ-

ent initial estimates, the original solution is not unique and the model is not identiﬁed.

2. This check applies to overidentiﬁed models only: Use the model-implied covari-

ance matrix from the ﬁrst analysis as the input data for a second analysis of the same

model. If the second analysis does not generate the same solution as the ﬁrst, the model

is not identiﬁed.

3. Some SEM computer programs optionally print the matrix of estimated correla-

tions among the parameter estimates. Although parameters are ﬁxed values that do not

vary randomly in the population, their estimates are considered random variables with

their own distributions and covariances. Estimates of these covariances are based on the

information matrix, which is associated with full-information methods such as ML. If

the model is identiﬁed, this matrix has an inverse, which is the matrix of covariances

among the parameter estimates. Correlations among the parameters are derived from

this matrix. An identiﬁcation problem is indicated if any of these absolute correlations is

close to 1.0, which indicates linear dependency. See Bollen (1989, pp. 246–251) for addi-

tional necessary-but-insufﬁcient empirical checks based on linear algebra methods.

detaIled eXaMPle

This example concerns the analysis of the measurement model for the ﬁrst edition Kauf-

man Assessment Battery for Children (KABC -I) introduced in Chapter 5. The two-factor,