Kline R.B. Principles and Practice of Structural Equation Modeling

Подождите немного. Документ загружается.

214 CORE TECHNIQuES

the observed variance of the illness variable or its covariances with the ﬁtness and stress

variables. These diagnostic results indicate that the ﬁt of the path model in Figure 8.1 to

the data in Table 3.4 is unacceptable.

Now look back and scan the ﬁt statistics listed in column 3 of Table 8.2. These results

are for the Sava (2002) path model of causes and effects of teacher–pupil interactions

(Figure 7.1) calculated by LISREL. This model passes both the exact-ﬁt test (

(7) =

3.895, p = .791) and the close-ﬁt test (p = .896). Values of all approximate ﬁt indexes seem

reasonable, too. For example, RMSEA = 0 with .077 as the upper bound of its 90% con-

ﬁdence interval, so the poor-ﬁt hypothesis is rejected. However, recall that this model

has problems concerning its correlation residuals (Table 7.5). Thus, I would conclude that

the ﬁt of this relatively small model is unacceptable despite what the global ﬁt statistics say.

We will see later in this chapter that statistical power is very low for analysis of the Sava

path model in a small sample (N = 109). For the accept–support test provided by

low power favors the researcher’s model (i.e., we are unlikely to detect that this model

is false when it is really is so).

testIng hIerarChICal Models

This section concerns ways to test hypotheses about hierarchical models with the same

data. Two models are hierarchical or nested if one is a proper subset of the other. For

example, if a free parameter is dropped from model A (i.e., the parameter is replaced

with a ﬁxed value that is usually zero) to form model B, the two models are hierarchi-

cally related (model B is nested under model A).

Model trimming and Building

Hierarchical models are compared within two main contexts: model trimming and

building. In model trimming, the researcher typically begins the analysis with a just-

identiﬁed model and simpliﬁes it by eliminating free parameters (paths). This is done

by specifying that at least one path previously estimated freely is now constrained to

equal zero. The starting point for model building is an overidentiﬁed model to which

paths are added. Typically, at least one previously ﬁxed-to-zero path is speciﬁed as a free

parameter. As a model is trimmed, its overall ﬁt to the data usually becomes worse (

increases). Likewise, model ﬁt generally improves as paths are added (

decreases).

The goal of both trimming and building is to ﬁnd the model with the properly speciﬁed

covariance structure that ﬁts the data and is theoretically justiﬁable (keep those eyes on

the prize).

Models can be trimmed or built according to one of two different standards, theo-

retical or empirical. The ﬁrst represents tests of speciﬁc, a priori hypotheses. Suppose

that a path model contains a direct effect of X on Y

and an indirect effect through Y

If the researcher believed that the relation of X to Y

was entirely mediated by Y

, then

he or she could test this hypothesis by constraining the coefﬁcient for the path X → Y

to zero. If the ﬁt of this constrained model is not appreciably worse than the one with

Hypothesis Testing 215

X → Y

as a free parameter, the hypothesis about a mediated relation is supported. The

main point, however, is that respeciﬁcation of a model to test hierarchical versions of it

is guided by the researcher’s hypotheses.

This is not the case for empirically based respeciﬁcation, in which free parameters

are deleted or added according to statistical criteria. For example, if the sole basis for

trimming paths is that their coefﬁcients are not statistically signiﬁcant, then model

respeciﬁcation is guided by purely empirical considerations. The distinction between

theoretically or empirically based respeciﬁcation has implications for interpreting the

results of model trimming or building, which are considered after a model comparison

test statistic is introduced.

Chi-square difference test

The chi-square difference statistic,

, can be used to test the statistical signiﬁcance

of the decrement in overall ﬁt as free parameters are eliminated (trimming) or the

improvement in ﬁt as free parameters are added (building). As its name suggests,

simply the difference between the

values of two hierarchical models estimated with

the same data. Its degrees of freedom, df

, equal the difference between the two respec-

tive values of df

. The

statistic tests the equal-ﬁt hypothesis for two hierarchical

models. Speciﬁcally, smaller values of

lead to failure to reject the equal-ﬁt hypoth-

esis, but larger values lead to its rejection. In model trimming, rejection of the equal-ﬁt

hypothesis suggests that the model has been oversimpliﬁed. The same result in model

building, however, supports retention of the path that was just added. Ideally, the more

complex of the two models compared with

should ﬁt the data reasonably well. Oth-

erwise, it makes little sense to compare the relative ﬁt of two nested models, neither of

which adequately explains the data.

Suppose for an overidentiﬁed model that

(5) = 18.30, p = .003

A direct effect is added to the model (df

is reduced by 1), and the result is

(4) = 9.10, p = .059

Given both results,

= 5 – 4 = 1

(1) = 18.30 – 9.10 = 9.20, p = .002

which says that the overall ﬁt of the new model with an additional path is statistically

better than that of the original model at the .01 level. In this example, the chi-square

difference test is a univariate one because it concerned a single path (df

= 1). When

two hierarchical models that differ by two or more paths are compared (df

≥ 2), the

216 CORE TECHNIQuES

chi-square difference test is essentially a multivariate test of all added (or deleted) paths

together. If p < .05 for

in this case, at least one of the paths may be statistically sig-

niﬁcant at the .05 level if tested individually, but this is not guaranteed.

Note that differences between corrected (scaled) model chi-squares of two hier-

archical models cannot generally be interpreted as a statistic that tests the equal-ﬁt

hypothesis. One corrected model chi-square is the Satorra–Bentler statistic, which is

calculated taking account of the extent of non-normality in the data (Chapter 7). The

difference between the Satorra–Bentler statistics for two hierarchical models ﬁtted to

the same data does not follow a chi-square distribution. However, the researcher can

still compare the relative ﬁts of the hierarchical models to the same data based on each

model’s set of ﬁt statistics (

, RMSEA, SRMR, etc.). If the simpler model has obvi-

ously worse correspondence with the data than the more complex model, the more

complex model would be preferred. (This assumes that the ﬁt of the more complex

model is good.) Otherwise, the simpler model would be favored. Satorra and Bentler

(2001) describe a way to calculate a scaled chi-square difference based on the difference

between the Satorra–Bentler statistics from two hierarchical models, but this method is

not yet widely implemented in SEM computer tools.

empirical versus theoretical respeciﬁcation

The interpretation of

as a test statistic depends in part on whether the new model is

derived empirically or theoretically. For example, if individual paths that are not statisti-

cally signiﬁcant are dropped from the model, it is likely that

will not be statistically

signiﬁcant. But if the deleted path is also predicted in advance to be zero, then

is of

utmost interest. If model speciﬁcation is entirely driven by empirical criteria such as

statistical signiﬁcance, the researcher should worry—a lot, actually—about capitaliza-

tion on chance. That is, a path may be statistically signiﬁcant due only to chance varia-

tion, and its inclusion in the model would be akin to a Type I error. Likewise, a path

that corresponds to a true nonzero causal effect may not be statistically signiﬁcant in a

particular sample, and its exclusion from the model would be essentially a Type II error.

A sort of buffer against the problem of sample-speciﬁc results, though, is a greater role

for theory in model respeciﬁcation.

The issue of capitalization on chance is especially relevant when the researcher

uses an “automatic modiﬁcation” option available in some SEM computer tools such

as LISREL. Such purely exploratory procedures drop or add paths according to empiri-

cal criteria such as statistical signiﬁcance at the .05 level of a modiﬁcation index,

which is calculated for every path that is ﬁxed to zero. A modiﬁcation index is actu-

ally a univariate Lagrange Multiplier (LM),

which in this case is expressed as a

A Lagrange Multiplier is named after the mathematician and astronomer Giuseppe Lodovico Lagrangia

(1736–1813), who is known for his work in the areas of number theory and celestial mechanics. The LM

statistic measures in an estimation algorithm the rate of change in the optimal value of a ﬁt function

as constraints on estimation change. A larger value means a greater potential improvement in the ﬁt

function.

Hypothesis Testing 217

chi-square statistic with a single degree of freedom, or

(1). The value of an LM in

the form of a modiﬁcation index estimates the amount by which the overall model

chi-square statistic,

, would decrease if a particular ﬁxed-to-zero parameter were

freely estimated. That is, a modiﬁcation index estimates

(1) for adding a single path.

Thus, the greater the value of a modiﬁcation index, the better the predicted improve-

ment in overall ﬁt if that path were added to the model. Likewise, a multivariate LM

estimates the effect of allowing a set of constrained-to-zero parameters to be freely

estimated. Some SEM computer tools, such as Amos and EQS, allow the user to gener-

ate modiﬁcation indexes for speciﬁc parameters, which lends a more a priori sense to

this statistic.

Note two cautions about modiﬁcation indexes. First, an SEM computer tool may

print the value of a modiﬁcation index for an “illegal” parameter, such as a covariance

between an exogenous variable and an error term. If you actually tried to add that param-

eter in a subsequent run of the program, the analysis would fail. Second, modiﬁcation

indexes may be printed for a parameter that, if actually added to the model, would make

the respeciﬁed model nonidentiﬁed. Both of these apparently anomalous results are due

to the fact that modiﬁcation indexes merely estimate

(1) values. These estimates are

not derived by the computer actually adding the parameter to the model and rerunning

the analysis. Instead, the computer uses a shortcut method based on matrix algebra that

“guesses” at the value of

, given the covariance matrix and estimates for the more

restricted (original) model.

The Wald W statistic (after the mathematician A. Wald; e.g., Wald, 1943) is a related

index but one used for model trimming. A univariate Wald W statistic approximates the

amount by which the overall

statistic would increase if a particular freely estimated

parameter were ﬁxed to zero (trimmed). That is, a univariate Wald W statistic estimates

(1) for dropping the same path. A value of a univariate Wald W that is not statistically

signiﬁcant at, say, the .05 level predicts a decrement in overall model ﬁt that is not sta-

tistically signiﬁcant at the same level. Model trimming that is entirely empirically based

would thus delete paths with Wald W statistics that are not statistically signiﬁcant. A

multivariate Wald W statistic approximates the value of

for trimming two or more

paths from the model. Loehlin (2004) gives this good advice: A researcher should not feel

compelled to drop from the model every path that is not statistically signiﬁcant, especially

when the sample size is not large. Removing such paths might also affect the solution

in an important way. If there was a theoretical rationale for including the path in the

ﬁrst place, it would be better to leave that path in the model until replication indicates

otherwise.

All of the test statistics just described are sensitive to sample size. Thus, even a

trivial change in overall model ﬁt due to adding or dropping a free parameter could

be statistically signiﬁcant in a very large sample. In addition to noting the statistical

signiﬁcance of a modiﬁcation index, the researcher should also consider the absolute

magnitude of the change in the coefﬁcient for the parameter if it is allowed to be freely

estimated, or the expected parameter change. If the expected change (i.e., from zero)

is small, the statistical signiﬁcance of the modiﬁcation index may reﬂect more the

218 CORE TECHNIQuES

sample size than it does the magnitude of the corresponding effect (see Kaplan, 2009,

pp. 124–126).

speciﬁcation searches

The results of two early computer simulation studies of speciﬁcation searches by Mac-

Callum (1986) and Silvia and MacCallum (1988) are eye opening. They took known

structural equation models, imposed different types of speciﬁcation errors on them,

and evaluated the erroneous models using data generated from populations in which

the known models were true. In MacCallum’s study (1986), models were modiﬁed using

empirically based methods (e.g., modiﬁcation indexes). Most of the time the changes

suggested by empirically based respeciﬁcation were incorrect, which means that they

typically did not recover the true model. The pattern was even more apparent for small

samples (e.g., N = 100). It is not hard to ﬁgure out what went wrong: Purely empirical

respeciﬁcation chases sample-speciﬁc variation and accordingly modiﬁes the model, but

covariance patterns in one sample probably do not precisely mimic those in the popula-

tion. Silvia and MacCallum (1988) followed a similar procedure except that the applica-

tion of automatic modiﬁcation was guided by theoretical knowledge, which improved

the chances of discovering the true model. The implication of these studies is clear:

learn from your data, but your data should not be your teacher (think for yourself).

A relatively new research area in SEM concerns the development of automated yet

“intelligent” speciﬁcation searches based on heuristics that attempt to optimize respeci-

ﬁcation compared with “dumb” speciﬁcation searches (e.g., automatic model modiﬁca-

tion). These algorithms are generally based on principles of machine learning or data

mining. For example, Marcoulides and Drezner (2001) describe an adaptive search algo-

rithm based on principles of genetics and natural selection that evaluates models through

successive “generations” from parent to child models. Marcoulides and Drezner (2003)

describe a search algorithm that mimics the behavior of an ant colony as it collectively

tries to achieve a certain goal, in this case model optimization. Intelligent speciﬁca-

tion searches are not yet widely implemented in SEM computer programs, but this may

change. I am skeptical of any speciﬁcation search method, “intelligent” or otherwise,

that is not guided by reason. Otherwise, such methods may be little more than stepwise

regression dressed in fancy clothes that give the illusion that the researcher does not

have to think about respeciﬁcation.

example of Model Building

Recall that the Roth et al. recursive path model of illness factors (Figure 8.1) does not

have acceptable ﬁt to the data (Table 8.3). In EQS syntax for the analysis of this model, I

requested values of modiﬁcation indexes for all possible direct effects omitted from the

original model, of which there are six altogether (see Figure 8.1). Listed in the middle

column of Table 8.4 are the values of modiﬁcation indexes for these six paths. Note in the

Hypothesis Testing 219

table that (1) the modiﬁcation indexes for two omitted paths, from ﬁtness to stress and

the reverse, are each statistically signiﬁcant; and (2) the values of these indexes are simi-

lar, respectively, 5.357 and 5.096. This means that the addition of either path to the model

would result in about the same estimated decrease in

for the respeciﬁed models.

Now, which respeciﬁed model just mentioned is correct (if either)? It does makes

sense that level of physical ﬁtness would affect the experience of stress: people who are

in better shape may better withstand stress (Fitness → Stress). But is it not also plau-

sible that stress could affect ﬁtness level? For example, highly stressed people may not

perform well on a ﬁtness test (Stress → Fitness). Without theory as a guide, there is no

way to select the most reasonable directionality for a direct effect between stress and ﬁt-

ness. Exercise 2 asks you to analyze a respeciﬁed model for this example with a direct

effect between ﬁtness and stress and then evaluate whether the respeciﬁed model has

acceptable correspondence with the data. I am not suggesting, though, that this is the

correct model.

None of the remaining modiﬁcation indexes in Table 8.4 is statistically signiﬁcant.

They were all calculated for respeciﬁed models with no direct effect between ﬁtness

and stress, but the omission of a path between these variables could be a speciﬁcation

error. This is a limitation of any modiﬁcation index: Speciﬁcation errors elsewhere in

the model could affect its accuracy. (The same is true of covariance and correlation

residuals.) Listed in the third column of Table 8.4 are the

(1) values obtained by actu-

ally adding to the model the direct effect in each row and then rerunning the analysis in

EQS. These results indicate that modiﬁcation indexes only estimate the corresponding

(1) values, although that estimation for this example is close.

CoMParIng nonhIerarChICal Models

Sometimes researchers compare alternative models based on the same variables mea-

sured in the same sample that are not hierarchically related. The values of

from two

nonhierarchical models can be compared, but the difference between them cannot be

interpreted as a test statistic. That is, the chi-square difference test does not apply. This

taBle 8.4. Modiﬁcation Indexes for a recursive Path Model of Illness Factors

Path Modiﬁcation index

(1)

Stress → Fitness

5.357* 5.410*

Fitness → Stress

5.096* 5.157*

Hardiness → Fitness

2.931 2.943

Hardiness → Illness

2.459 2.471

Exercise → Stress

1.273 1.275

Exercise → Illness

.577 .577

*p < .05.

220 CORE TECHNIQuES

is where the family of predictive ﬁt indexes comes in handy. Recall that these statistics

assess model ﬁt in hypothetical replications of the same size randomly selected from the

same population. Perhaps the best known predictive ﬁt index under ML estimation is

the Akaike Information Criterion (AIC). It is based on an information theory approach

to data analysis that combines estimation and model selection under a single conceptual

framework (Anderson, Burnham, & Thompson, 2000). It is also a parsimony-adjusted

index because it may favor simpler models. Confusingly, two different formulas for the

AIC are presented in the SEM literature. The ﬁrst is

AIC

+ 2q (8.4)

where q is the number of free model parameters. Equation 8.4 thus increases the chi-

square for the researcher’s model by a factor of twice the number of freely estimated

parameters. The second formula is

AIC

– 2df

(8.5)

which decreases the model chi-square by a factor of twice the model degrees of freedom.

Although the two formulas are different, the key is that the relative change in the AIC

is the same in both versions, and this change is a function of model complexity. Note

that the relative correction for parsimony of the AIC becomes smaller and smaller as the

sample size increases (Mulaik, 2009).

The AIC and related indexes are generally used in SEM to select among compet-

ing nonhierarchical models estimated with the same data. Speciﬁcally, the model with

the smallest AIC value is chosen as the one most likely to replicate. This is the model

with relatively better ﬁt and fewer free parameters compared with competing models.

In contrast, more complex models with comparable overall ﬁt may be less likely to rep-

licate due to greater capitalization on chance. An example follows. Presented in Figure

8.3 are two different path models of recovery after cardiac surgery evaluated by Rom-

ney, Jenkins, and Bynner (1992). The psychosomatic model of Figure 8.3(a) represents

the hypothesis that patient morale dictates the effects of neurological dysfunction and

diminished socioeconomic status (SES) on physical symptoms and social relationships.

The conventional medical model of Figure 8.3(b) depicts different assumptions about

causal relations among the same variables.

Reported in Table 8.5 are the correlations among the observed variables reported by

Romney et al. for a sample of 469 patients. Unfortunately, Romney et al. did not report

means or standard deviations, and the analysis of a correlation matrix with default ML

estimation is not recommended. To deal with this problem, I used the SEPATH module

of STATISTICA 9 Advanced to ﬁt each model of Figure 8.3 to the correlation matrix in

Table 8.5 using the method of constrained estimation (Chapter 7). Both analyses con-

verged to admissible solutions.

Values of selected ﬁt indexes for the two alternative Romney et al. path models are

reported in Table 8.6. It is no surprise that the overall ﬁt of the more complex conven-

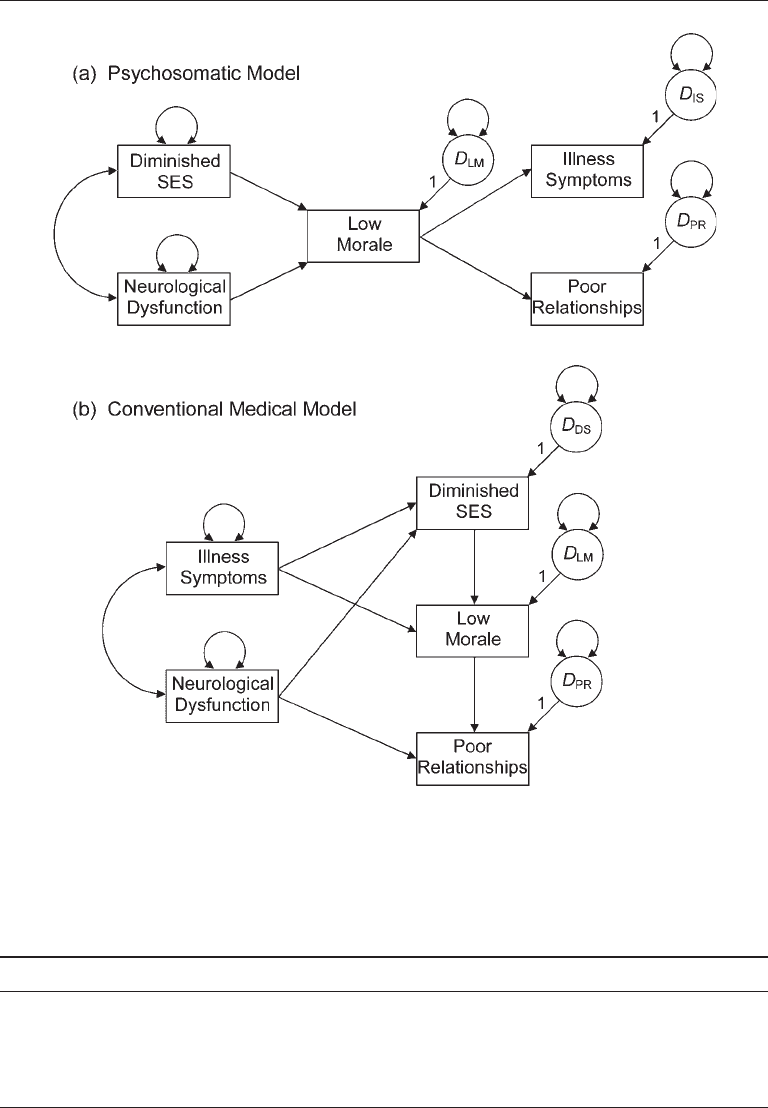
Hypothesis Testing 221

FIgure 8.3. Alternative nonhierarchical recursive path models of adjustment after cardiac

surgery.

taBle 8.5. Input data (Correlations) for analysis of nonhierarchical recursive

Path Models of recovery after Cardiac surgery

Variable 1 2 3 4 5

1. Low Morale

1.00

2. Illness Symptoms

.53 1.00

3. Neurological Dysfunction

.15 .18 1.00

4. Poor Relationships

.52 .29 −.05 1.00

5. Diminished SES

.30 .34 .23 .09 1.00

Note. These data are from Romney et al. (1992); N = 469.

222 CORE TECHNIQuES

tional medical model (df

= 3) is better than that of the more parsimonious psychosomatic

model (df

= 5). But the ﬁt advantage of the more complex model is enough to offset the

penalty for having more free parameters imposed by the AIC as deﬁned by Equation

8.4. For the more complex conventional medical model, AIC = 27.238, but for the psy-

chosomatic model, AIC = 60.402. (Exercise 4 asks you to verify these results.) Because

the former model has the lowest AIC value, it is preferred. This model also passes the

chi-square test, and values of approximate ﬁt indexes are favorable, too (Table 8.6). See

Mulaik (2009, pp. 346–358) for information about other predictive ﬁt indexes.

PoWer analYsIs

Researchers can estimate statistical power at one of two different levels in SEM. The

ﬁrst concerns the power to detect an individual effect (parameter), and the best known

method for estimating the power of single-df tests is one by Saris and Satorra (1993).

Suppose that a researcher believes that the population unstandardized direct effect of X

on Y is 5.0 (i.e., a 1-point increase on X leads to an increase on Y of 5 points holding con-

stant all other causal variables). Using this and other a priori values of the parameters

of the researcher’s model, the researcher next generates a predicted covariance matrix

under the alternative hypothesis (the model includes X → Y) by employing the tracing

rule or methods based on matrix algebra. This model-implied covariance matrix is then

speciﬁed as the input data to an SEM computer program. The model analyzed is the

model under the null hypothesis, which does not include X → Y (it is ﬁxed to zero), and

the sample size speciﬁed is a planned value for the study (e.g., N = 400). The value of

from this analysis approximates a noncentral chi-square statistic. Next, the researcher

consults a special table for noncentral chi-square for estimating power as a function of

degrees of freedom and the level of α (e.g., Loehlin, 2004, p. 263). The researcher uses

df = 1 in these tables to obtain the estimated probability of detecting the added free

parameter when testing for it.

taBle 8.6. values of selected Fit statistics for two nonhierarchical recursive

Path Models of adjustment after Cardiac surgery

Model

Index

Psychosomatic model

(Figure 8.3(a))

Conventional medical model

(Figure 8.3(b))

40.402 3.238

5 3

< .001 .356

RMSEA (90% CI)

.120 (.086–.156) .016 (0–.080)

GFI

.968 .997

CFI

.913 .999

SRMR

.065 .016

Note. CI, conﬁdence interval.

Hypothesis Testing 223

A drawback of the method just described is that it must be repeated for every indi-

vidual parameter for which an estimate of power is desired. An alternative is to use a

Monte Carlo method such as the one implemented in Mplus, which estimates the pro-

portion of generated samples where the null hypothesis that some parameter of interest

equals zero is correctly rejected (Muthén & Muthén, 2002). Kaplan (1995) describes

other approaches for estimating the power of tests for individual parameters in struc-

tural equation models.

An approach to power analysis at the model level by MacCallum, Browne, and Sug-

awara (1996) is based on the RMSEA and noncentral chi-square distributions for tests of

three different null hypotheses. Two of these hypotheses include the close-ﬁt hypothesis

: ε

≤ .05) and the exact-ﬁt hypothesis (H

: ε

= 0). The test of each hypothesis just

stated is an accept–support where low power favors the researcher’s model. The third

hypothesis is the not-close-ﬁt hypothesis, or H

: ε

≥ .05, which is an inversion of the

close-ﬁt hypothesis. If the upper bound of the 90% conﬁdence interval based on the

RMSEA is < .05, then the hypothesis that the model does not have close ﬁt in the popula-

tion is rejected. The test of the not-close-ﬁt hypothesis is a reject–support test, for which

low power works against the researcher’s model. This is because greater power here

implies a higher probability of detecting a reasonably correct model, or at least one that

implies a covariance matrix that approximates the sample data matrix. The accuracy of

tests for the close-ﬁt and not-close-ﬁt hypotheses assumes that the RMSEA actually fol-

lows a noncentral chi-square distribution.

A power analysis in the MacCallum et al. (1996) method for any of the null hypoth-

eses just described is conducted by specifying N, α, df

, and a suitable value of the

parameter estimated by the RMSEA under the alternative hypothesis H

, or ε

. For

example, ε

could be speciﬁed for the close-ﬁt hypothesis as .08, a suggested upper

threshold for reasonable approximation error. (But not a golden rule!) For the not-close-

ﬁt hypothesis, ε

could be speciﬁed as .01, which may represent the case of “good”

approximate ﬁt. A variation is to determine the minimum sample size needed to reach a

target level of power, such as .80, given α, df

, ε

, and ε

. The latter (ε

) is the “terminal

point” of the interval for the corresponding directional null hypothesis, which is ε

= .05

for both the close-ﬁt and not-hypotheses.

Estimated power or sample sizes can be obtained by consulting special tables in

MacCallum et al. (1996) or Hancock and Freeman (2001) for the not-close-ﬁt hypothesis

only or through use of a computer. In an appendix, MacCallum et al. (1996) give SAS/

STAT syntax for power analysis based on the methods just outlined. Friendly (2009)

describes a related SAS/STAT macro that carries out a MacCallum–Browne–Sugawara

power analysis that can be freely downloaded over the Internet.

A webpage by Preacher

and Coffman (2006) generates R code that conducts the same type of model-level power

analysis for a given model, calculates the minimum sample size required to obtain a tar-

get level of power, estimates power for testing differences between two nested models,