Кирюшин О.В. Управление техническими системами
Подождите немного. Документ загружается.


ss3s2
1s3s5,1
1s3s2
1
*
s
1s3s5,1
)s(W)s(W)s(W
23
2
2
2
oyp
,
откуда видно, что числитель В(s) = 1,5
.
s
2
+ 3
.
s + 1, знаменатель (он же
характеристический полином разомкнутой системы) А(s) = 2
.
s
3
+ 3
.
s
2
+ s. Тогда
характеристический полином замкнутой системы равен:
D(s) = A(s) + B(s) = 2
.
s
3
+ 3
.
s
2
+ s + 1,5
.
s
2
+ 3
.
s + 1 = 2
.
s
3
+ 4,5
.
s
2
+ 4
.
s + 1.
Передаточные функции замкнутой системы:
по заданию
1s4s5,4s2
1s3s5,1
)s(D
)s(B
)s(Ф
23
2
з
,
по ошибке
1s4s5,4s2
ss3s2
)s(D
)s(A
)s(Ф
23
23
e
.
При определении передаточной функции по возмущению принимается
W
у.в.
O=OW
оу
. Тогда
1s4s5,4s2
s
ss3s2
1s3s5,1
1
1s3s2
1
)s(W1
)s(W
)s(Ф
23
23
2
2
.в.у
в
.
2.6.5 Определение параметров передаточной функции
объекта по переходной кривой.
Процесс получения передаточной функции объекта, исходя из данных о
переходном процессе, называется идентификацией объекта.
Предположим, что при подаче на вход
некоторого объекта ступенчатого
воздействия была получена переходная
характеристика (см. рис. 1.31). Требуется
определить вид и параметры передаточной
функции.
Предположим, что передаточная функция
имеет вид
s
e
1Ts
K
)s(W
,
(инерционной звено с запаздыванием).
Параметры передаточной функции: К - коэффициент усиления, Т -
постоянная времени, - запаздывание.
Коэффициентом усиления называется величина, показывающая, во сколько
раз данное звено усиливает входной сигнал (в установившемся режиме),
и равна отношению выходной величины у в установившемся режиме ко
входной величине х:
х
у
K
уст
,
Установившееся значение выходной величины у
уст
- это значение у при
tOO.
31
у
у
уст
t
T
д
Рисунок 1.31
Запаздыванием называется промежуток времени от момента изменения
входной величины х до начала изменения выходной величины у.
Постоянная времени Т может быть определена несколькими методами в
зависимости от вида передаточной функции. Для рассматриваемой
передаточной функции 1-го порядка Т определяется наиболее просто:
сначала проводится касательная к точке перегиба, затем находятся точки
пересечения с осью времени и асимптотой y
уст
; время Т определяется как
интервал времени между этими точками.
В случае, если на графике между точкой перегиба имеется вогнутость,
определяется дополнительное запаздывание
доп
, которое прибавляется к
основному: = +
доп
.
2.7. Частотные характеристики.
2.7.1 Определение частотных характеристик.
Известно, что динамические процессы могут быть представлены
частотными характеристиками (ЧХ) путем разложения функции в ряд Фурье.
Предположим, имеется некоторый объект и требуется определить его
ЧХ. При экспериментальном снятии ЧХ на вход объекта подается
синусоидальный сигнал с амплитудой А
вх
= 1 и некоторой частотой , т.е.
x(t) = А
вх
sin(t) = sin(t).
Тогда после прохождения переходных
процессов на выходе мы будем также иметь
синусоидальный сигналтой же частоты , но
другой амплитуды А
вых
и фазы :
у(t) = А
вых
sin(t + )
При разных значениях величины А
вых
и , как правило, также будут
различными. Эта зависимость амплитуды и фазы от частоты называется
частотной характеристикой. Виды ЧХ:
АФХ – амплитудно-фазовая характеристика -
зависимость амплитуды и фазы выходного сигнала
от частоты входного (изображается на
комплексной плоскости);
АЧХ – амплитудно-частотная характеристика -
зависимость амплитуды выходного сигнала от
частоты входного: А();
ФЧХ – фазо-частотная характеристика -
зависимость фазы выходного сигнала от частоты
входного: () ;
ЛАХ, ЛАЧХ - логарифмические АЧХ, т.е.
построенные в логарифмических координатах..
На комплексной плоскости входная величина xOO=OА
вх
.
sin(t) для
каждого момента времени t
i
определяется вектором х на комплексной
32
х
у
Рисунок 1.32
Re
Im
t
x
y
Рисунок 1.33

плоскости. Этот вектор имеет длину, равную А
вх
, и отложен под углом t
i
к
действительной оси. (Re - действительная ось, Im - мнимая ось)
Тогда величину х можно записать в комплексной форме
x
(t) = А
вх
(cos(t) + j
.
sin(t)),
где j =
1
- мнимая единица.
Или, если использовать формулу Эйлера e
j
= cos + j
.
sin, то можно
записать
x
(t) = А
вх
.
e
j
t
.
Выходной сигнал y(t) можно аналогично представить как вектор
y
(t) = А
вых
.
e
j(
t+
)
.
Рассмотрим связь передаточной функции и частотной характеристики.
Определим производные по Лапласу:
у Y
у’ sY
у” s
2
Y и т.д.
Определим производные ЧХ:
у’(t) = j А
вых
е
j(
t +
)
= j у,
у”(t) = (j)
2
А
вых
е
j(
t +
)
= (j)
2
у и т.д.
Отсюда видно соответствие s = j.
Вывод: частотные характеристики могут быть построены по
передаточным функциям путем замены s = j.
Для построения АЧХ и ФЧХ используются формулы:
)(Im)(Re)(A
22
,
)Re(
)Im(
arctg)(
,
где Re() и Im() – соответственно вещественная и мнимая части выражения
для АФХ.
Формулы получения АФХ по АЧХ и ФЧХ:
Re() = A()
.
cos (), Im() = A()
.
sin ().
График АЧХ всегда расположен в одной четверти, т.к. частота > 0 и
амплитуда А > 0. График ФЧХ может располагаться в двух четвертях, т.е.
фаза может быть как положительной, так и отрицательной. График АФХ
может проходить по всем четвертям.
При графическом построении АЧХ по известной АФХ на кривой АФХ
выделяются несколько ключевых точек, соответствующих определенным
частотам. Далее измеряются расстояния от начала координат до каждой точки
и на графике АЧХ откладываются: по вертикали – измеренные расстояния, по
горизонтали – частоты. Построение АФХ производится аналогично, но
измеряются не расстояния, а углы в градусах или радианах.
Для графического построения АФХ необходимо знать вид АЧХ и ФЧХ.
При этом на АЧХ и ФЧХ выделяются несколько точек, соответствующих
33
некоторым частотам. Для каждой частоты по АЧХ определяется амплитуда А,
а по ФЧХ – фаза . Каждой частоте соответствует точка на АФХ, расстояние
до которой от начала координат равно А, а угол относительно положительной
полуоси Re равен . Отмеченные точки соединяются кривой.
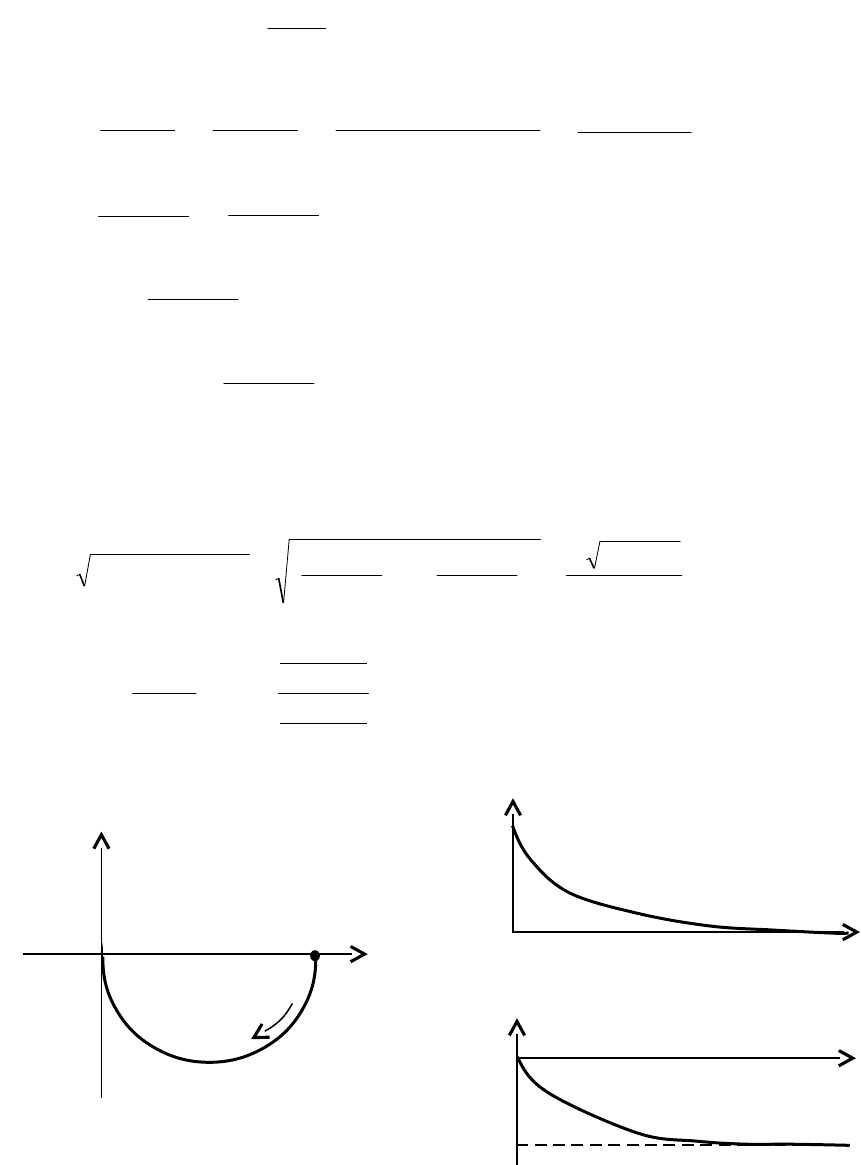
Пример:
1Ts
K
)s(W
.
При s = j имеем:
1Tj
K
)j(W
=
jT1
K
=
)jT1)(jT1(
)jT1(K
=
22
T1
KTjK
=
=
22
T1
K
- j
22
T1
KT
= Re() + j Im(),
т.е. Re() =
22
T1
K
- выражение для действительной части АФХ,
Im() =
22
T1
KT
- выражение для мнимой части АФХ (обратите
внимание, что в данном выражение мнимая единица j отсутствует).
Изменяя от 0 до , можно построить АФХ (см. рис. 1.34, а).
По формулам определяются выражения для АЧХ и ФЧХ:
22
22
2
22
2
22
22
T1
T1K
T1
KT
T1
K
)(Im)(Re)(A
,
)T(arctg
T1
K
T1
KT
arctg
)Re(
)Im(
arctg)(
22
22
.
Рисунок 1.34 – Примеры ЧХ
34
Re
Im
K
0
K
А
0
-90
а) АФХ
б) АЧХ
в) АФХ
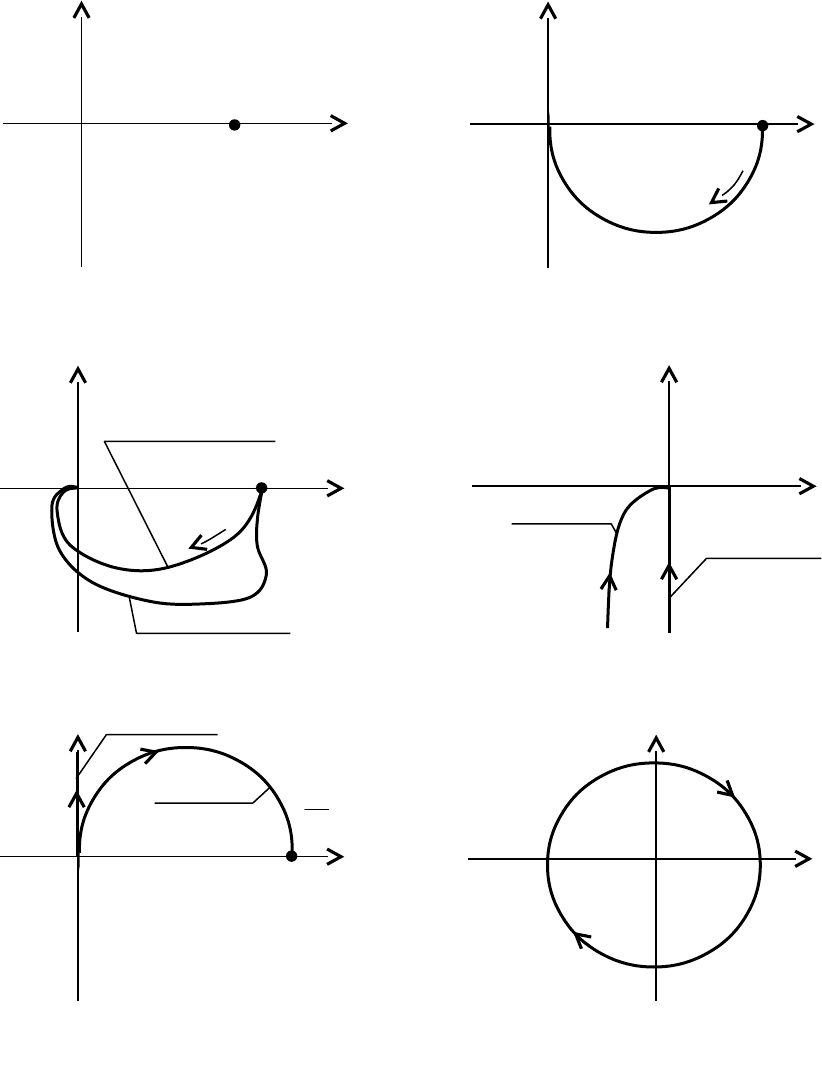
АЧХ и ФЧХ также строится путем изменения от 0 до (см. рис.
1.34,Oб и в).
На рисунке 1.35 изображены АФХ типовых звеньев, рассмотренных
ранее в п. 2.6.2.
Рисунок 1.35 – АФХ типовых звеньев
35
Re
Im
K
0
а) усилительное
Re
Im
K
0
б) инерционное
Re
Im
K
0
в) звенья 2-го порядка
Re
Im
K
0
г) интегрирующие
Re
Im
T
K
0
д) дифференцирующие
Re
Im
1
0
е) звено запаздывания
апериодическое
колебательное
идеальное
реальное
реальное
идеальное
-1
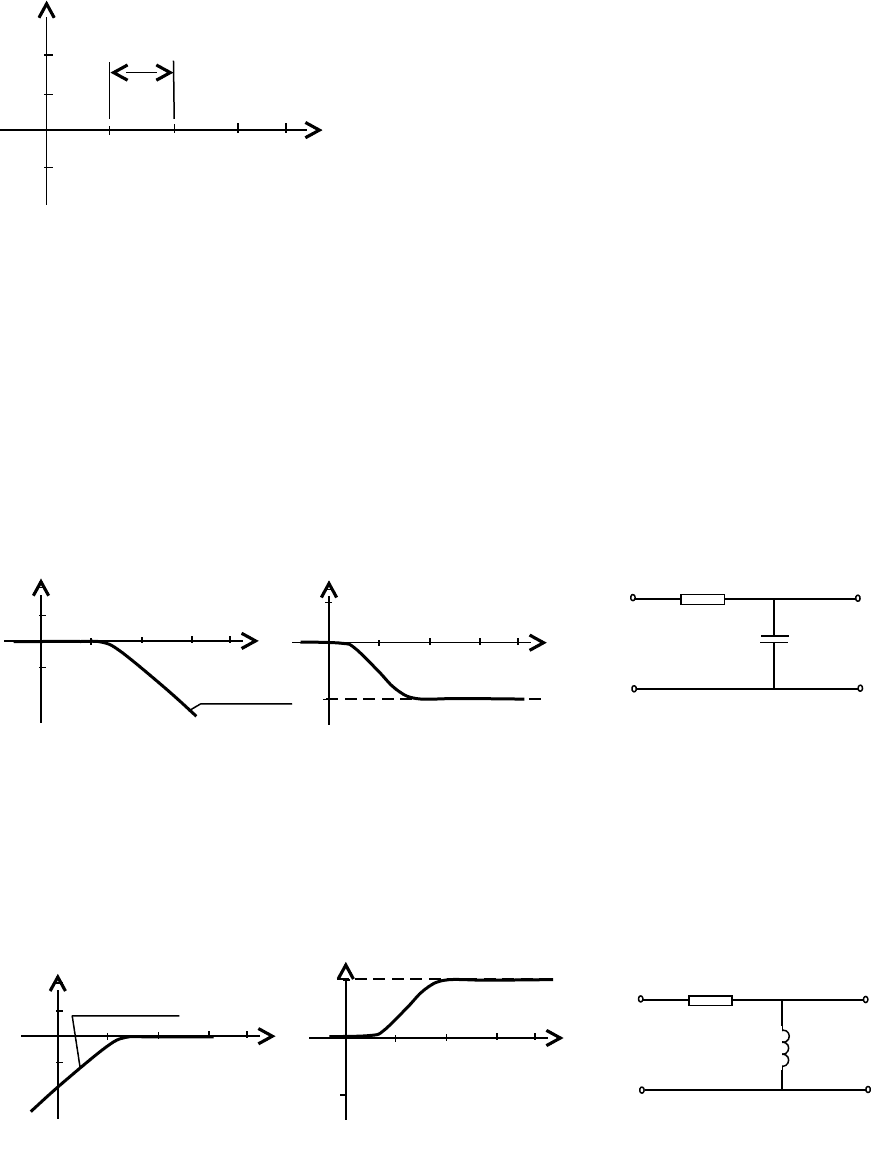
2.7.2 Логарифмические частотные характеристики.
Логарифмические частотные характеристики (ЛЧХ) используются
довольно часто для описания динамических параметров различных устройств.
Существуют два основных вида ЛЧХ, которые, как правило, используются
совместно и изображаются в виде графиков:
1) ЛАЧХ - логарифмическая АЧХ.
Формула для построения ЛАЧХ: L() = 20
.
lg
A
вых
().
Единица измерения - децибел (дБ).
На графике ЛАЧХ по оси абсцисс
откладывается частота в логарифмическом
масштабе. Это означает, что равным
величинам отрезков по оси соответствуют
кратные значения частоты. Для ЛЧХ
кратность = 10.
По оси ординат откладываются значения
L() в обычном масштабе.
2) ЛФЧХ - логарифмическая ФЧХ. Представляет из себя ФЧХ, у которой ось
частоты проградуирована в логарифмическом масштабе в
соответствии с ЛАЧХ. По оси ординат откладываются фазы .
Примеры ЛЧХ.
1. Фильтр низких частот (ФНЧ)
ЛАЧХ ЛФЧХ Пример цепи
Фильтр низких частот предназначен для подавления высокочастотных
воздействий.
2. Фильтр высоких частот (ФВЧ)
ЛАЧХ ЛФЧХ Пример цепи
36
L()
0,01
0,1
1
10
20
-20
декада
Рисунок 1.36
L()
0,01
0,1
1
10
20
-20
-20 дБ/дек
(),
0,01
0,1
1
10
90
-90
R
C
U
вх
U
вых
Рисунок 1.37
L()
0,01
0,1
1
10
20
-20
+20 дБ/дек
(),
0,01
0,1
1
10
90
-90
R
L
U
вх
U
вых
Рисунок 1.38
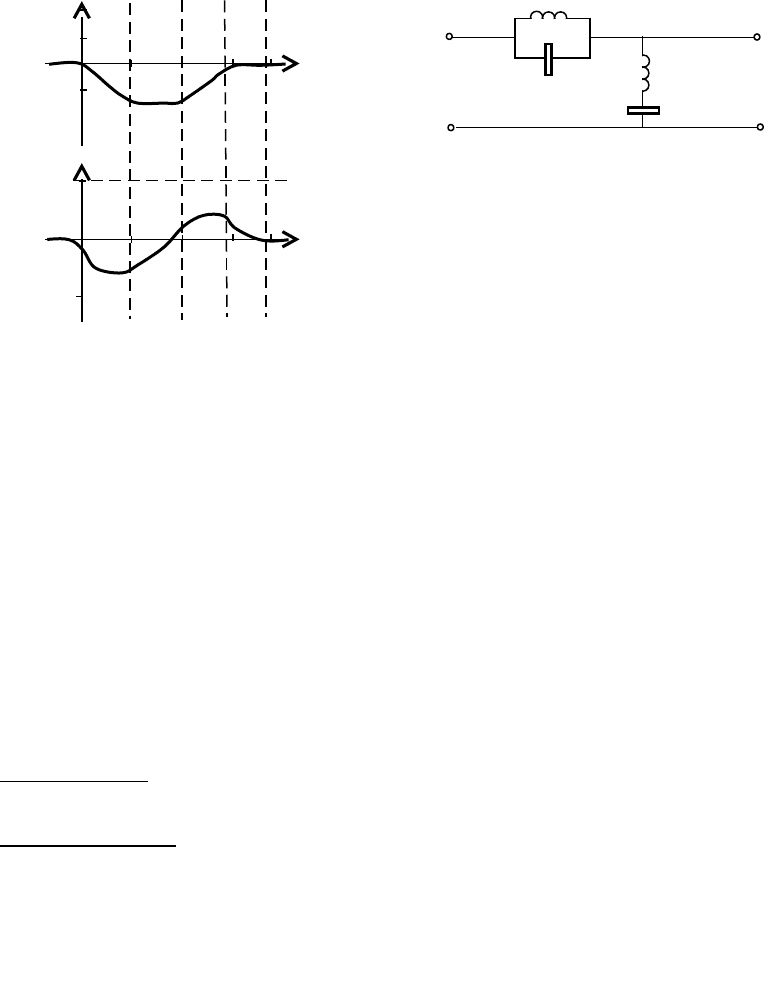
Фильтр высоких частот предназначен для подавления низкочастотных
воздействий.
3. Заградительный фильтр.
Заградительный фильтр подавляет только определенный диапазон
частот (см. рис. 1.39).
ЛАЧХ и ЛФЧХ Пример цепи
.
3. Качество процессов управления.
3.1. Критерии устойчивости.
3.1.1 Понятие устойчивости линейных систем.
Важным показателем АСР является устойчивость, поскольку основное
ее назначение заключается в поддержании заданного постоянного значения
регулируемого параметра или изменение его по определенному закону. При
отклонении регулируемого параметра от заданной величины (например, под
действием возмущения или изменения задания) регулятор воздействует на
систему таким образом, чтобы ликвидировать это отклонение. Если система в
результате этого воздействия возвращается в исходное состояние или
переходит в другое равновесное состояние, то такая система называется
устойчивой. Если же возникают колебания со все возрастающей амплитудой
или происходит монотонное увеличение ошибки е, то система называется
неустойчивой.
Необходимое и достаточное условие устойчивости формулируется
следующим образом: Звено или система называются устойчивыми, если
переходная составляющая с течением времени стремится к нулю:
0)t(ylim
п
t
.
Если выходной сигнал звена или системы y(t) рассматривать как сумму
двух составляющих
y(t) = y
уст
+ у
п
(t),
37
L()
0,01
0,1
1
10
20
-20
(),
0,01
0,1
1
10
90
-90
С
L
U
вх
U
вых
L
С
Рисунок 1.39
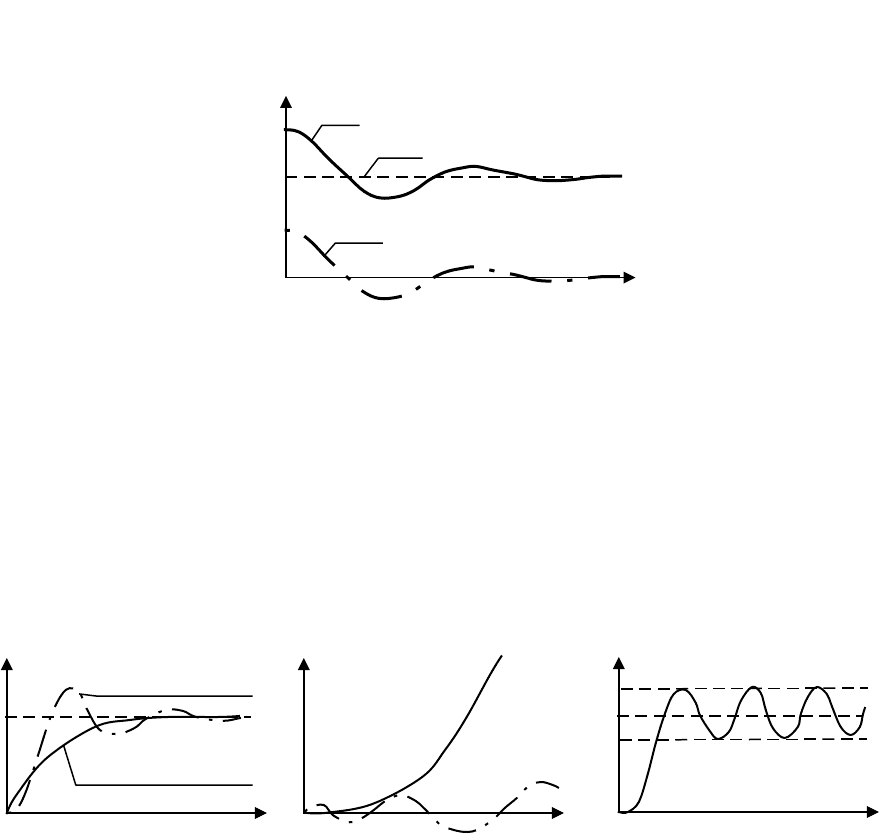
где
)t(ylimy
t
уст
- установившееся значение y(t), у
п
(t) – переходная
составляющая, то у
п
(t) = y(t) – y
уст
.
Рисунок 1.40
Если у
п
(t) с течением времени стремится к бесконечности, звено или
система называются неустойчивыми. Другими словами:
тиустойчивосграниценазвеносуществуетне
онеустойчивзвено
устойчивозвено0
)t(ylim
п
t
.
Примеры переходных процессов для каждого случая приведены на
рисунке 1.41.
Рисунок 1.41
Для того, чтобы определить, устойчива система или нет, используются
критерии устойчивости:
1) корневой критерий,
2) критерий Стодола,
3) критерий Гурвица,
4) критерий Найквиста,
5) критерий Михайлова и др.
Первые два критерия являются необходимыми критериями
устойчивости отдельных звеньев и разомкнутых систем, однако не являются
достаточными для однозначного определения устойчивости.
Критерий Гурвица является алгебраическим и может быть использован
для определения устойчивости как отдельных звеньев, так и замкнутых
систем без запаздывания. При этом он позволяет обойтись без определения
38
колебательный
процесс
апериодический
устойчивые процессы
t
у
неустойчивые процессы
t
у
на границе устойчивости
t
у
y(t)
y
п
(t)
y
уст
y
t

корней характеристического полинома, который может иметь достаточно
большую степень.
Последние два критерия относятся к группе частотных критериев,
поскольку определяют устойчивость замкнутых систем по их частотным
характеристикам. Их особенностью является возможность применения к
замкнутым системам с запаздыванием, которыми является подавляющее
большинство систем управления.
3.1.2 Корневой критерий.
Функция y
п
(t) является решением однородного дифференциального
уравнения, поэтому устойчивость системы однозначно зависит от корней
характеристического уравнения.
Если корни действительные, т.е. s
i
=
i
, то
n
1i
ts
iп
i
eM)t(y
,
где n – число корней характеристического уравнения (степень уравнения),
M
i
O–Oкоэффициенты, s
i
– корни.
Каждая составляющая функции y
п
(t) является экспонентой вида
ts
ii.п
i
eM)t(y
.
При этом если s
i
> 0, то экспонента расходится (
)t(ylim
п
t
), если s
i
< 0
- сходится (
0)t(ylim
п
t
).
В случае, если среди корней характеристического уравнения имеются
комплексные, т.е. s
i
=
i
j
i
, то каждой паре комплексно сопряженных
корней соответствует составляющая
)]tsin(d)tcos(c[e2)t(y
iiii
t
i.п
i
,
где c
i
и d
i
– коэффициенты. Данная составляющая представляет собой
синусоиду, сходящуюся при
i
< 0 и расходящуюся при
i
> 0 (при
i
= 0
синусоида имеет постоянную амплитуду).
Для устойчивости системы необходимо и достаточно, чтобы все
составляющие функции y
п.i
(t) стремились с течением времени к нулю. Если
хотя бы одна составляющая функции расходится, то расходится и вся
функция, т.е. система в данном случае неустойчива.
Из сказанного следует, что для устойчивости линейной системы
необходимо и достаточно, чтобы корни характеристического полинома имели
отрицательные действительные части.
Критерий, определяющий устойчивость системы по значениям корней
характеристического полинома, получил название корневого.
Для определения устойчивости необходимо путем приравнивания
знаменателя передаточной функции (характеристического полинома) к нулю
получить характеристическое уравнение и его корни. Корни
характеристического уравнения могут быть как действительные, так и
комплексные и для наглядности могут быть изображены на комплексной
плоскости (плоскости корней).
39
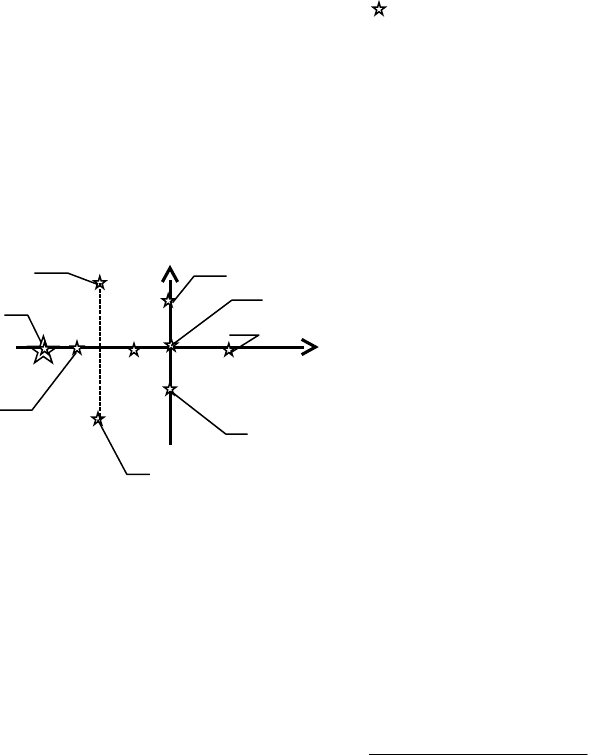
На рисунке 1.42 символом обозначены корни некоторого уравнения.
Виды корней характеристического уравнения:
- действительные: положительные (корень 1), отрицательные (корень 2) и
нулевые (корень 3);
- комплексные: комплексные сопряженные (4) и чисто мнимые (5).
По кратности корни бывают: одиночные (1, 2, 3), сопряженные (4, 5):
s
iO
=OOOj и кратные (6) s
i
= s
i+1
= …
Корневой критерий формулируется следующим образом:
Линейная АСР устойчива, если все корни
характеристического уравнения лежат в
левой полуплоскости (она называется также
областью устойчивости). Если хотя бы один
корень находится на мнимой оси, которая
является границей устойчивости, то говорят,
что система находится на границе
устойчивости. Если хотя бы один корень
находится в правой полуплоскости (не
зависимо от числа корней в левой), то
система является неустойчивой.
Иными словами, все действительные корни и действительные части
комплексных корней должны быть отрицательны. В противном случае
система неустойчива.
Пример. Передаточная функция системы имеет вид:
25.1s25.2s2s
4s3
)s(W
23
.
Характеристическое уравнение: s
3
+ 2s
2
+ 2,25s + 1.25 = 0 имеет три корня:
s
1
= -1; s
2
= -0,5 + j; s
3
= -0,5 - j.
Действительные части всех корней отрицательны, следовательно, система
устойчива.
3.1.3 Критерий Стодолы.
Этот критерий является следствием из предыдущего и формулируется
следующим образом: Линейная система устойчива, если все коэффициенты
характеристического полинома положительны.
То есть, передаточная функция из примера по критерию Стодола
соответствует устойчивой системе.
3.1.4 Критерий Гурвица.
Критерий Гурвица, как и критерий Стодола, определяет устойчивость
по характеристическому полиному системы без непосредственного
вычисления его корней. Однако критерий Стодола является необходимым
критерием устойчивости, но не является достаточным. То есть, если по
критерию Стодола система неустойчива, то она действительно является
неустойчивой, если по критерию система устойчива, то для подтверждения ее
40
Re
Im
0
3
2
1
5
5
4
4
6
Рисунок 1.42
