Кирюшин О.В. Управление техническими системами
Подождите немного. Документ загружается.

числителя исходной определяется система из n уравнений, где n – степень
знаменателя (количество корней s
i
и коэффициентов M
i
). Решение системы
относительно M
i
дает искомые коэффициенты.
Пример. Декомпозиция дроби из предыдущего примера. В исходной
дроби n = 3, поэтому решение уравнения s
3
+ 5s
2
+ 6s = 0 дает 3 корня: s
0
= 0,
s
1
O=O-2 и s
2
= -3, которым соответствуют знаменатели простых дробей вида s,
(sO–Os
1
) = (s + 2) и (sO–Os
2
) = (s + 3). Исходная дробь декомпозируется на три
дроби:
s6s5s
12s2
Y
23
=
)3s)(2s(s
12s2
=
s
M
0
+
2s
M
1
+
3s
M
2
.
Далее дроби приводятся к общему знаменателю:
=
)3s)(2s(s
M6s)M2M3M5(s)MMM(
0210
2
210
.
Сравнивая получившуюся дробь с исходной, можно составить систему
из трех уравнений с тремя неизвестными (при 2-й степени s в исходной дроби
стоит 0, при 1-й стоит 2, свободный член равен 12):
М
0
+ М
1
+ М
2
= 0 M
0
= 2
5
.
М
0
+ 3
.
М
1
+ 2
.
М
2
= 2 M
1
= -4
6
.
М
0
= 12 M
2
= 2
Следовательно, дробь можно представить как сумму трех дробей:
s6s5s
12s2
Y
23
=
s
2
-
2s
4
+
3s
2
.
Второй вариант. Определение коэффициентов M
i
по формулам.
Также как и в 1-м варианте необходимо найти корни знаменателя
исходной дроби вида
)s(A
)s(B
)s(Y
. Для определения M
i
существуют формулы
для каждого вида корней:
- Для нулевого корня s
i
= 0 знаменатель исходной дроби можно записать в
виде A(s) = s
.
A
1
(s); тогда коэффициент M
i
можно определить как
0s
1
i
)s(A
)s(B
M
.
- Для ненулевого некратного корня (действительного или комплексного) s
i
:
i
ss
i
)s('A
)s(B
M
,
где A’(s) – производная знаменателя по s.
Примечание: Комплексные корни при решении уравнений появляются
комплексно-сопряженными парами вида s
i
=
i
j
i
, где
i
–
действительныя часть корня,
i
– мнимая часть, j – мнимая единица.
Поэтому коэффициенты для этих корней также будут комплексно-
сопряженными: M
i
= c
i
d
i
. То есть достаточно определить
21

коэффициент только для одного корня, для парного корня он будет
комплексно-сопряженным.
- Для корня s
i
кратности k исходная дробь может быть представлена в виде
)s(A)ss(
)s(B
)s(A
)s(B
)s(Y
1
k
i
;
данному корню соответствуют k дробей вида
k,1j,
)ss(
M
j1k
i
ij
,
коэффициенты которых определяются по формуле
)s(A
)s(B
ds
d
lim
)!1j(
1
M
1
1j
1j
ss
k,1j
j1k,i
i
.
Пример. Декомпозиция дроби. Рассматривается та же дробь, имеющая
три корня: s
0
= 0, s
1
O=O-2 и s
2
= -3.
Для корня s
0
= 0 имеем B(s) = 2
.
s + 12, A
1
(s) = s
2
+ 5s + 6 ,
2
6
12
6s5s
12s2
)s(A
)s(B
M
0s
2
0s
1
0
.
Для корня s
1
= -2 имеем A’(s) = 3
.
s
2
+ 10
.
s + 6 и
4
2
8
6s10s3
12s2
)s('A
)s(B
M
2s
2
ss
1
1
.
Для корня s
2
= -3 имеем аналогично
2
3
6
6s10s3
12s2
)s('A
)s(B
M
3s
2
ss
2
21
.
Видно, что коэффициенты M
i
, полученные разными методами, совпадают.
Пример. Случай обратного преобразования Лапласа при наличии
комплексных корней.
Изображение выходного сигнала имеет вид:
)75,6s3,4s22,5s8,1(s
75,5
)s(Y
23
.
Корни знаменателя включают нулевой корень, действительный и пару
комплексных корней: s
0
= 0; s
1
= - 2,54; s
2,3
= - 0,18 j*1,20.
Изображение Y(s) разбивается на сумму четырех дробей:
3
3
2
2
1
1
0
3,210
ss
M
ss
M
ss
M
s
M
)s(Y)s(Y)s(Y)s(Y
.
Тогда оригинал y(t), согласно табл. 1.1 и 1.2, имеет вид:
y(t) = y
0
(t) + y
1
(t) + y
2,3
(t) = M
0
+
tS
1
1
e*M
+ 2 е
t
[C
.
cos(
.
t) - D
.
sin(
.
t)],
где и - действительная и мнимая части пары комплексных корней s
2,3
, C и
D – действительная и мнимая части пары коэффициентов М
2
и М
3
.
Для корня s
0
= 0:
85,0
75,6
75,5
75,6s3,4s22,5s8,1
75,5
)0(A
)0(B
M
0S
23
1
0
,
s
85,0
s
M
)s(Y
0
0
,
22

y
0
(t) = M
0
= 0,85;
Для корня s
1
= -2,54:
1SS
234
1SS
'
1
)'s75,6s3,4s22,5s8,1(
75,5
)s(A
)s(B
M
,
18,0
75,6s6,8s66,15s2,7
75,5
1SS
23
,
54,2s
18,0
ss
M
)s(Y
1
1
1
,
y
1
(t) =
t54,2
tS
1
e*18,0e*M
1
;
в) для корней s
2,3
= -0,18 j*1,20:
2SS
234
2SS
'
2
)'s75,6s3,4s22,5s8,1(
75,5
)s(A
)s(B
M
,
24,0*j34,0
75,6s6,8s66,15s2,7
75,5
2SS
23
,
20,1j18,0s
24,0j34,0
20,1j18,0s
24,0j34,0
ss
M
ss
M
)s(Y
3
3
2
2
3,2
,
y
2,3
(t) =2 е
-0,18t
[-0,34 cos(1,20 t) - 0,24 sin(1,20 t)].
В итоге получаем оригинал:
y(t) = 0,85 – 0,18 е
-2,54 t
– 2 е
-0,18 t
[0,34 cos(1,20 t) + 0,24 sin(1,20 t)].
2.6. Передаточные функции.
2.6.1 Определение передаточной функции.
Преобразование ДУ по Лапласу дает возможность ввести удобное
понятие передаточной функции, характеризующей динамические свойства
системы.
Например, операторное уравнение
3s
2
Y(s) + 4sY(s) + Y(s) = 2sX(s) + 4X(s)
можно преобразовать, вынеся X(s) и Y(s) за скобки и поделив друг на друга:
Y(s)*(3s
2
+ 4s + 1) = X(s)*(2s + 4)
1s4s3
4s2
)s(X
)s(Y
)s(W
2
.
Полученное выражение называется передаточной функцией.
Передаточной функцией называется отношение изображения выходного
воздействия Y(s) к изображению входного X(s) при нулевых начальных
условиях.
)s(X
)s(Y
)s(W
(2.4)
Передаточная функция является дробно-рациональной функцией
комплексной переменной:
n
n
2
210
m
m
2
210
sa...sasaa
sb...sbsbb
)s(A
)s(B
)s(W
,
23

где B(s) = b
0
+ b
1
s + b
2
s
2
+ … + b
m
s
m
- полином числителя,
А(s) = a
0
+ a
1
s + a
2
s
2
+ … + a
n
s
n
- полином знаменателя.
Передаточная функция имеет порядок, который определяется порядком
полинома знаменателя (n).
Из (2.4) следует, что изображение выходного сигнала можно найти как
Y(s) = W(s)*X(s).
Так как передаточная функция системы полностью определяет ее
динамические свойства, то первоначальная задача расчета АСР сводится к
определению ее передаточной функции.
2.6.2 Примеры типовых звеньев.
Звеном системы называется ее элемент, обладающий определенными
свойствами в динамическом отношении. Звенья систем регулирования могут
иметь разную физическую природу (электрические, пневматические,
механические и др. звенья), но описываться одинаковыми ДУ, а соотношение
входных и выходных сигналов в звеньях описываться одинаковыми
передаточными функциями.
В ТАУ выделяют группу простейших звеньев, которые принято
называть типовыми. Статические и динамические характеристики типовых
звеньев изучены достаточно полно. Типовые звенья широко используются при
определении динамических характеристик объектов управления. Например,
зная переходную характеристику, построенную с помощью самопишущего
прибора, часто можно определить, к какому типу звеньев относится объект
управления, а, следовательно, его передаточную функцию, дифференциальное
уравнение и т.д., т.е. модель объекта. Типовые звенья Любое сложное звено
может быть представлено как соединение простейших звеньев.
К простейшим типовым звеньям относятся:
усилительное,
инерционное (апериодическое 1-го порядка),
интегрирующие (реальное и идеальное),
дифференцирующие (реальное и идеальное),
апериодическое 2-го порядка,
колебательное,
запаздывающее.
1) Усилительное звено.
Звено усиливает входной сигнал в К раз. Уравнение
звена у = К*х, передаточная функция W(s) = К.
Параметр К называется коэффициентом усиления.
Выходной сигнал такого звена в точности повторяет
входной сигнал, усиленный в К раз (см. рис. 1.18).
у = K
.
x.
При ступенчатом воздействии h(t) = K.
24
К
у
t
Рисунок 1.18

Примерами таких звеньев являются: механические
передачи, датчики, безынерционные усилители и др.
2) Интегрирующее.
2.1) Идеальное интегрирующее.
Выходная величина идеального интегрирующего звена
пропорциональна интегралу входной величины.
t
0
dt)t(xKy
; W(s) =
s
K
При подаче на вход звена ступенчатого воздействия
x(t)O=O1 выходной сигнал постоянно возрастает (см.
рис. 1.19)
h(t) = K
.
t.
Это звено астатическое, т.е. не имеет установившегося режима.
Примером такого звена может служить емкость, наполняемая
жидкостью. Входной параметр – расход поступающей жидкости, выходной -
уровень. Изначально емкость пуста и при отсутствии расхода уровень равен
нулю, но если включить подачу жидкости, уровень начинает равномерно
увеличиваться.
2.2) Реальное интегрирующее.
Передаточная функция этого звена имеет вид:
W(s) =
)1Ts(s
K
.
Переходная характеристика в отличие от идеального
звена является кривой (см. рис. 1.20):
h(t) = K
.
(t – T) + K
.
T
.
e
-t/T
.
Примером интегрирующего звена является двигатель постоянного тока
с независимым возбуждением, если в качестве входного воздействия принять
напряжение питания статора, а выходного - угол поворота ротора. Если
напряжение на двигатель не подается, то ротор не двигается и угол его
поворота можно принять равным нулю. При подаче напряжения ротор
начинает раскручиваться, а угол его поворота сначала медленно вследствие
инерции, а затем быстрее увеличиваться до достижения определенной
скорости вращения.
3) Дифференцирующее.
3.1) Идеальное дифференцирующее.
Выходная величина пропорциональна производной по времени от
входной:
dt
)t(dx
Ky
; W(s) = K*s
25
у
t
Рисунок 1.20
Т
= arctg K
у
t
Рисунок 1.19
= arctg K

При ступенчатом входном сигнале выходной сигнал представляет собой
импульс (-функцию): h(t) = K
.
(t).
3.2) Реальное дифференцирующее.
Идеальные дифференцирующие звенья
физически не реализуемы. Большинство объектов,
которые представляют собой дифференцирующие
звенья, относятся к реальным дифференцирующим
звеньям, передаточные функции которых вид:
W(s) =
1Ts
Ks
.
Переходная характеристика:
T
t
e
T
K
)t(h
.
Пример звена: электрогенератор. Входной параметр – угол поворота
ротора, выходной – напряжение. Если ротор повернуть на некоторый угол, то
на клеммах появится напряжение, но если ротор далее не вращать,
напряжение снизится до нуля. Резко упасть оно не может вследствие наличия
индуктивности у обмотки.
4) Апериодическое (инерционное).
Этому звену соответствуют ДУ и ПФ вида:
Kxy
dt
dy
T
; W(s) =
1Ts
K
.
Определим характер изменения выходной величины этого звена при
подаче на вход ступенчатого воздействия величины х
0
.
Изображение ступенчатого воздействия: X(s) =
s
x
0
. Тогда изображение
выходной величины:
Y(s) = W(s) X(s) =
1Ts
K
s
x
0
= K x
0
)1Ts(s
1
.
Разложим дробь на простые:
)1Ts(s
1
=
1Ts
A
+
s
B
=
)1Ts(s
BBTsAs
=
s
1
-
1Ts
T
=
s
1
-
T
1
s
1
Оригинал первой дроби по таблице: L
-1
{
s
1
} = 1, второй:
L
-1
{
T
1
s
1
} =
T
t
e
.
Тогда окончательно получаем:
y(t) = K x
0
(1 -
T
t
e
).
Постоянная Т называется постоянной времени.
Большинство тепловых объектов являются
апериодическими звеньями. Например, при
подаче на вход электрической печи напряжения
26
у
t
К
Рисунок 1.22
Т
К
у
t
Рисунок 1.21
Т

ее температура будет изменяться по
аналогичному закону (см. рис. 1.22).
5) Звенья второго порядка
Звенья имеют ДУ и ПФ вида
Kxy
dt
dy
T
dt
yd
T
1
2
2
2
2
,
W(s) =
1sTsT
K
1
22
2
.
При подаче на вход ступенчатого
воздействия амплитудой х
0
на
переходная кривая будет иметь один из
двух видов: апериодический (при Т
1
2Т
2
) или колебательный (при Т
1
OO<O2Т
2
).
В связи с этим выделяют звенья второго порядка:
апериодическое 2-го порядка (Т
1
2Т
2
),
инерционное (Т
1
OO<O2Т
2
),
консервативное (Т
1
= 0).
6) Запаздывающее.
Если при подаче на вход объекта некоторого сигнала он реагирует на
этот сигнал не моментально, а спустя некоторое время, то говорят, что объект
обладает запаздыванием.
Запаздывание – это интервал времени от момента изменения входного
сигнала до начала изменения выходного.
Запаздывающее звено – это звено, у которого выходная величина у в
точности повторяет входную величину х с некоторым запаздыванием :
y(t) = x(t - ).
Передаточная функция звена:
W(s) = e
-
s
.
Примеры запаздываний: движение жидкости по трубопроводу (сколько
жидкости было закачано в начале трубопровода, столько ее выйдет в конце,
но через некоторое время, пока жидкость движется по трубе), движение груза
по конвейеру (запаздывание определяется длиной конвейера и скоростью
движения ленты) и т.д..
2.6.3 Соединения звеньев.
Поскольку исследуемый объект в целях упрощения анализа
функционирования разбит нами на звенья, то после определения
передаточных функций для каждого звена встает задача объединения их в
одну передаточную функцию объекта. Вид передаточной функции объекта
зависит от последовательности соединения звеньев:
1) Последовательное соединение.
W
об
= W
1
.
W
2
.
W
3
…
27
y
t
K
.
x
0
T
1
< 2T
2
T
1
2T
2
Рисунок 1.23
W
1
W
2
W
3
х
у
Рисунок 1.24
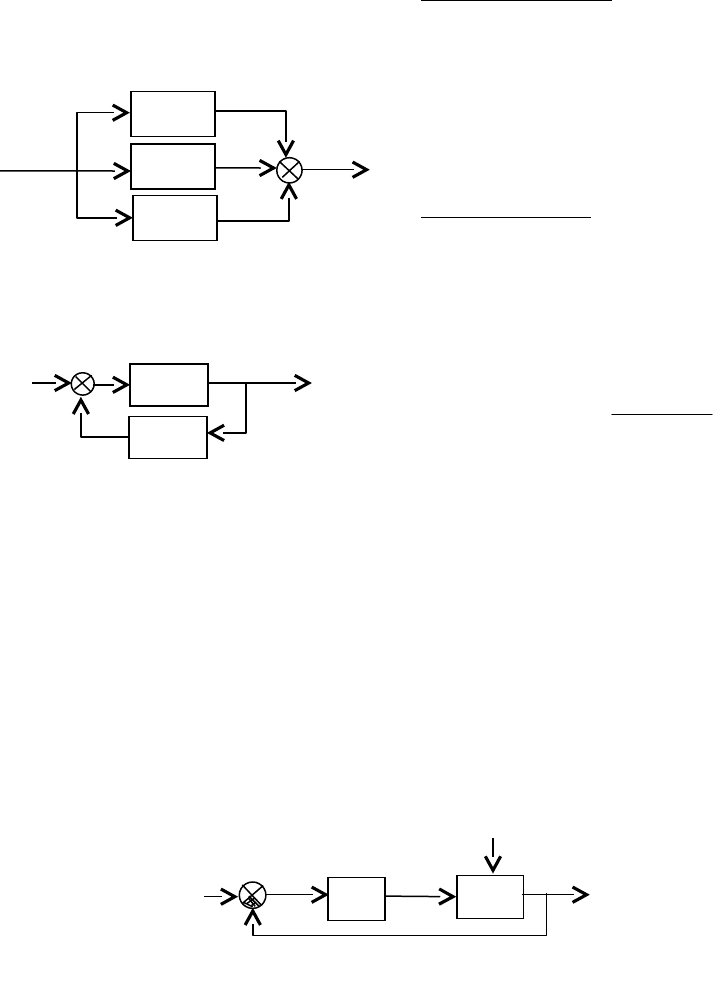
При последовательном соединении
звеньев их передаточные функции
перемножаются.
2) Параллельное соединение.
W
об
= W
1
+ W
2
+ W
3
+ …
При параллельном соединении
звеньев их передаточные функции
складываются.
3) Обратная связь
Передаточная функция по заданию (х):
21
1
ç
WW1
W
)s(W
«+» соответствует отрицательной ОС,
«-» - положительной.
Для определения передаточных функций объектов, имеющих более
сложные соединения звеньев, используют либо последовательное укрупнение
схемы, либо преобразуют по формуле Мезона [26].
2.6.4 Передаточные функции АСР.
Для исследования и расчета структурную схему АСР путем
эквивалентных преобразований приводят к простейшему стандартному виду
«объект - регулятор» (см. рисунок 1.27). Практически все инженерные методы
расчета и определения параметров настройки регуляторов применены для
такой стандартной структуры.
В общем случае любая одномерная АСР с главной обратной связью
путем постепенного укрупнения звеньев может быть приведена к такому
виду.
Если выход системы у не подавать на ее вход, то получается
разомкнутая система регулирования, передаточная функция которой
определяется как произведение:
W
= W
p
.
W
y
(W
p
- ПФ регулятора, W
y
- ПФ объекта управления).
28
W
1
W
2
W
3
х
у
Рисунок 1.25
W
1
W
2
х у
Рисунок 1.26
W
p
W
y
x
e
u
y
f
Рисунок 1.27

То есть последовательность звеньев W
p
и W
y
может быть заменена одним звеном с W
.
Передаточную функцию замкнутой системы
принято обозначать как Ф(s). Она может быть
выражена через W
:
Ф
з
(s) =
)s(X
)s(Y
=
)s(W1
)s(W
.
(далее будем рассматривать только системы с обратной отрицательной
связью, поскольку они используются в подавляющем большинстве АСР).
Данная передаточная функция Ф
з
(s) определяет зависимость у от х и
называется передаточной функцией замкнутой системы по каналу задающего
воздействия (по заданию).
Для АСР существуют также передаточные функции по другим каналам:
Ф
e
(s) =
)s(X
)s(E
=
)s(W1
1
- по ошибке,
Ф
в
(s) =
)s(F
)s(Y
=
)s(W1
)s(W
.в.у
- по возмущению,
где W
у.в.
(s) – передаточная функция объекта управления по каналу передачи
возмущающего воздействия.
В отношении учета возмущения возможны два варианта:
- возмущение оказывает аддитивное влияние на управляющее воздействие
(см. рис. 1.29,а);
- возмущение влияет на измерения регулируемого параметра (см. рис.O1.29,б).
Примером первого варианта может быть влияние колебаний
напряжения в сети на напряжение, подаваемое регулятором на
нагревательный элемент объекта. Пример второго варианта: погрешности при
измерениях регулируемого параметра вследствие изменения температуры
окружающей среды. W
у.в.
– модель влияния окружающей среды на измерения.
а) б)
Рисунок 1.29
Для первого варианта передаточная функция W
у.в.
принимается равной
W
у
, для второго – как правило, на схеме она выделена в отдельное звено.
Поскольку передаточная функция разомкнутой системы является в
общем случае дробно-рациональной функцией вида W
=
)s(A
)s(B
, то
передаточные функции замкнутой системы могут быть преобразованы:
29
W
х
у
Рисунок 1.28
W
p
W
y
x
e
u
y
f
W
p
W
y
x
e
u
y
f
W
y.в.
Ф
з
(s) =
A
B
1
A
B
=
BA
B
=
D
B
, Ф
e
(s) =
A
B
1
1
=
BA
A
=
D
A
,
где D = A + B.
Как видно, эти передаточные функции отличаются только выражениями
числителей. Выражение знаменателя называется характеристическим
выражением замкнутой системы и обозначается как D
з
(s) = A(s) + B(s), в то
время как выражение, находящееся в знаменателе передаточной функции
разомкнутой системы W
, называется характеристическим выражением
разомкнутой системы А(s).
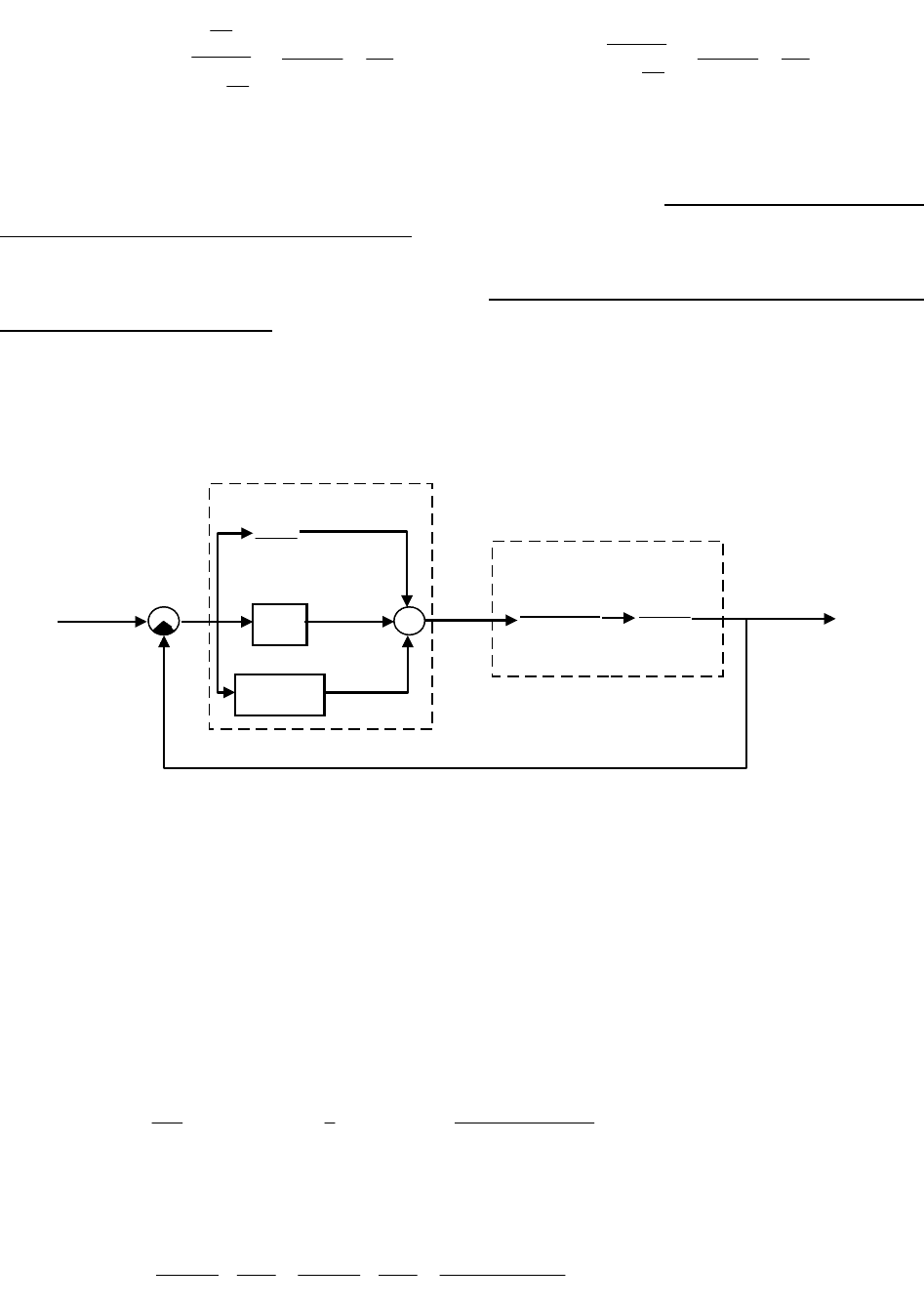
Пример. Определение передаточных функций АСР.
Структура АСР представлена на рисунке 1.30. Требуется определить
передаточные функции регулятора, объекта, разомкнутой системы, замкнутой
системы и характеристические выражения.
Рисунок 1.30
Параметры K
0
= 1, K
1
= 3, K
2
= 1,5, K
4
= 2, K
5
= 0,5.
В структурной схеме АСР звенья, соответствующие регулирующему
устройству, стоят перед звеньями объекта управления и генерируют
управляющее воздействие на объект u. По схеме видно, что к схеме
регулятора относятся звенья 1, 2 и 3, а к схеме объекта – звенья 4 и 5.
Учитывая, что звенья 1, 2 и 3 соединены параллельно, получаем
передаточную функцию регулятора как сумму передаточных функций
звеньев:
s
1s3s5,1
s5,13
s
1
sKK
s
K
)s(W
2
21
0
p
.
Звенья 4 и 5 соединены последовательно, поэтому передаточная
функция объекта управления определяется как произведение передаточных
функций звеньев:
1s3s2
1
1s
5,0
*
1s2
2
1s
K
*
1s2
K
)s(W
2
5
4
oy
.
Передаточная функция разомкнутой системы:
30
s
K
0
K
1
K
2
s
1s2
K
4
x
u
y
e
1
2
3
4
1s
K
5
5
Объект управления
Регулятор
