Казаринов Л.С., Попова О.В., Барбасова Т.А. Автоматизированные информационно-управляющие системы (часть 2)

Подождите немного. Документ загружается.

где U, U

– функции полезности, изменяющиеся от 0 до 1; w

– коэффициенты

важности (веса) критериев, причем 0<w

<1; коэффициент k>-1. Таким

образом, многокритериальную функцию полезности можно определить, если

известны значения коэффициентов w

, k , а также однокритериальные

функции полезности U

(х).

Полученный теоретический результат является основой метода,

неоднократно использованного для решения практических задач. Обсудим

приведенные выше этапы применения этого метода, используя в качестве

примера задачу выбора площадки для строительства аэропорта.

Построение однокритериальных функций полезности

Предположим, что после рассмотрения вариантов разброс оценок по

критериям может быть представлен таблице 4.8.

Зная диапазон изменения оценок по каждому из критериев, построим

функцию, определяющую полезность для ЛПР каждой оценки из этого

диапазона. Максимальное значение этой функции положим равным единицы,

а минимальное - нулю.

Таблица 4.8

Разброс оценок вариантов постройки аэропорта

Критерий

Наихудше

е значение

Наилучшее

значение

) Стоимость постройки аэропорта

$ 200 млн $ 100 млн

(С

) Время поездки от центра города

90 мин

40 мин

(С

) Количество людей, подвергающихся

шумовым воздействиям

50 тыс. 5 тыс.

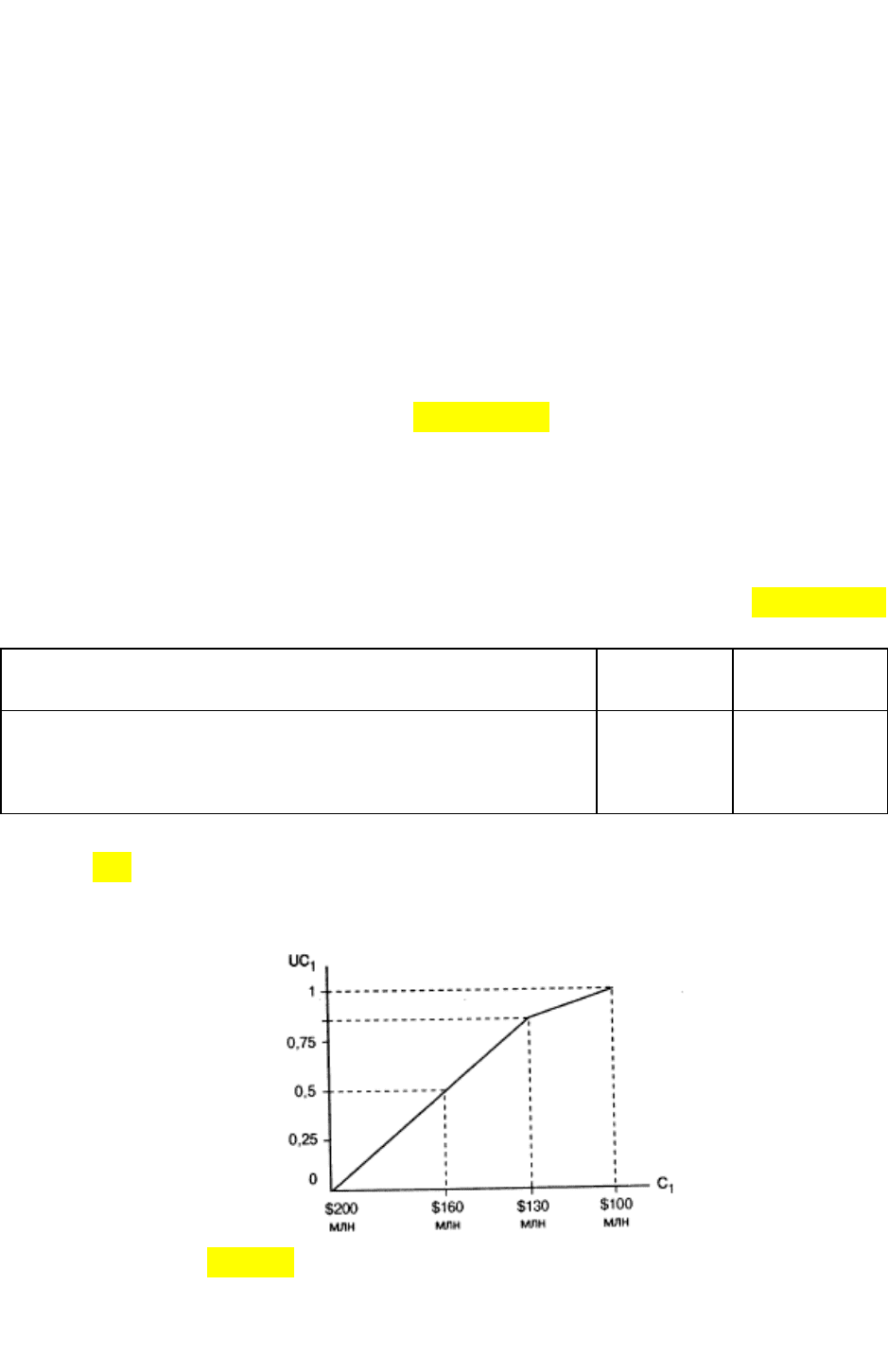
На рис. 4.9 приведен пример построения функции полезности ЛПР для

критерия «Стоимость постройки аэропорта».

Рис. 4.9. Функция полезности для критерия С

Первоначально известны две точки функции полезности: U($100 млн)=1,

U($200 млн)=0. Для нахождения промежуточных точек используются

типовые лотереи. Лотереей называется игра с двумя исходами: исходом х,

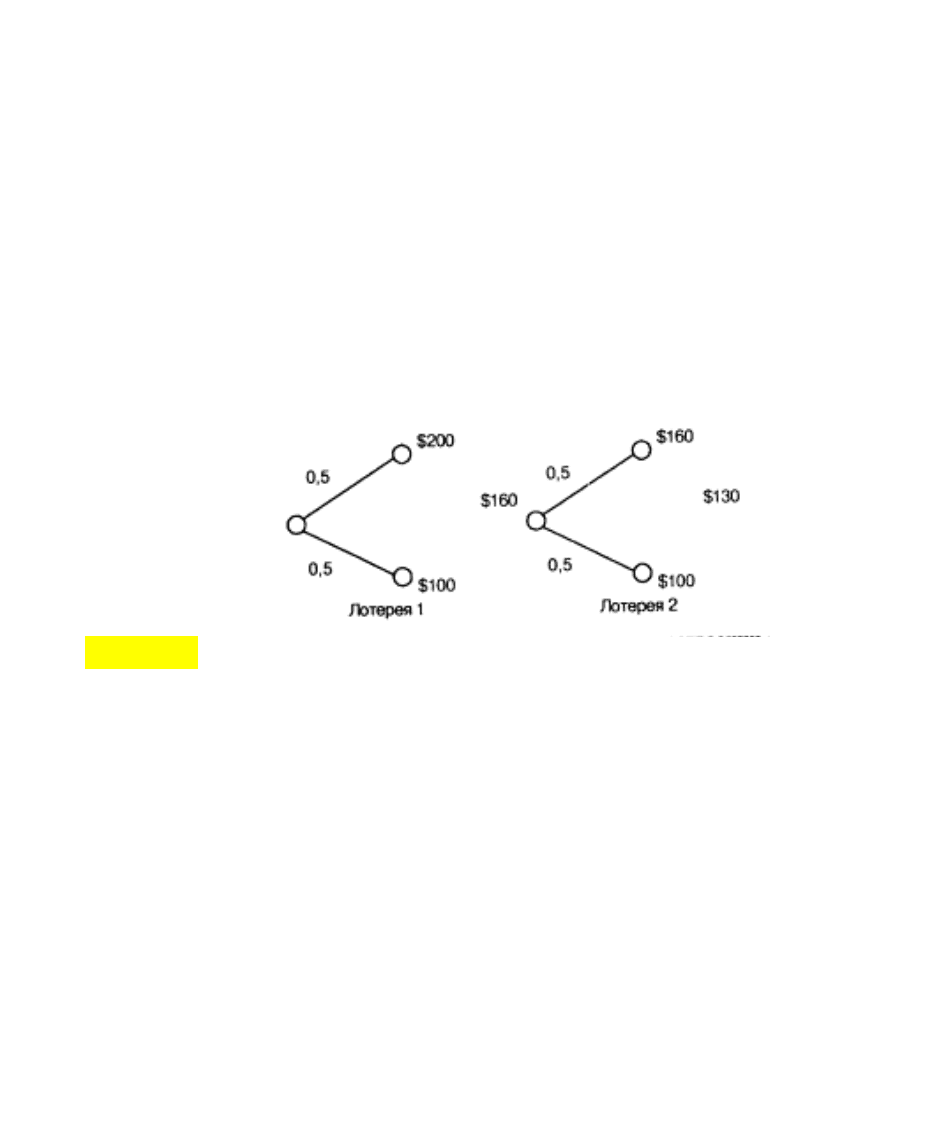
получаемым с вероятностью р, и исходом у, получаемым с вероятностью 1-р.

В лотерее 1 на рисунке 7 (слева) перед ЛПР ставится следующая задача:

«Определите эквивалент определенности для лотереи, имеющей с равными

вероятностями (р=0,5) минимальную и максимальную стоимости

постройки». ЛПР предъявляют ряд значений (например, $120 млн, $130

млн и т. д.) и спрашивают: выше или ниже данного значения находится, по

его мнению, эквивалент определенности. Предположим, что ЛПР

остановился на значении $160 млн. Тогда делается вывод, что U=0,5

соответствует $160 млн. Аналогично определяются другие значения функции

полезности. Так, правая лотерея на рисунке 8 позволяет определить точку

U($130 млн)=0,85. Идентичным образом строятся функции полезности для

каждого из критериев.

Рис. 4.10. Типовые лотереи, используемые при построении функции

полезности по одному критерию

Проверка условий независимости

Для определения общей функции полезности необходимо проверить

условия независимости по полезности и независимости по предпочтению.

Проверку условия независимости по полезности можно совместить с

предыдущим этапом построения однокритериальных функций полезности.

Сначала лицу, принимающему решение, сообщается, что при нахождении

эквивалента определенности он должен принять во внимание, что по

остальным критериям имеются наилучшие значения. Затем перед ЛПР

ставится та же задача, но уже при предположении, что по прочим

критериям имеются наихудшие значения. Если эквивалент

определенности в двух случаях одинаков, то делается вывод, что критерий

не зависит по полезности от прочих критериев.

Отметим, что для полноты проверки условия независимости по

полезности следует осуществлять эту проверку для всех лотерей. Однако

часто довольствуются приближенной проверкой — только для первой из

лотерей, используемых при построении однокритериальных функций

полезности.

При проверке условия независимости по предпочтению рассматривают

плоскости, где по осям отложены значения двух критериев. Сначала

предполагается, что по прочим критериям имеются наилучшие значения.

Первоначально ЛПР должен определить свое предпочтение между

альтернативами [(C

)min; (C

)max] и [(C

)max; (C

)min]. Рассматриваем две

крайние точки А и В. Обычно такая проверка считается достаточной.

Предположим, что вариант А предпочтительнее. Далее определяется

такая точка на шкале критерия С

, что варианты А и К одинаково

предпочтительны для ЛПР. Затем точно такой же поиск точки безразличия

осуществляется при другом значении С

. Если результаты совпадают, то

делается вывод, что пара С

, С

не зависит по предпочтению от третьего

критерия.

Для полной проверки условия независимости по предпочтениям следует

рассмотреть все пары критериев. Однако при приближенной проверке

выбираются один или два наиболее существенных критерия и прочие

рассматриваются только в паре с ними. Нарушение условий независимости

существенно усложняет задачу.

Определение весовых коэффициентов (коэффициентов важности)

критериев

В MAUT существенно используется понятие весов (коэффициентов

важности) критериев. Считается, что ЛПР может найти коэффициенты -

числа, которые определяют важность критериев. Отношения между весами

критериев устанавливаются поиском точек безразличия на плоскостях двух

критериев. В отличие от проверки условий независимости по предпочтению,

по осям упорядочиваются значения критериев от худших к лучшим.

Пусть альтернативы А и К находятся в отношении безразличия, которое

определяется так же, как и при проверке условия независимости по пред-

почтению. В точке равновесия полезности альтернатив равны. Используя

полученные ранее однокритериальные функции полезности, находим

соотношение весов этих двух критериев. Аналогичным образом определяется

соотношение между весами критериев С

и С

. Итак, мы выразим веса всех

критериев через вес наиболее важного из них и упорядочим критерии по

важности.

Для нахождения численного значения веса критерия C

(и,

следовательно, всех критериев) ЛПР предлагается сравнить две стратегии и

определить вероятность р, при которой обе стратегии равноценны.

Предположим, что такое р найдено. Тогда U(A)=U(B), или wi =р.

Определение полезности альтернатив

После нахождения весов критериев и построения однокритериальных

функций полезности задача решена. Действительно, найдена общая функция

полезности. В соответствии с теоретическими результатами остается

установить вид функции полезности. Например, сумма коэффициентов

важности критериев





1.1

. Считая полученное значение достаточно

близким к единице, выбираем аддитивную форму представления функции

полезности:

)()(

xUwxU





. (4.41)

Зная оценки альтернатив, можем подставить их в эту формулу,

определить полезность каждой альтернативы, сравнить полезности и выбрать

альтернативу с наибольшей полезностью.

Общая характеристика подхода MAUT

Подчеркнем положительные стороны подхода MAUT. Прежде всего,

построена единая стройная математическая теория, позволяющая обосновать

конкретный вид общей функции полезности в зависимости от предпочтений

ЛПР. Отметим также, что хотя построение общей функции полезности

требует достаточно много времени и усилий ЛПР, полученный результат

позволяет оценить любые (в том числе и вновь появляющиеся) альтернативы.

Два основных недостатка, связанные с подходом MAUT, стали

очевидными в настоящее время. Во-первых, предполагается (неявно), что

человек может делать точные количественные измерения. Это далеко не так.

Например, психологические исследования показали, что нет надежного

способа количественного измерения весов критериев. Во-вторых, подход

MAUT требует от ЛПР «немедленного» назначения всех основных

параметров, не давая ему возможности провести исследования проблемы

привычным для человека методом «проб и ошибок».

Подход аналитической иерархии

Подход аналитической иерархии (Analytic Hierarchy Process — АНР)

широко известен в настоящее время. Метод MAUT наиболее целесообразен

при решении задач второй группы. Действительно, построение функции

полезности осуществляется независимо от того, заданы или нет конкретные

альтернативы. Ясно, что одни и те же диапазоны значений критериев

возможны при различных альтернативах. Кроме того, диапазоны могут быть

заданы без указания реальных альтернатив, как это бывает во второй группе

задач принятия решений.

При подходе MAUT одни и те же усилия ЛПР по построению функции

полезности могут быть затрачены при большом и малом числе альтернатив.

Не всегда такой подход является обоснованным. В случае небольшого числа

заданных альтернатив (задачи первой группы) представляется разумным

направить усилия ЛПР на сравнение только заданных альтернатив. Именно

такая идея лежит в основе метода АНР.

Основные этапы подхода АНР

Постановка задачи, решаемой с помощью метода АНР, заключается

обычно в следующем.

Дано: общая цель (или цели) решения задачи; критерии оценки

альтернатив; альтернативы.

Требуется: выбрать наилучшую альтернативу. Подход АНР состоит из

совокупности этапов.

1. Первый этап заключается в структуризации задачи в виде

иерархической структуры с несколькими уровнями: цели – критерии –

альтернативы.

2. На втором этапе ЛПР выполняет попарные сравнения элементов

каждого уровня. Результаты сравнений переводятся в числа.

3. Вычисляются коэффициенты важности для элементов каждого

уровня. При этом проверяется согласованность суждений ЛПР.

4. Подсчитывается количественный индикатор качества каждой из

альтернатив и определяется наилучшая альтернатива.

Рассмотрим эти этапы подробнее применительно к основному методу

АНР, разработанному Т.Саати.

Для применения этого метода необходимо определить: цель, состав крите-

риев - C

,...,C

; перечень альтернатив А

, A

,..., A

. Предпо-

лагается, что все перечисленные альтернативы влияют на каждый из

приведенных критериев. Анализируемая проблема представляется в виде ие-

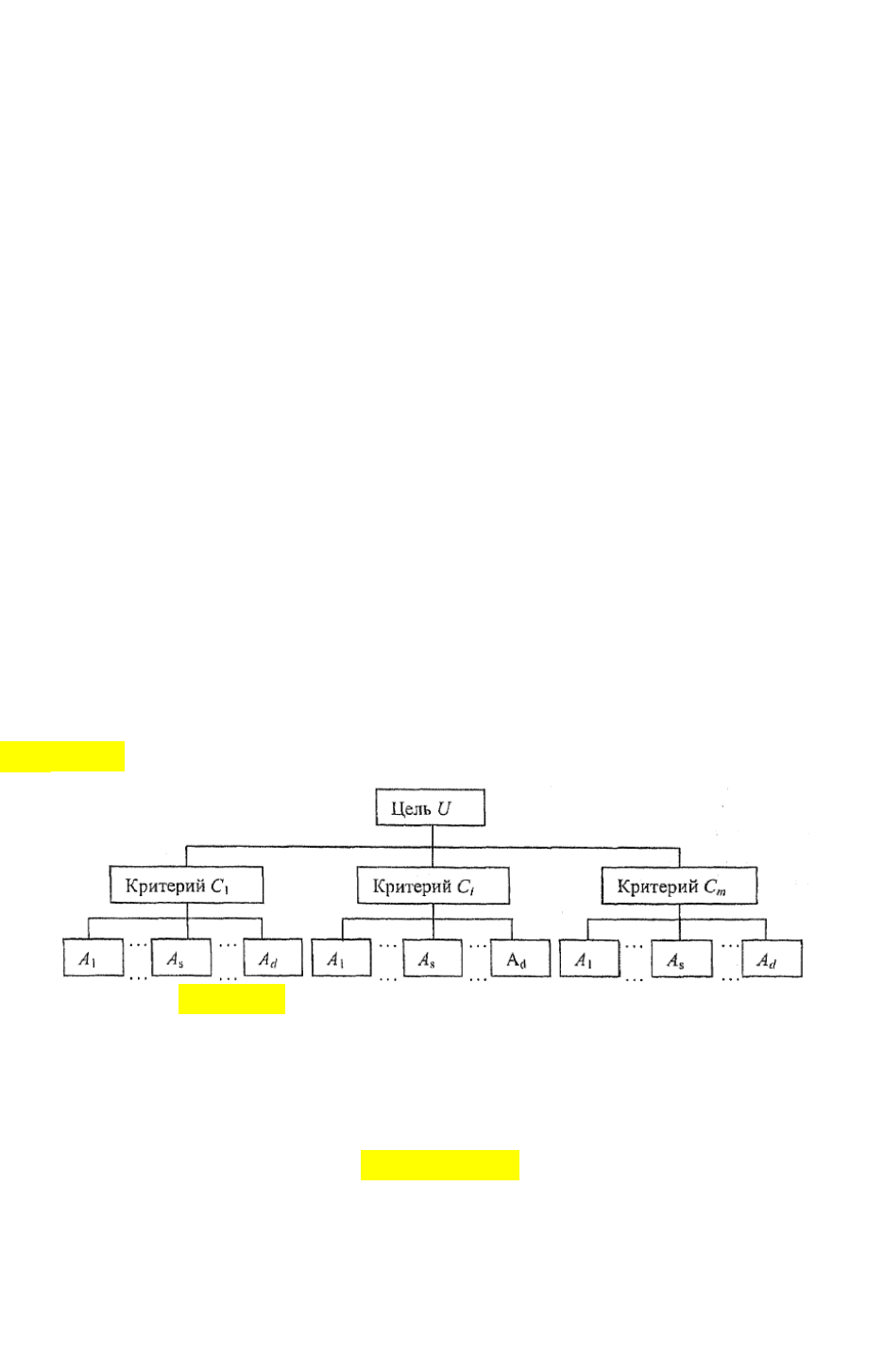
рархической структуры: на первом уровне размещается цель, на втором

уровне — состав критериев; на третьем уровне - множество альтернатив

(Рис. 4.11).

Рис. 4.11. Иерархическое представление проблемы

Попарные сравнения

При попарных сравнениях в распоряжение ЛПР дается шкала

словесных определений уровня важности, причем каждому определению

ставится в соответствие число (таблица 4.9).

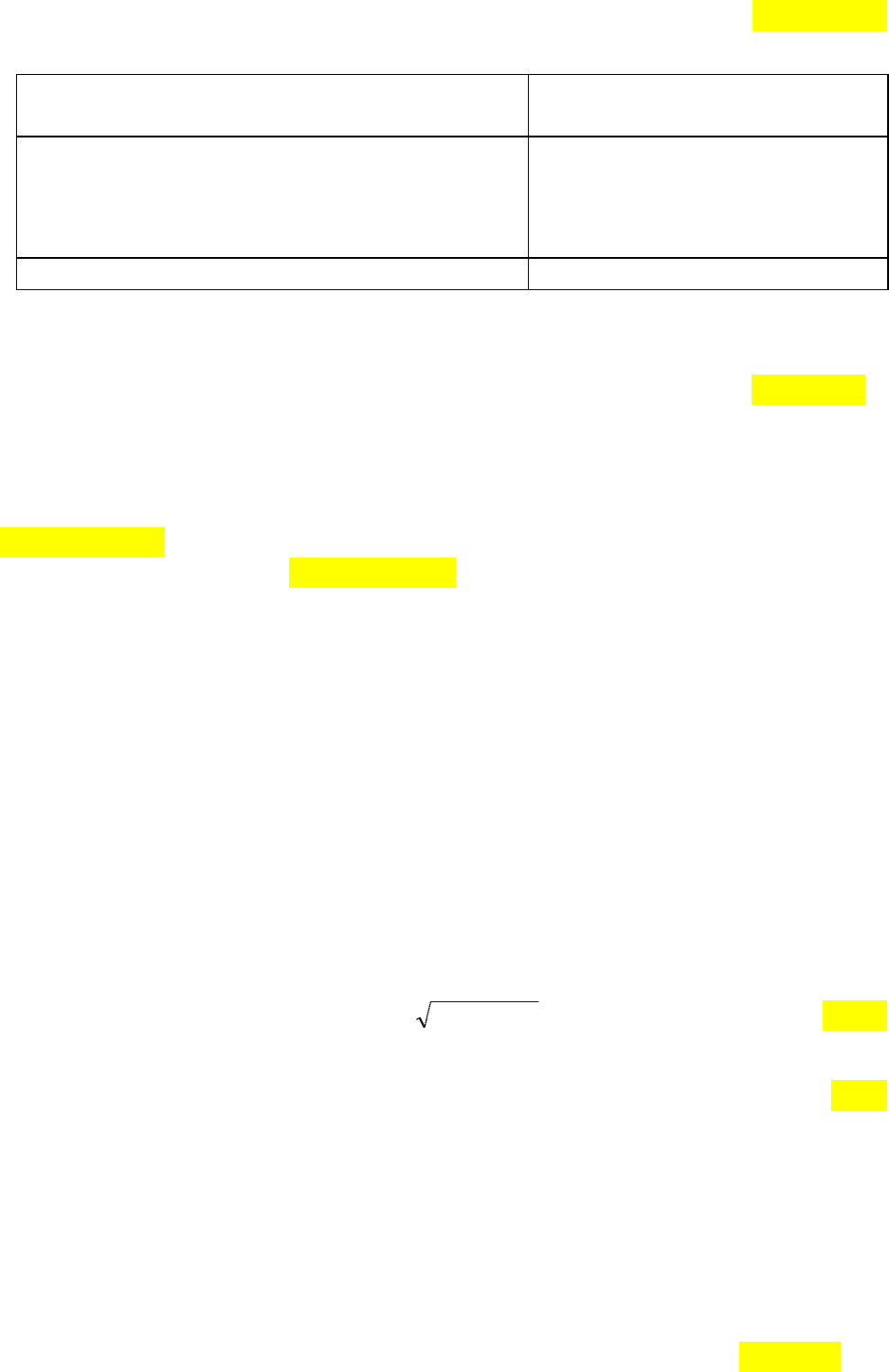
Таблица 4.9

Шкала относительной важности

Уровень важности Количественное

значение

Равная важность

Умеренное превосходство

Существенное или сильное превосходство 5

Значительное (большое) превосходство 7

Очень большое превосходство

При сравнении элементов, принадлежащих одному уровню иерархии,

ЛПР выражает свое мнение, используя одно из приведенных в таблице 4.9

определений. В матрицу сравнения заносится соответствующее число.

На нижнем уровне иерархической схемы сравниваются заданные

альтернативы (конкретные площадки) по каждому критерию отдельно.

Количественные результаты предпочтения альтернатив представлены в

таблице 4.10. Аналогичная таблица формируется для количественных

предпочтений критериев (таблица 4.11).

Вычисление коэффициентов важности

Матрица сравнений для критериев и относительная важность

альтернатив по отдельным критериям позволяют рассчитать коэффициенты

важности соответствующих элементов иерархического уровня. Для этого

нужно вычислить собственные векторы матрицы, а затем пронормировать их.

Определение элементов матрицы производится в соответствии со сле-

дующим правилом: если альтернатива A

превосходит альтернативу А

, то

элемент a

= {3,5,7,9}, а в случае равнозначности альтернатив А

и A

, a

=1.

Тогда элемент a

равен обратному значению а

т.е. а

= l/a

. Диагональные

элементы a

равны единице. Для вычисления 

элемента собственного

вектора матрицы необходимо определить произведение элементов s-й

строки, а затем найти корень d-й степени, т.е.

sdsss

aaa ...





. (4.42)

Вес v

- это нормированное значение 

, т.е.

.1;/





sss



(4.43)

Таким же способом на основе относительной важности альтернатив по

отдельным критериям можно рассчитать важность каждой из площадок по

каждому из критериев.

Таблица 4.10

Количественные предпочтения альтернатив

Альтернативы

Собственны

й вектор

Вес

… A

… a



… a



… … … … … … … … …

… a



… … … … … … … … …

… a



Таблица 4.11

Количественные предпочтения критериев

Критерий

Собственны

й вектор

Вес

… С

… C



… C



… … … … … … … … …

… C



… … … … … … … … …

… C



В книге Т. Саати (автора метода АНР) дается способ проверки

согласованности суждений ЛПР при заполнении каждой из матриц - путем

сравнения со случайно заполненной матрицей. Ясно, что при сравнительно

небольших ошибках ЛПР условие согласованности выполняется.

Определение наилучшей альтернативы

Синтез полученных коэффициентов важности осуществляется по

формуле

vwS





. (4.44)

где S

- показатель качества j-й альтернативы; w

– вес 1-го критерия; v

–

важность j-й альтернативы по i-му критерию.

В качестве оптимальной выбирается альтернатива А

, для которой

SS max

. (4.45)

Общая характеристика подхода АНР

Достоинством метода АНР, привлекающим внимание многих

пользователей, является направленность на сравнение реальных альтернатив.

Отметим, что метод АНР может применяться и в тех случаях, когда

эксперты (или ЛПР) не могут дать абсолютные оценки альтернатив по

критериям, а пользуются более слабыми сравнительными измерениями.

Метод АНР позволяет решить ряд практических задач.

Недостатки метода АНР неоднократно обсуждались в статьях различных

авторов. Среди них наиболее существенными являются два. Прежде всего

введение новой, недоминирующей альтернативы может в общем случае

привести к изменению предпочтений между двумя ранее заданными

альтернативами (rank reversals). Весьма существенной проблемой является,

на наш взгляд, необоснованный переход к числам при проведении

измерений, оторванность метода объединения оценок от предпочтений ЛПР.

Дальнейшее развитие подход АНР получил в виде методов

мультипликативной аналитической иерархии и метода MACBETH.

Методы ELECTRE ранжирования многокритериальных альтернатив

В конце 60-х годов группа французских ученых во главе с проф. Б. Руа

предложила подход к попарному сравнению многокритериальных

альтернатив, не основанный на теории полезности. В отличие от MAUT

оценка каждой альтернативы является не абсолютной, а относительной (по

сравнению с другой альтернативой). Так возник метод ELECTRE

(ELimination Et Choix Traduisant la Realite - исключение и выбор,

отражающие реальность). В настоящее время разработан ряд методов семей-

ства ELECTRE.

Методы ELECTRE направлены на решение задач с уже заданными

многокритериальными альтернативами. Следовательно, они принадлежат к

методам первой группы согласно приведенной выше классификации. В

отличие от метода АНР в методах ELECTRE не определяется количественно

показатель качества каждой из альтернатив, а устанавливается лишь условие

превосходства одной альтернативы над другой.

Постановка задачи обычно имеет следующий вид:

Дано: N критериев со шкалами оценок (обычно количественные), веса

критериев (обычно целые числа), альтернативы с оценками по критериям.

Требуется: выделить группу лучших альтернатив.

Основные этапы методов ELECTRE

1. На основании заданных оценок двух альтернатив подсчитываются

значения двух индексов: согласия и несогласия. Эти индексы определяют

согласие и несогласие с гипотезой, что альтернатива А превосходит

альтернативу В.

2. Задаются уровни согласия и несогласия, с которыми сравниваются

подсчитанные индексы для каждой пары альтернатив. Если индекс согласия

выше заданного уровня, а индекс несогласия - ниже, то одна из альтернатив

превосходит другую. В противном случае альтернативы несравнимы.

3. Из множества альтернатив удаляются доминируемые. Оставшиеся

образуют первое ядро. Альтернативы, входящие в ядро, могут быть либо

эквивалентными либо несравнимыми.

4. Вводятся более «слабые» значения уровней согласия и несогласия

(меньший по значению уровень согласия и больший уровень несогласия),

при которых выделяются ядра с меньшим количеством альтернатив.

5. В последнее ядро входят наилучшие альтернативы. По-

следовательность ядер определяет упорядоченность альтернатив по качеству.

Рассмотрим эти этапы подробнее, используя в качестве иллюстрации все

тот же пример выбора площадки для постройки аэропорта.

Индексы согласия и несогласия

В различных методах семейства ELECTRE индексы согласия и

несогласия строятся по-разному. Основные идеи построения этих индексов

далее будут показаны на примере метода ELECTRE 1.

Каждому из N критериев ставится в соответствие целое положительное

число р, характеризующее важность критерия. Б. Руа предложил

рассматривать р как «число голосов» членов жюри, голосующих за важность

данного критерия.

Выдвигается гипотеза о превосходстве альтернативы А над

альтернативой В. Множество I, состоящее из N критериев, разбивается на три

подмножества:

– подмножество критериев, по которым А

предпочтительнее А

;

– подмножество критериев, по которым А

равноценно А

;

– подмножество критериев, по которым А

предпочтительнее А

Далее формулируется индекс согласия с гипотезой о превосходстве А

над А

. (В других методах семейства ELECTRE используются индексы

сильного и слабого превосходства.)

Формитуется таблица индексов согласия, строки и столбцы которой

соответствуют множеству альтернатив. Индекс согласия определяет степень

согласия перспективности альтернативы А

по отношению к альтернативе А

Индекс согласия подсчитывается на основе весов критериев. Так, в

методе ELECTRE1 этот индекс определяется как отношение суммы весов

критериев подмножеств I

и I

к общей сумме весов:











IIi

iAA

wwc

. (4.46)

Таблица индексов согласия имеет следующий вид (таблица 4.12).

Далее конструируется таблица индексов несогласия, строки и столбцы

которой соответствуют множеству альтернатив. Индекс несогласия u

AsAr

определяет степень отрицания гипотезы о перспективности альтернативы А

по отношению к альтернативе А

. Индекс несогласия с гипотезой о

превосходстве А

над А

определяется на основе самого «противоречивого»

критерия — критерия, по которому А

в наибольшей степени превосходит А

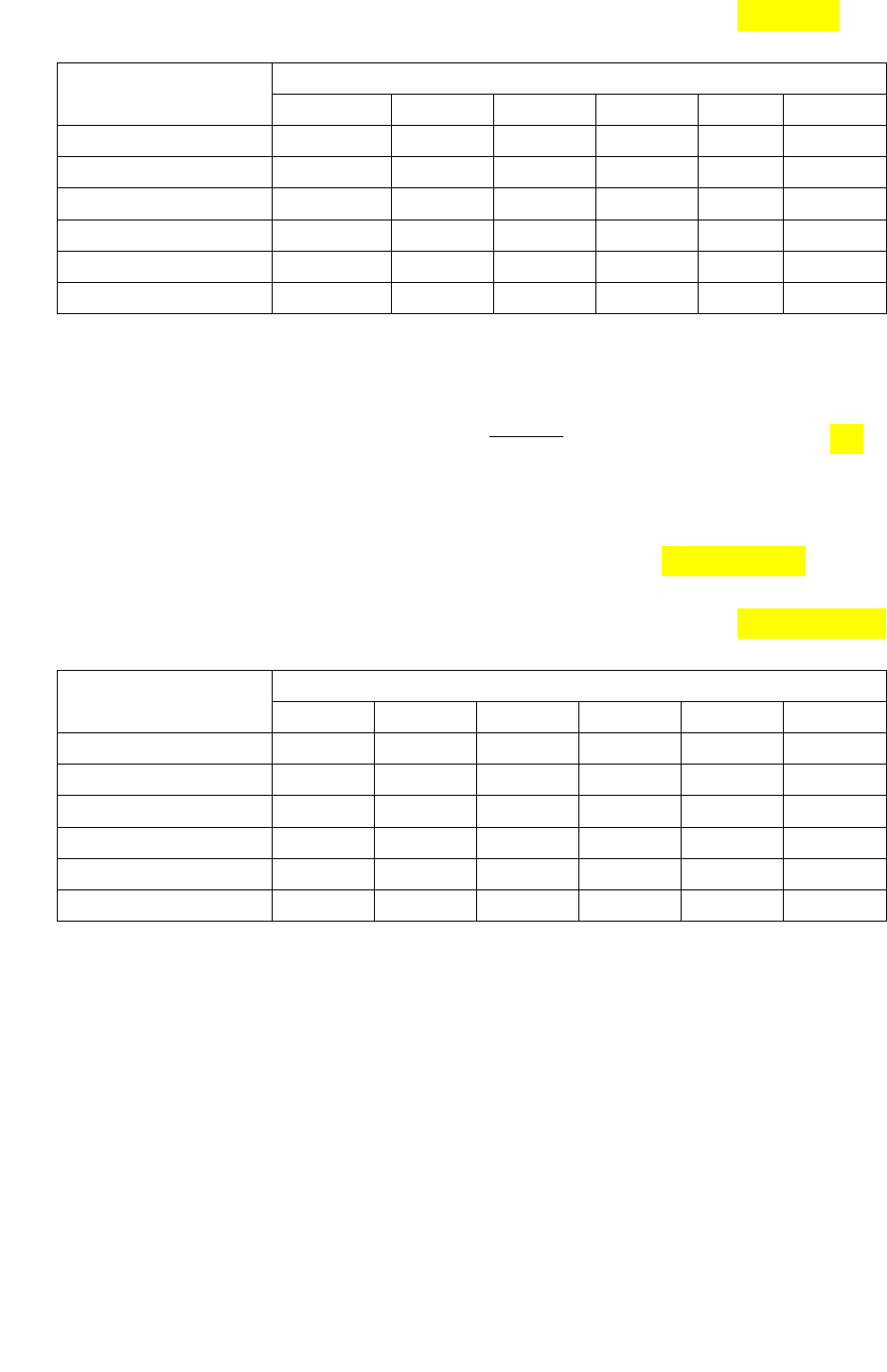
Таблица 4.12

Индексы согласия

Альтернативы

… A

* с

… с

* … с

… с

… … … … … … …

… с

… … … … … … …

… с

… *

Чтобы учесть возможную разницу длин шкал критериев, разность

оценок относят к длине наибольшей шкалы:

isir









max

. (4.47)

где

– оценки альтернатив А

и А

по i-му критерию; L

– длина

шкалы i-го критерия.

Таблица индексов несогласия имеет следующий вид (таблица 4.13).

Таблица 4.13

Индексы несогласия

Альтернативы

… A

* u

… u

* … u

… u

… … … … … … …

… u

… … … … … … …

… u

… *

Укажем очевидные свойства индекса согласия:

1)0 < С

АВ

< 1;

2) c=1> если подмножество I

- пусто;

2) c

сохраняет значение при замене одного критерия на несколько

с тем же общим весом.

Приведем свойства индекса несогласия:

1) 0<u

< 1;

2) u

сохраняет значение при введении более детальной шкалы по

i-му критерию при той же ее длине.

Бинарные отношения. Выделение ядер

В методе ELECTRE 1 бинарное отношение превосходства задается

уровнями согласия и несогласия. Если c

≥ с

и u

≤u

, где с

, u

– заданные

уровни согласия и несогласия, то альтернатива А объявляется лучшей по