Кармелюк Г.І. Теорія ймовірностей та математична статистика
Подождите немного. Документ загружается.


101
×
⋅
+
⋅
−
⋅
−
⋅
−⋅−
2143423241
()()()()( AAPAAPAAPAAPAAP
−
⋅
⋅
+
⋅
⋅
+
⋅⋅+× )()()()
4314324213
AAAPAAAPAAAPA
−
+
+
+
=
⋅⋅⋅− )()()()()(
43214321
APAPAPAPAAAAP
×
−
⋅
−
⋅
−⋅− )()()()()()()(
2413121
APAPAPAPAPAPAP
×
⋅
+
⋅
−
⋅−× )()()()()()()(
2143423
APAPAPAPAPAPAP
+
⋅
⋅
+
⋅
⋅+× )()()()()()()(
4324213
APAPAPAPAPAPAP
=
⋅
⋅
⋅
−
⋅⋅+ )()()()()()()(
4321431
APAPAPAPAPAPAP
−
⋅
−
⋅
−
⋅
−
+++= 9,07,08,07,075,07,09,08,075,07,0
×
⋅
+
⋅
⋅
+
⋅
−
⋅−⋅− 75,07,08,075,07,09,08,09,075,08,075,0
=
⋅
⋅
⋅
−
⋅
⋅
+
⋅⋅+× 9,08,075,07,09,08,07,09,08,075,09,0
+
+
−
−
−
−
−−= 42,072,0675,06,063,056,0525,015,3
9985,0378,0504,054,04725,0
=
−
+++ .
2.1.36. Довести, що
)(
)(
1)(
AP
BP
BP
A
−≥ .
Розв’язок.
Оскільки події
В і
B
протилежні (утворюють повну гру-
пу подій), то
1)()( =+ BPBP , і 1)()( =+ BPBP
AA
. Отже,
)(1)( BPBP
AA
−= ; але ×=⋅=⋅ )()()()( BPBPAPBAP
A
)(AP
B
× , звідки .
)(
)()(
)(
AP
APBP
BP
B
A
⋅
=
Отже,
)(
)()(
1)(
AP
APBP
BP
B
A
⋅
−=
.
Але
)()()( APBPBP
B
⋅≥ , оскільки 1)(
≤
AP
B
. Замі-
нивши в останньому рівнянні чисельник на більше значення
Р(
В
), отримаємо нерівність:
)(
)(
1)(
AP
BP
BP
А
−≥ .
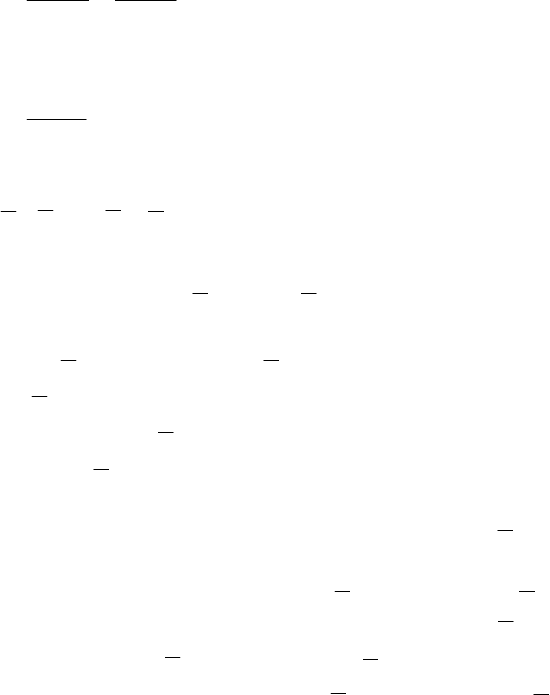
102
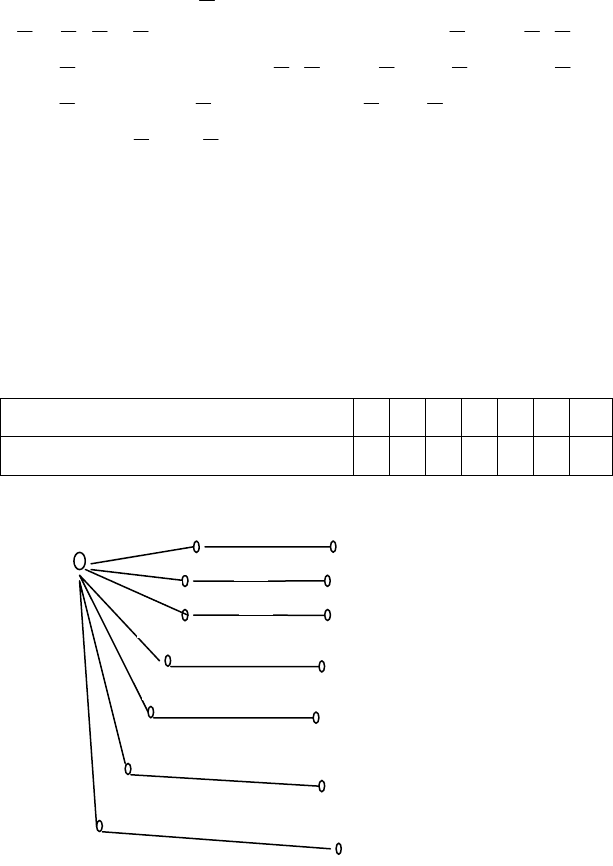
2.1.37. Нехай відомо, що Р
В
(А) > Р(А). Довести тоді, що
Р
А
(В) > Р(В).
Розв’язок.
Використаємо формулу імовірності добутку двох
залежних подій:
Р(АВ) = Р(А)Р
А
(В) = Р(В)Р
В
(А), звідки
)(
)(
)(
)(
BP
BP
AP
AP
AB
= .
За умовою
Р
А
(В) < Р(В), отже, дріб зліва менший 1, тому
й дріб справа менший 1:
.1
)(
)(
<
BP
BP
A
Звідси Р(В) < Р
А
(В), або Р
А
(В) > Р(В).
2.1.38. Довести, що якщо події А і В незалежні, то події А
і
B
, A і B, A і
B
також незалежні.
Розв’язок.
Подію
А можна подати як суму двох подій, що перети-
наються
B
A
⋅
і
B
A
⋅
:
B
A
B
AA
⋅
+
⋅
=
. Оскільки події А і
В незалежні, то )()()( BPAPBAP
⋅
=
⋅
. Тоді =)(AP
)()()()()( BPAPBAPBAPBAP ⋅+⋅=⋅+⋅= . Але +)(BP
1)( =+ BP , як сума імовірностей протилежних подій.
Звідси,
[
]
=−=⋅−=⋅ )(1)()()()()( BPAPBPAPAPBAP
)()( BPAP ⋅= .
Але імовірність добутку двох подій дорівнює добутку їх
імовірностей, якщо ці події незалежні. Отже,
BA i – не-
залежні події. Аналогічно подамо подію
В, як суму двох
подій, що перетинаються
AB і
B
A
⋅
:
B
A
B
A
B
⋅
+
⋅
=
.
Імовірність події
В рівна: =⋅+⋅= )()()( BAPBAPBP
)()()( BAPBPAP ⋅+⋅= , звідки
×−=⋅ )()()( APBPBAP
).()())(1)(()( APBPAPBPBP ⋅=−=× Отже, події А і
B
–
незалежні.
103
Подамо подію A як суму двох подій, що перетинаються:
B
A
B
AA ⋅+⋅= . Імовірність події +⋅= )()( BAPAP
)( BAP ⋅+ , звідси −=⋅−=⋅ )()()()( APBAPAPBAP
)()()](1)[()()( BPAPBPAPBPAP ⋅=−=⋅− , як доведено
вище, отже,
BA i також незалежні.
2.1.39. Кинуто два гральних кубики. Всі комбінації рівно-
ймовірні.
Знайти умовну ймовірність того, що випали дві п'ятірки,
якщо відомо, що сума очок, що випали, ділиться на п'ять.
Розв’язок.
Сума очок, що випали, ділиться на п’ять, якщо відбу-
дуться такі наслідки випробувань:
Кількість очок на І кубику 1 4 2 3 4 6 5
Кількість очок на ІІ кубику 4 1 3 2 6 4 5
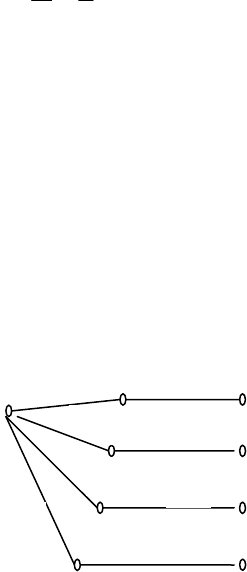
Рис. 2.1.6.
4
1
1
4
3
2
3
2
4
6
6
4
5
5
(1,4)
(4,1)
(2,3)
(3,2)
(4,6)
(6,4)
(5,5)
А
1
А
2
А
3
А
4
А
5
А
6
А
7
104
Це можна зобразити графічно на дереві імовірностей
(рис. 2.1.6):
Нехай подія
А означає, що сума очок ділиться на 5. Вона
може відбутися при настанні однієї з несумісних подій:
А
1
,...А
7
.
Подія
В – означає, що випали дві п’ятірки. Це відповідає
лише одній події
А
7
. Тоді умовна імовірність події В
.
7
1
)( ==
n
m
BP
A
2.1.40. З множини всіх родин, які мають двох дітей,
обрано одну родину. Всі елементарні події однаково ймовірні.
Яка ймовірність того, що:
а) в цій родині два хлопчики, якщо відомо, що в ній є
один хлопчик?
б) в родині два хлопчики, якщо відомо, що старша дитина
– хлопчик?
Розв’язок.
Простір елементарних подій
має вигляд:
{}
XXXDDXDD ,,,=Ω . Зобразимо їх на дереві імовір-
ностей (рис. 2.1.7):
Рис. 2.1.7.
Д
Д
Д Х
Х
Д
Х
Х

105
Нехай
{}
XXA = – подія, яка полягає в тому, що в родині
є два хлопчики,
{
}
XXXDDXB ,,
=
– подія, яка полягає в
тому, що в родині є хоч би один хлопчик;
{
}
XXXDC ,
=
–
подія, яка полягає в тому, що старша дитина – хлопчик.
Тоді:
а) Через залежні події дана імовірність шукається так:
3
1
4/3
4/1
)(
)(
)( ==
⋅
=
BP
BAP
AP
B
; або
3
1
)( =AP
B
– лише
один наслідок
{}
XX випробувань з усіх трьох можливих
{}
XXXDDX ,, відповідає даній події.
б)
2
1
4/2
4/1
)(
)(
)( ==
⋅
=
CP
CAP
AP
C
; або
2
1
)( =AP
C
– лише
один наслідок
{}
XX
– випробувань з двох можливих
{}
XXXD, відповідає даній події.
2.1.41.
З 100 карточок з числами 00, 01,...., 98, 99
випадково вибирається одна. Нехай
1
η
і
2
η
відповідно сума і
добуток цифр на вибраній карточці. Знайти
}
{
0|
21
=
=
η
η
iP ,
і = 0, 1, ..., 18.
Розв’язок.
Нехай подія
}
{
0
2
=
=
η
A означає, що добуток цифр на
вибраній карточці рівний 0. Даній події відповідає такий набір
з 19 чисел: {00; 01; 02; 03; 04; 05; 06; 07; 08; 09; 10; 20; 30; 40;
50; 60; 70; 80; 90}.Подія
}
{
iB
i
=
=
1
η
означає, що сума цифр
вибраного числа рівна
і. Тоді події
}
{
0|0
21
=
=
=
η
η
i
C –
яка означає, що сума цифр вибраного числа рівна нулю за
умови, що їх добуток рівний нулю, відповідає одне число
“00”. Тому імовірність події С
0
рівна,
19
1
)()(
00
== BPCP
A
.

106
Події
}{
0|1
21
=
=
=
η
η
i
C відповідають два числа: “01” і
“10”. Отже
19
2
)()(
11
== BPCP
A
. Аналогічно,
}
{
0|
21
=
=
=
η
η
iC
i
і
9
2
)()( ==
iAi
BPCP для і = 1, 2,... 9. Оскільки, нема жодного
з перерахованих вище чисел, у яких би сума була більшою 10
(
10
1
≥
η
), то 0)()(
=
=
iAi
BPCP , для і=10, 11, ...18.
2.1.42. Серед усіх родин з двома дітьми обрано одну.
Описати простір елементарних подій і випадкові події:
А
“в родині є хлопчик і дівчинка”,
В – “в родині не більше
однієї дівчинки”. Всі елементарні події однаково ймовірні.
Обчислити
Р(А), Р(В), Р(АВ) і довести, що події А і В
залежні.
Розв’язок.
Простір елементарних подій
{
}
XXXDDXDD ,,,
=
Ω
.
Нехай
{}
XDDXA ,= – подія, яка полягає в тому, що в
родині є дівчинка і хлопчик,
{
}
XXXDDXB ,,
=
– подія, яка
полягає в тому, що в родині не більше однієї дівчинки
(включає подію
ХХ – в родині немає жодної дівчинки). Тоді
4
3
)(,
2
1
4
2
)( === BPAP
, добуток подій
{
}
XDDXBA ,
=
⋅
.
Тому
2
1
4
2
)( ==AP
.
Для визначення того, чи події
А і В є залежними, пере-
віримо виконання рівності:
)()()( BPAPBAP
⋅
=
⋅
. Якщо рів-
ність справджується, то події є незалежними, якщо не справ-
джується, то події є залежними.

107
Але
2
1
)( =⋅ BAP
і
8
3
4
3
2
1
)()( =⋅=⋅ BPAP
. Отже,
8
3
2
1
≠
або )()()( BPAPBAP
⋅
≠
⋅ , тому події А і В є залеж-
ними.
ІІ спосіб.
Визначимо умовні імовірності подій:
3
2
4/3
4/2
)(
)(
)( ==
⋅
=
BP
BAP
AP
B
; отже,
)(
3
1
2
1
)( APAP
B
=≠= .
Отже, події
А і В – залежні.
1
4/2
4/2
)(
)(
)( ==
⋅
=
AP
BAP
BP
A
; )(1
4
3
)( BPBP
A
=≠= .
Отже, події
А і В – залежні.
ІІІ спосіб.
Позначимо події:
А
1
– першою народилася дівчинка; А
2
–
другою народилася дівчинка;
В
1
– першим народився хлоп-
чик;
В
2
– хлопчик народився другим.
Простір елементарних подій:
21212121
ABBABBAA
+
+
+
.
Подія
21212121
ABBAABBAA ∪
=
+
= і, оскільки
2
1
)()()()(
2121
==== BPBPAPAP , то
2
1
2
1
2
1
2
1
2
1
)( =⋅+⋅=AP
.
Подія
212121
ABBABBB ∪∪=
. Отже,
4
3
2
1
4
1
)( =+=BP
;
тому
8
3
4
1
2
1
)()( =⋅=⋅ BPAP
. Але
)/()()( ABPAPBAP
=
×
,
де
)()()/( BPBPABP
A
=
= , якщо А і В незалежні і
1)()/( == BPABP
A
у даному випадку.
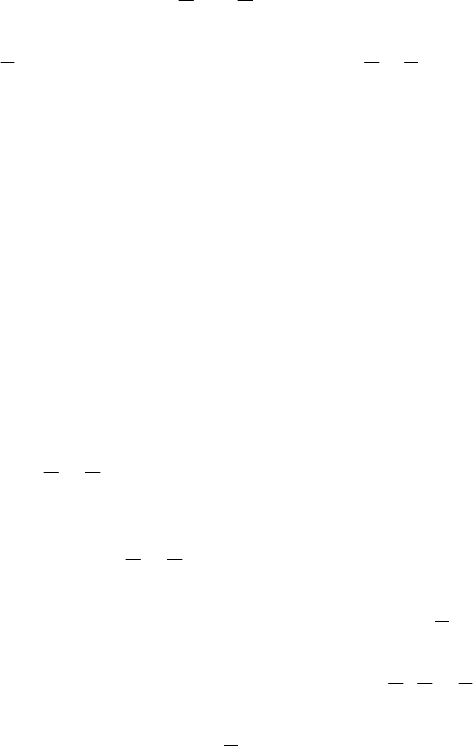
108
Тому
2
1
1
2
1
)( =⋅=× BAP
і )()/( BPABP
А
≠
, оскільки
8
3
1 ≠
і )()()( BPAPBAP
⋅
≠× , оскільки
8
3
2
1
≠
.
Отже, події
А і В залежні.
2.1.43. Серед усіх родин з трьома дітьми обрали одну.
Описати простір елементарних подій і випадкові події:
А
“в родині є хлопчик і дівчинка”,
В – “в родині не більше од-
нієї дівчинки”. Всі елементарні події однаково ймовірні.
Обчислити
P(A), P(B), P(A B) і довести, що події А і В
незалежні.
Розв’язок.
Простір елементарних подій такий:
{}
DXXXDXXXDDDDDDXDXDXDDXXX ,,,,,,,=Ω .
Нехай
{}
DDXDXDXDDDXXXDXXXDA ,,,,,= – по-
дія, яка полягає в тому, що в родині є хлопчик і дівчинка, тоді
4
3
8
6
)( ==AP
. Нехай
{
}
DXXXDXXXDXXXB ,,,
=
– подія,
яка полягає в тому, що в родині не більше однієї дівчинки,
звідки
2
1
8
4
)( ==BP
. Добуток подій А і В такий:
{}
XXDDXXXDXBA ,,=× , звідки,
8
3
)( =× BAP
. Обчисли-
мо добуток імовірностей
8
3
2
1
4
3
)()( =⋅=× BPAP
. Отже,
8
3
)()()( =×=× BPAPBAP
, а така рівність можлива, коли
події
А і В незалежні.
2.1.44. Кинуті послідовно три монети. Розглядаються
події:
А={ випадання “тризуба” на першій монеті};

109
В={ випадання хоча б одного “тризуба”};
С={ випадання хоча б одного номіналу};
D={ випадання номіналу на другій монеті};
Е={ випадання “тризуба” на другій монеті};
Визначити залежні чи незалежні пари подій:
1)
А і С; 2) А і D; 3) В і D; 4) В і С; 5) В і Е; 6) А і Е; 7) С і
D.
Розв’язок.
Імовірність випадання „тризуба” рівна
2
1
=p
, “номіна-
лу”
2
1
=q
. Отже,
2
1
)()()( === EPDPAP
. Тоді імовір-
ність випадання хоча б одного “тризуба”
−=1)(BP
8
7
8
1
1
2
1
1)1)(1)(1(
3
=−=−=−−−− ppp
. Аналогічно, імо-
вірність випадання хоча б одного “номіналу” рівна:
8
7
2
1
1)1(1)1)(1)(1(1)(
3
3
=−=−−=−−−−= qqqqCP .
Тоді: 1)
4
3
2
1
2
1
1)1)(1(1)( =⋅−=−−−= qqCP
A
або
)()()( CPAPACP
A
⋅=
, звідки
4
3
84
83
)(
)(
)( ===
AP
ACP
CP
A
,
отже,
)()( CPCP
A
≠
і події А і С – залежні.
2)
;
2
1
)(;
2
1
)(;
2
1
)(;
2
1
)( ==== DPAPAPDP
AD
отже,
)()();()( DPDPAPAP
AD
=
=
, а тому події А і D – незалежні.
3) Зобразимо простір усіх елементарних подій:
,,,,,,(
321321321321321321
THHTTHTHTHTTHHHTTT=Ω
).,
321321
HHTHTH
Тоді простір подій
В – випадання хоча б одного “тризуба”
зобразиться так:
,,,,,(
3213213213213211
THHTTHTHTHTTTTT
=
Ω

110
),,
321321
HHTHTH отже,
8
7
)( =BP
, серед яких настанню
події
D – “випадання номіналу на другій монеті” буде
відповідати простір подій
),,(
3213213212
HHTTHHTHT
=
Ω
.
Таким чином,
7
3
)( =DP
B
, отже,
)()( DPDP
B
≠
. Але
4
3
2
1
1)1(1)1)(1(1)(
2
2
=−=−−=−−−= qppBP
D
або
=)(DBP
)()( BPDP
D
⋅=
, звідки
4
3
84
83
)(
)(
)( ===
DP
DBP
BP
D
. Отже,
)()( BPBP
D
≠
; тому події В і D залежні.
4) Для обчислення ймовірності
)(BP
C
зобразимо простір
Ω
3
подій С – “випадання хоча б одного номіналу”:
,,,,,,(
3213213213213213213
HTHTHHTTHTHTHTTHHH=Ω
)
321
HHT
, отже,
8
7
)( =CP
, серед яких настанню події В –
“випадання хоча б одного тризуба” буде відповідати простір
подій:
),,,,,(
3213213213213213214
HHTHTHTHHTTHTHTHTT=Ω
.
Отже,
7
6
)( =BP
C
, звідки, )()( BPBP
C
≠
, а, отже, події В
і
С залежні.
5)
1)( =BP
E
, отже, )()( BPBP
E
≠
;
7
4
)( =EP
B
,
)()( EPEP
B
≠ , тому – події В і Е залежні.
6)
;
2
1
)( =AP ,
2
1
)( =EP
;
2
1
)(;
2
1
)( == EPAP
AE
, отже,
)()();()( EPEPAPAP
AE
=
= , тому події А і Е незалежні.
7)
2
1
)(;
7
4
)( == DPDP
C
,тому )()( DPDP
C
≠
;
