Карасева А.Г. Неопределенный интеграл
Подождите немного. Документ загружается.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Методические указания
к выполнению типового расчета
по курсу «Математика»
Составитель А. Г. Карасева
Ульяновск
2009

2
УДК 519.85(075)
ББК 22.18я7
М 54
Рецензент: доктор техн. наук, профессор П. М. Попов.
Методические указания к выполнению типового расчета по К21
дисциплине «Математика» / сост. А. Г. Карасева. – Ульяновск :
УлГТУ, 2009. – 61 с.
Методические указания написаны в соответствии с УМК курса «Математика»
для студентов специальностей «Самолето-и вертолетостроение», «Информационные
системы и технологии». Рассмотрены различные методы интегрирования. Составлены
задачи для самостоятельного решения.
УДК 519.85(075)
ББК 22.18я7
Учебное издание
Уровень жизни и проблемы социальной ориентации
российской экономики
Составитель КАРАСЕВА Анна Георгиевна
Редактор Штаева М.
ЛР №020640 от 22.10.97.
Ульяновский государственный технический университет
432027, г. Ульяновск, ул. Сев. Венец, 32.
Типография УлГТУ, 432027, г. Ульяновск, ул. Сев. Венец, 32.
© А. Г. Карасева, составление, 2009
© Оформление, УлГТУ, 2009
М 54
3
ОГЛАВЛЕНИЕ
ОГЛАВЛЕНИЕ...................................................................................................................................3
ВВЕДЕНИЕ ........................................................................................................................................5
1. ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА ..........................................6
2. ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ...................................................................................7
3. ТАБЛИЧНОЕ ИНТЕГРИРОВАНИЕ............................................................................................9
4. ЗАМЕНА ПЕРЕМЕННОЙ: ВНЕСЕНИЕ ПОД ЗНАК ДИФФЕРЕНЦИАЛА.........................10
5. ЗАМЕНА ПЕРЕМЕННОЙ: ПОДСТАНОВКА..........................................................................11
6. ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ ..........................................................................................12
7. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ...........................................................14
7.1. Интегрирование простейших дробей. .................................................15
7.2. Интегрирование правильных дробей. .................................................17
7.3. Интегрирование неправильных дробей. .............................................19
8. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ............................................21
8.1. Интегралы вида
dxxxR
)cos,(sin
∫
. ....................................................21
8.2. Интеграл вида
∫
⋅ xdxx
nm
cossin
. ..........................................................23
8.3. Интегралы вида
∫∫
xdxctgxdxtg
mm
,
. ......................................................25
8.4.Интегралы вида
∫∫
⋅⋅ xdxecxctgxdxxtg
nmnm
cos ,sec
. ...........................25
8.5. Интегралы вида
∫
xdx
m2
sec
и
∫
xdxec
m2
cos
. .......................................26
8.6. Интегралы вида
∫∫
++
xdxecxdx
mm
1212
cos,sec
. ........................................26
8.7. Интегралы вида
∫∫∫
⋅⋅⋅ nxdxmxnxdxmxnxdxmx
sinsin ,coscos ,cossin
.27
9. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ................................................27
9.1. Интегралы вида
dx
dcx
bax
dcx
bax
dcx
bax
xR
k
k
q
p
q
p
q
p
),...,,,(
2
2
1
1
+
+
+
+
+
+
∫
. .....28
9.2. Интеграл вида dx
cbxax
BAx
∫
++
+
2
............................................................29
9.3. Интеграл вида
∫
++
dx
cbxax
xP
n
2
)(
. ..........................................................29
9.4. Интегралы вида
dxcbxaxxQ
m
++⋅
∫
2
)( . .........................................30
9.5. Интеграл вида
∫
++⋅−
dx
cbxaxmx
xP
n
2
)(
)(
. ...........................................31

4
9.6. Интеграл от дифференциального бинома...........................................32
9.7. Интеграл вида
∫
++ dxcbxaxxR ),(
2
. ...................................................34
10. ИНТЕГРИРОВАНИЕ ТРАНСЦЕНДЕНТНЫХ ФУНКЦИЙ ................................................ 37
10.1. Интеграл вида
∫
dxeR
ax
)(
. ...................................................................37
10.2. Интегралы вида
∫
⋅
)(
dxexP
ax
n
........................................................37
10.3. Интегралы вида
∫
⋅+⋅
dx xxQxxPe
mn
x
)sin)(cos)((
ββ
α
..................38
11. ИНТЕГРИРОВАНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ..................................................
39
ВАРИАНТЫ ЗАДАНИЙ ................................................................................................................ 40
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ........................................................................................... 60
5
ВВЕДЕНИЕ
Тема «Неопределенный интеграл» занимает особое место при
изучении курса математики и других дисциплин.
В данных методических указаниях рассматриваются основные
приемы интегрирования. Даны 30 вариантов заданий к типовому расчету
по 20 интегралов в каждом.
Приступая к вычислению интеграла, следует, прежде всего,
определить его тип и выбрать соответствующий метод интегрирования.
Окончательный результат рекомендуется проверять дифференциро-
ванием.
Прежде чем работать с данными методическими указаниями и
выполнять типовой расчет, следует проработать теоретический материал
по лекциям и по учебникам [I, гл. 10; 2, гл. 3, §22-26; 3, гл.5; 5, гл. 8].

6
1. ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Неопределенным интегралом от функции
()
xf
по переменной
x
называется совокупность всех ее первообразных. Записывается он в виде
()
dxxf
∫
, где
∫
– знак интеграла;
()
xf
– подынтегральная функция;
()
dxxf
– подынтегральное выражение (дифференциал функции);
x
–
переменная интегрирования.
Основные свойства неопределенного интеграла следующие:
()
CxFdxxf
+=
∫
)( , (1.1)
где
()
xF
– конкретная первообразная подынтегральной функции
()
xf
;
С
–
произвольная постоянная, которая является параметром семейства всех
первообразных функции
()
xf
;
()
(
)
()
xfdxxf
dx
d
=
∫
, (1.2)
∫
⋅∫
=
dxxfdxxf
)()(
γ
γ
, (1.3)
где
γ
– постоянная величина;
() ()( ) () ()
dxxfdxxfdxxfxf
2121
∫∫∫
+=+
, (1.4)
∫
+=
CxFxdF
)()(
. (1.5)
Замена переменной интегрирования. Если
() ()
CxFdxxf +=
∫
и
()
xuu =
– дифференцированная функция, то
() ()
CuFduuf +=
∫
или
()( ) () ()()
CxuFdxxuxuf +=
′
⋅
∫
. (1.6)
Отсюда имеем различные формы замены переменной интегриро-
вания:
()()() ()
duufdxxuxuf
∫∫
=
′
(внесение под знак дифференциала); (1.6.1)
() ()()()
dttxtxfdxxf
′
=
∫∫
(подстановка), (1.6.2)
где
()
tx – дифференцируемая функция.
7
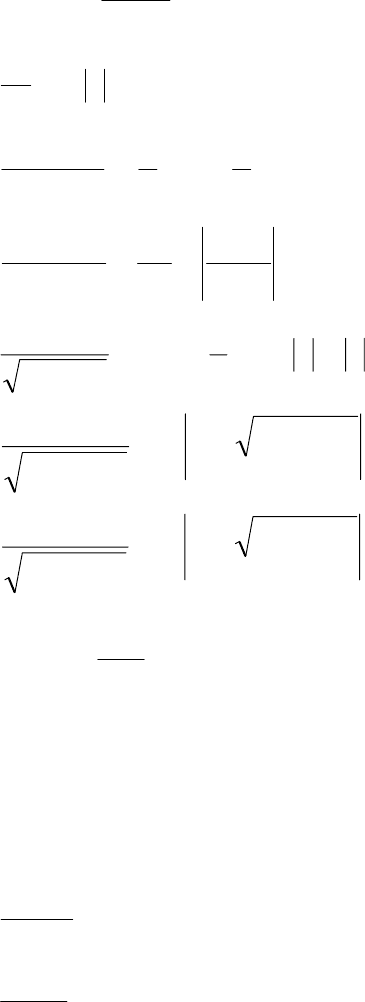
Интегрирование по частям:
∫∫
−= )()()()()()(
xduxvxvxuxdvxu
, (1.7)
где )(xu и )(xv – дифференцируемые функции.
2. ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
∫
+=
Cxdx
; (2.1)
C
m
x
dxx
m
m
+
+
=
+
∫
1
1
,
1−≠m
; (2.2)
Cx
x
dx
+=
∫
ln ; (2.3)
0,
1
22
≠+=
+
∫
aC
a
x
arctg
a
ax
dx
; (2.4)
C
ax
ax
a
ax
dx
+
+
−
=
−
∫
ln
2
1
22
,
0≠a
; (2.5)
xaC
a
x
xa
dx
>+=
−
∫
,arcsin
22
; (2.6)
0 ,ln
22
22
≠+++=
+
∫
aCaxx
ax
dx
; (2.7)
0 ,ln
22
22
≠+−+=
−
∫
aCaxx
ax
dx
(2.8)
0 ,
ln
>+=
∫
aC
a
a
dxa
x
x
; (2.9)
Cedxe
xx
+=
∫
; (2.10)
∫
+−=
Cxxdx
cossin
; (2.11)
∫
+=
Cxxdx
sincos
; (2.12)
Ctgx
x
dx
+=
∫
2
cos
; (2.13)
Cctgx
x
dx
+−=
∫
2
sin
; (2.14)

8
∫
+=
Cchxshx
; (2.15)
∫
+=
Cshxchx
; (2.16)
∫
+=
Cthx
xch
dx
2
; (2.17)
Cсthx
xsh
dx
+−=
∫
2
; (2.18)
CctgxecxC
x
tg
x
dx
+−=+=
∫
cosln
2
ln
sin
; (2.19)
CtgxxC
x
tg
x
dx
++=++=
∫
secln)
42
(ln
cos
π
. (2.20)
Общим способом интегрирования является сведение данного
интеграла к табличному с помощью равносильных преобразований
подынтегральной функции и использования указанных свойств
неопределенного интеграла.
В тексте буквой I обозначен рассматриваемый в примере интеграл.
Замечание. При встрече с действиями с произвольными постоянными
следует помнить следующее:
;
321
CCC
=±
321
CCC
=⋅
;
()
0,/
2321
≠=
CCCC
;
31
CmC
=±
;
31
CmC
=⋅
,
()
0≠m
;
()
0,/
31
≠=
mCmC
;
()
0,/
131
≠=
СCCm
,
и в областях определения и значения функций
()
xg
в общем будет
()
31
CCg
=
; где
321
,,
CCC
– произвольные постоянные, а m –
фиксированное число.
Замечание. Необходимо помнить, что интеграл от элементарной
функции не всегда является элементарной функцией. Так, например,
следующие интегралы не являются элементарными функциями:
dx
x
x
sin
∫
;
dx
x
x
cos
∫
;
dx
x
e
2
−
∫
;
dxx
2
sin
∫
;
dxx
2
cos
∫
;
x
dx
ln
∫
.
Для приближенного нахождения таких интегралов используют
функциональные ряды [2, гл. 4, §36; 3, гл. 9].

9
3. ТАБЛИЧНОЕ ИНТЕГРИРОВАНИЕ
Метод интегрирования состоит в сведении данного интеграла к
табличному с помощью алгебраических преобразований подынтегральной
функции, использования свойств неопределенного интеграла 1.3 и 1.4 и
таблицы интегралов. [1, гл.10, §2; 5, гл.8, §1].
П р и м е р 1. Найти интеграл .
9
24
xx
dx
+
∫
Р е ш е н и е. Умножим и поделим подынтегральную функцию на 9, затем
в числителе прибавим и отнимем
2
x
:
(
)
(
)
(
)
.
9
9
1
9
1
9
9
9
1
99
9
2222
22
22
x
dx
x
dx
dx
xx
xx
xx
dx
I
+
−=
+
−+
=
+
=
∫∫∫∫
Проверка:
.
9
1
)9(9
1
9
1
3
1
3
1
1
27
1
9
1
327
1
9
1
242222
xxxx
x
x
C
x
arctg
x
+
=
+
−=⋅
+
⋅−=
′
+−−
Это выражение совпадает с подынтегральной функцией,
следовательно, интеграл найден верно.
П р и м е р 2. Найти интеграл:
∫
⋅
.
cossin
22
xx
dx
Р е ш е н и е. Используем тождество:
1cossin
22
=+
xx
, затем произведем
почленное деление и применим свойство 1.4, формулы 2.18, 2.19,
получим:
.
sincoscossin
cossin
2222
22
Ссtgxtgx
x
dx
x
dx
dx
xx
xx
I
+−=+=
⋅
+
=
∫∫∫
Проверка:
xxxx
dx
dI
2222
cossin
1
sin
1
cos
1
⋅
=+=
.
.
327
1
9
1
C
x
arctg
x
I
+−−=
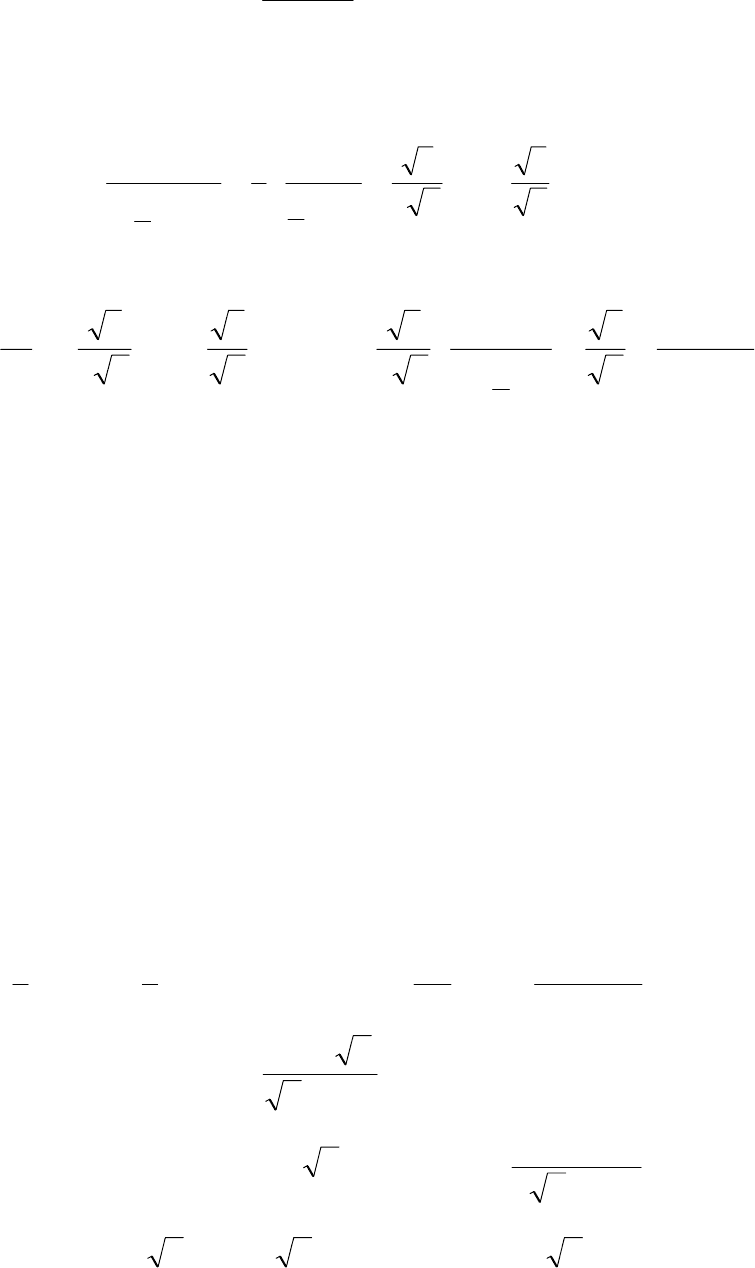
10
П р и м е р 3. Найти интеграл: .
32
2
∫
+
x
dx
Р е ш е н и е. Осуществим алгебраические преобразования, затем
используем свойство 1.3 и формулу 2.4:
.
2
3
23
3
3
2
3
1
3
2
3
2
2
Cxarctg
x
dx
x
dx
I +=
+
=
+
=
∫∫
Проверка: .
32
1
2
3
2
3
1
1
23
3
2
3
23
3
2
2
x
x
Cxarctg
dx
dI
+
=⋅
+
=
′
+=
Интеграл найден верно.
4. ЗАМЕНА ПЕРЕМЕННОЙ: ВНЕСЕНИЕ ПОД ЗНАК
ДИФФЕРЕНЦИАЛА
Метод состоит в использовании свойства 1.6 о замене переменной
интегрирования, которое записано в форме 1.6.1. Его суть состоит в
подборе такой дифференцируемой функции
()
xu
в данном интеграле, что
можно применить свойство 1.6.1 [5, гл. 8,§1; 4, гл. 9, §1].
П р и м е р 4. Найти интеграл
()
.1
8
32
dxxx
−⋅
∫
Р е ш е н и е. Взяв за ,1
3
−= xu
получим
dxxdu
2
3
=
, тогда
()()
()
.
27
1
27
11
3
1
3
1
9
39
3
8
38
C
x
C
u
xdxduuI
+
−
=+=−−∫=∫=
П р и м е р 5. Найти интеграл
()
.
1
dx
xx
xarctg
∫
+
.
Р е ш е н и е. Положив за
xarctgu
=
, имеем
()
,
12
xx
dx
du
+
=
тогда
() ()
∫∫
+=+===
,22
2
2
CxarctgCuxarctgdxarctguduI
()
.0
>
x
П р и м е р 6. Найти интеграл
()
.1
10
dxxx
−
∫
