Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

66 2 Particle Dynamics
2.4
(a) The force of contact F
c
between the blocks is equal to the force exerted on
m
2
:
F
c
= m
2
a (1)
where the acceleration of the whole system is
a =
F
m
1
+ m
2
(2)
∴ F
c
=
m
2
F
m
1
+ m
2
(b) Here the contact force F
c
is given by
F
c
= m
1
a =
m
1
F
m
1
+ m
2
Notice that F
c
= F
c
simply because m
1
= m
2
.
2.5
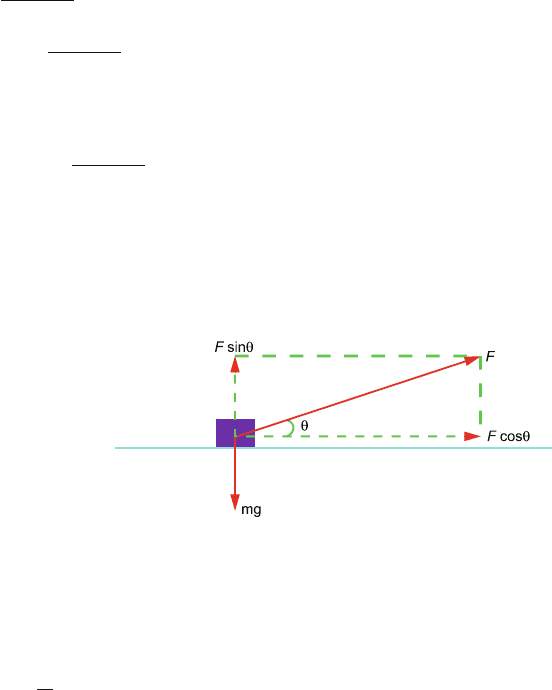
(a) When the box is dragged, the horizontal component of F is F cos θ and the
vertical component (upward) is F sin θ as in Fig. 2.19. The reaction force
N on the box by the floor will be
Fig. 2.19
N = mg − F sin θ (1)
(b) The equation of motion will be
ma = F cos θ − μN = F cos θ − μ(mg − F sin θ)
∴ a =
F
m
(cos θ + μ sin θ) − μg (2)
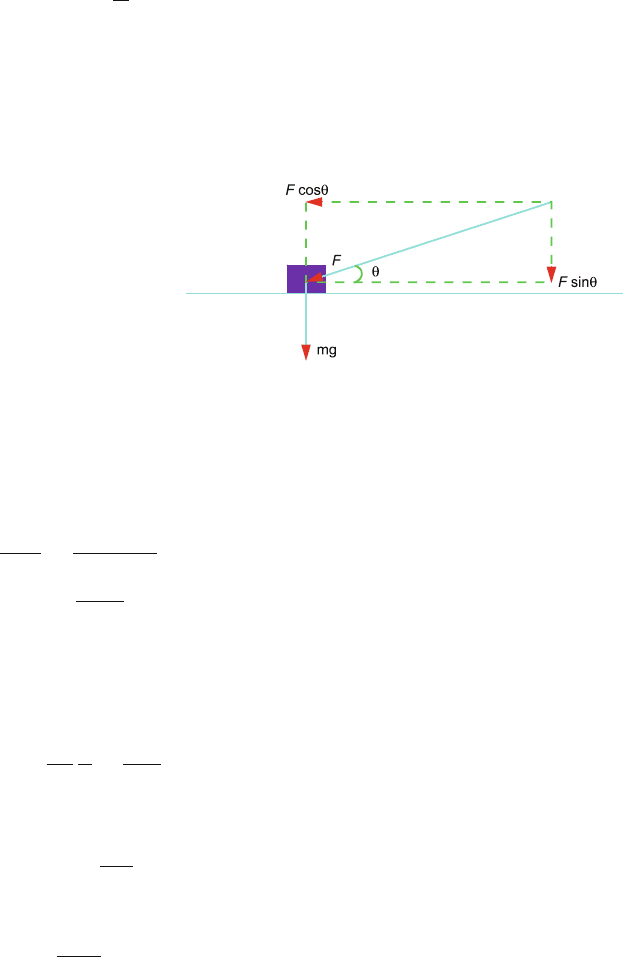
(c) When the box is pushed the horizontal component of F will be F cos θ and
the vertical component F sin θ (downwards), Fig. 2.20. The reaction force
exerted by the floor on the box will be
N
= mg + F sin θ (3)
which is seen to be greater than N (the previous case).
2.3 Solutions 67
The equation of motion will be
ma
= F cos θ − μN
= F cos θ − μ(mg + F sin θ)
∴ a
=
F
m
(cos θ − μ sin θ) − μg (4)
a value which is less than a (the previous case). It therefore pays to pull
rather than push at an angle with the horizontal. The difference arises due
to the smaller value of the reaction in pulling than in pushing. This fact
is exploited in handling a manual road roller or mopping a floor, which is
pulled rather than pushed.
Fig. 2.20
2.6 Let x be the length of the chain hanging over t he table. The length of the chain
resting on the table will be L − x. For equilibrium, gravitational force on the
hanging part of the chain = frictional force on the part of the chain resting on
the table. If M is the mass of the entire chain then
Mg x
L
=
M(L − x)
L
μg
∴ x =
μL
μ + 1
2.7 First method: The centre of mass of the hanging part of the chain is located at
a distance L/6 below the edge of the table, Fig. 2.21. The mass of the hanging
part of the chain is M/3. The work done to pull the hanging part on the table
W =
Mg
3
L
6
=
MgL
18
Second method: We can obtain the same result by calculus. Consider an element
of length dx of the hanging part at a distance x below the edge. The mass of the
length dx is
M dx
L
. The work required to lift the element of length dx through a
distance x is
dW =
M dx
L
gx
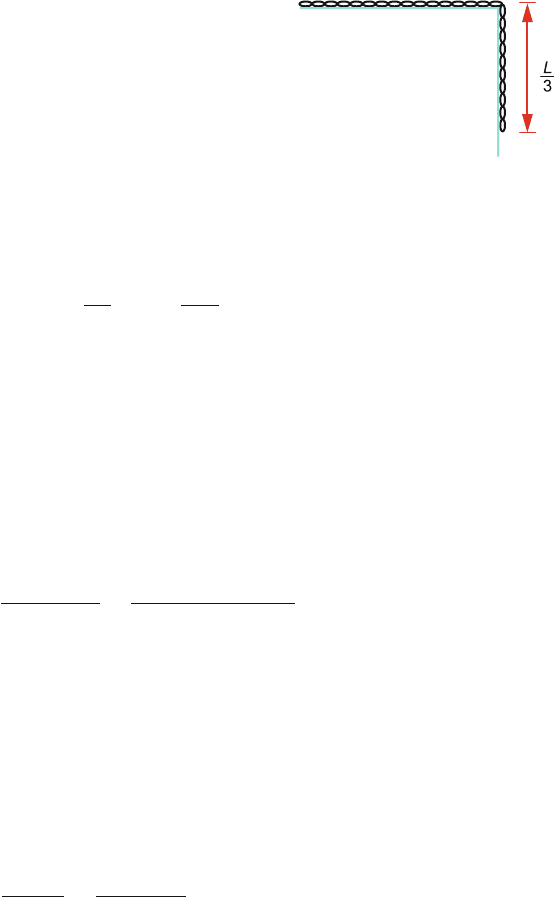
68 2 Particle Dynamics
Fig. 2.21
Work required to lift the entire hanging part is
W =
dW =
L/3
o
Mg
L
x d x =
MgL
18
2.8
(a) The equations of motion are
Ma = mg − T (1)
ma = T − Mgμ (2)
Solving (1) and (2)
a =
(m −μM)g
M + m
=
(0.45 − 0.2 × 2)9.8
2 + 0.45
= 0.2m/s
2
(b) T = m(g −a) = 0.45(9.8 − 0.2) = 4.32 N
(c) After 2 s, the velocity will be
υ
1
= 0 +at = 0.2 × 2 = 0.4m/s
1
When the string breaks, the acceleration will be a
1
=−μg =−0.2×9.8 =
−1.96 m/s
2
and final velocity v
2
= 0:
S =
v
2
2
− v
2
1
2a
1
=
0 − (0.4)
2
(2)(−1.96)
= 0.0408 m = 4.1cm
2.3.2 Motion on Incline
2.9
(a) Gravitational force down the incline is Mg sin θ. Frictional force up the
incline is μmg cos θ .Netforce

2.3 Solutions 69
F = μ Mg cos θ − Mg sin θ = Mg(μ cos θ −sin θ)
= 2 ×9.8
√
3
2
cos 30
◦
− sin 30
◦
= 4.9N
(b)
F
= Mg sin θ +μ Mg cos θ = Mg(sin θ + μ cos θ)
= 2 ×9.8
sin 30
◦
+
√
3
2
cos 30
◦
= 24.5N
2.10
y =
x
2
20
dy
dx
= tan θ =
x
10
For equilibrium, mg sin θ − μmg cos θ = 0
∴ tan θ = μ = 0.5
x = 10 tan θ = 10 ×0.5 = 5
y =
x
2
20
=
5
2
20
= 1.25 m
2.11
(a) μ = tan θ = tan 30
◦
= 0.577
(b) ma =−(mg sin θ +μ mg cos θ)
∴ a =−g(sin θ + μ cos θ) =−g(sin θ + tan θ cos θ)
=−9.8(2sin30
◦
) =−9.8
s =
v
2
0
−2a
=
(2.5)
2
2 × 9.8
= 0.319 m
Initial kinetic energy
K =
1
2
mv
2
0
Potential energy U = mgh = mgs sin θ
∴
U
K
=
2 mgs sin θ
mυ
2
0
=
2 × 9.8 × 0.319 × sin 30
◦
(2.5)
2
= 0.5
The remaining energy goes into heat due to friction.
(c) It will not slide down as the coefficient of static friction is larger than the
coefficient of kinetic friction.

70 2 Particle Dynamics
2.12 (a) The torque due to the external gravitational force on M
1
will be M
1
gr,
and the torque due to the external gravitational force on M
2
will be the
component of M
2
g along the s tring times r, i.e. (M
2
g sin θ)gr.Now,
these two torques act in opposite directions. Taking the counterclockwise
rotation of the pulley as positive and assuming that the mass M
1
is falling
down, the net torque is
τ = M
1
gr − (M
2
g sin θ)r = (M
1
− M
2
sin θ)gr (1)
and pointing out of the page.
(b) When the string is moving with speed υ, the pulley will be rotating with
angular velocity ω = v/r, so that its angular momentum is
L
pulley
= I ω =
Iv
r
and that of the two blocks will be
L
M
1
= rM
1
v L
M
2
= rM
2
v
All the angular momenta point in the same direction, positive if M
1
is
assumed to fall. The total angular momentum is then given by
L
total
= v
(M
1
+ M
2
)r +
I
r
(2)
(c) Using (1) and (2)
τ =
dL
dt
=
dυ
dt
(M
1
+ M
2
)r +
1
r
=
[
M
1
− M
2
sin θ
]
gr
The acceleration a =
dv
dt
=
[
M
1
− M
2
sin θ
]
g
(M
1
+ M
2
) +
1
r
2
2.13 (i) ma = F −mg sin θ (equation of motion, up the incline)
F = ma + mg sin θ = m(a + g sin θ)
= (1.0)(1 + 9.8 ×0.5) = 5.9N(θ = 30
◦
)
(ii) ma = F +mg sin θ (equation of motion, down the incline)
∴ F = ma − mg sin θ = m(a − g sin θ)
= (1.0)(1 − 9.8 ×0.5) =−3.9N
The negative sign implies that the force F is to be applied up the incline.
2.14 The displacement on the edge is measured by s while that on the floor by x.As
the mass m goes down the wedge the wedge itself would start moving towards

2.3 Solutions 71
left, Fig. 2.22. Since the external force in the horizontal direction is zero, the
component of momentum along the x-direction must be conserved:
Fig. 2.22
(M + m)
dx
dt
− m
ds
dt
cos α = 0(1)
Since the wedge is smooth, the only force acting down the plane is mg sin α
m
d
2
s
dt
2
−
d
2
x
dt
2
cos α
= mg sin α (2)
Differentiating (1)
(M + m)
d
2
x
dt
2
− m cos α
d
2
s
dt
2
= 0(3)
Solving (2) and (3)
d
2
s
dt
2
=
(M + m)g sin α
M + m sin
2
α
(acceleration of m)
d
2
x
dt
2
=
mg sin α cos α
M + m sin
2
α
(acceleration of M)
2.15 The lighter body of mass m
1
= m moves up the plane with acceleration a
1
and
the heavier one of mass m
2
= 3 m moves down the plane with acceleration
a
2
. Assuming that the s tring is taut, the acceleration of the two masses must
be numerically equal, i.e.
a
2
= a
1
= a. Let the tension in the string be T .
The equations of motion of the two masses are
F
1
= m
1
a
1
= ma = T − mg sin θ (1)
F
2
= m
2
a
2
= 3ma = 3mg sin θ − T (2)
Adding (1) and (2)
a =
g
2
√
2
(3)
72 2 Particle Dynamics
a
CM
=
m
1
a
1
+ m
2
a
2
m
1
+ m
2
=
a
1
+ 3a
2
4
(4)
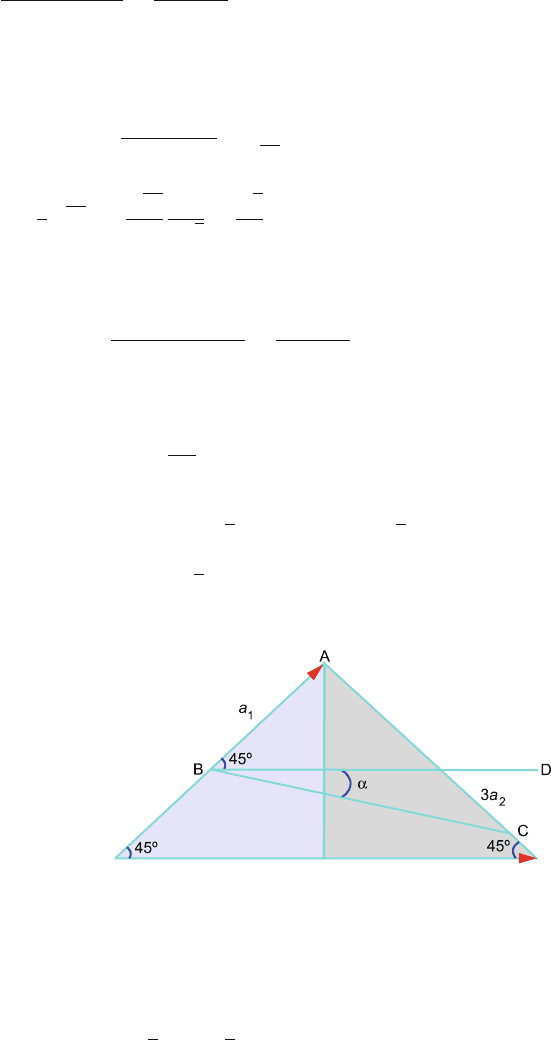
In Fig. 2.23 BA represents a
1
and AC represents 3a
2
. Therefore, BC the third
side of the ABC represents
|
a
1
+ 3a
2
|
. Obviously B
AC is a right angle so
that
|
a
1
+ 3a
2
|
= BC =
a
2
1
+ (3a
2
)
2
=
√
10a
∴ a
CM
=
1
4
√
10a =
√
10
4
g
2
√
2
=
√
5
8
g (5)
In Fig. 2.23, BD is parallel to the base s o that A
BD = 45
◦
. Let C
BD = α.
Now tan(α + 45
◦
) =
tan α +tan 45
◦
1 − tan α tan 45
◦
=
tan α +1
1 − tan α
(6)
Further, in the right angle triangle ABC,
tan
ABC = tan(α + 45
◦
) =
AC
AB
= 3(7)
Combining (6) and (7) tan α =
1
2
or α = tan
−1
1
2
.
Thus a
CM
is at an angle tan
−1
1
2
to the horizon.
Fig. 2.23
2.16
(a) Free body diagram (Fig. 2.24)
(b)
m
1
a = T
1
− m
1
g sin 30
◦
(1)
m
2
a = m
2
sin 60
◦
− T
2
(2)
(T
2
− T
1
)r = Iα =
1
2
Mr
2
a
r
(3)

2.3 Solutions 73
Fig. 2.24
(c) Combining (1), (2) and (3) and simplifying
a =
g
√
3m
2
− m
1
M + 2(m
2
+ m
1
)
2.17 Let m
1
= 2.1 kg and m
2
= 1.9 kg, Fig. 2.25. As the pulley is weightless the
tension is the same on either side of the pulley. Equations of motion are as
follows:
Fig. 2.25
m
1
a = m
1
g − T (1)
m
2
a = T −m
2
g (2)
Adding (1) and (2)
(m
1
+ m
2
)a = (m
1
− m
2
)g
∴ a =
(
m
1
− m
2
)
g
m
1
+ m
2
=
(2.1 − 1.9)9.8
2.1 + 1.9
= 0.49 m/s
2

74 2 Particle Dynamics
Distance travelled by either mass, s = 40 cm. Time taken
t =
2s
a
=
2 × 0.4
0.49
= 1.28 s.
2.18 Equations of motion are
ma
1
= mg sin θ − μmg cos θ (rough incline)
ma
2
= mg sin θ (smooth incline)
∴ a
1
= (sin θ − μ cos θ)g
a
2
= g sin θ
t
1
=
2s
a
1
t
2
=
2s
a
2
∴
t
1
t
2
=
4
3
sin θ
sin θ − μ cos θ
=
sin 45
◦
sin 45
◦
− μ cos 45
◦
=
1
√
1 − μ
∴ μ =
7
16
2.19 The normal reaction N = mg cos θ
Resultant downward force F = mg sin θ −μmg cos θ
Given that N = 2F
mg cos θ = 2 mg(sin θ − 0.5 cos θ)
∴ tan θ = 1 → θ = 45
◦
2.20 By prob. (2.17), each mass will have acceleration
a =
(m
1
− m
2
)g
m
1
+ m
2
The heaver mass m
1
will have acceleration a
1
vertically down while the lighter
mass m
2
will have acceleration a
2
vertically up:
a
2
=−a
1
The acceleration of the centre of mass of the system will be
a
CM
=
m
1
a
1
+ m
2
a
2
m
1
+ m
2
=
(m
1
− m
2
)a
1
m
1
+ m
2
∴ a
CM
=
(m
1
− m
2
)
2
g
(m
1
+ m
2
)
2
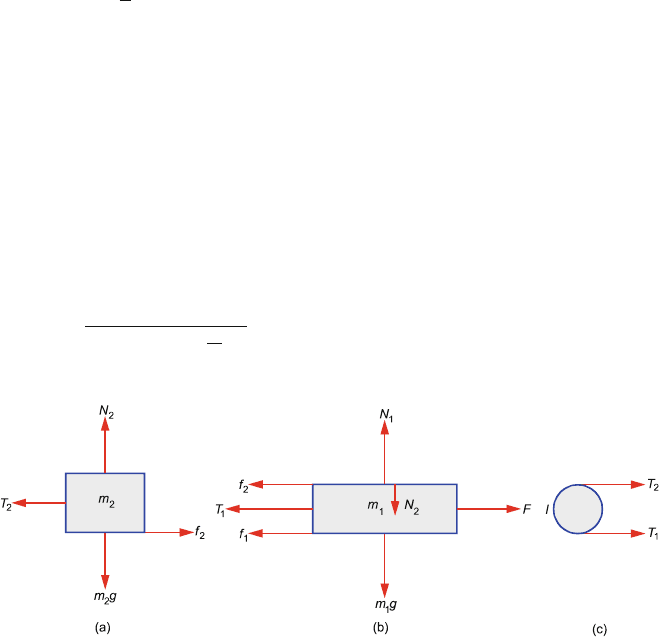
2.3 Solutions 75
2.21 Free body diagrams for the two blocks and the pulley are shown in Fig. 2.26.
The forces acting on m
2
are tension T
2
due to the string, gravity, frictional
force f
2
due to the movement of m
1
and the normal force which m
1
exerts on
it to prevent if from moving vertically. The forces on m
1
due to m
2
are equal
and opposite to those of m
1
on m
2
. By Newton’s third law the tensions T
1
and
T
2
in the thread are not equal as the pulley has mass. The equations of motion
for m
1
, m
2
and the pulley are
m
1
a = F − f
1
− f
2
− T
1
(1)
m
2
a = T
2
− f
2
(2)
α I = I
a
r
= r(T
1
− T
2
) (3)
Balancing the vertical forces
N
2
= m
2
g
N
1
= N
2
+ m
1
g = (m
1
+ m
2
) g
Frictional forces are
f
2
= μN
2
= μm
2
g (4)
f
1
= μN
1
= μ(m
1
+ m
2
)g (5)
Combining (1), (2), (3), (4) and (5), eliminating f
1
, f
2
and T
a =
F − μ(m
1
+ 3m
2
)g
m
1
+ m
2
+
I
r
2
Fig. 2.26
2.3.3 Work, Power, Energy
2.22
Net force F = F
1
+ F
2
= (
ˆ
i +2
ˆ
j +3
ˆ
k) + (4
ˆ
i −5
ˆ
j −2
ˆ
k)
= 5
ˆ
i −3
ˆ
j +
ˆ
k
