Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


86 2 Particle Dynamics
Eliminating p
H
between (1) and (2) and simplifying
P
L
=
2p
0
m
M + m
mv
L
=
2Mum
M + m
or v
L
=
2uM
M + m
= 2u (∵ m << M)
2.40 Let a body of mass m
1
moving with velocity u make a completely inelastic
collision with the body of mass m
2
initially at rest. Let the combined mass
moves with a velocity v
c
given by
v
c
=
m
1
u
m
1
+ m
2
=
u
2
(∵ m
1
= m
2
)
Energy lost =
1
2
mu
2
−
1
2
(2m)
u
2
2
=
1
4
mu
2
=
1
2
K
0
where K
0
=
1
2
mu
2
is the initial kinetic energy.
2.41 Let the speed of the bullet be u. Let the block + bullet system be travelling
with initial speed v.Ifm and M are the masses of the bullet and the block,
respectively, then momentum conservation gives
mu = (M + m)v (1)
∴ v =
mu
M + m
(2)
The initial kinetic energy of the block + bullet system
K =
1
2
(M + m)v
2
=
1
2
m
2
u
2
(M + m)
Work done to bring the block + bullet system to rest in distance s is
W = μ(M +m)gs =
1
2
m
2
u
2
(M + m)
∴ u =
(M + m)
m
2μ gs =
(2.000 + 0.005)
0.005
√
2 × 0.2 × 9.8 × 2
= 1123m/s
2.42 (a) Let m
1
= m with velocity u collide with m
2
= M, initially at rest. For
elastic collision the final velocities will be
v
1
=
(m
1
− m
2
)
m
1
+ m
2
u =
(m − M)
m + M
u (m < M) (1)
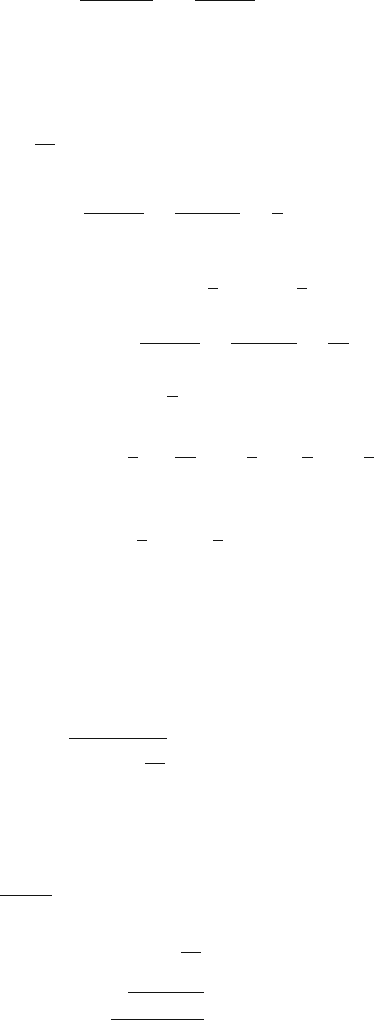
2.3 Solutions 87
v
2
=
2m
1
m
1
+ m
2
u =
2mu
m + M
(2)
By problem − v
1
= v
2
(3)
Combining (1), (2) and (3)
M
m
= 3(4)
(b) v
c
=
mu
M + m
=
mu
3m + m
=
u
4
(5)
(c) K
∗
= K
1
∗
+ K
2
∗
=
1
2
mv
1
∗2
+
1
2
Mv
2
∗2
But v
1
∗
=
Mu
M + m
=
3mu
3m + m
=
3u
4
v
2
∗
=−v
c
=−
u
4
∴ K
∗
=
1
2
m
3u
4
2
+
1
2
3m
u
4
2
=
3
8
mu
2
(d) K
1
(final) =
1
2
mv
2
1
=
1
8
mu
2
wherewehaveused(1)and(4).
2.43 We can work out this problem in the lab system. But we prefer to use the
centre of mass system. The CMS and LS scattering angles are related by
tan θ =
sin θ
∗
cos θ
∗
+
M
m
(1)
θ
max
is obtained from the condition
dtanθ
d θ
∗
= 0(2)
This gives cos θ
∗
=
m
M
(3)
∴ sin θ
∗
=
√
M
2
− m
2
M
(4)
88 2 Particle Dynamics
Use (3) and (4) in (1) to get
1 + cot
2
θ = cos ec
2
θ =
M
2
m
2
∴ sin θ
max
=
m
M
or θ
max
= sin
−1
m
M
2.44 Momentum of the bullet before collision = momentum of the block + bullet
system immediately after collision, Fig. 2.34:
Fig. 2.34
mv = (m + M)V (1)
where V is the i nitial speed of the block + bullet system. The kinetic energy
of the system immediately after the impact is
K =
1
2
(m + M)V
2
(2)
Due to the impact, the pendulum would swing to the right and would be raised
through the maximum height h vertically above the rest position of the pen-
dulum, Fig. 2.34. At this point, the kinetic energy of the pendulum is entirely
converted into gravitational potential energy:
1
2
(m + M)V
2
= (m + M)gh (3)
∴ V =
2gh (4)
Using (4) in (1)
v =
1 +
M
m
2gh (5)
2.3 Solutions 89
By measuring h and knowing m and M, the original velocity of the bullet can
be calculated.
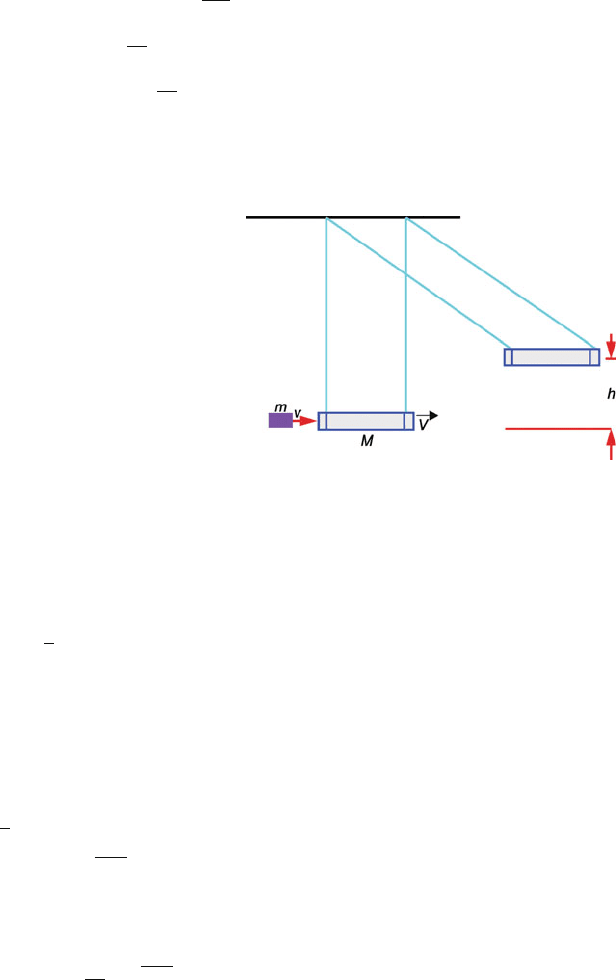
2.45 Let the area of the nozzle through where the jet comes be A m
2
. The mass of
water in the jet per second is ρ A v, where ρ is the density of water and v the
get velocity.
The momentum associated with this volume of water is
p = (ρ Av)v = ρ Av
2
(1)
The momentum after hitting the wall will also be equal to ρ Av
2
since the
collision is assumed to be elastic. Resolve the momentum along the x-axis
and y-axis, Fig. 2.35.
Fig. 2.35
The change of the x-component of momentum is
p
x
= p sin θ − (−p sin θ) = 2p sin θ (2)
The change in the y-component of momentum is
p
y
= p cos θ − p cos θ = 0(3)
Then p = p
x
= 2p sin θ = 2ρ A v
2
sin θ (4)
Pressure exerted on the wall will be
P =
p
A
= 2ρv
2
sin θ (5)
For normal incidence, θ = 90
◦
and
P = 2ρv
2
(6)

90 2 Particle Dynamics
2.46 For completely inelastic collision there is no r ebounding of the jet. The pres-
sure on the wall is given by
P = ρv
2
sin θ (1)
For normal incidence, θ = 90
◦
and
P = ρv
2
(2)
2.47 Resolve the momentum mv
1
and mv
2
along the original line of motion and
in a direction perpendicular to it. Along the original line of motion, the initial
momentum must be equal to the sum of the components of momentum after
the collision:
mv
0
= mv
1
cos 30
◦
+ mv
2
cos 30
◦
(1)
In the direction perpendicular to the original direction of motion, the sum of
components of momentum after the collision must be equal to zero because
before collision the balls do not have any component of momentum in the
perpendicular direction:
mv
1
sin 30
◦
− mv
2
sin 30
◦
= 0
or v
1
= v
2
(2)
This result could have been anticipated from symmetry.
Using (2) in (1)
v
0
= 2v
1
cos 30
◦
=
√
3v
1
or v
1
= v
2
=
v
0
√
3
=
9
√
3
= 5.19 m/s
Total kinetic energy of the two balls before collision
K
0
=
1
2
mv
2
0
+ 0 =
1
2
mv
2
0
(3)
Total kinetic energy after the collision
K
=
1
2
mv
2
1
+
1
2
mv
2
2
= mv
2
1
=
1
3
mv
2
0
(4)
On comparing (3) and (4) we conclude that kinetic energy is not conserved.
The collision is said to be inelastic.

2.3 Solutions 91
2.48 Time taken for the ball to reach the plane in the initial fall
t
0
=
2h
g
(1)
Velocity with which it reaches the plane
u
1
=
2gh (2)
The velocity with which it rebounds from the plane
v
1
= eu
1
= e
2gh (3)
Time to reach the plane again
t
1
=
2v
1
g
= 2e
2h
g
= 2et
0
If this process is repeated indefinitely the total time
T = t
0
+ t
1
+ t
2
+···+t
∞
= t
0
+ 2et
0
+ 2e
2
t
0
+···
= t
0
[1 + 2e(1 + e +e
2
+···)]
= t
0
1 +
2e
1 − e
=
2h
g
1 + e
1 − e
where we have used the formula for the sum of infinite number of terms of a
geometric series.
2.49 Total distance traversed
S = h +2h
1
+ 2h
2
+··· =h +2e
2
h + 2e
4
h + 2e
6
h +···
= h
1 +
2e
2
1 − e
2
= h
(1 + e
2
)
1 − e
2
2.50
On the first bounce,v
1
= e
2gh
On the second bounce,v
2
= e
2
2gh
On the nth bounce,v
n
= e
n
2gh
h
n
=
v
2
n
2g
= e
2n
h
92 2 Particle Dynamics
2.51 Let the two bodies of mass m
1
and m
2
be travelling with the velocities u
1
and
u
2
before the impact, and the combined body of mass m
1
+ m
2
with velocity
v after the impact is
v =
m
1
u
1
+ m
2
u
2
m
1
+ m
2
(1)
Energy wasted = total kinetic energy before the collision minus total kinetic
energy after the collision
W =
1
2
m
1
u
1
2
+
1
2
m
2
u
2
2
−
1
2
(m
1
+ m
2
)v
2
=
1
2
m
1
u
1
2
+
1
2
m
2
u
2
2
−
1
2
(m
1
u
1
+ m
2
u
2
)
2
m
1
+ m
2
=
1
2
m
1
m
2
m
1
+ m
2
(u
1
− u
2
)
2
2.52 Resolve the momentum along x- and y-axes at points A and B, Fig. 2.36.Take
the downward direction as positive:
p
x
(A) = p cos θ p
x
(B) = p cos θ
p
y
(A) =−p sin θ p
y
(B) = p sin θ
Then p
x
= p
x
(B) − p
x
(A) = p cos θ − p cos θ = 0
p
y
= p
y
(B) − p
y
(A) = p sin θ − (−p sin θ) = 2p sin θ
∴ p = p
y
= 2p sin θ
Fig. 2.36
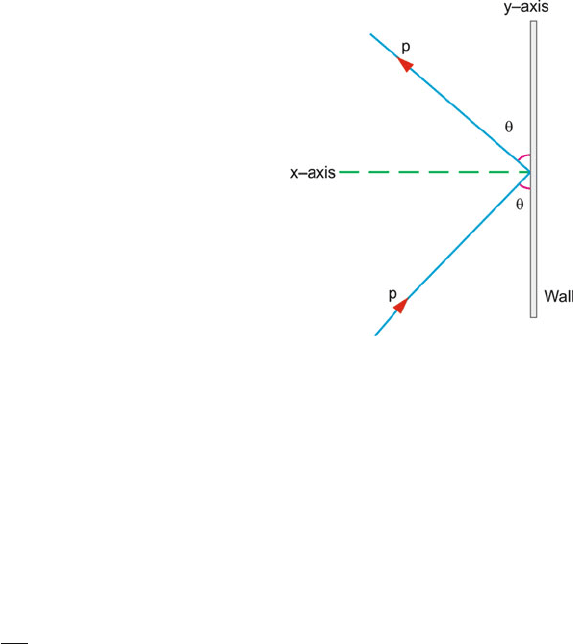
2.53 Let the shell of mass 2m explode into two pieces each of mass m.Atthe
highest point the entire velocity consists of the horizontal component (v cos θ)
alone. Since one of the components retraces its path, it follows that it has
velocity −v cos θ, and therefore a momentum −mv cos θ. Let the momentum
of the other pieces be p. Now, the momentum of the shell just before the
explosion was 2mv cos θ momentum conservation gives

2.3 Solutions 93
p − mv cos θ = 2mv cos θ
∴ p = 3mv cos θ
∴ velocity =
p
m
= 3v cos θ
2.54 Volume of air moving down per second = Av, where v is the air velocity
moving down through an area A.
Mass of air moving down per second = ρ Av
F =
p
t
=
mass
sec
(v) = ρ Av
2
Reaction force upward = Helicopter’s weight
ρ Av
2
= Mg
v =
Mg
ρ A
=
500 × 9.8
1.3 × 45
= 9.15 m/s
2.55 If v is the velocity of each bullet of mass m and n the number of bullets that
can be fired per second then rate of change of momentum will be
p
t
= mnv (1)
∴
p
t
= F = mnv (2)
n =
F
mv
=
150
(0.1)(1000)
= 1.5/s
Thus the number of bullets that can be fired per minute will be 60 ×1.5 = 90.
2.56 If v is the velocity with which a particle of mass m falls on the balance pan,
momentum before impact is mv and after impact −mv so that
p =−mv − mv =−2mv (1)
If height of fall is h then
v =
2gh =
√
2 × 9.8 × 1.6 = 5.6m/s(2)

94 2 Particle Dynamics
If n particles fall per second, the force exerted on the pan is
F =+2mnv = (2)(0.1)
441
60
(5.6) = 8.232 N
=
8.232
9.8
kg wt = 0.84 kg wt
2.57 In this case, the particles will stick to the pan. Therefore the scale reading will
increase due to the weight of the particles that get accumulated in the pan.
For complete inelastic collision p = mv as the final momentum is zero. Net
force on the scale = weight of the particle + force of impact. At time t, scale
reading (in newtons)
= mngt + mn
2gh
= mng
t +
2h
g
!
Scale reading in kg wt = mn
t +
2h
g
!
2.58 Let a sphere of mass m
1
travelling with velocity u
1
collide with the second
sphere of mass m
2
at rest, with their centres in straight line. After the collision
let the final velocities be v
1
and v
2
, respectively, for m
1
and m
2
. By definition
the coefficient of restitution e is given by the ratio
e =
Relative velocity of separation
Relative velocity of approach
=
v
2
− v
1
v
1
(1)
Momentum conservation requires that total momentum before collision =
total momentum after collision:
m
1
u
1
= m
1
v
1
+ m
2
v
2
(2)
Eliminating v
2
between (1) and (2),
v
1
=
(m
1
− em
2
)u
1
m
1
+ m
2
(3)
v
2
=
m
1
(1 + e)u
1
m
1
+ m
2
(4)
(i) Putting u
1
= u, m
1
= m and m
2
=
m
2
v
1
=
u
3
(2 − e) (5)
v
2
=
2u
3
(1 + e) (6)
2.3 Solutions 95
Total energy after the collision
K
= K
1
+ K
2
=
1
2
mv
2
1
+
1
2
m
2
v
2
2
(7)
Using (5) and (6) in (7) and simplifying
K
=
mu
2
6
(2 + e
2
) (8)
(ii) Kinetic energy lost during the collision
K = K
0
− K
=
1
2
mu
2
−
mu
2
6
(2 + e
2
) =
mu
2
6
(1 − e
2
)
2.59
(a) Distance traversed by the car before it falls off, s = 18 − 2 = 16 m:
t =
2s
a
=
2 × 16
4
= 2
√
2s
(b) By Newton’s third law, the force exerted by the car is equal to that by
boat + car
(M + m)a
B
= ma
where M = 8000 kg, m = 1200, a = 4m/s
2
The acceleration of the boat a
B
=
ma
M+m
= 0.26 m/s
2
The distance travelled by the boat in the opposite direction
s
B
=
1
2
a
B
t
2
=
1
2
× 0.26 ×
2
√
2
2
= 104 m
(c) Momentum conservation gives
mv
c
= (M + m)v
B
v
B
v
C
=
m
M + m
=
1200
8000 + 1200
= 0.13
which is independent of the car’s acceleration.
2.3.5 Variable Mass
2.60
(a) Resultant force on rocket = (upward thrust on rocket) − (weight of
rocket)
∴ m
dv
dt
=−v
r
dm
dt
− g (1)
