Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book

Подождите немного. Документ загружается.

550 12 Electric Circuits

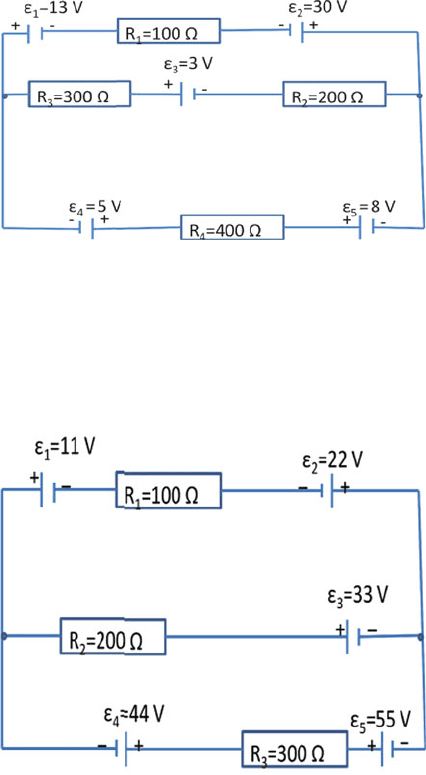
12.51 Apply Kirchhoff’s rules to the circuit shown in Fig. 12.25 to produce three

equations with three unknown branch currents. You do not have to solve

these equations for individual current.

[University of Aberystwyth, Wales 2008]

Fig. 12.25

12.52

(i) State Kirchhoff’s two rules

(ii) Apply Kirchhoff’s rules to the circuit shown in Fig. 12.26 to produce

three equations with three unknown branch currents. You do not have to

solve these equations for individual current.

[University of Aberystwyth, Wales 2007]

Fig. 12.26

12.53 Figure 12.27 shows a series parallel resistive circuit connected to a dc supply.

For the circuit shown work out the following:

(i) The voltages V

, V

across resistors R

and R

(ii) The voltage V

across resistors R

and R

(iii) The currents I

, I

and I

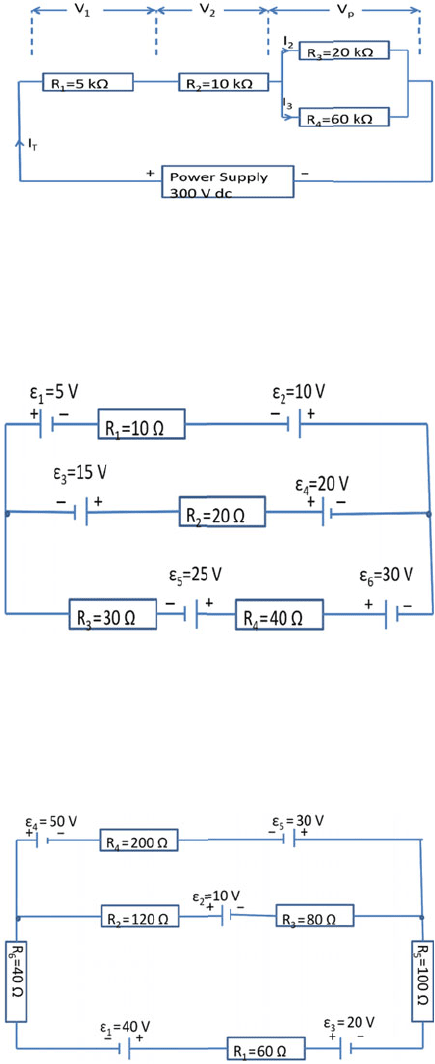
12.2 Problems 551

Fig. 12.27

12.54 Apply Kirchhoff’s rules to the circuit shown in Fig. 12.28 to produce three

equations with three unknown branch currents. You do not have to solve

these equations for individual I.

[University of Aberystwyth, Wales 2006]

Fig. 12.28

12.55 Apply Kirchhoff’s rules to the circuit shown in Fig. 12.29 and present the

simultaneous equations necessary to calculate the currents in each of the

branches of the circuit. You do not have to solve these equations for the

branch currents.

Fig. 12.29

552 12 Electric Circuits

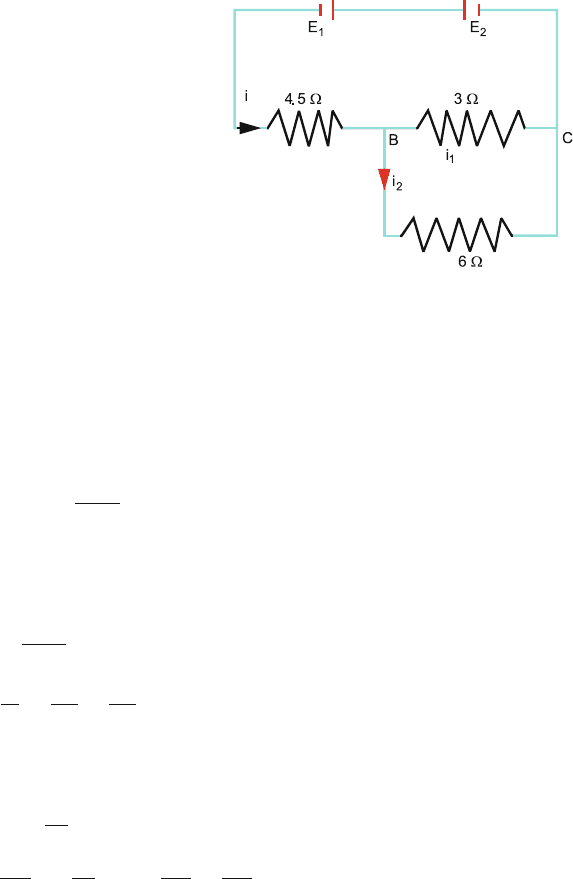
12.56 In the circuit shown in Fig. 12.30, the cells E

and E

have emfs 4 and 8 V

and internal resistances 0.5 and 1 , respectively. Calculate the current in

each resistor and the potential difference across each cell.

[Indian Institute of Technology 1973]

Fig. 12.30

12.3 Solutions

12.3.1 Resistance, EMF, Current, Power

12.1 In the segment ACD, the two 3  resistances give 6, which with 6  in

parallel yields

6 × 6

6 + 6

= 3 . This together with 3 , across DE in series, gives

6  which together with 6  across AE in parallel gives 3 . By a similar

reasoning resistance along AFB is 6 , which with 3 , across AB in parallel

yields the effective resistance across AB:

6 × 3

6 + 3

= 2 

12.2

R =

ρl

where v

is the constant volume. Change in the resistance

R = 2ρl

l

∴

R

≡ 2

l

≡ 2 ×

0.1

100

0.2

100

or 0.2%

12.3 Solutions 553

12.3 Let the resistances be R

and R

+ R

= p (series) (1)

+ R

= q (parallel) (2)

Combining (1) and (2)

− R

=±



n(n − 4)

Since R

and R

are real, n ≥ 4.

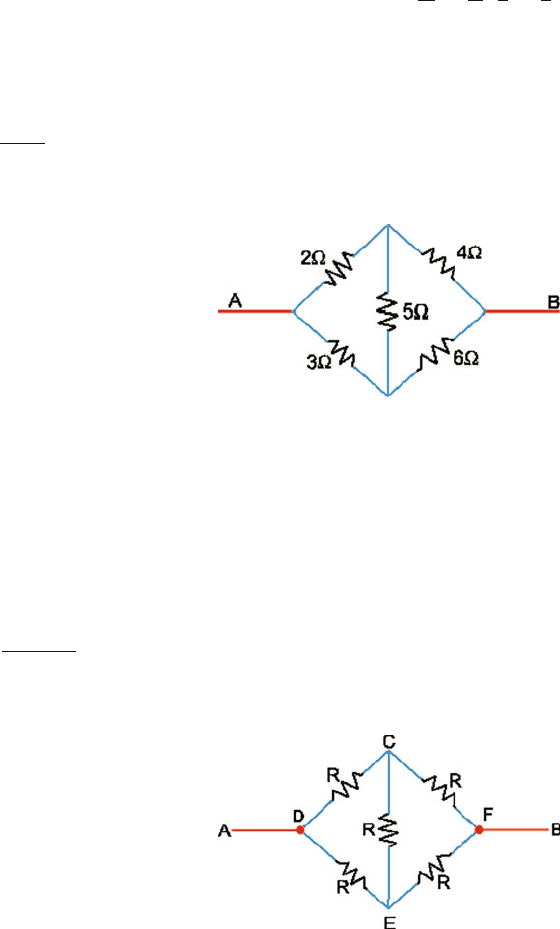
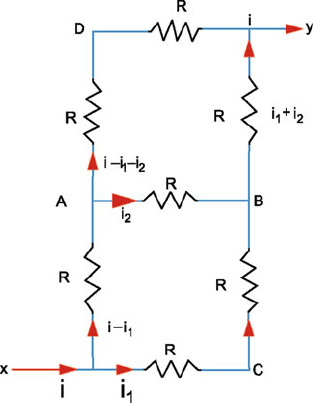
12.4 Let a current i enter at A and leave at C. Currents in various branches are

given by the junction theorem, Fig. 12.31. The potential difference

+ V

= V

∴ 3i

+ 5i

= 6(i −i

)

or 9i

+ 5i

= 6i (1)

= V

+ V

= V

+ V

∴ 3i

+ 2(i

−i

) = 6(i −i

) + 4(i −i

)

or 15i

− 6i

= 10i (2)

Solving (1) and (2), i

= 0. Thus the middle branch BD is rendered ineffec-

tive.

Two resistances of 3 and 2  in series in the upper branch are to be combined

in parallel with two other resistances of 6 and 4  in series in the lower branch

to obtain the effective resistance between A and C. This is given by

eff

(3 + 2)(6 + 4)

(3 + 2) + (6 + 4)

= 3.33 

Fig. 12.31

554 12 Electric Circuits

This particular problem could have been easily solved by noticing that Wheat-

stone bridge balance requirement is fulﬁlled since P/Q = R/S; here 3/2 =

6/4, in which case the current in the middle branch is zero (see prob. 12.33).

12.5 The network in Fig. 12.3 can be recast as shown in Fig. 12.32.Hereagain

the balancing condition for Wheatstone bridge is satisﬁed:

Therefore the middle branch resistor of 5  is rendered ineffective. The total

resistance in the upper branch is 2 +4 = 6  and in the lower branch 3 +6 =

9 . The equivalent resistance for 6 and 9  in parallel will be

6 × 9

6 + 9

= 3.6 

Fig. 12.32

12.6 For convenience the given network can be recast as in Fig. 12.33. It is seen

that this network is exactly identical with that in prob. (12.5) in which the

Wheatstone bridge condition is satisﬁed. Therefore, the resistance in the mid-

dle branch CE is rendered ineffective. The total resistance in the upper branch

is obviously equal to 2R which is also the case for the lower branch.

Therefore, the effective resistance between D and F will be

eff

2R × 2R

2R + 2R

= R

Fig. 12.33

12.3 Solutions 555

12.7 Let R

be the equivalent resistance of the circuit. Let a current i enter at X

and emerge at Y. The distribution of currents in various branches is shown in

Fig. 12.34. The potential drop across X and Y

= iR

(1)

Now V

= V

+ V

= R(i −i

) + 2R(i − i

−i

) = 3Ri − 3Ri

− 2Ri

(2)

From (1) and (2)

= R(3i −3i

− 2i

) (3)

and i

can be expressed in terms of i:

= V

+ V

= V

+ V

∴ 2Ri

= R(i −i

) + Ri

or 3i

−i

= i (4)

Also, V

= V

+ V

= V

+ V

∴ Ri

+ R(i

) = 2R(i − i

−i

)

or 3i

+ 4i

= 2i (5)

Solving (4) and (5), i

= 2i/5 and i

= i/5.

Using the values of i

and i

in (3) we ﬁnd R

= 7R/5.

Fig. 12.34

556 12 Electric Circuits

12.8

(i) Let the current in AD, DE and R be i

, i

and i

, respectively:

= 5 −2 = 3 A (by junction theorem)

= V

+ V

∴ i

× 6 = 5 × 4 + 5 ×2

∴ i

= 5A

∴ i

= 2 +5 = 7A

= V

+ V

3R = 2 × 5 + 7 × 5

∴ R = 15 

(ii) V

= V

+ V

= 4 ×5 +15 × 3 = 65 V

(iii) Heat developed per second = power =



= 5

× 4 + 2

× 5 + 5

× 6 + 3

× 15 + 7

× 5

= 650 J/s = 650/4.18 Cal/s = 155.5Cal/s

12.9 The combination of 3 and 7  resistance in series is 10 . This in parallel with

10  resistance yields 5 . This in series with another 5  resistance gives

the combined resistance of 10 . This being in parallel with 10  resistance

across A and B gives the effective resistance of 5  across A and B.

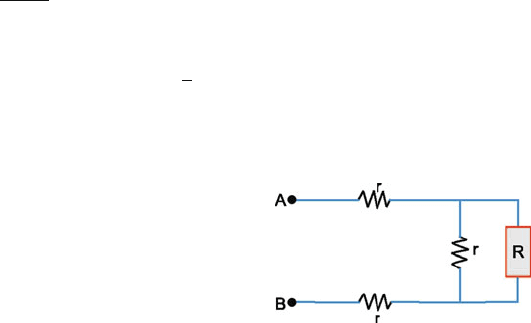
12.10 Let the effective resistance between A and B be R. Then by adding one

more section to inﬁnite sections of resistors, the effective resistance will not

change, Fig. 12.35.

The middle r is in parallel with R and the other two r’s are in series. Then

R = r +

R +r

Simplifying R

− 2Rr − 2R

= 0

whose solution is R = r



1 +

√



The second solution is ignored since R must be positive.

Fig. 12.35

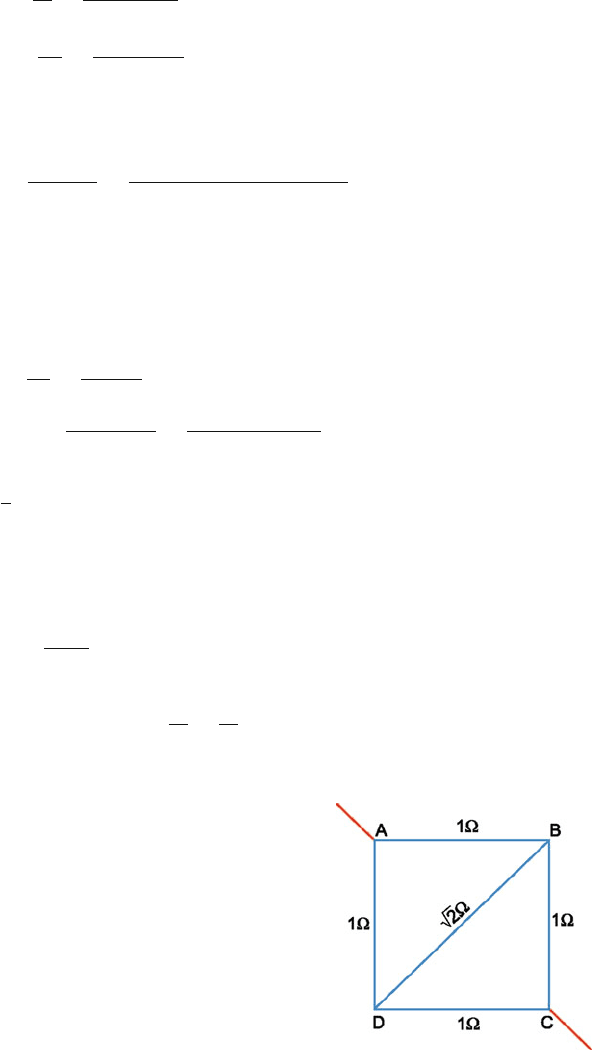
12.3 Solutions 557

12.11

ρl

10 × 10

−6

π(0.05)

= 1.274 ×10

−3



49 × 10

−6

π(0.05)

= 6.24 ×10

−3

In parallel arrangement

R =

+ R

(12.739 × 62.42) × 10

−6

(12.739 + 62.42) × 10

−3

= 10.58 ×10

−3

l = 2 

∴ l = 1890 cm = 18.9m

12.12

= R

(1 + αt

)

= R

(1 + αt

)

∴

1 + αt

∴ α =

− R

− t

)

25.7 − 20.0

20 × (100 − 25)

= 3.8 ×10

−3

◦

12.13 Resistance of each side = 10 × 0.1 = 1 . Resistance of the diagonal =

√

2 .TheP.D.,V

= V

as R

= R

. Hence no current ﬂows

through the diagonal BD, Fig. 12.36. The effective resistance of the network

is obtained by combining the resistance of AB and BC in series (1 + 1) in

parallel with that of AD and DC in series (1 +1):

eff

2 × 2

2 + 2

= 1 

Power dissipated P =

= 4W.

Fig. 12.36

558 12 Electric Circuits

12.14

R =

(100)

= 166.7 

R = R

(1 + αt)

t =

R − R

166.7 − 20

20 × 0.0052

= 1410

◦

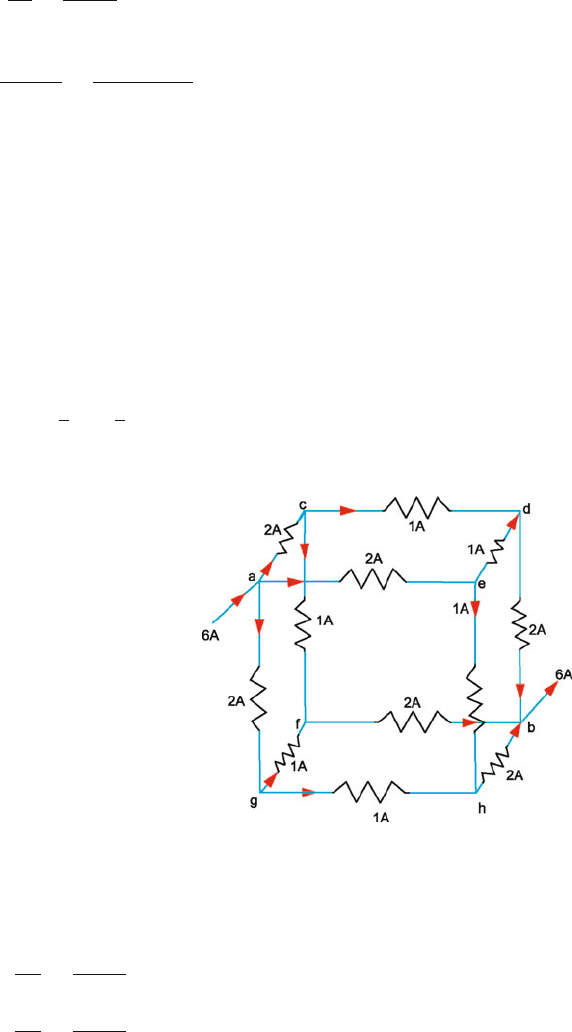
12.15 Let a current of 6 A be sent through the corner a. Let a potential difference

be established between a and b and current 6 A ﬂow out from b. The

currents in various branches are indicated in Fig. 12.37 from symmetry con-

siderations. If R

is the equivalent resistance of this network across the body

diagonal ab

= 6 R

But V

= V

+ V

= 2R + R + 2R = 5R

∴ 6 R

= 5R

or R

R =

× 10 = 8.33 

Fig. 12.37

12.16 W = V

(220)

= 1936 

(220)

100

= 484 

12.3 Solutions 559

Joule heat in R

, H

= i

= 1936 i

Joule heat in R

, H

= i

= 484 i

Therefore, 25 W bulb glows brighter.

12.17 By prob. (12.16), R

= 1936  and R

= 484 :

= i

V =

iV R

+ R

= i

V =

iV R

+ R

Therefore, 100 W bulb glows brighter.

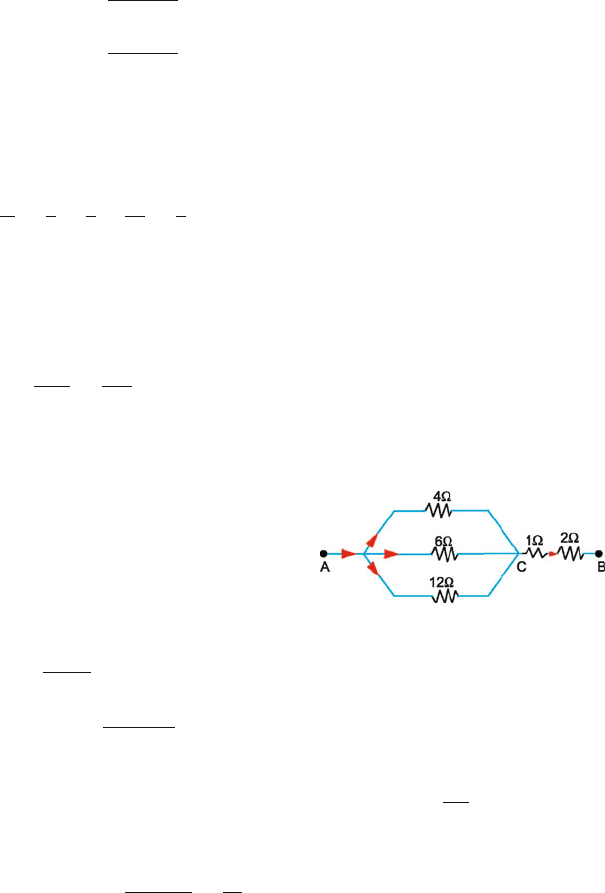
12.18 Effective resistance in parallel is given by (Fig. 12.38)

∴ R = 2 

Total resistance, R

= 2 +1 +2 = 5 

Current in the circuit

i =

120

= 24 A

= iR

= 24 ×2 = 48 V.

Fig. 12.38

12.19

i =

R +r

P = i

R =

(R +r)

Maximum power delivered to R is obtained by setting

∂ P

∂ R

= 0. This gives

R = r:

∴ P

max

(r +r)