Калин Б.А. Физическое материаловедение. Том 1. Физика твердого тела

Подождите немного. Документ загружается.

Порядок группы n = 24, число классов сопряженных элементов

k = 5. Генераторы группы

[

]

001

C и

[

]

111

C .

Из таблиц для групп

T и O видно, что равенство углов поворота

является необходимым, но не достаточным условием вхождения в

один класс сопряженных элементов. Действительно, элементы

симметрии, соответствующие поворотам на 120° вокруг осей <111>

в группе

T входят в два класса сопряженных элементов, а в группе

O − в один.

Рассматривая комбинации поворотных и инверсионных осей,

получим еще 21 точечную группу (

группы второго рода), таким

образом, возможно существование 32 точечных групп.

В группе

m 3 m (O

) 48 элементов, 10 классов сопряженных эле-

ментов. Генераторы группы , и

]001[

]111[

C 1 .

В табл. 1.3 приведены все кристаллографические точечные

группы и некоторые их характеристики. Если плоскость симметрии

m перпендикулярна главной оси N, то это обозначается как

(или

N/m), если ось N лежит в этой плоскости, то − Nm. Если главная ось

вертикальна, то по Шенфлису первые группы имеют обозначения

(h − горизонтальная плоскость), вторые − C

(v − вертикальная

плоскость).

В обозначениях по Шубникову знак умножения между элемен-

тами симметрии означает их параллельность, знак деления − пер-

пендикулярность, косая черта − косое расположение этих элемен-

тов.

В таблице приведены также «формулы симметрии», где исполь-

зованы обозначения:

L − оси симметрии, C − центр симметрии, P −

плоскость симметрии; перед каждым символом стоит число соот-

ветствующих элементов.

Стереографические проекции элементов симметрии для групп

23(T), 432(O) и m 3 m(O

) приведены на рис. 1.43.

Кроме деления на сингонии 32 класса симметрии можно груп-

пировать по более крупным подразделениям.

Таблица 1.3

Распределение кристаллических классов (точечных групп)

по сингониям

Сингонии

Обозначение

международное

Обозначение

по

Шубникову

Обозначение

по

Шенфлису

Формула

симметрии

Триклинная 1

= S

Моноклинная 2

2 : m

= C

Ромбическая

(орторомбическая)

222

mm2

mmm

: 2

2 · m

· 2 : m

= V

3PC

Тетрагональная 4

422

4mm

/mmm

: 2

4 : m

· m

· 4 : m

· m

= V

5PC

L 2L

Ромбоэдрическая

(тригональная)

3 m

: 2

3 · m

· m

= S

3PC

Гексагональная

6 m2

622

6mm

/mmm

: m

· 3 : m

: 2

6 : m

· m

· 6 : m

7PC

Кубическая 23

4 3m

432

3 m

3/ 4

3/4

3PC

L 6P

9PC

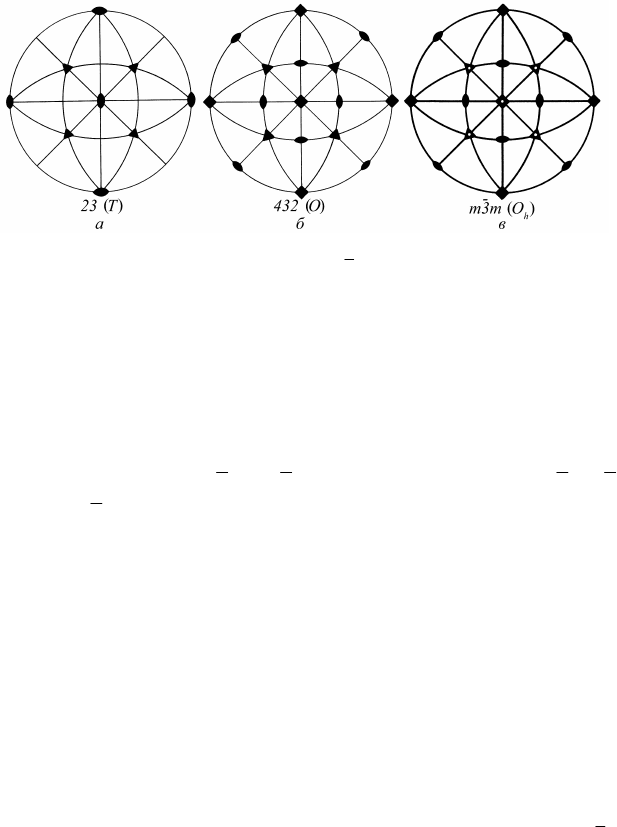
Рис. 1.43. Стереографические проекции элементов симметрии групп

23(T), 432(O) и m 3m(O

)

Наличие или отсутствие центра симметрии

. В классах с цен-

тром симметрии не может быть полярных направлений, а значит,

не может быть и физических свойств, характеризуемых полярной

симметрией (пироэлектричество, пьезоэлектричество).

В дифракционных методах исследования особенно выделяют

классы симметрии, содержащие центр симметрии, их называют

лауэвскими классами: m 3m, m 3 , 6/mmm, 6/m, 4/mmm, 4/m, 3m, 3 ,

mmm, 2/m, 1 . Таким образом, существует 11 лауэвских классов.

Энантиоморфизм. Два объекта, описываемые группой симмет-

рии, содержащей операции только первого рода, и зеркально рав-

ные друг другу, называются энантиоморфными. Для описания при-

надлежности объектов к правой или левой энантиоморфной разно-

видностям пользуются также термином «хиральность». К энантио-

морфным классам относятся 11 классов с поворотными элементами

симметрии:

1, 2, 3, 4, 6, 23, 222, 32, 622, 422, 432.

Простой формой кристалла называется многогранник, все грани

которого можно получить из одной грани с помощью преобразова-

ний симметрии, свойственных точечной группе симметрии данного

кристалла.

Простыми формами, принадлежащими кристаллам класса

m 3 m

при выборе грани (111), (100) или (110) являются октаэдр, куб и

ромбический додекаэдр.

Решетки Бравэ. О. Бравэ показал, что все многообразие кри-

сталлических структур можно описать с помощью 14 типов

решеток, по формам элементарных ячеек и по симметрии и подраз-

деляющихся на 7 кристаллографических сингоний. Эти решетки

были названы

решетками Бравэ. Любую кристаллическую струк-

туру можно представить с помощью одной из решеток Бравэ. Для

выбора

ячейки Бравэ используют три условия:

1) симметрия элементарной ячейки должна соответствовать

симметрии кристалла, точнее, наиболее высокой симметрии той

сингонии, к которой относится кристалл. Ребра элементарной

ячейки должны быть трансляциями решетки;

2) элементарная ячейка должна содержать максимально воз-

можное число прямых углов или равных углов и равных ребер;

3) элементарная ячейка должна иметь минимальный объем.

Эти условия должны выполняться последовательно, т.е. при вы-

боре ячейки первое условие важнее второго, а второе важнее

третьего.

По характеру взаимного расположения основных трансляций

или по расположению узлов все кристаллические решетки разби-

ваются, по Бравэ, на четыре типа:

примитивные (

P),

базоцентрированные (

C, B или A),

объемно-центрированные (

гранецентрированные (

F).

Таблица 1.4

Распределение ячеек Бравэ по сингониям

Сингонии Ячейки

Бравэ

Сингонии Ячейки

Бравэ

Триклинная P Тетрагональная P

Моноклинная P

Ромбоэдрическая

(тригональная)

Гексагональная P Ромбическая

(орторомбическая)

Кубическая P

В примитивной ячейке узлы решетки располагаются только в

вершинах ячейки, а в сложных ячейках имеются еще дополнитель-

ные узлы. В объемноцентрированной I-ячейке − один узел в центре

ячейки, в гранецентрированной

F-ячейке по одному узлу в центре

каждой грани, в базоцентрированной

C (A, B)-ячейке − по одному

узлу в центрах пары параллельных граней.

Распределение ячеек Бравэ по сингониям показано в табл. 1.4.

1.3.6. Пространственные группы

Пространственной группой кристалла называются всевозмож-

ные преобразования кристаллического пространства, которые пе-

реводят каждую его точку и каждое направление в эквивалентные

им точки и направления.

Элементы этой группы осуществляют преобразования вида

r′ = Rr + t, (1.97)

где

R − одна из операций поворота (собственного или несобствен-

ного);

r − операция переноса (трансляции). Обычно это преобразо-

вание записывают в виде

r′ = {R/t} r. (1.98)

При det

R = +1 элементы {R/t} описывают винтовое движение,

им отвечают

винтовые оси симметрии; при detR = −1 эти элементы

описывают отражение в плоскости со смещением в направлении

вектора трансляции

t, им отвечают плоскости скользящего отра-

жения

При неравных нулю трансляциях

t преобразования {R/t}, оче-

видно, нелинейны. Тем не менее, они образуют группу, если под

произведением двух элементов понимать их повторное примене-

ние, определяемое выражением 1.97:

r′ = {R

}{R

} r = {R

}(R

r + t

) =

r + t

) + t

= R

r + R

+ t

откуда

{

}{R

} = R

+ R

+ t

. (1.99)

Единичным элементом пространственной группы является

{

E/O}, где E − тождественное преобразование пространства, O −

трансляция на нулевой вектор.

С помощью соотношения (1.98) легко получить, что элементом,

обратным {

R/t}, является преобразование вида

{R/t}

–1

= {R

–1

/ − R

–1

t}. (1.100)

Преобразования {

E/t}, отвечающие параллельному переносу

пространства на вектор решетки, образуют группу бесконечного

порядка, называемую

трансляционной. Очевидно, что трансляци-

онная группа является подгруппой пространственной группы. В

кристаллическом пространстве возможно существование 14 раз-

личных трансляционных групп, которые изоморфно отображаются

на четырнадцать уже описанных решеток Бравэ.

Преобразования, включающие трансляцию, являются открыты-

ми элементами симметрии. Любая точка преобразуется этими эле-

ментами в бесконечную совокупность точек.

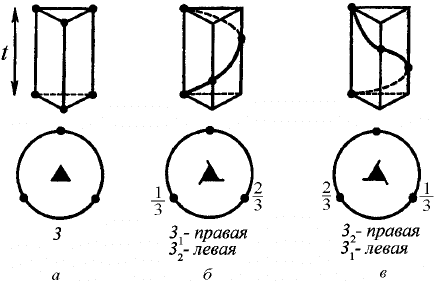
Винтовой осью симметрии называется совокупность оси сим-

метрии и параллельного ей переноса,

действующих совместно.

Различают правые и левые винтовые оси. В случае правой вин-

товой оси перемещение вдоль оси сопряжено с вращением по часо-

вой стрелке, а в случае левой − против часовой стрелки. Винтовая

ось обозначается двумя цифрами, например

. Большая цифра ука-

зывает порядок оси. Частное от деления цифры, стоящей в индексе

(1), на большую (3), т.е. 1/3, дает величину переноса

t/3 вдоль оси

трансляции, где

t − период трансляции вдоль этой оси (рис. 1.44).

Рис. 1.44. Действие поворотной оси 3 (а) и винтовых осей

симметрии

(б) и 3

(в)

Например, оси 2

соответствует поворот на угол α

= 180

смещение на 1/2 периода трансляции; эту ось можно считать как

право-, так и левовращающей.

Рассмотрим преобразование произвольной точки r(x,y) под дей-

ствием винтовой оси

вдоль оси a

, точка r переходит в r′:

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

′

2/1

100

010

001

а после повторной операции получим

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

′

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

′′

′

2/1

100

010

001

что соответствует трансляции вдоль

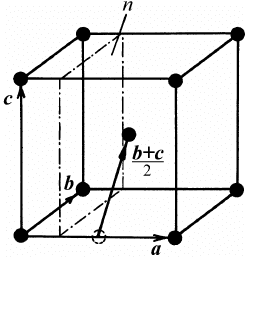
Плоскостью скользящего отраже-

ния

называется совокупность совмест-

но действующих

плоскости симметрии

и параллельной ей трансляции. Плос-

кость скользящего отражения

a (b, c)

типа соответствует отражению в плос-

кости и последующей трансляции на

t = a/2 (или b/2, c/2). Возможны и опе-

рации скользящего отражения

n-типа

(

клиноплоскости), когда трансляцион-

ная компонента расположена вдоль

диагонали грани

t = (a + b)/2, или t =

= (

a + c)/2, или t = (b + c)/2 (рис. 1.45).

Рис. 1.45. Плоскость

скользящего отражения

в ОЦК ячейке

Наконец, операции скользящего отражения с

t = (a ± b)/4, t =

= (

a ± c)/4, t = (b ± c)/4, t = (a ± b ± c)/4 соответствует алмазная

плоскость скольжения d

− типа.

Плоскость скользящего отражения, перпендикулярная

трансляцией в направлении

, соответствует преобразованию

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

′

2/12/1

100

010

001

а после повторной операции получим

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

′

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

′′

′

2/1

100

010

001

что соответствует трансляции в направлении

Исследование возможных комбинаций открытых и закрытых

элементов симметрии, проведенное одновременно и независимо

русским кристаллографом Е.С. Федоровым и А. Шенфлисом, при-

вело к установлению 230 пространственных групп симметрии.

В 73 симморфных пространственных группах точечные группы

являются подгруппами пространственных групп, в несимморфных

пространственных группах точечные группы не являются подгруп-

пами пространственных групп из-за наличия винтовых осей или

плоскостей скользящего отражения.

Правильной системой точек называется совокупность симмет-

рично эквивалентных позиций (точек), связанных между собой

симметричными преобразованиями пространственной группы.

Правильную систему точек можно получить из одной точки, по-

вторив ее при помощи всех операций, свойственных данной про-

странственной группы.

Понятие правильной системы точек для пространственной

группы играет такую же роль, как понятие простой формы для то-

чечной группы. Правильная система точек характеризует геомет-

рические законы пространственного расположения структурных

единиц в кристалле.

Как и для простой формы, для правильной системы точек суще-

ствуют понятия общей и частной систем.

Частная правильная сис-

тема точек

получается, если исходная точка лежит хотя бы на од-

ном из элементов симметрии или отстоит на равных расстояниях от

одинаковых элементов симметрии.

Общая правильная система то-

чек

получается, если исходная точка (а значит, и все остальные, ей

симметрично эквивалентные) не соприкасается ни с одним из эле-

ментов симметрии и лежит не на равных расстояниях от одинако-

вых элементов симметрии.

Кратностью правильной системы точек называется число точек

в элементарной ячейке, симметрично эквивалентных друг другу.

Кратность аналогична числу граней простой формы. У точек общей

правильной системы кратность выше, чем у частной.

В международном символе пространственной группы на первом

месте всегда стоит буква, обозначающая тип решетки, далее − по-

рождающие элементы симметрии, каждый на определенном месте.

Нарушение порядка записи меняет смысл символа.

В символе пространственной группы кубической сингонии на

первой позиции указан тип ячейки Бравэ, а на третьей позиции все-

гда стоит цифра

3, означающая четыре оси третьего порядка вдоль

направлений <111>. Буквы или цифры, стоящие на второй позиции

перед цифрой

3, определяют плоскости или оси, параллельные на-

правлениям <100>, а на четвертой − параллельные <110>.

В структуре алмаза вдоль <100>проходит плоскость

d, а в <110>

плоскости

n и m; выбирая из них более простые m, записываем

пространственную группу алмаза как

Fd3m. Пространственная

группа для меди −

Fm3m, а для вольфрама − Im3m.

Антисимметрия. А. В. Шубников ввел в учение о симметрии

новое понятие

антисимметрии. Преобразование антисимметрии

вводится для объектов, обладающих свойством изменения знака.

Как указал Шубников, такие физически реальные объекты, как

электрон и позитрон, фотографические негатив и позитив, требуют

введения в учение о симметрии понятия противоположно равных,

или антиравных, фигур. Антиравными считаются фигуры геомет-

рически равные, но имеющие разный знак.

С помощью представлений о черно-белой симметрии магнитные

свойства кристаллов хорошо описываются с помощью 90 магнит-

ных точечных групп.

Добавление элементов антисимметрии к обычным элементам

симметрии пространственных групп позволило вывести 1651 шуб-

никовскую группу.

Дальнейшим развитием учения о симметрии является теория

многоцветных (беловских) пространственных групп, названных так

по имени автора этой идеи Н.В. Белова.

Двухмерная кристаллография. В двухмерной кристаллогра-

фии возможны поворотные оси

1, 2, 3, 4, 6 порядков, четыре синго-

нии: косоугольная (

≠ а

, γ ≠ 90°), прямоугольная (а

≠ а

, γ = 90°),

гексагональная (а

= а

, γ = 120°) и квадратная (а

= а

, γ = 90°). В

каждой из сингоний существует примитивная ячейка

P и только в

прямоугольной − центрированная

C решетка Бравэ. Комбинации

поворотных и трансляционных элементов симметрии дают 17 про-

странственных групп.

Несоразмерные кристаллы и квазикристаллы. Наряду с

трехмерной (3

D) и двухмерной (2D) кристаллографией существует

четырехмерная (4

D) кристаллография. В 4D кристаллографии по-

являются запрещенные в 3

D кристаллографии оси симметрии 5, 8,

10 и 12 порядков, число решеток Бравэ возрастает до 64, точечных

групп − до 227, а число пространственных групп достигает 4895.

Прямая и обратная решетки кристаллов обладают трансляцион-

ной симметрией и симметрией точечных групп. В последние годы

рассматривают трансляционно-упорядоченные структуры, разде-

ляющиеся на периодические структуры (кристаллы) и квазиперио-

дические структуры в зависимости от того, являются ли их обрат-

ные решетки периодическими или квазипериодическими. В свою

очередь, квазипериодические структуры разделяют на

несоразмер-

ные кристаллы

и квазикристаллы. Несоразмерные кристаллы −

квазипериодические структуры с кристаллографической группой

симметрии, а квазикристаллы − квазипериодические структуры с

некристаллографической точечной группой. Примером квазикри-

сталлов могут быть покрытия Пенроуза с осью симметрии 5-го по-

рядка (двумерные квазикристаллы) или недавно открытые икосаэд-

рические сплавы алюминия с марганцем (икосаэдр − двацатигран-

ник с шестью осями 5-го порядка).

Экспериментальное определение элементов симметрии.

Атомное строение определяется по дифракции и рассеянию рент-

геновских лучей, электронов и нейтронов. Кристаллы с их трех-

мерными периодическими структурами являются естественными

дифракционными решетками для рентгеновских лучей, поскольку

длины волн рентгеновского излучения и межатомные расстояния в

кристаллах по порядку величины соизмеримы. Дифракционные

максимумы возникают во всех направлениях, отвечающих

уравне-

нию Вульфа

−Брэгга