Калин Б.А. Физическое материаловедение. Том 1. Физика твердого тела

Подождите немного. Документ загружается.

Ш(r) = , (1.54)

∑∑∑

−

+∞

−∞=

+∞

−∞=

+∞

−∞=mn p

mnp

)( Rr

Ш(h) = , (1.55)

∑∑∑

−

+∞

−∞=

+∞

−∞=

+∞

−∞=hkl

hkl

)( Hh

где r и h – текущие векторы в прямом и обратном пространствах

соответственно.

Функции Ш(r) и Ш(h) связаны взаимным преобразованием Фу-

рье, поэтому обратное пространство называют

фурье-пространст-

вом.

Так, при рассмотрении дифракции рентгеновских лучей на

кристаллах в прямом пространстве задается электронная плотность

ρ(r), а в обратном – амплитуда рассеянного рентгеновского излуче-

ния

A(h). По этой причине обратное пространство называют ди-

фракционным пространством.

1.2.5. Матрица ортогонального преобразования

Для описания поворотных элементов симметрии используются

матрицы ортогонального преобразования, которые сохраняют дли-

ны векторов и углы между ними. Для матрицы ортогонального

преобразования A выполняется соотношение

∑

δ=

klilik

(k, l = 1, 2, 3), (1.56)

где a

− элементы матрицы A, а δ

= 1 при k = l и δ

= 0 при k ≠ l.

Если A − матрица ортогонального преобразования, то detA = ±1 и

–1

= A

. Матрица A с detA = +1 соответствует собственному пово-

роту, а с detA = −1 − несобственному повороту.

В случае вещественной ортогональной матрицы собственные

значения встречаются комплексно-сопряженными парами, по мо-

дулю равными единице, а в матрицах нечетной размерности, по

крайней мере, одно собственное значение вещественно.

Таким образом, собственные значения матрицы A должны иметь

вид: 1, exp(−iα), exp(+iα). При этом фаза α комплексного собствен-

ного значения называется углом поворота, а собственный вектор u

с собственным значением λ = 1 называется осью поворота.

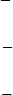
Угол поворота α находят из линейного инварианта матрицы по-

ворота A, т.е. из ее следа (обозначают trA от английского слова

«trace» или SpA − от немецкого «Spur»)

trA = a

+ a

= 1 + exp(−iα) + exp(+iα) = 1 + 2cosα. (1.57)

Компоненты оси поворота определяются из элементов матрицы

поворота A как

: u

= (a

− a

) : (a

− a

) : (a

− a

). (1.58)

Направляющие косинусы оси вращения u определяются как

133

122

111

)(

−

++=

uuuul

. (1.59)

В общем случае матрица поворота на угол φ вокруг оси

u с на-

правляющими косинусами l

, l

имеет вид

) ,(

uR =

⎟

⎠

⎞

⎜

⎝

⎛

ϕ+ϕ−ϕ+ϕ−ϕ−ϕ−

ϕ−ϕ−ϕ+ϕ−ϕ+ϕ−

ϕ+ϕ−ϕ−φ−ϕ+ϕ−

cos)cos1(sin)cos(1sin)cos(1

sin)cos(1cos)cos1(sin)cos(1

sin)cos1(cos)cos1(cos)cos1(

3132231

132

2321

231321

lllllll

.(1.60)

Если поворот задан эйлеровскими углами φ, θ, ψ, то каждая из

матриц поворота имеет простой вид в соответствующей поверну-

той системе координат (рис. 1.24). Так матрицы первого поворота

на угол φ вокруг оси z −

(φ), второго поворота на угол θ вокруг

оси x′ −

x′

(θ) и третьего поворота на угол ψ вокруг оси z′ − R

z′

(ψ)

имеют вид:

(φ) = , R

x′

(θ) = ,

⎟

⎠

⎞

⎜

⎝

⎛

ϕϕ

ϕ−ϕ

100

0cossin

0sincos

⎟

⎠

⎞

⎜

⎝

⎛

θθ

θ−θ

cossin0

sincos0

001

z′

(ψ) = .

⎟

⎠

⎞

⎜

⎝

⎛

ψψ

ψ−ψ

100

0cossin

0sincos

Матрица поворота

R(φ, θ, ψ) обычно записывается в неподвиж-

ной системе координат xyz, причем если ее выражать через матри-

цы R

(φ), R

X′

(θ) и R

Z′

(ψ), то порядок их перемножения обратен по-

рядку выполняемых поворотов, т.е.

R(φ, θ, ψ) = R

(φ) R

X′

(θ) R

Z′

(ψ),

так что

),,(

R =

.(1.61)

⎟

⎠

⎞

⎜

⎝

⎛

θψθψθ

ϕθ−ψϕθ+ψϕ−ψϕθ+ψϕ

ϕθψϕθ−ψϕ−ψϕ−ψϕ

coscossinsinsin

cossincoscoscossinsinsincoscoscossin

sinsincossincossincossinsincoscos

Углы φ и ψ изменяются от 0 до 2π, а угол θ − от 0 до π.

Эйлеровские углы поворота часто используются в физике твер-

дого тела, в кристаллографии интересуются кристаллографически-

ми индексами оси поворота и значением угла поворота.

В результате поворота, определяемого матрицей

A, произволь-

ный вектор

r переходит в r′, что в матричном виде записывается

как

r′ = Ar, (1.62)

т.е.

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

′

333231

232221

131211

aaa

, (1.63)

где a

− элементы матрицы A, (r

, r

) − компоненты вектора r,

(r′

, r′

) − компоненты вектора r′.

Вообще говоря, матрица

A, как и любая матрица ортогонального

преобразования, допускает двойную интерпретацию: «активную» и

«пассивную». В первом случае матрица

A поворачивает вектор r на

угол α вокруг оси

u, переводя его в r′, причем оба вектора задаются

в одной системе координат. Во втором случае − при пассивной ин-

терпретации − можно считать, что матрица

A поворачивает систе-

му координат вокруг оси

u на угол α в противоположном направ-

лении, причем компоненты вектора

r не изменяются (рис. 1.36).

Компоненты матрицы

A легко определить, исходя из соотно-

шения (1.63). Действительно, направление [100] с координатами

, r

) после поворота имеет координаты (r′

, r′

). Таким об-

разом, матрицу

A можно представить состоящей из матриц-

столбцов

, a

, компонентами которых являются координаты

векторов [100], [010], [001] после поворота.

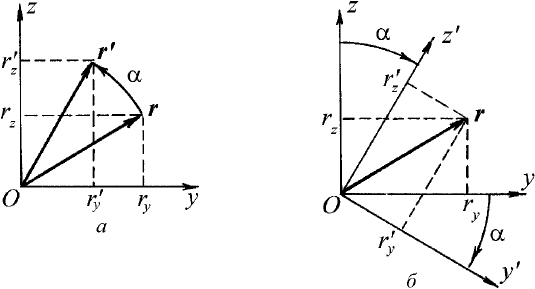
Рис. 1.36. Активная (а) и пассивная (б)

интерпретация поворота на угол α во-

круг оси x

Если матрица

A задает операцию в системе координат xyz

= Ar

, (1.64)

то в системе координат x'y'z' эта операция задается матрицей

= A'r'

Переход из системы координат xyz в систему координат x'y'z' осу-

ществляется матрицей

C, т.е.

= Cr

и r'

= Cr

, r

= C

–1

и r

= C

–1

Подставляя

и r

в (1.55), получим C

–1

= AC

–1

или, умножая

слева и справа на

C, имеем r'

= CAC

–1

. Матрица CAC

–1

= A'

осуществляет в системе координат x'y'z' такую же операцию, как и

A в системе xyz. Матрицы A и A', связанные соотношением

A' = CAC

–1

(1.65)

или, если

D = C

–1

, A' = D

–1

AD, называют матрицами подобия. У

матриц подобия равны все инварианты, в том числе и линейный

инвариант (след матрицы), т.е.

A = trA' = 1 + 2 cosα. (1.66)

1.2.6. Преобразование индексов направлений

и плоскостей при изменении системы координат

Произвольное направление [mnp] задается вектором

mnp

= ma

+ n

+ pa

или вектором = m

+ m

. В матричном

виде →

321

ттт

321

ттт

()

, (1.67) maaaa

321

⎟

⎠

⎞

⎜

⎝

⎛

где − матрица-строка из базисных векторов, а

m − матрица-

столбец из компонентов вектора.

При переходе из системы координат xyz к системе x'y'z' базисные

векторы преобразуются как

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

′

333332331

223222221

113112111

aAaAaA

, т.е. a' = Aa

или

Aaa

′

. (1.68)

Вектор

в новой системе координат переходит в R

′

= R

и с учетом (1.68)

mamAa

′

, (1.69)

откуда

m и =

′

−

m. (1.70)

Таким образом, при изменении системы координат базисные

векторы преобразуются как ковариантные векторы с помощью

матрицы

(1.68), а компоненты вектора R преобразуются как

контравариантные векторы с помощью матрицы

−

A . Иногда

матрицу

−

A называют матрицей контраградиентного

преобразования.

Скалярное произведение между векторами и

hkl

равно

hkl

= m

h + m

k + m

l или в матричной записи

321

ттт

321

ттт

()

⎟

⎠

⎞

⎜

⎝

⎛

lkh

= .

При изменении системы координат скалярное произведение сохра-

няется = и с учетом (1.70) =

′′

′

−

Am и =

′

−

A ,

откуда

′

. (1.71)

Следовательно, при изменении системы координат компоненты

вектора обратной решетки и базисные векторы преобразуются, как

ковариантные векторы с помощью матрицы

1.2.7. Основные формулы структурной

кристаллографии

Период идентичности. Период идентичности I

[mnp]

вдоль данно-

го направления [mnp] – расстояние между ближайшими узлами

вдоль данной прямой – равен абсолютной величине вектора

mnp

Длину вектора проще вычислить через скалярное произведение

[mnp]

= (R

mnp

)

1/2

, записанное в матричном виде.

Переходя от

mnp

к и учитывая соотношения (1.67) и

(1.71), запишем в прямом и обратном базисах как

321

ттт

321

ттт

321

ттт

R =

()

= (1.72) maaaa

321

⎟

⎠

⎞

⎜

⎝

⎛

()

hbbbb

321

⎟

⎠

⎞

⎜

⎝

⎛

и = . Умножая слева левую и правую часть последнего соот-

ношения на

a, получим = и, поскольку =G, =I, то

maa

hba

Gm = h. (1.73)

Аналогично, умножая на

b соотношение = , получим ma

m = . (1.74)

1−

Соотношение (1.73) показывает, что использование метрической

матрицы

G позволяет при известных компонентах m вектора

в прямом пространстве найти его компоненты

h в обратном

пространстве. Матрица

–1

аналогично переводит компоненты из

обратного пространства в прямое пространство. (1.74).

321

mmm

Теперь выражение для периода идентичности имеет вид

Gmm

321

mmm

I . (1.75)

Квадратичная форма. Длина вектора обратной решетки

hkl

H может быть представлена аналогично как

hkl

H = hGh

−

. (1.76)

Выражение

hkl

H= = , которое является функцией па-

раметров решетки a, b, c, α, β, γ, называют квадратичной формой

соответствующей сингонии.

hGh

−

Квадратичные формы для некоторых сингоний имеют вид:

для кубической сингонии

222

lkh

hkl

, (1.77)

для ромбической сингонии

hkl

++= , (1.78)

для гексагональной сингонии

(

)

khkh

hkl

= . (1.79)

Угол между направлениями. Угол φ между направлениями

() () ()

[

]

m m m и

(

)

(

)

(

)

[

]

m m m определяют из соотношения

cosφ =

(

)()

() ()

2211

GmmGmm

Gmm

, (1.80)

где

()

m ,

()

m − матрицы-строки;

(

)

m ,

(

)

m − матрицы-столбцы.

Угол между плоскостями. Угол φ между плоскостями

() () ()

(

)

h h h и

(

)

(

)

(

)

(

)

h h h равен углу между нормалями к этим

плоскостям:

cosφ =

(

)

(

)

() ()

212111

112

hGhhGh

hGh

−−

−

. (1.81)

Угол между плоскостью и направлением. Угол между плос-

костью и направлением

(

321

h h h

)

[

]

321

m m m

определяют через

угол φ между этим направлением и нормалью к плоскости:

cosφ =

GmmhGh

1−

. (1.82)

Объем элементарной ячейки. Объем элементарной ячейки, по-

строенной на базисных векторах прямой решетки a

, a

, выража-

ется смешанным произведением

V = a

×a

], (1.83)

или с использованием метрической матрицы прямой решетки

V = Gdet . (1.84)

Для обратной решетки, построенной на базисных векторах b

, b

, объем элементарной ячейки определяется аналогичными вы-

ражениями

V* = b

×b

] =

det

−

. (1.85)

1.2.8. Области Вороного, ячейки Вигнера−Зейтца,

зоны Бриллюэна

Можно дать другой способ выбора элементарной ячейки. Со-

единим нулевой узел пространственной решетки с ближайшими

узлами при помощи прямых и проведем через середины этих пря-

мых плоскости, к ним перпендикулярные. Получим ячейку, при

помощи параллельного переноса которой заполняется все про-

странство.

Эта ячейка примитивная, так как содержит всего один узел. Об-

ласть, определенная таким образом, называется в кристаллографии

областью Вороного, а в физике твердого тела ячейкой Вигнера–

Зейтца

В ГЦК решетке ближайшие узлы расположены вдоль направле-

ний <110>, поэтому ячейка Вигнера–Зейтца огранена плоскостями

{110}. Поскольку множитель повторяемости для {110} равен 12, то

ячейка Вигнера–Зейтца для ГЦК решетки образована двенадцатью

гранями {110}, имеющими форму ромба. Таким образом, ячейка

Вигнера–Зейтца для ГЦК решетки является правильным ромбиче-

ским додекаэдром (рис. 1.37,

а).

В случае ОЦК решетки ячейка Вигнера

−Зейтца огранена плос-

костями {111} (правильные шестиугольники) и {100} (квадраты).

Множители повторяемости для {111} и {100} равны соответствен-

но 8 и 6, и ячейка Вигнера

−Зейтца изображается многогранником с

14 гранями (рис. 1.37,

б).

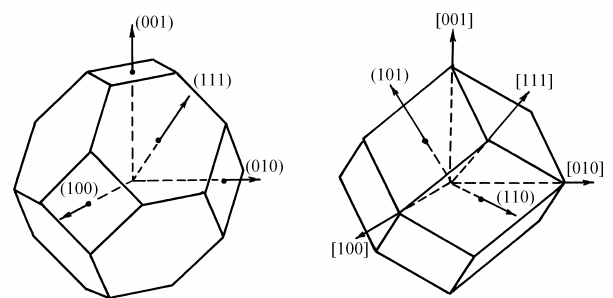
а б

Рис. 1.37. Ячейки Вигнера–Зейтца для ГЦК (а) и ОЦК кристаллов (б)

В физике твердого тела фундаментальное значение имеет ячейка

Вигнера

−Зейтца, построенная для обратной решетки. Эта ячейка

называется

зоной Бриллюэна. Как известно, ГЦК и ОЦК решетки

являются взаимно обратными и, следовательно, зона Бриллюэна

для ГЦК решетки изображается многогранником с 14 гранями, а

зона Бриллюэна для ОЦК решетки − правильным ромбическим до-

декаэдром.

1.3. Симметрия кристаллов

Симметрия кристаллического пространства определяется зада-

нием всех преобразований, которые сохраняют расстояния между

любыми точками пространства и приводят к совмещению про-

странства с самим собой. Элементы симметрии делят на закрытые

и открытые.

Открытые элементы симметрии содержат трансля-

ции и поэтому описывают симметрию бесконечного пространства.

Закрытые элементы симметрии оставляют одну точку неподвиж-

ной и после конечного числа операций возвращают кристалличе-

ское пространство в исходное положение. Закрытые элементы

симметрии задаются матрицами ортогонального преобразования R

с detR = ± 1. Они могут быть сведены к поворотным осям симмет-

рии (

чистое или собственное вращение с detR = + 1) и к инверси-

онным осям (вращение с отражением в точке, лежащей на оси,

или

несобственное вращение с detR = − 1).

1.3.1. Поворотные оси симметрии

Осью симметрии называют прямую, при повороте вокруг кото-

рой на некоторый угол α

гомологические (эквивалентные) точки

кристаллического пространства совмещаются. Угол поворота α

равен 360

/n, где n − целое число. Значит, через n поворотов в од-

ном направлении на угол α

кристаллическое пространство возвра-

щается в исходное положение. Наименьший угол поворота α

для

данной оси симметрии называют

элементарным углом оси симмет-

рии, а

n − порядком оси поворота. В кристаллографической системе

координат при повороте вокруг оси симметрии произвольный век-

тор x, задающий узел пространственной решетки, переходит в век-

тор x′:

x′ = Rx,

где R − матрица вращения, а x и x′ − векторы-столбцы.

Координатами векторов x и x′, определяющих узлы пространст-

венной решетки в кристаллографической системе координат, явля-

ются целые числа, поэтому компонентами матрицы R и, следова-

тельно, ее следа trR также являются целочисленные величины, т.е.

trR =

N, где N − целое число.

В ортогональной системе координат преобразование R будет

описываться матрицей подобия R

′ = CRC

-1

, где C − матрица пере-

хода от кристаллографической системы координат к ортогональной

системе. Если ортогональную систему координат выбрать таким

образом, чтобы ось симметрии совпала с осью

x, то поворот вокруг

этой оси будет описываться матрицей R

′ вида

′ =

(1.86)

⎟

⎠

⎞

⎜

⎝

⎛

αα

α−α

cossin0

sincos0

001

След этой матрицы tr

R′ = trR = N = 1 + 2 cosα; N может прини-

мать значения 0, ±1, +2, +3. Отсюда следует, что возможны лишь

повороты на угол α,

равный 0, 60, 90, 120 и 180° (табл. 1.2). Таким