Калин Б.А. Физическое материаловедение. Том 1. Физика твердого тела
Подождите немного. Документ загружается.

Две частичные дислокации, связанные между собой полосой
дефекта упаковки, называют
растянутой дислокацией.
На рис. 2.81 показана схема строения кристалла с двумя экстра-
плоскостями, вокруг края которых проходит единичная дислока-
ция. Энергия такой полной дислокации может сильно понизиться,
если две полуплоскости будут удалены одна от другой.
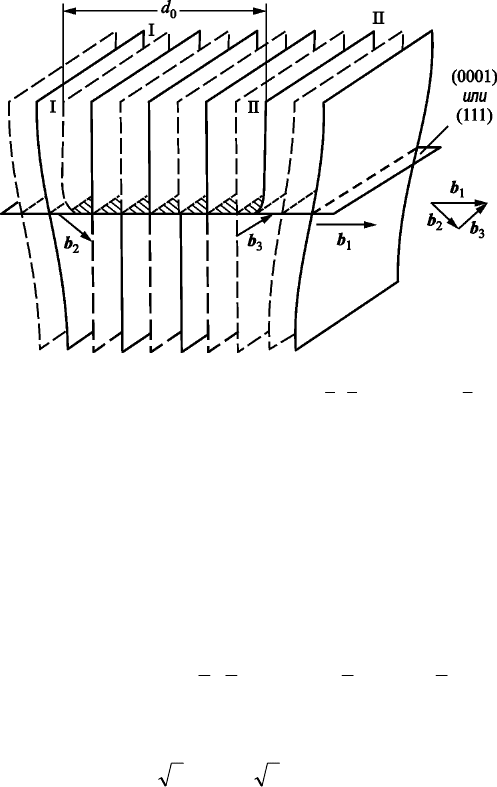
Рис. 2.81. Растянутая краевая дислокация в ГПУ и ГЦК структурах:
d
0
– ширина дефекта упаковки; b
1
= 1/3
[
]
0121 или а/2
[
]
101
Вокруг края каждой из этих экстраплоскостей проходит частич-
ная дислокация Шокли, а в плоскости сдвига между краями экст-
раплоскостей находится полоса дефекта упаковки. В действитель-
ности частичные дислокации здесь не чисто краевые, так как век-
торы Бюргерса
b
1
и b
2
не перпендикулярны их линиям.
Поскольку единичная дислокация, стремясь уменьшить энер-
гию, расщепляется на две частичные дислокации, соединенные де-
фектом упаковки, то растянутую дислокацию называют также
рас-
щепленной
. Реакция диссоциации единичной дислокации в ГПУ
структуре выглядит так: 1/3
[
]
0121 = 1/3
[
]
0101 + 1/3
[
]
1001.
Проверка по критерию Франка показывает, что такая реакция
диссоциации возможна:
а
2
> (а/ 3)
2
+ (а/ 3)
2
или а
2
> 2а
2
/3.
291

Критерий Франка учитывает только сумму упругих энергий
двух образовавшихся при расщеплении дислокаций и не учитывает
энергию дефекта упаковки. Энергия растянутой дислокации равна
сумме энергий двух частичных дислокаций, энергии их упругого
отталкивания и энергии дефекта упаковки.
Так как дефект упаковки повышает энергию кристалла, то де-
фект упаковки стремиться уменьшить свою площадь. Энергия,
приходящаяся на единицу площади дефекта упаковки, является
поверхностной энергией, ее размерность Дж/м
2
= Нм/м
2
= Н/м.
Растянутая дислокация способна скользить в плоскости дефекта
упаковки: головная частичная дислокация, передвигаясь, оставляет
за собой дефект упаковки; скользящая за ней замыкающая (хвосто-
вая) дислокация ликвидирует дефект упаковки. Вся растянутая
дислокация перемещается как единое целое. Результат перемеще-
ния растянутой дислокации в точности такой же, как получился бы
при скольжении единичной дислокации. Обусловлено это тем, что
соблюдается векторная сумма
b
1
= b
2
+ b
3
.
Аналогичным образом образуются частичные дислокации Шок-
ли и в ГЦК структуре, только там дефект упаковки лежит в плот-
ноупакованных плоскостях
{111}. Реакцию расщепления единич-
ной дислокации в ГЦК структуре можно представит следующим
образом (рис. 2.82):
а/2 ]101[ = а/6 ]121[ + а/6 ]211[.
Рис. 2.82. Векторы Бюргерса единичных дислокаций (b
1
, b
5
) и частичных
дислокаций Шокли (
b
2
, b
3
, b
4
) в ГЦК структуре:
а – элементарная ячейка; б – плоскость )111( ; b
1
= а/2
[
]
101 , b
2
= а/6
[
]
121,
b
3
= а/6
[
]
211 , b
4
= а/6
[
]
112, b
5
= а/2
[
]
101
292

Проверка по критерию Франка показывает, что такая реакция
диссоциации возможна:
(
а 2 /2)
2
> (а
6
/6)
2
+ (а
6
/6)
2
или
а
2
/2 > а
2
/3.
В ГЦК структуре дефект представляет тонкую прослойку с че-
редованием плотноупакованных слоев
САСАСА…, характерным
для ГПУ структуры. Растянутая дислокация в ГЦК структуре
скользит по направлению плотнейшей упаковки
011 таким же
образом как и в ГПУ структуре: головная частичная дислокация
Шокли создает дефект упаковки, а хвостовая устраняет.
В качестве примера расщепления единичной дислокации в ОЦК
структуре на две частичных дислокаций Шокли можно привести
следующую реакцию:
а/2
[
]
111 = а/6
[
]
111 + а/3
[
]
111.
Согласно критерию Франка, эта реакция энергетически выгодна,
так как
2
2
3
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
а
=
2
6
3
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
а
+
2
3
3
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
а
или
4
3
2
а
>
12
5
2
а
.
Практически такое расщепление будет иметь место, если энер-
гия образующегося дефекта упаковки мала.
Частичные дислокации Франка. Частичные дислокации Шок-
ли создавались несквозным сдвигом в плоскости плотнейшей упа-
ковки, когда возникающий дефект упаковки оканчивался внутри
кристалла. Его границей внутри кристалла и была частичная дис-
локация Шокли. Дефект упаковки, как указывалось выше, можно
получить и другим путем. Если в ГЦК структуре удалить часть
плотноупакованного слоя и ликвидировать образовавшуюся
«щель», сблизив по нормали соседние плотноупакованные слои, то
возникнет дефект упаковки вычитания. Граница его внутри кри-
сталла – линейное несовершенство, называемое частичной дисло-
кацией Франка (рис. 2.83).
293

Рис. 2.83. Дислокация Франка в ГЦК структуре. Линия дислокации лежит
в плоскости
{111}, перпендикулярной плоскости чертежа {110},
и выходит на плоскость чертежа в точке
а:
1 – атомы в плоскости рисунка; 2 – атомы непосредственно над ней
В данном случае дислокация Франка расположена перпендику-
лярно площади чертежа, и видно только ее выход на эту плоскость.
Область несовершенства тянется вдоль края неполной атомной
плоскости. Сближение атомов, которое необходимо для ликвида-
ции «щели», происходило на величину вектора а/3
111 , т.е. на
а
3/3 по нормали к плоскости плотнейшей упаковки. Следова-
тельно, вектор Бюргерса дислокации Франка перпендикулярен ли-
нии дислокации, т.е. дислокация Франка – краевая.
При внедрении между слоями {111} неполного плотноупако-
ванного атомного слоя возникает дефект упаковки внедрения (рис.
2.84), границей которого также является частичная дислокация
Франка с вектором Бюргерса а/3
111 , перпендикулярным линии
дислокации (атомы соседних слоев удаляются по нормали от плос-
кости {111}.
Так как вектор Бюргерса дислокации Франка не лежит в плоско-
сти дефекта упаковки, то эта дислокация не может двигаться
294
скольжением подобно тому, как легко скользит единичная краевая
дислокация. Дислокация Франка может перемещаться только пере-
ползанием в плоскости дефекта упаковки при достройке неполного
атомного слоя или при удалении атомов с его кромки. Поэтому
частичные дислокации Франка называются также сидячими или
полузакрепленными. В отличие от них частичные дислокации
Шокли и все полные дислокации называются скользящими.
Рис. 2.84. Двойная дислокационная петля Франка в ГЦК структуре
Плоскую петлю, внутри которой заключен дефект упаковки, на-
зывают сидячей дислокационной петлей Франка. Ее вектор Бюр-
герса перпендикулярен плоскости петли.
В ГПУ структуре частичные дислокации Франка являются гра-
ницами дефектов упаковки, которые можно получить при внедре-
нии или удалении неполного плотноупакованного слоя {0001}. На-
пример, при внедрении в чередование слоев АВАВАВ… между
слоями А и В диска из атомов в положениях С возникает дефект
упаковки, границей которого является частичная дислокация
Франка с вектором Бюргерса 1/2
0001 , перпендикулярным плос-
кости базиса. Величина вектора Бюргерса этой дислокации равна
с/2 или для случая идеального отношения с/а =
3
8
= 1,633.
295
В ОЦК структуре сидячая частичная дислокация с чисто крае-
вой ориентацией является границей дефекта упаковки, полученно-
го внедрением двух неполных слоев в семейство параллельных
слоев {112}. Ее вектор Бюргерса а/3
112 перпендикулярен плос-
кости {112}.
2.2.7. Дислокационные реакции
Стандартный тетраэдр и дислокационные реакции в ГЦК
структуре.
Векторы Бюргерса в ГЦК структуре принято рассмат-
ривать, используя специальный геометрический образ – стандарт-
ный тетраэдр Томпсона (рис. 2.85).
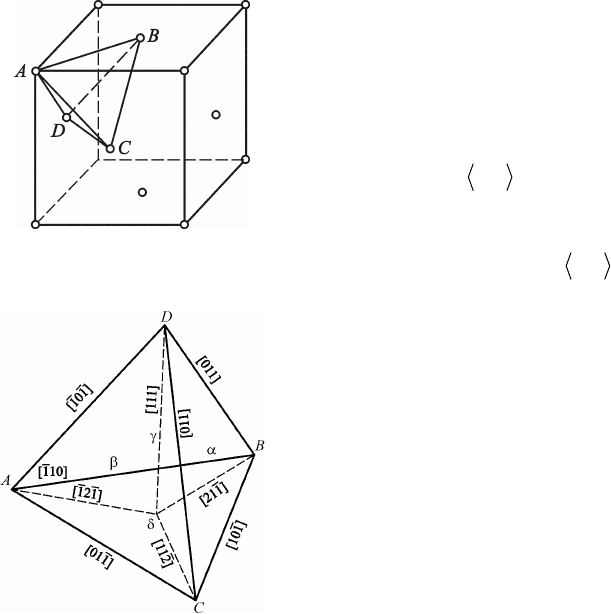
Рис. 2.85. Стандартный тетраэдр
Томпсона
Рис. 2.86. Расположение
стандартного тетраэдра Томпсона
в элементарной ячейке ГЦК
решетки
Стандартный тетраэдр состоит из
четырех равносторонних треугольни-
ков – плоскостей {111}. Его вершины
совпадают с узлами ГЦК решетки, в
которых находятся четыре соседних
атома (рис. 2.86). Ребра тетраэдра рас-
положены вдоль кристаллографиче-
ских направлений
110 . Ребра АВ,
ВС, АС, АD, ВD и СD представляют
собой всевозможные векторы Бюргер-
са единичных дислокаций а/2
110 в
ГЦК решетке, а боковые грани – все
плоскости скольжения {111}.
Буквами α, β, γ и δ на рис. 2.86
обозначены точки центра тяжести
треугольных граней, противополож-
ных вершинам А, В, С и D, соответст-
венно. Лежащие в плоскостях {111}
отрезки типа Аδ, δC, Bα и Dα пред-
ставляют собой все возможные век-
торы Бюргерса а/6〈112〉 частичных
дислокаций Шокли. Отрезки типа Dδ,
соединяющие вершину и центр тяже-
сти противолежащей грани, представ-
ляют собой все возможные векторы
Бюргерса а/3〈111〉 частичных дисло-
каций Франка.
296
Для перехода от обозначений Томпсона к кристаллографиче-
ским индексам и обратно удобно пользоваться разверткой тетраэд-
ра Томпсона (рис. 2.87).
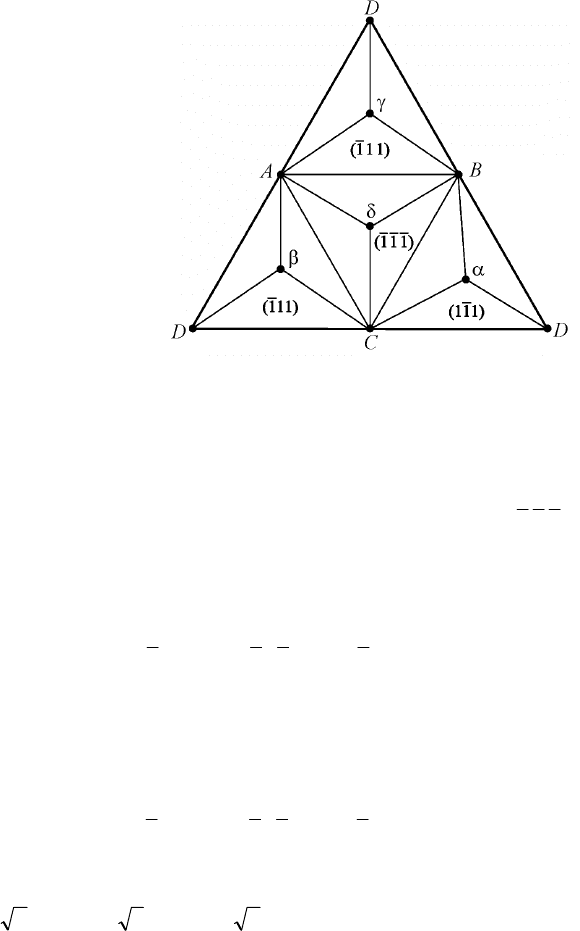
Рис. 2.87. Развертка
тетраэдра Томпсона
С помощью стандартного тетраэдра легко записывать дислока-
ционные реакции в ГЦК решетке. Например, расщепление единич-
ной дислокации на две частичные дислокации Шокли в обозначе-
ниях Томпсона можно записать так:
АС = Аδ +δС.
Эта реакция происходит в плоскости АВС с индексами (
111
).
В этой же плоскости возможна реакция расщепления дислокации
АВ на две частичные дислокации Шокли Аδ и δВ: АВ = Аδ + δВ. В
кристаллографических индексах эта реакция записывается сле-
дующим образом:
а/2
[
]
101 = а/6
[
]
121 + а/6
[
]
112.
Аналогично записываются и другие возможные дислокацион-
ные реакции. Например, расщепление единичной дислокации АВ
на частичную дислокацию Франка Аα и частичную дислокацию
Шокли αВ в обозначениях Томпсона запишется, как АВ = Аα+αВ, а
в кристаллографических индексах
а/2
[
]
101 = а/3
[
]
111 + а/6
[
]
121.
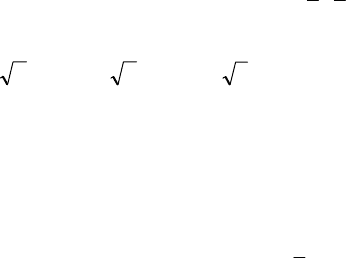
Используя критерий Франка (правило квадратов), нельзя сде-
лать определенное заключение о направлении данной реакции, так
как (а
2
/2)
2
= (а 3/3)
2
+ (а 6/6)
2
. Однако, учитывая, что при
расщеплении единичной дислокации образуется дефект упаковки,
297
следует считать, что энергетически выгодной будет не реакция
расщепления, а реакция объединения частичной дислокации Фран-
ка и частичной дислокации Шокли в единичную дислокацию с уст-
ранением дефекта упаковки.
Здесь уместно подчеркнуть, что отрезки АВ, Аα и αВ являются
векторами Бюргерса дислокаций, а не их линиями. Линия дислока-
ции Франка с вектором Бюргерса Аα и связанный с ней дефект
упаковки лежит в плоскости DВС. В этой же плоскости лежит ли-
ния дислокации Шокли с вектором Бюргерса αВ и связанный с ней
дефект упаковки.
Реакция DА + Аδ = Dδ описывает объединение единичной дис-
локации и дислокации Шокли из разных плоскостей скольжения в
дислокацию Франка. Дислокация с вектором Бюргерса DА может
скользить в плоскости АDВ или АDС. Линия дислокации Шокли с
вектором Бюргерса Аδ и связанный с ней дефект упаковки нахо-
дится в плоскости АВС. Образующаяся дислокация Франка также
находится в плоскости АВС. В обычных кристаллографических
символах реакция имеет вид: а/2
[
]
101
+ а/6
[
]
121 = а/3
[
]
111
.
Из критерия Франка вытекает, что такая реакция вдвое снижает
энергию (а
2
/2)
2
+ (а 6/6)
2
> (а 3/3)
2
. Если дислокация Шокли
является частью растянутой дислокации Шокли – Шокли, то объе-
динение ее с единичной дислокацией по указанной реакции дает
растянутую дислокацию Шокли – Франка.
Используя стандартный тетраэдр (см. рис. 2.85), рассмотрим
встречу двух растянутых дислокаций, движущихся в пересекаю-
щихся плоскостях скольжения.
Допустим, что в плоскости АDС, т.е. (
111 ), находится расщеп-
ленная дислокация АD, состоящая из частичных дислокаций Шок-
ли Dβ и βА, соединенных дефектом упаковки. В плоскости АВС,
т.е. (111), находится расщепленная дислокация АС, состоящая из
частичных дислокаций Аδ и δС и дефекта упаковки (рис. 2.88)
В то время как в стандартном тетраэдре отрезки Dβ, βA, Aδ и δС
изображают векторы Бюргерса дислокаций Шокли, то на рис. 2.87
обозначенные этими же символами отрезки изображают сами ли-
нии дислокаций.
298

Рис. 2.88. Образование дислокации Ломер – Коттрелла при встрече
растянутых дислокаций в пересекающихся плоскостях скольжения:
а – до встречи, б – после встречи
Плоскости АDС и АВС пересекаются по прямой с индексами
[
]
101 . При движении растянутых дислокаций их головные частич-
ные дислокации βA и Aδ могут встретиться на линии пересечения
плоскостей скольжения и образовать в месте встречи новую час-
тичную дислокацию. Вектор Бюргерса этой дислокации легко оп-
ределить в тетраэдре (см. рис. 2.85): βA + Aδ = βδ. Отрезок βδ, со-
единяющий центры двух граней, параллелен ребру DВ с индексами
[011]. Можно показать, что отрезок βδ равен одной трети отрезка
DВ и, следовательно, вектор Бюргерса дислокации встречи запи-
шется как а/6[011]. Объединение двух головных частичных дисло-
каций в одну частичную по реакции а/6
[
]
211 + а/6
[
]
121 = а/6[011]
дает большой выигрыш в энергии, так как (а
6/6)
2
+ (а 6/6)
2
>
(а
2/6)
2
.
Дислокация с вектором Бюргерса а/6[011] также частичная. Ее
линия идет вдоль направления
[
]
101 и находится в вершине дву-
гранного угла, образованного встретившимися дефектами упаковки
из пересекающихся плоскостей скольжения. Поэтому дислокации
типа а/6
110 называют вершинными.
Легко видеть, что линия вершинной дислокации, которая на-
правлена по
[
]
101 , и вектор Бюргерса вершинной дислокации
299
а/6[011] взаимно перпендикулярны. Это говорит о том, что вер-
шинная дислокация чисто краевая. В результате встречи в пересе-
кающихся плоскостях двух растянутых дислокаций образуется но-
вая растянутая дислокация, в которой дефект упаковки имеет фор-
му клина (см. рис. 2.88) в вершине которого находится вершинная
дислокация βδ, а по краям частичные дислокации Шокли Dβ и δС.
Такую совокупность трех частичных дислокаций и клинообразного
дефекта упаковки называют дислокацией Ломер–Коттрелла.
Основные сведения обо всех рассмотренных характерных дис-
локациях в ГЦК решетке приведены в табл. 2.7.
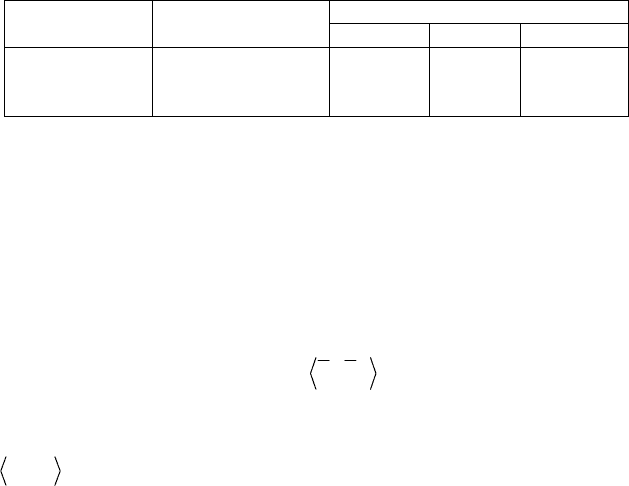
Таблица 2.7
Характерные дислокации в ГЦК структуре
Частичные Тип Полные
Шокли Франка Вершинные
Вектор Бюргерса
Квадрат вектора
Бюргерса
а/2<110> а<110>
а
2
/2 а
2
а/6 <112>
а
2
/6
а/3<111>
а
2
/3
а/6<110>
а
2
/18
Стандартная пирамида и дислокационные реакции в ГПУ
структуре.
Для упрощения анализа поведения дислокаций в ГП
решетке используют построение, называемое стандартной бипира-
мидой, представленной на рис. 2.89
Для ГПУ структуры характерны три вида полных и три вида
частичных дислокаций.
1. Полные дислокации с векторами Бюргерса АВ, ВС и АС. Со-
кращенно их называют а-дислокациями. Вектор Бюргерса в кри-
сталлографических символах 1/3
0121.
2. Полные дислокации с вектором Бюргерса ST, перпендикуляр-
ным базисной плоскости. Их называют с-дислокациями или
0001
-дислокациями.
3. Полные дислокации с векторами Бюргерса типа AD, находя-
щимися в призматических плоскостях. Отрезок AD (вне пирамиды)
является вектором тождественной трансляции решетки, так как уз-
300
