Калин Б.А. Физическое материаловедение. Том 1. Физика твердого тела

Подождите немного. Документ загружается.

Энергия связи с дислокацией атомов внедрения значительно

выше, чем атомов замещения, и поэтому при одинаковой общей

концентрации C

в растворах внедрения Т

выше, чем в растворах

замещения. Иными словами, в растворах замещения при нагрева-

нии атмосфера Коттрела перестает быть насыщенной при более

низкой температуре.

Чем больше плотность дислокации, тем больше требуется ато-

мов примеси, чтобы образовать насыщенные атмосферы. Концен-

трация примесных атомов, расположенных в виде непрерывных

одноатомных цепочек вдоль линий дислокаций, C = ρа

; где ρ –

плотность дислокаций, а – межатомное расстояние. Если в ото-

жженном металле плотность дислокаций порядка 10

см

–2

, а в на-

клепанном 10

см

–2

, то С ~ 10

–6

и 10

–3

ат. %. Следовательно, и в

сильно наклепанном металле технической чистоты количество

атомов примесей достаточно, чтобы они могли создать насыщен-

ные атмосферы на всех дислокациях при температурах ниже Т

Например, в железе примеси углерода и азота, растворенные по

способу внедрения (Е

max

= 0,5 эВ), при комнатной температуре об-

разуют насыщенные атмосферы.

Низкие значения Е

max

в растворах замещения с ГЦК решеткой

могут компенсироваться высокой общей концентрацией раствора

, и в этом случае температура Т

также может оказаться доволь-

но высокой. Например, α-латунь содержит 1 aт.% Zn; при Е

max

= 0,1

эВ – Т

= 300 K, т.е. при

комнатной температуре атмо-

сферы вокруг дислокации насы-

щены атомами Zn

Очевидно, что наличие лю-

бых атмосфер будет тормозить

движение дислокаций. Величина

напряжения, необходимого для

отрыва дислокаций от атмосфе-

ры Коттрела, будет зависеть от

насыщенности атмосферы. Рас-

смотрим отрыв краевой дисло-

кации от блокирующих ее ато-

мов примеси (рис. 2.50).

Рис. 2.50. К определению напряжения,

необходимого для отрыва дислокации

от атмосферы Коттрела

251

Как было показано выше, энергия взаимодействия дислокации и

атомов примеси описывается выражением Е

вз

= B

θsin

. Отсюда ра-

боту, которую необходимо затратить для перемещения дислокации

в плоскости скольжения на расстояние x от атомов примеси, можно

определить как А =

, так как sinθ =

, r =

rx + .

Тогда сила, приходящаяся на одну атомную плоскость, пересе-

каемую дислокацией, необходимая для того, чтобы передвинуть

дислокацию на расстояние x , равна

= –

∂

)(

xBr

Если продифференцировать это выражение и приравнять его

нулю, то можно найти расстояние дислокаций до ряда примесных

атомов в случае максимальной величины силы F

. При этом полу-

чим, что х =

а соответствующая величина силы, приходя-

щейся на одну атомную плоскость, будет

max

= (2.62)

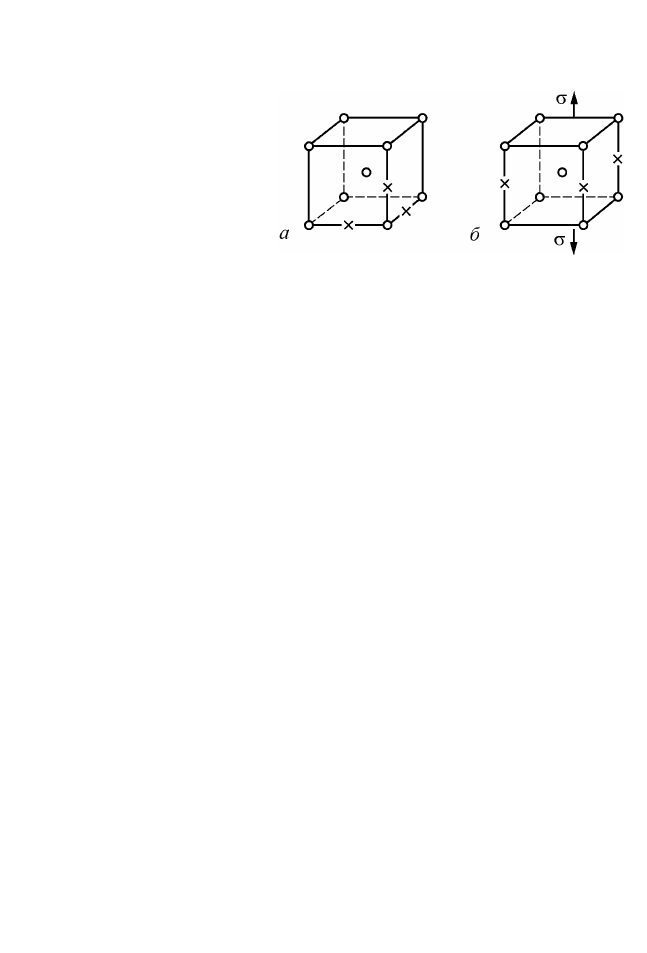
Атмосферы Снука. В ОЦК решетке железа при отсутствии на-

пряжений атомы углерода и азота с одинаковой вероятностью за-

полняют октаэдрические пустоты вдоль трех различных кристал-

лографических осей (рис. 2.51). Приложенные внешние напряже-

ния слегка увеличивают расстояние между двумя атомами железа

вдоль одного из направлений, и тогда атомы внедрения распола-

гаются преимущественно в этом направлении. Такой эффект упо-

рядочения в расположении атомов (эффект Снука) должен на-

блюдаться и в поле напряжений вокруг краевой и винтовой дис-

локаций. Область упорядоченного расположения примесных ато-

мов внедрения вокруг линии дислокации называют атмосферой

Снука. Ее образование уменьшает свободную энергию кристалла.

В отличие от несравненно более медленного образования атмо-

сферы Коттрела, связанного с диффузией атомов на значительные

252

расстояния, упорядочение Снука быстро возникает при переско-

ках атомов из одних октаэдрических пустот в соседние октаэдри-

ческие пустоты.

Рис. 2.51. Расположение

атомов внедрения (×)

в октаэдрических пустотах ОЦК

структуры без напряжений (а)

и при растягивающих

напряжениях (б)

Атмосферы Сузуки. В ГЦК решетке дефект упаковки расщеп-

ленной дислокации является тонкой прослойкой с чередованием

слоев, характерным для ГПУ решетки. Растворимость элемента в

общем случае должна быть разной в ГЦК и ГПУ решетках. При

достаточно высокой температуре атомы перераспределяются

диффузионным путем между дефектом упаковки и ГЦК решеткой

аналогично перераспределению элементов между двумя фазами.

Поэтому такое перераспределение атомов было названо Сузуки

химическим взаимодействием расщепленной дислокации с рас-

творенными атомами. Примесные атомы или диффундируют в

дефект упаковки, или уходят из него, при этом средняя концен-

трация в основном объеме с ГЦК решеткой остается практически

постоянной. Измененную концентрацию примесных атомов или

атомов легирующего элемента в дефекте упаковки растянутой

дислокации называют атмосферой Сузуки.

Взаимодействие дислокаций с вакансиями и межузельными

атомами. Поле напряжений краевой дислокации взаимодействует

с полем упругих напряжений вакансии и межузельного атома. Ме-

жузельный атом притягивается к области гидростатического рас-

тяжения, а вакансия – к области гидростатического сжатия. Упру-

гое взаимодействие вакансий с дислокациями слабее. Вакансии и

межузельные атомы, притянувшись к дислокации, могут аннигили-

ровать на порогах. Результат взаимодействия краевой дислокации

с примесными атомами принципиально отличен от результата ее

взаимодействия с вакансиями и межузельными атомами основного

металла. Если последние могут аннигилировать, то примесные

253

254

атомы сохраняют свою индивидуальность, образуя атмосферы. Ес-

ли скорость подхода вакансий и межузельных атомов к дислока-

ции больше скорости исчезновения их на порогах, то эти дефекты

могут образовать атмосферу вокруг линии дислокации типа кот-

трелловской примесной атмосферы.

Электрическое взаимодействие дислокации с атомами при-

меси. Энергия связи краевой дислокации с примесными атомами

обусловлена не только упругим (коттрелловским) взаимодейст-

вием, но и электрическим взаимодействием и взаимодействием с

неупругими искажениями в ядре дислокации.

Область разрежения вблизи края экстраплоскости из-за избыт-

ка электронов имеет слабый отрицательный заряд, а область сжа-

тия – положительный. Краевая и смешанная дислокации являются

слабым электрическим линейным диполем. Поэтому существует

электрическое взаимодействие между дислокацией и примесными

атомами, несущими заряд. Это взаимодействие было оценено ко-

личественно. В металлах электрическое взаимодействие дислока-

ции с примесным атомом значительно слабее, чем упругое.

Вклад неупругого взаимодействия в ядре дислокации количе-

ственно не оценен. Ошибка в расчетах энергии взаимодействия,

основанных на теории упругости, составляет 10%, если примесный

атом удален на два межатомных расстояния от ядра, и 50%, если он

удален на одно межатомное расстояние. Общее и весьма прибли-

женное представление о величине энергии связи краевой дислока-

ции с точечными дефектами разного вида дает табл. 2.6 (точечный

дефект удален от дислокации на одно межатомное расстояние).

Таблица 2.6

Энергия связи точечных дефектов с краевой дислокацией

Точечный дефект Е

упр.

эВ Е

эл.

эВ

Межузельный атом

Атом замещения

Вакансия

0,2-0,5

0,05 – 0,1

0,02

Примесные атомы внедрения значительно сильнее притягива-

ются к дислокации, чем атомы замещения.

2.2.4. Образование дислокаций

Механизм образования дислокаций – один из наименее изучен-

ных вопросов теории несовершенств кристаллической решетки.

До сих пор этот вопрос находится на стадии рабочих гипотез. Не-

которые из них получили косвенные экспериментальные подтвер-

ждения и на сегодня кажутся весьма логичными. Другие гипотезы,

ранее казавшиеся убедительными, теперь полностью или частично

отвергнуты. У исследователей нет единой точки зрения по поводу

механизма образования дислокаций. Ясно лишь, что дислокации

могут образовываться разными способами.

Энергия дислокации длиной порядка параметра решетки со-

ставляет несколько электрон-вольт. Поэтому термическая акти-

вация не может помочь образованию дислокаций.

Сразу же после кристаллизации металлические моно- и поли-

кристаллы содержат, как правило, большое число дислокаций.

Следовательно, дислокации могут возникать непосредственно у

фронта кристаллизации или же при охлаждении кристаллов после

исчезновения жидкой фазы. Ниже кратко рассмотрено несколько

возможных механизмов образования дислокаций.

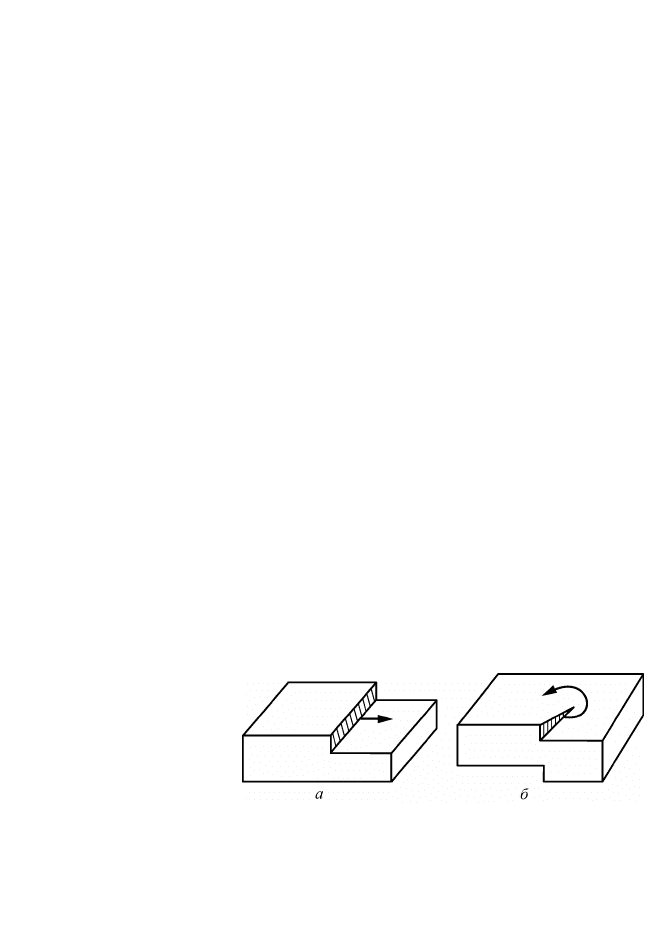
На фронте кристаллизации легко себе представить образование

винтовой дислокации. Когда кристалл, не содержащий дислока-

цию, растет путем присоединения атомов к ступеньке на первом

слое, то этот слой, полностью достраиваясь, сам себя изживает

(рис. 2.52,а).

Рис. 2.52. Ступенька на

поверхности совершенного

кристалла (а) и кристалла с

винтовой дислокацией (б)

Для образования нового атомного слоя требуется возникно-

вение на гладкой поверхности кристалла «двумерного» зароды-

ша, что является самым узким звеном процесса роста совершен-

ного кристалла и требует больших пересыщений (переохлажде-

ний).

255

256

Это звено отсутствует, если растет кристалл, содержащий вин-

товую дислокацию (рис. 2.52,б).

Присоединение атомов к ступеньке на его поверхности приво-

дит к вращению ступеньки. Поскольку атомы укладываются на

винтовую поверхность, то ступенька все время продолжает суще-

ствовать, облегчая тем самым присоединение атомов к кристаллу

и рост кристалла.

Кристалл, содержащий винтовую дислокацию, представляет со-

бой атомную плоскость, закрученную по спирали. Как же возника-

ет такое закручивание в первый момент роста, при образовании

зародыша?

Известно, что, как правило, зарождение кристаллов не само-

произвольно. Кристаллы зарождаются (гетерогенно) на готовой

подложке, которой служат стенки изложницы и мельчайшие твер-

дые частицы, взвешенные в расплаве. На поверхность таких под-

ложек выходят винтовые дислокации, т.е. здесь имеются готовые

ступеньки, к которым и присоединяются атомы из кристалли-

зующегося расплава. Таким образом, винтовая дислокация из

подложки как бы «прорастает» в образующийся кристалл.

Другая причина зарождения дислокаций в период кристалли-

зации – возникновение напряжений. Когда происходит ориентиро-

ванное нарастание (эпитаксия) кристалла на подложку, то сопря-

жение двух решеток из-за имеющегося всегда небольшого их не-

соответствия вызывает упругие напряжения в подложке и эпитак-

сиальном слое. Когда толщина эпитаксиального слоя достигает

некоторой критической величины, компенсация несоответствия

решеток подложки и растущего кристалла становится энергетиче-

ски выгодной не только в результате упругой деформации по всей

поверхности сопряжения двух решеток, а частично за счет дисло-

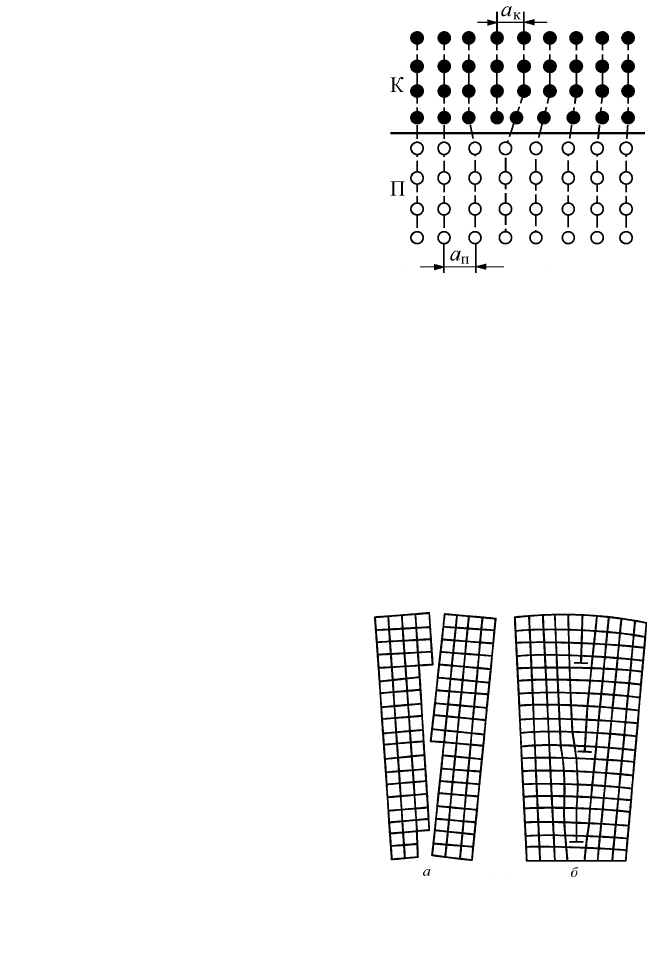
каций, возникающих на этой поверхности (рис. 2.53). Такие дисло-

кации называют структурными, эпитаксиальными или дислока-

циями несоответствия. Чем больше степень несоответствия двух

решеток, тем выше плотность эпитаксиальных дислокаций. По-

вышение энергии из-за образования дислокаций компенсируется

снижением энергии упругой деформации сопряженных решеток.

Из-за сегрегации примесей при кри-

сталлизации образуются смежные слои

разного состава с несколько различаю-

щимися межатомными расстояниями.

Эта разница вызывает появление упру-

гих напряжений. При определенной

разнице в межатомных расстояниях

соседних слоев энергетически выгод-

ным может стать их сопряжение с уча-

стием структурных дислокаций на гра-

нице между соседними слоями.

257

Дислокации могут возникать во

время кристаллизации с образованием

ячеистой структуры, а также вследст-

вие разных случайностей при росте

кристаллов. Эти случайности приводят к образованию мозаичной

структуры – кристалл состоит из субзерен (блоков), слегка взаимно

разориентированных. Одна из возможных причин образования суб-

зерен – изгиб очень «нежных» ветвей дендрита из-за конвекцион-

ных токов, градиента температур и действия других факторов. Ко-

гда слегка разориентированные ветви одного дендрита срастаются,

на границе между ними возникают дислокации.

Рис. 2.53. Дислокация

несоответствия на границе

растущего кристалла К

с подложкой П

На рис. 2.54,а показан простейший случай срастания двух сим-

метрично разориентированных час-

тей одного кристалла (или разных

кристаллов). Вертикальные атомные

плоскости в месте срастания не до-

ходят до низа кристалла. Вокруг края

каждой такой плоскости находится

краевая дислокация. На рис. 2.54,б

поверхность срастания представляет

собой стенку из положительных

дислокаций.

Рис. 2.54. Образование стенки

дислокаций при срастании

зерен во время кристаллизации

Дислокации могут также возни-

кать в полностью затвердевшем ме-

талле в непосредственной близости

от фронта кристаллизации и вдали

258

от него. Считается, что основным здесь является вакансионный

механизм образования дислокаций. Равновесная концентрация

вакансий резко уменьшается с понижением температуры от точки

кристаллизации. При ускоренном охлаждении кристалл сильно

пересыщается вакансиями. Избыточные вакансии конденсируют-

ся в дискообразные образования, параллельные плоскости плот-

нейшей упаковки. Диск может быть толщиной в один, два или

три слоя вакансий. Когда диаметр вакансионного диска превыша-

ет некоторую критическую величину, то под действием сил меж-

атомного притяжения его стороны сближаются, и в результате

захлопывания диска образуется краевая дислокация.

Захлопывание дисков вакансий с образованием дислокацион-

ных петель происходит не только при ускоренном охлаждении по

окончании кристаллизации, но, естественно, и при охлаждении по-

сле специального нагрева под закалку. При облучении металлов

дислокационные петли возникают на границах плоских скоплений

межузельных атомов и вакансий.

Дислокации зарождаются при концентрации напряжений в от-

дельных участках кристалла (около включений, трещин, границ

двойников и др.) до величин порядка G/30. Например, при охлаж-

дении металла из-за разного термического сжатия включения и

кристалла около их поверхности раздела могут возникнуть упру-

гие напряжения, достаточные для самопроизвольного зарождения

дислокационных петель. При зарождении дислокационных петель

и удаления их от включения происходит релаксация (разрядка)

напряжений.

Увеличение плотности дислокаций на несколько порядков в

результате холодной пластической деформации требует введения в

теорию представлений о механизме образования дислокаций в

процессе пластической деформации.

Размножение дислокаций при пластической деформации

(источник Франка–Рида). Весьма остроумный и простой меха-

низм размножения дислокаций в процессе пластической деформа-

ции был предложен Франком и Ридом (1950 г.). Источником дисло-

каций является дислокация, концы которой закреплены. На рис. 2.55

плоскость чертежа является плоскостью скольжения краевой дис-

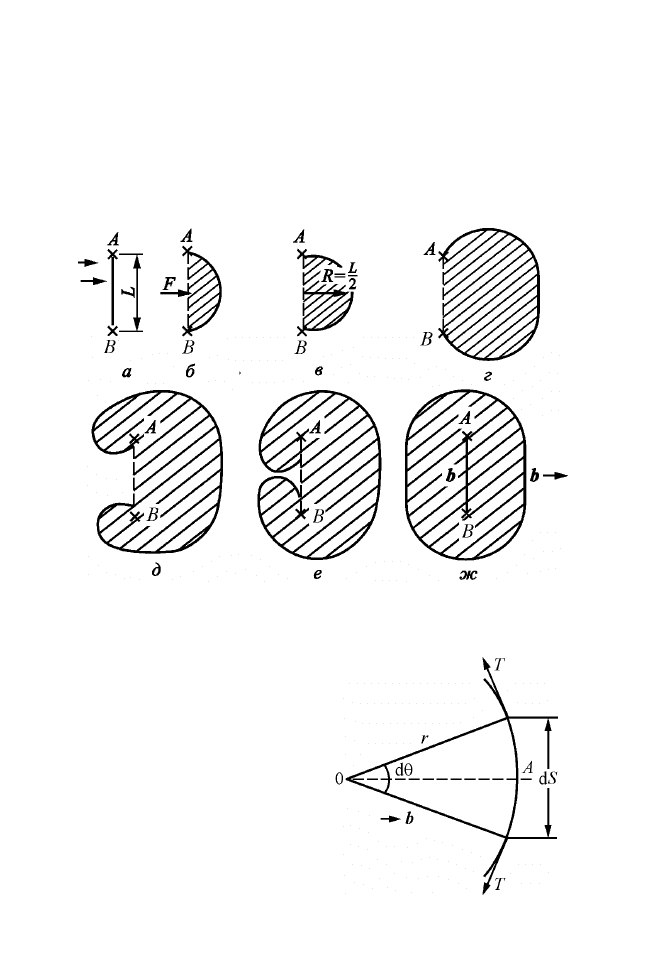
локации АВ. Приложенные однородные напряжения τ выгибают

линию дислокации в дугу. Так как дислокация обладает некоторой

энергией на единицу длины, она стремится уменьшить свою длину,

иначе говоря, вдоль линии дислокации действует некое натяжение.

Точно определить это линейное натяжение нелегко, поскольку уп-

ругая энергия содержится в ее поле напряжений. В рамках прибли-

жения линейное натяжение, определяемое как увеличение энергии

на единицу длины линии дислокации, можно выразить T = αGb

Рис. 2.55. Последовательные этапы работы дислокационного источника

Франка–Рида: стартовое (а), промежуточные (б–е) и конечное (ж) состояния.

Заштрихована площадь, заметаемая дислокацией при движении

Рис. 2.56. Равновесная форма

сегмента дислокации длиной dS при

действии на кристалл касательных

напряжений τ, параллельных

вектору Бюргерса

Рассмотрим изогнутую дислокацию (рис. 2.56). Линейное натя-

жение дислокации будет вызывать силу, стремящуюся выпрямить

259

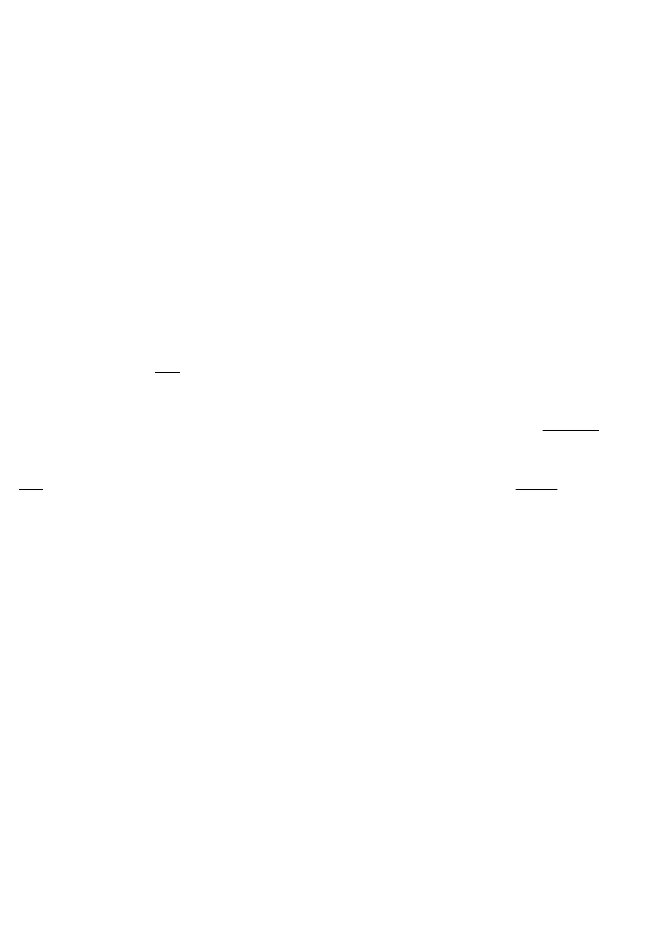
линию дислокации, и таким образом уменьшить ее общую энер-

гию. Эта сила перпендикулярна к линии дислокации и направлена

по радиусу к центру кривизны. Линия дислокации остается изогну-

той только в том случае, если будут существовать скалывающее

напряжение и соответствующая сила, которая действует на линию

дислокации и направлена в противоположную сторону. Чтобы най-

ти напряжение при данном радиусе кривизны, рассмотрим элемен-

тарную дугу дислокационной линии с вектором b.

Центральный угол, соответствующий этой дуге, равен dθ = dS/r.

Сила вдоль радиуса ОА, направленная наружу и возникающая при

приложении напряжения, действующего на элементарный отрезок

дислокации, равна F =

bdS. Сила противоположного знака, вы-

званная линейным натяжением Т на концах элементарной дуги,

равна F = 2Tsin

. При малых величинах dθ она будет равна Tdθ.

Равновесие наступит в том случае, если Tdθ = τbdS; T =

θτ

, τ =

или, подставляя значение Т = αGb

, получим τ =

Gbα

. Это на-

пряжение необходимо, чтобы изогнуть дислокацию до радиуса r.

По мере роста касательного напряжения дуга все больше выги-

бается и радиус ее уменьшается. Когда дуга становится полуок-

ружностью, ее радиус r = l/2, где l – длина дислокации. Это мини-

мальный радиус, и ему соответствует максимальное значение каса-

тельного напряжения τ

кр

= 2αGbL/l. Принимая α = 0,5, получим

кр

= Gb/l.

При любых значениях τ < τ

кр

дуга стабильна: определенному

значению τ соответствует определенное значение r. Если дуга еще

не выгнулась в полуокружность, то при уменьшении приложенно-

го напряжения сила натяжения будет упруго выпрямлять дугу.

Площадь, через которую продвигается дислокация, заштрихован-

ная на рис. 2.55, является зоной, где сдвиг уже прошел. Направле-

ние приложенного напряжения остается все время неизменным, а

сила f = tb, действующая на дислокацию, в каждой точке перпен-

дикулярна линии дислокации, т.е. направлена по радиусу кривой.

260