John R. Fanchi - Principles of Applied Reservoir Simulation, Second Edition
Подождите немного. Документ загружается.


42
Principles
of
Applied
Reservoir
Simulation
dx\
-'
jfl
,<,K
^c
I
(5,12)
*
i
The
derivative
(dxidi)
Sw
is the
velocity
of the
moving plane
S
w
,
and
(dfJdS
w
)
Sw
is
the
slope
of the
fractional
flow
curve.
The
integral
of the
frontal
advance
equation
gives
r
-
W
<
(
dL
\
s
-~7*
\7s~l
(5J3)
\
'
$„
where
x
Sw
distance traveled
by a
particular
S
w
contour [ft]
Wj
cumulative water
injected
[cu ft]
(df
w
/dsj\
slope
of
fractional
flow
curve
Water Saturation Profile
A
plot
of
S
w
versus distance using
Eq.
(5.13)
and
typical fractional
flow
curves leads
to the
physically impossible situation
of
multiple values
of
S
w
at
a
given location.
A
discontinuity
in
S
w
at a
cutoff location
x
c
is
needed
to
make
the
water saturation
distribution
single valued
and to
provide
a
material balance
for
wetting
fluids. The
procedure
is
described
by
Collins
[
1961
] and
summarized
below.
5.2
Welge's Method
In
1952,
Welge
published
an
approach that
is
widely
used
to
perform
the
Buckley-Leverett
frontal
advance calculation.
Welge's
approach
is
best
demonstrated using
a
plot
off
w
vs
S
w
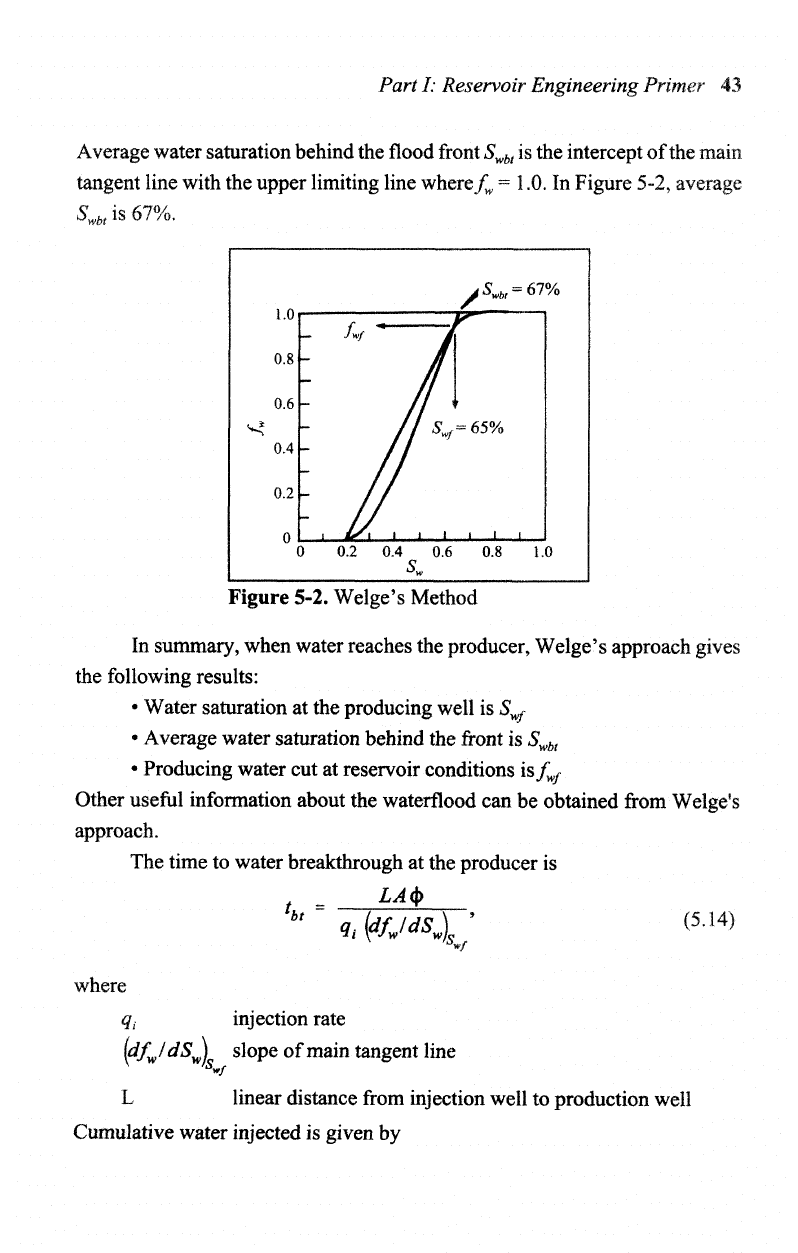
(Figure 5-2).
A
line
is
drawn
from
the
water saturation
S
w
before
the
waterflood
-
irreducible water saturation
S
wirr
- and
tangent
to a
point
on
thef
w
curve.
The
resulting tangent line
is
called
the
breakthrough tangent,
or
slope.
It is
illustrated
in
Figure 5-2. Water saturation
at the flood
front
S^is
the
point
of
tangency
on
thef
w
curve. Fractional
flow of
water
at the flood
front
is/^and
occurs
at the
point
of
tangency
S^
on
the/
w
curve.
In
Figure 5-2,
S
wf
\s
65%
and/
w/
is
95%
TEAM LinG - Live, Informative, Non-cost and Genuine!
Part
I:
Reservoir
Engineering
Primer
43
Average
water saturation behind
the flood
front
S
wbt
is the
intercept
of the
main
tangent line with
the
upper limiting line
where/,,
=
1.0.
In
Figure
5-2,
average
5^
is
67%.
0 0.2 0.4 0.6 0.8 1.0
Figure 5-2. Welge's Method
In
summary, when water reaches
the
producer,
Welge's
approach gives
the
following results:
•
Water saturation
at the
producing well
is
S
wf
•
Average water saturation behind
the front is
S
wbt
•
Producing water
cut at
reservoir conditions
isf
wf
Other
useful
information about
the
waterflood
can be
obtained
from
Welge's
approach.
The
time
to
water breakthrough
at the
producer
is
.
LA*
"
"
9,
(4W)
V
(5J4)
where
q
t
injection rate
(df
w
I
dS^\
slope
of
main tangent line
V
'
S
wf
L
linear distance
from
injection well
to
production well
Cumulative
water
injected
is
given
by
TEAM LinG - Live, Informative, Non-cost and Genuine!

44
Principles
of
Applied
Reservoir Simulation
Qi
=
where
Q
i
is the
cumulative pore volume
of
injected
water.
The
slope
of
the
water
fractional
flow
curve with respect
to
water saturation evaluated
at the
water
saturation
at
breakthrough gives
Q
(
at
breakthrough.
Effects
of
Capillary Pressure
and
Gravity
In
the
absence
of
capillary pressure
and
gravity
effects,
the flood front
propagates
as a
"sharp" step
function,
or
piston-like displacement.
The
presence
of
capillary pressure leads
to the
imbibition
of
water ahead
of the front.
This
causes
a
change
in the
behavior
of
produced
fluid
ratios. Rather than
an
abrupt
increase
in WOR
associated with piston-like displacement,
the WOR
will
increase gradually
as the
leading edge
of the
mobile water reaches
the
well
and
is
produced.
In
addition,
the WOR
will begin
to
increase sooner than
it
would
have
in the
absence
of
capillary pressure.
By
contrast, gravity causes high
S
w
values
to lag
behind
the front. The
result
is a
smeared
or
"dispersed"
flood front.
5.3
Miscible Displacement
Buckley-Leverett
theory treats
the
displacement
of one fluid by
another
under
immiscible, piston-like conditions.
An
immiscible displacement occurs
when
the
displaced
and
displacing
fluids do not
mix.
The
result
is a
readily
discernible interface between
the two fluids. In a
miscible displacement,
the
fluids
mix
and
the
interfacial
tension approaches zero
at
the
interface.
A
miscible
displacement system
is
described
by a
convection-dispersion (C-D) equation.
As
an
illustration, consider
the
one-dimensional
C-D
equation
for
the
concentra-
tion
C of the
displacing
fluid:
n
d
2
C
BC
dC
D
v
= —
f5
16\
dx
2
dx dt
IJ
'
10J
We
assume here that dispersion
D and
velocity
v are
real,
scalar constants.
The
diffusion
term
has the
Fickian
form
D'd
2
C/dx
2
and the
convection term
is
vdC/dx.
When
the
diffusion
term
is
much larger than
the
convection
term,
the
TEAM LinG - Live, Informative, Non-cost and Genuine!

Part
I:
Reservoir Engineering Primer
45
vdC/dx.
When
the
diffusion
term
is
much larger than
the
convection
term,
the
C-D
equation
behaves
like
the
heat conduction equation, which
is a
parabolic
partial
differential
equation (PDE).
If the
diffusion
term
is
much smaller than
the
convection term,
the C-D
equation behaves
like
a first-order
hyperbolic PDE.
The C-D
equation
is
especially valuable
for
studying numerical solutions
of
fluid flow
equations because
the C-D
equation
can be
solved
analytically
and
the
C-D
equation
may be
used
to
examine
two
important classes
of
PDEs
(parabolic
and
hyperbolic).
To
solve
the C-D
equation,
we
must
specify
two
boundary conditions
and an
initial condition.
The two
boundary conditions
are
needed because
the C-D
equation
is
second-order
in the
space derivative.
The
initial
condition satisfies
the
need
for a
boundary condition
in
time associated
with
the first-order
derivative
in
time.
The
boundary conditions
for the
miscibie
displacement
process
are
that
the
initial
concentration
of
displacing
fluid is
equal
to one at the
inlet
(x
=
0), and
zero
for all
other values
of
x. The
mathematical
expressions
for
these boundary conditions
are
concentration C(0,
t) =
I
at the
inlet, concentration
C(°°,
f)
= 0 at the
edge
of the
linear system
for all
times
t
greater than
the
initial time
t = 0, and the
initial
condition C(x,
0) = 0 for all
values
of
x
greater than
0.
The
propagation
of the
miscibie displacement
front
is
calculated
by
solving
the C-D
equation.
The
analytical solution
of the
one-dimensional
C-D
equation
is
[Peaceman,
1977]
C(jc,
0
=
-U
erfc
2
l
JC
- Vt
X
+ Vt
2
]
/Dt
where
the
complementary error
function
erfc(y)
is
defined
as
(5.17)
2
r
2
erfc(j)
= 1 - — je
z
rfz
(5,18)
V*
o
Abramowitz
and
Stegun
[
1972]
have presented
an
accurate numerical algorithm
for
calculating
the
complementary error
function
erfcO/).
A
comparison
of the
analytical
solution
of the C-D
equation with numerical solutions
is
given
in
Fanchi
[2000].
TEAM LinG - Live, Informative, Non-cost and Genuine!

46
Principles
of
Applied
Reservoir Simulation
Exercises
Exercise
5.1
Consider
an
oil-water
system
in
which
oil
viscosity
is
0.64
cp and
water
viscosity
is 0.5 cp. Oil
relative permeability
(k
row
)
and
water relative
permeability
(Ar
w
)
are
given
in the
following table
as a
function
of
water
saturation
(S
w
).
Complete
the
table
by
using
the
viscosity
and
relative permeabil-
ity
information
to
calculate
oil
mobility
(A,
0
),
water mobility
(A.
w
),
total mobility
(1,),
water fractional
flow
(/"„,),
and oil
fractional
flow
(£,).
Total mobility
is the
sum
of
oil
mobility
and
water mobility. Assume absolute permeability
is 100
md.
s
w
-
0.30
0.35
0.40
0.45
0.50
0.55
0.60
0.65
0.70
0.80
*n.
0.000
0.005
0.010
0.017
0.023
0.034
0.045
0.064
0.083
0.120
^
row
1.000
0.590
0.320
0.180
0.080
0.030
0.010
0.001
0.000
0.000
^
k
*,
L
L
Exercise
5.2
Plot
X
0
,
X
w
,
and A, in
Exercise
5.1
as a
function
of
S
w
.
What
is the
mobility
ratio
of the
oil-water system? Hint:
See Eq.
(3.14).
Exercise
5.3
Piotf
0
and/,,
in
Exercise
5.1
as a
function
of
S
w
.
Use the
plot
of
f
w
versus
S
w
and
Welge's
method
to
determine water saturation
at
the
producing
well,
average water saturation behind
the front, and
producing water
cut at
reservoir conditions.
TEAM LinG - Live, Informative, Non-cost and Genuine!

Part
I:
Reservoir Engineering Primer
47
Exercise
5.4 Run
EXAM3.DAT
and
plot water saturation
as a
function
of
distance between wells
at
the
midpoint
of
the
ran and
at
the end of
the
ran.
Hint:
water
saturation
is
reported
in the run
output
file
WTEMP.ROF.
TEAM LinG - Live, Informative, Non-cost and Genuine!

Chapter
6
Frontal
Stability
The
stability
of a flood
front
can
influence
the
efficiency
of fluid
displacement.
A front is
stable
if it
retains
the
shape
of the
interface between
displaced
and
displacing
fluids as the
front
moves through
the
medium.
An
analysis
of
frontal
stability
is
presented
in
this chapter
in
terms
of a
specific
example
-
the
advance
of
a
water-oil displacement
front in the
absence
of
gravity
and in the
presence
of
gravity.
The
stability
of the
front
is
then studied using
linear
stability analysis.
6.1
Frontal Advance Neglecting Gravity
The
displacement
of one
phase
by
another
may be
analytically studied
if
a
linear, homogenous porous medium
is
assumed.
Let us first
consider
the
displacement
of oil by
water
in a
horizontal porous medium
of
length
L. We
assume
piston-like displacement
of a
front
located
atx
f
.
Application
of
Darcy's
law
and the
continuity equation leads
to a
pressure distribution described
by
Poisson's equation.
The
absence
of
sources
or
sinks
in the
medium reduces
Poisson's
equation
to the
Laplace equation
for the
water phase
pressure:
£3
D
=
0,
0<x<x
r
(6.1)
dx
The
corresponding
equation
for oil
phase pressure
is
48
TEAM LinG - Live, Informative, Non-cost and Genuine!

ox
Part
I:
Reservoir Engineering Primer
49
3
f
= 0,
x
f
<
x < L
(62)
Equations
(6.1)
and
(6.2) apply
to
those parts
of the
medium containing water
and
oil
respectively.
They assume that
the fluids are
incompressible,
and
that
the
oil-water interface
is a
piston-like displacement
in the
^-direction.
The
piston-
like
displacement assumption implies
a
discontinuous change
from
mobile
oil
to
mobile water
at the
displacement
front.
This concept
differs
from the
Buckley-
Leverett
analysis
presented
in
Chapter
5.
Buckley-Leverett
theory with
Welge's
method shows
the
existence
of a
transition zone
as
saturations grade
from
mobile
oil
to
mobile water.
The
saturation
profile
at the
interface between
the
immiscible
phases
depends
on the
fractional
flow
characteristics
of the
system.
The
present
method
has
less structure
in the
saturation profile,
but is
more readily
suited
for
analyzing
the
stability
of the
displacement
front.
Boundary
conditions
at the
displacement
front
are
given
by
continuity
of
phase
pressure
P
0
=
P
w
at
x=x
f
(t)
(6.3)
and
continuity
of
phase velocity
(64)
where
A.J
is the
mobility
of
phase
0.
Equation (6.3)
is
valid when
we
neglect
capillary pressure,
and the
effect
of
gravity
has
been excluded
from
Eq.
(6.4).
The
exclusion
of
gravity corresponds physically
to flow in a
horizontal
medium.
Boundary
conditions
at the
edges
of the
porous medium
are
P
w
=P
l
atx=0
(6.5)
and
P
0
=
P
2
at*=
L
(6.6)
Equations
(6.1)
through (6.6)
may be
solved analytically.
We
begin
by
integrating Eqs.
(6.1)
and
(6.2)
to find the
general solutions
P
w
=
A
w
x+B
w
(6.7)
and
TEAM LinG - Live, Informative, Non-cost and Genuine!

50
Principles
of
Applied
Reservoir
Simulation
P
0
=
A
0
x+B
0
(6.8)
where
the
constant coefficients
{A
e
B
s
}
are
determined
by
applying
the
boundary
conditions.
Substituting
Eq.
(6.5)
in Eq.
(6.7) gives
B
w
=
P
{
(6.9)
The
remaining
coefficients
are
found
by
simultaneously solving Eqs.
(6.4),
(6,7),
and
(6.8) subject
to
Eqs.
(6.3),
(6.5),
and
(6.6).
The
resulting
coefficients
are
AP
A
w
=
-~rz—-———
(6.10)
ML
+ (1 -
M}x
f
A
0
=MA
W
(6.11)
B
0
=
PI
=
(A
w
-
A
0
)x
f
=
P,
+
(1-
M)A
w
x
f
(6.12)
where
M is the
mobility ratio
M=-~-
(6.13)
k
o
and
the
pressure difference
is
AP=P,-P
2
(6.14)
The
frontal
velocity
Vyis
given
by
dx
v
where
S
or
is
residual
oil
saturation,
S
wc
is
connate water saturation,
and
v
w
is the
Darcy
velocity:
V
w
~
~^w~A
=
~^w^w
(6.16)
Substituting
Eq.
(6.16)
into
(6.15)
gives
dt
~
An~
s
-
?
^F
i>rr
.
/,
m~l
(6.17)
-
A/)*,]
TEAM LinG - Live, Informative, Non-cost and Genuine!
Part
I:
Reservoir Engineering Primer
51
The
integral
of Eq.
(6.17)
with respect
to
time gives
the frontal
advance.
6.2
Frontal
Advance
Including
Gravity
Gravity
is
included
in the
analysis
of frontal
advance
in a
dipping
reservoir
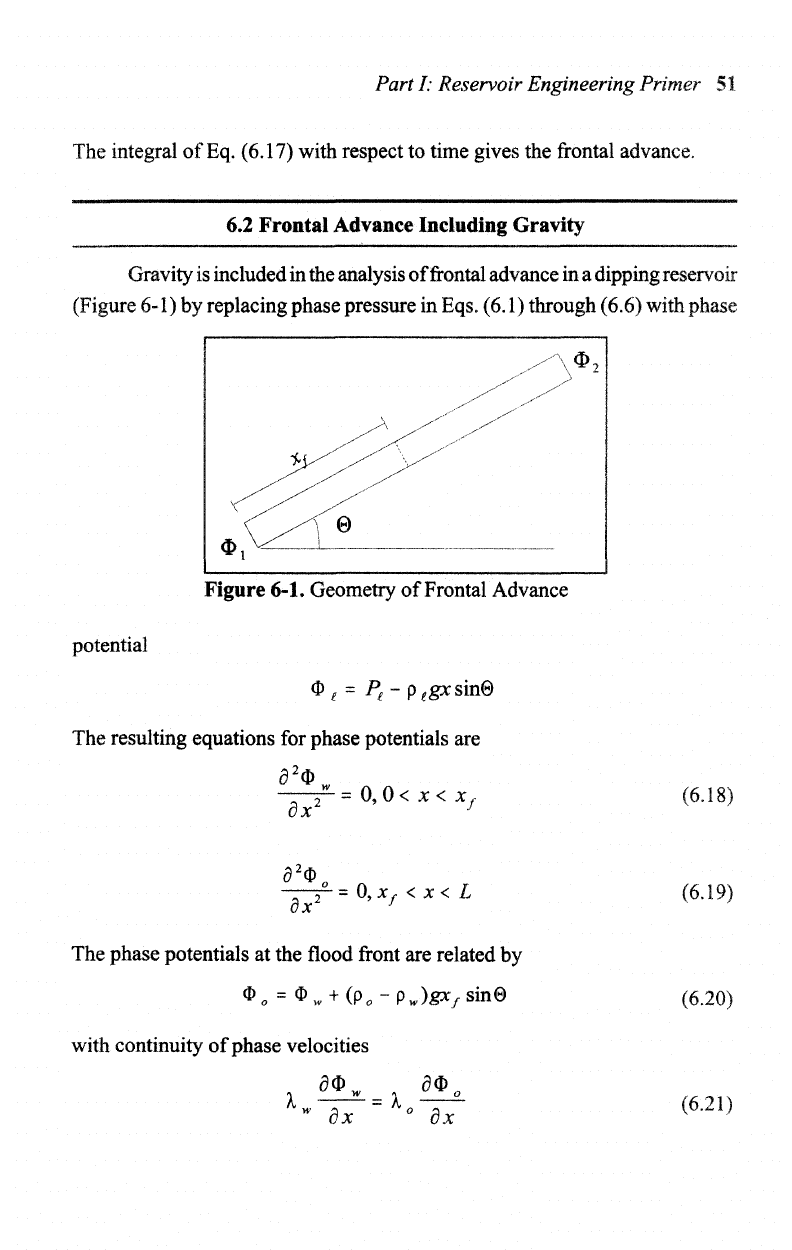
(Figure
6-1)
by
replacing phase pressure
in
Eqs.
(6.1)
through (6.6) with phase
Figure 6-1. Geometry
of
Frontal Advance
potential
<J>
;
=
P
f
- p
(
gxsm&
The
resulting equations
for
phase potentials
are
0,0<x<x
f
(6.18)
dx
2
d
2
®
(6.19)
->
—
\J)
A f
'X
J*.
^,
JL^
5jc
7
The
phase potentials
at the
flood
front are
related
by
with
continuity
of
phase
velocities
TEAM LinG - Live, Informative, Non-cost and Genuine!
