Jeanblanc M., Yor M., Chesney M. Mathematical Methods for Financial Markets
Подождите немного. Документ загружается.

6.2 Properties 347
6.2.4 Lamperti’s Theorem
We present a particular example of the relationship between exponentials
of L´evy processes and semi-stable processes studied by Lamperti [562]who
proved that (powers of) Bessel processes are the only semi-stable one-
dimensional diffusions. See also Yor [863, 865] and DeBlassie [228].
Theorem 6.2.4.1 The exponential of Brownian motion with drift ν ∈ R
+
can be represented as a time-changed BES
(ν)
.Moreprecisely,
exp(W
t
+ νt)=R
(ν)
t
0
exp[2(W
s
+ νs)] ds
where (R
(ν)
(t),t≥ 0) is a BES
(ν)
.
Remark that, thanks to the scaling property of the Brownian motion, this
result can be extended to exp(σW
t
+ νt). In that case
exp(σW
t
+ νt)=R
(ν/σ
2
)
σ
2
t
0
exp[2(σW
s
+ νs)] ds
.
Proof: Introduce the increasing process A
t
=
t
0
exp[2(W
s
+ νs)] ds and C
its inverse C
u
=inf{t ≥ 0:A
t
≥ u}.From
exp[2(W
s
+ νs)] = exp[2s(ν + W
s
/s)] ,
it can be checked that A
∞
= ∞ a.s., hence C
u
< ∞, ∀u<∞ and
C
∞
= ∞,a.s.. By definition of C,wegetA
C
t
= t =
C
t
0
exp[2(W
s
+ νs)] ds.
By differentiating this equality, we obtain dt = exp[2(W
C
t
+ νC
t
)]dC
t
.The
continuous process
W defined by
W
u
:=
C
u
0
exp(W
s
+ νs) dW
s
is a martingale with increasing process
C
u
0
exp[2(W
s
+νs)] ds = u. Therefore,
W is a Brownian motion. From the definition of C,
W
A
t
=
t
0
exp(W
s
+ νs) dW
s
.
This identity may be written in a differential form
d
W
A
t
=exp(W
t
+ νt) dW
t
.
We now prove that R
u
:=exp(W
C
u
+ νC
u
) is a Bessel process. Itˆo’s formula
gives
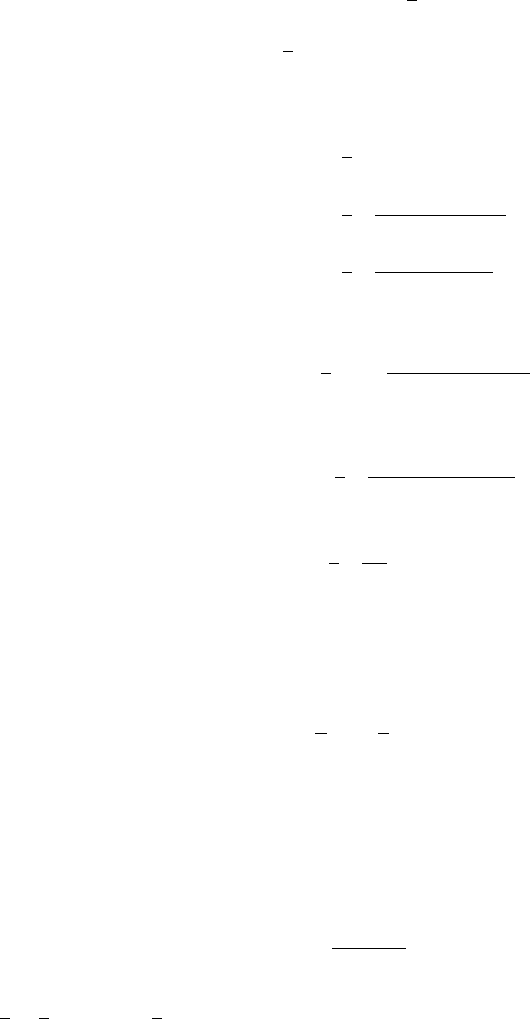
348 6 A Special Family of Diffusions: Bessel Processes
d[exp(W
t
+ νt)] = exp(W
t
+ νt)(dW
t
+ νdt)+
1
2
exp(W
t
+ νt)dt
= d
W
A
t
+
ν +
1
2
exp(W
t
+ νt)dt .
This equality can be written in an integral form
exp(W
t
+ νt)=1+
W
A
t
+
t
0
ν +
1
2
exp(W
s
+ νs)ds
=1+
W
A
t
+
t
0
ν +
1
2
exp 2(W
s
+ νs)
exp(W
s
+ νs)
ds
=1+
W
A
t
+
t
0
ν +
1
2
dA
s
exp(W
s
+ νs)
.
Therefore
exp(W
C
u
+ νC
u
)=1+
W
u
+
ν +
1
2
u
0
ds
exp(W
C
s
+ νC
s
)
.
Hence,
d exp(W
C
u
+ νC
u
)=d
W
u
+
ν +
1
2
du
exp(W
C
u
+ νC
u
)
that is,
dR
u
= d
W
u
+
ν +
1
2
du
R
u
.
The result follows from the uniqueness of the solution to the SDE associated
with the BES
(ν)
(see Definition 6.1.2.2), and from R
A
t
=exp(W
t
+ νt).
Remark 6.2.4.2 From the obvious equality
exp(σB
t
+ νt)=
exp
σ
2
B
t
+
ν
2
t
2
,
it follows that the exponential of a Brownian motion with drift is also a time-
changed Bessel squared process. This remark is closely related to the following
exercise.
Exercise 6.2.4.3 Prove that the power of a Bessel process is another Bessel
process time-changed:
q[R
(ν)
t
]
1/q
= R
(νq)
t
0
ds
[R
(ν)
s
]
2/p
where
1
p
+
1
q
=1,ν >−
1
q
.
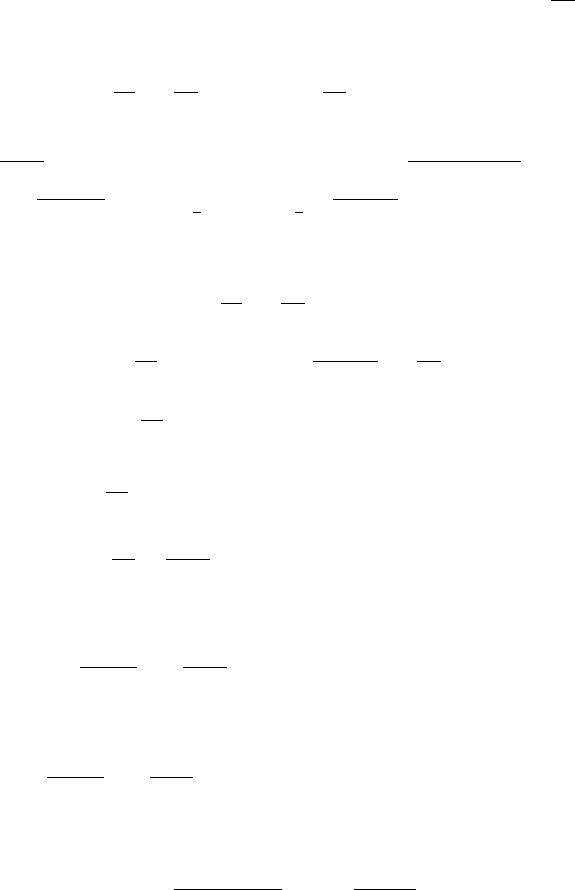
6.2 Properties 349
6.2.5 Laplace Transforms
In this section, we give explicit formulae for some Laplace transforms related
to Bessel processes.
Proposition 6.2.5.1 The joint Laplace transform of the pair
R
2
t
,
t
0
ds
R
2
s
satisfies
P
(ν)
r
exp
−aR
2
t
−
μ
2
2
t
0
ds
R
2
s
= P
(γ)
r
R
t
r
ν−γ
exp(−aR
2
t
)
(6.2.10)
=
r
γ−ν
Γ (α)
∞
0
dv v
α−1
(1 + 2(v + a)t)
−(1+γ)
exp
−
r
2
(v + a)
1+2(v + a)t
where γ =
μ
2
+ ν
2
and α =
1
2
(γ − ν)=
1
2
(
μ
2
+ ν
2
− ν).
Proof: From the absolute continuity relationship (6.1.5)
P
(ν)
r
exp
−aR
2
t
−
μ
2
2
t
0
ds
R
2
s
= P
(0)
r
R
t
r
ν
exp
−aR
2
t
−
μ
2
+ ν
2
2
t
0
ds
R
2
s
= P
(γ)
r
R
t
r
ν−γ
exp(−aR
2
t
)
.
The quantity P
(γ)
r
R
t
r
ν−γ
exp(−aR
2
t
)
can be computed as follows. From
1
x
α
=
1
Γ (α)
∞
0
dv exp(−vx)v
α−1
(6.2.11)
(see formula (A.5.8) in the appendix), it follows that
P
(γ)
r
1
(R
t
)
2α
=
1
Γ (α)
∞
0
dv v
α−1
P
(γ)
r
[exp(−vR
2
t
)] .
Therefore, for any α ≥ 0, the equality
P
(γ)
r
1
(R
t
)
2α
=
1
Γ (α)
1/2t
0
dv v
α−1
(1 − 2tv)
γ−α
exp(−r
2
v)
follows from the identity (6.2.1) written in terms of BES
(γ)
,
P
(γ)
r
[exp(−vR
2
t
)] =
1
(1 + 2vt)
1+γ
exp
−
r
2
v
1+2vt
, (6.2.12)
and a change of variable.
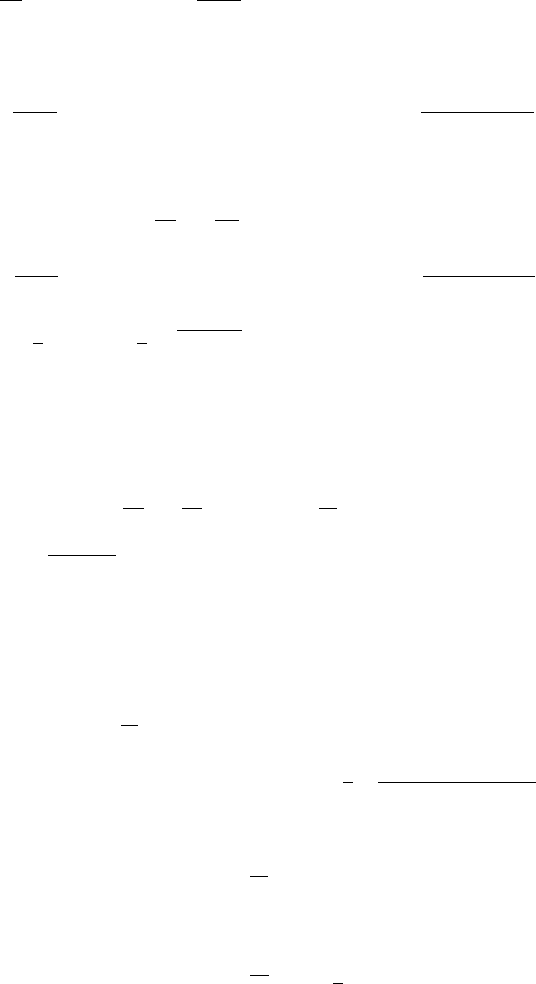
350 6 A Special Family of Diffusions: Bessel Processes
Using equality (6.2.11) again,
P
(γ)
r
1
R
t
2α
exp(−aR
2
t
)
=
1
Γ (α)
∞
0
dv v
α−1
P
(γ)
r
[exp(−(v + a)R
2
t
)] : = I.
The identity (6.2.12) shows that
I =
1
Γ (α)
∞
0
dv v
α−1
(1 + 2(v + a)t)
−(1+γ)
exp
−
r
2
(v + a)
1+2(v + a)t
.
Therefore
P
(ν)
r
exp
−aR
2
t
−
μ
2
2
t
0
ds
R
2
s
=
r
γ−ν
Γ (α)
∞
0
dv v
α−1
(1 + 2(v + a)t)
−(1+γ)
exp
−
r
2
(v + a)
1+2(v + a)t
where α =
1
2
(γ − ν)=
1
2
(
μ
2
+ ν
2
− ν).
We state the following translation of Proposition 6.2.5.1 in terms of
BESQ processes:
Corollary 6.2.5.2 The quantity
Q
(ν)
x
exp
−aρ
t
−
μ
2
2
t
0
ds
ρ
s
= Q
(γ)
x
ρ
t
x
(ν−γ)/2
exp(−aρ
t
)
(6.2.13)
where γ =
μ
2
+ ν
2
is given by (6.2.10).
Another useful result is that of the Laplace transform of the pair (ρ
t
,
t
0
ρ
s
ds)
under Q
δ
x
.
Proposition 6.2.5.3 For a BESQ
δ
, we have for every λ>0,b=0
Q
δ
x
exp(−λρ
t
−
b
2
2
t
0
ρ
s
ds)
(6.2.14)
=
cosh(bt)+2λb
−1
sinh(bt)
−δ/2
exp
−
1
2
xb
1+2λb
−1
coth(bt)
coth(bt)+2λb
−1
.
Proof: Let ρ be a BESQ
δ
process starting from x:
dρ
t
=2
√
ρ
t
dW
t
+ δdt.
Let F : R
+
→ R be a locally bounded function. The process Z defined by
Z
u
: = exp
u
0
F (s)
√
ρ
s
dW
s
−
1
2
u
0
F
2
(s)ρ
s
ds
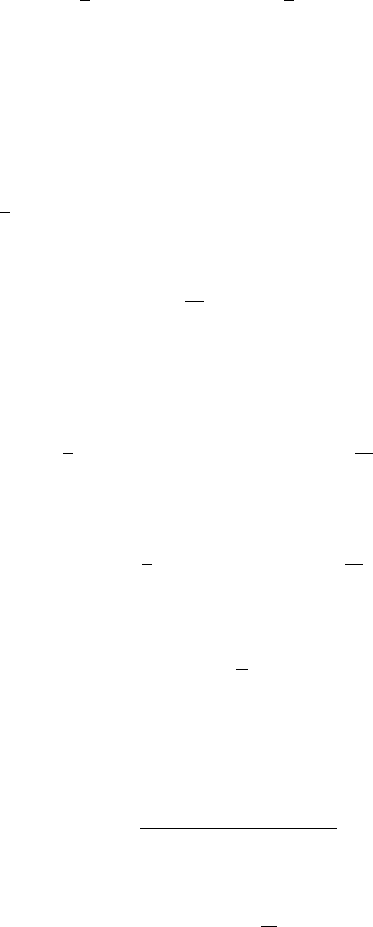
6.2 Properties 351
is a local martingale. Furthermore,
Z
u
=exp
1
2
u
0
F (s)d(ρ
s
− δs) −
1
2
u
0
F
2
(s)ρ
s
ds
.
If F has bounded variation, an integration by parts leads to
u
0
F (s)dρ
s
= F (u)ρ
u
− F (0)ρ
0
−
u
0
ρ
s
dF (s)
and
Z
u
=exp
1
2
F (u)ρ
u
− F (0)x −
u
0
(δF (s)+F
2
(s)ρ
s
)ds + ρ
s
dF (s)
.
Let t be fixed. We now consider only processes indexed by u with u ≤ t.
Let b be given and choose F =
Φ
Φ
where Φ is the decreasing solution of
Φ
= b
2
Φ, on [0,t]; Φ(0) = 1; Φ
(t)=−2λΦ(t) ,
where Φ
(t) is the left derivative of Φ at t. Then,
Z
u
=exp
1
2
(F (u)ρ
u
− F (0)x − δ ln Φ(u)) −
b
2
2
u
0
ρ
s
ds
is a bounded local martingale, hence a martingale. Moreover,
Z
t
=exp
−λρ
t
−
1
2
(Φ
(0)x + δ ln Φ(t)) −
b
2
2
t
0
ρ
s
ds
and 1 = E(Z
t
), hence the left-hand side of equality (6.2.14)isequalto
(Φ(t))
δ/2
exp
x
2
Φ
(0)
.
The general solution of Φ
= b
2
Φ is Φ(s)=c
1
sinh(bs)+c
2
cosh(bs),
and the constants c
i
,i =1, 2 are determined from the boundary conditions.
The boundary condition Φ(0) = 1 implies c
2
= 1 and the condition Φ
(t)=
−2λΦ(t) implies
c
1
= −
b sinh(bt)+2λ cosh(bt)
b cosh(bt)+2λ sinh(bt)
.
Remark 6.2.5.4 The transformation F =
Φ
Φ
made in the proof allows us to
link the Sturm-Liouville equation satisfied by Φ to a Ricatti equation satisfied
by F . This remark is also valid for the general computation made in the
following Exercise 6.2.5.8 .

352 6 A Special Family of Diffusions: Bessel Processes
Corollary 6.2.5.5 As a particular case of the equality (6.2.14), one has
Q
δ
0
exp(−
b
2
2
t
0
ρ
s
ds)
= (cosh(bt))
−δ/2
.
Consequently, the density of
1
0
ρ
s
ds is
f(u)=2
δ/2
∞
n=0
α
n
(δ/2)
2n + δ/2
√
2πu
3
e
−
1
2u
(2n+δ/2)
2
,
where α
n
(x) are the coefficients of the series expansion
(1 + a)
−x
=
∞
n=0
α
n
(x)a
n
.
Proof: From the equality (6.2.14),
E
exp
−
b
2
2
1
0
ρ
s
ds
= (cosh(b))
−δ/2
= e
−bδ/2
2
δ/2
(1 + e
−2b
)
δ/2
=2
δ/2
∞
n=0
α
n
(δ/2)e
−2bn
e
−bδ/2
.
Using
e
−ba
=
∞
0
dt
a
√
2πt
3
e
−a
2
/(2t)−b
2
t/2
dt
we obtain
E
exp
−
b
2
2
1
0
ρ
s
ds
=2
δ/2
n
α
n
δ
2
∞
0
2n + δ/2
√
2πt
3
e
−(2n+δ/2)
2
/(2t)−b
2
t/2
dt
and the result follows.
Comment 6.2.5.6 See Pitman and Yor [720] for more results of this kind.
Exercise 6.2.5.7 Prove, using the same method as in Proposition 6.2.5.1
that
P
(ν)
r
1
R
α
t
exp
−
μ
2
2
t
0
ds
R
2
s
= P
(0)
r
R
ν
t
r
ν
R
α
t
exp
−
μ
2
+ ν
2
2
t
0
ds
R
2
s
= P
(γ)
r
R
ν−γ−α
t
r
ν−γ
,
and compute the last quantity.
6.2 Properties 353
Exercise 6.2.5.8 We shall now extend the result of Proposition 6.2.5.3 by
computing the Laplace transform
Q
δ
x
exp
−λ
t
0
duφ(u)ρ
u
.
In fact, let μ be a positive, diffuse Radon measure on R
+
. The Sturm-Liouville
equation Φ
= μΦ has a unique solution Φ
μ
, which is positive, decreasing on
[0, ∞[andsuchthatΦ
μ
(0) = 1. Let Ψ
μ
(t)=Φ
μ
(t)
t
0
ds
Φ
2
μ
(s)
.
1. Prove that the function Ψ
μ
is a solution of the Sturm-Liouville equation,
such that Ψ
μ
(0) = 0,Ψ
μ
(0) = 1, and the pair (Φ
μ
,Ψ
μ
) satisfies the
Wronskian relation
W (Φ
μ
,Ψ
μ
)=Φ
μ
Ψ
μ
− Φ
μ
Ψ
μ
=1.
2. Prove that, for every t ≥ 0:
Q
δ
x
exp
−
1
2
t
0
ρ
s
dμ(s)+λρ
t
=
1
Ψ
μ
(t)+λΨ
μ
(t)
δ/2
exp
x
2
Φ
μ
(0) −
Φ
μ
(t)+λΦ
μ
(t)
Ψ
μ
(t)+λΨ
μ
(t)
,
and
Q
δ
x
exp
−
1
2
∞
0
ρ
s
dμ(s)
=(Φ
μ
(∞))
δ/2
exp
x
2
Φ
μ
(0)
.
3. Compute the solution of the Sturm Liouville equation for
μ(ds)=
λ
(a + s)
2
ds, (λ, a > 0)
(one can find a solution of the form (a+s)
α
where α is to be determined).
See [RY] or Pitman and Yor [717] for details of the proof and Carmona [140]
and Shirakawa [790] for extension to the case of Bessel processes with time-
dependent dimension.
6.2.6 BESQ Processes with Negative Dimensions
As an application of the absolute continuity relationship (6.1.6), one obtains
Lemma 6.2.6.1 Let δ ∈] −∞, 2[ and Φ a positive function. Then, for any
x>0
Q
δ
x
Φ(ρ
t
)1
{T
0
>t}
= x
1−
δ
2
Q
4−δ
x
Φ(ρ
t
)(ρ
t
)
δ
2
−1
.

354 6 A Special Family of Diffusions: Bessel Processes
Definition 6.2.6.2 The solution to the equation
dX
t
= δdt+2
|X
t
|dW
t
,X
0
= x
where δ ∈ R, x ∈ R is called the square of a δ-dimensional Bessel process
starting from x.
This equation has a unique strong solution (see [RY], Chapter IX, Section
3). Let us assume that X
0
= x>0andδ<0. The comparison theorem
establishes that this process is smaller than the process with δ = 0, hence, the
point 0 is reached in finite time. Let T
0
be the first time when the process X
hits the level 0. We have
X
t
:=X
T
0
+t
= δt +2
T
0
+t
T
0
|X
s
|dW
s
,t≥ 0 .
Setting γ = −δ and
W
s
= −(W
s+T
0
− W
T
0
), we obtain
−
X
t
= γt +2
t
0
|
X
s
|d
W
s
,t≥ 0 ,
hence, if Y
t
= −
X
t
we get
Y
t
= γt +2
t
0
|Y
s
|d
W
s
,t≥ 0 .
This is the SDE satisfied by a BESQ
γ
0
, hence −X
T
0
+t
is a BESQ
γ
0
.ABESQ
δ
x
process with x<0andδ<0 behaves as minus a BESQ
−δ
−x
and never becomes
strictly positive.
One should note that the additivity property for BESQ with arbitrary
(non-positive) dimensions does not hold. Indeed, let δ>0 and consider
X
t
=2
t
0
|X
s
|dβ
s
+ δt
Y
t
=2
t
0
|Y
s
|dγ
s
− δt
where β and γ are independent BM’s, then, if additivity held, (X
t
+Y
t
,t≥ 0)
would be a BESQ
0
0
, hence it would be equal to 0, so that X = −Y ,whichis
absurd.
Proposition 6.2.6.3 The probability transition of a BESQ
−γ
x
, γ>0 and
x ≥ 0 is Q
−γ
x
(X
t
∈ dy)=q
−γ
t
(x, y)dy where
q
−γ
t
(x, y)=q
4+γ
t
(y, x) , for y>0
= k(x, y, γ, t)e
−a−b
∞
0
(z +1)
m
z
m
e
−bz−
a
z
dz , for y<0

6.2 Properties 355
where
k(x, y, γ, t)=
Γ
γ
2
−2
2
−γ
γ
x
1+m
|y|
m−1
t
−γ−1
and
m =
γ
2
,a=
|y|
2t
,b=
x
2t
.
Proof: We decompose the process X before and after its hitting time T
0
as
follows:
Q
−γ
x
[f(X
t
)] = Q
−γ
x
[f(X
t
)1
{t<T
0
}
]+Q
−γ
x
[f(X
t
)1
{t>T
0
}
] .
From the time reversal, using Lemma 6.2.6.1 and noting that
y
x
−1−
γ
2
q
4−γ
t
(x, y)=q
4+γ
t
(y, x)
we obtain
(X
t
,t≤ T
0
)
law
=(
X
γ
x
−t
,t≤ γ
x
)
where
X is a BESQ
4+γ
0
process and γ
x
=sup{t :
X
t
= x}. It follows that
Q
−γ
x
[f(X
t
)1
{t<T
0
}
]=Q
4+γ
0
[f(
X
γ
x
−t
)1
{t<γ
x
}
]
=
∞
t
q
x
(s)Q
4+γ
0
[f(X
s−t
)|X
s
= x]ds
where q
x
(s)ds = Q
4+γ
0
(γ
x
∈ ds). Then, some standard computation leads to
Q
4+γ
0
[f(X
s−t
)|X
s
= x]=
f(y)
q
4+γ
s−t
(0,y) q
4+γ
t
(y, x)
q
4+γ
s
(0,x)
dy, s>t.
From the study of the last passage times (see equality (5.6.2)) one obtains
q
x
(s)=
1
sΓ (ν)
x
2s
ν
e
−x/(2s)
=(2+γ)q
4+γ
s
(0,x) . (6.2.15)
Hence
Q
−γ
x
[f(X
t
)1
{t<T
0
}
]=
∞
t
ds(2 + γ)
∞
0
f(y)q
4+γ
s−t
(0,y)q
4+γ
t
(y, x)dy
and using Fubini’s theorem
Q
−γ
x
[f(X
t
)1
{t<T
0
}
]=
∞
0
f(y)q
4+γ
t
(y, x)dy .
The computation of Q
−γ
x
[f(X
t
)1
{t>T
0
}
] is carried out using (6.2.15)and
Q
−γ
x
[T
0
∈ ds]=q
x
(s)ds. One obtains
Q
−γ
x
[f(X
t
)1
{t>T
0
}
]=
t
0
(γ +2)q
4+γ
s
(0,x)q
γ
t−s
(0, −y)ds .
356 6 A Special Family of Diffusions: Bessel Processes
Exercise 6.2.6.4 Prove that, for δ>2, the default of martingality of R
2−δ
(where R is a Bessel process of dimension δ starting from x) is given by
E(R
2−δ
0
− R
2−δ
t
)=x
2−δ
P
4−δ
(T
0
≤ t) .
Hint: Prove that
E(R
2−δ
t
)=x
2−δ
P
4−δ
(t<T
0
) .
6.2.7 Squared Radial Ornstein-Uhlenbeck
The above attempt to deal with negative dimension has shown a number of
drawbacks. From now on, we shall maintain positive dimensions.
Definition 6.2.7.1 The solution to the SDE
dX
t
=(a − bX
t
)dt +2
|X
t
|dW
t
where a ∈ R
+
,b ∈ R is called a squared radial Ornstein-Uhlenbeck process
with dimension a. We shall denote by
b
Q
a
x
its law, and Q
a
x
=
0
Q
a
x
.
Proposition 6.2.7.2 The following absolute continuity relationship between
a squared radial Ornstein-Uhlenbeck process and a squared Bessel process
holds:
b
Q
a
x
|
F
t
=exp
−
b
4
(X
t
− x − at) −
b
2
8
t
0
X
s
ds
Q
a
x
|
F
t
.
Proof: This is a straightforward application of Girsanov’s theorem. We have
t
0
X
s
dW
s
=
1
2
(X
t
− x − at).
Exercise 6.2.7.3 Let X be a Bessel process with dimension δ<2, starting
at x>0andT
0
=inf{t : X
t
=0}. Using time reversal theorem (see (6.2.8),
prove that the density of T
0
is
1
tΓ (α)
x
2
2t
α
e
−x
2
/(2t)
where α =(4− δ)/2 − 1, i.e., T
0
is a multiple of the reciprocal of a Gamma
variable.
6.3 Cox-Ingersoll-Ross Processes
In the finance literature, the CIR processes have been considered as term
structure models. As we shall show, they are closely connected to squared
Bessel processes, in fact to squared radial OU processes.
