Jeanblanc M., Yor M., Chesney M. Mathematical Methods for Financial Markets
Подождите немного. Документ загружается.


6.1 Definitions and First Properties 337
6.1.3 Path Properties
Proposition 6.1.3.1 Let ρ be a δ-dimensional squared Bessel process. For
δ =0, the point 0 is absorbing (the process remains at 0 as soon as it reaches
it). For 0 <δ<2, the BESQ
δ
is reflected instantaneously.
Proof: In the case δ = 0, the point 0 is reached a.s.. It is obvious that the
point is absorbing. In the case 0 <δ<2, the process ρ is a semi-martingale.
The occupation time formula leads to
t ≥
t
0
1
{ρ
s
>0}
ds =
t
0
1
{ρ
s
>0}
(4ρ
s
)
−1
dρ
s
=
∞
0
(4a)
−1
L
a
t
(ρ)da .
Hence, the local time at 0 is identically equal to 0 (otherwise, the integral on
the right-hand side is not convergent). From the study of the local time and
the fact that L
0−
t
(ρ) = 0, we obtain
L
0
t
(ρ)=2δ
t
0
1
{ρ
s
=0}
ds .
Therefore, the time spent by ρ in 0 has zero Lebesgue measure.
• Bessel process with dimension δ>2: It follows from the properties
of the scale function that: for δ>2, the BESQ
δ
x
will never reach 0 and is
a transient process (ρ
t
goes to infinity as t goes to infinity),
P
x
(R
t
> 0, ∀t>0) = 1,
P
x
(R
t
→∞,t→∞)=1.
• Bessel process with dimension δ =2: The BES
2
x
will never reach 0:
P
x
(R
t
> 0, ∀t>0) = 1,
P
x
(sup
t
R
t
= ∞, inf
t
R
t
=0)=1.
• Bessel process with dimension 0 <δ<2: It follows from the
properties of the scale function that for 0 ≤ δ<2 the process R reaches 0
in finite time and that the point 0 is an entrance boundary (see Definition
5.3.3.1). One has, for a>0, P( R
t
> 0, ∀t>a)=0.
6.1.4 Infinitesimal Generator
Bessel Processes
A Bessel process R with index ν ≥ 0 (i.e., with dimension δ =2(ν +1) ≥ 2) is
a diffusion process which takes values in R
+
and has infinitesimal generator
A =
1
2
d
2
dx
2
+
2ν +1
2x
d
dx
=
1
2
d
2
dx
2
+
δ − 1
2x
d
dx
,
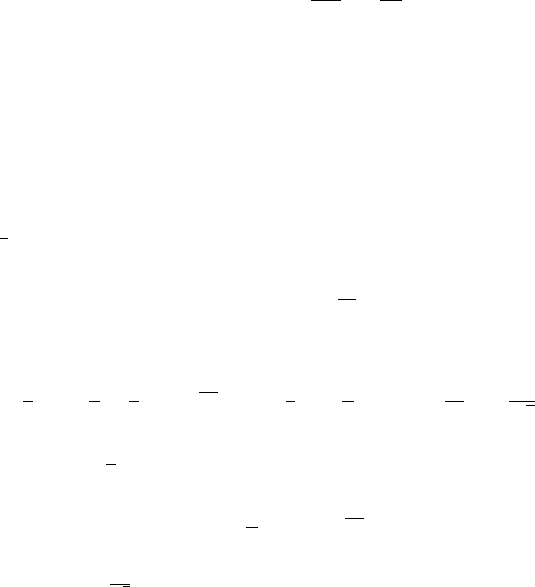
338 6 A Special Family of Diffusions: Bessel Processes
i.e., for any f ∈ C
2
(]0, ∞[), and R
0
= r>0 the process
f(R
t
) −
t
0
Af(R
s
)ds, t ≥ 0
is a local martingale. In particular, if R is a BES
(ν)
, the process 1/(R
t
)
2ν
is
a local martingale. Hence the scale function is s(x)=−x
−2ν
for ν ≥ 0. For
δ>1,aBES
δ
r
satisfies E
r
t
0
ds(R
s
)
−1
< ∞, for every r ≥ 0.
The BES
1
is a reflected Brownian motion R
t
= |β
t
| = W
t
+ L
t
where W
and β are Brownian motions and L is the local time at 0 of Brownian motion β.
Squared Bessel Processes
The infinitesimal generator of the squared Bessel process ρ is
A =2x
d
2
dx
2
+ δ
d
dx
hence, for any f ∈ C
2
(]0, ∞[), the process
f(ρ
t
) −
t
0
Af(ρ
s
)ds
is a local martingale.
Proposition 6.1.4.1 (Scaling Properties.) If (ρ
t
,t≥ 0) is a BESQ
δ
x
, then
(
1
c
ρ
ct
,t≥ 0) is a BESQ
δ
x/c
.
Proof: From
ρ
t
= x +2
t
0
√
ρ
s
dW
s
+ δt,
we deduce that
1
c
ρ
ct
=
x
c
+
2
c
ct
0
√
ρ
s
dW
s
+
δ
c
ct =
x
c
+2
ct
0
ρ
s
c
1/2
1
√
c
dW
s
+ δt .
Setting u
t
=
1
c
ρ
ct
, we obtain using a simple change of variable
u
t
=
x
c
+2
t
0
√
u
s
d
W
s
+ δt
where (
W
t
=
1
√
c
W
tc
,t≥ 0) is a Brownian motion.

6.1 Definitions and First Properties 339
δ =2(1+ν)
δ =2 0 is polar ln R is a strict R is a semi-martingale
local-martingale
δ>2 0 is polar R
−2ν
is a strict R is a semi-martingale
local-martingale
2 >δ>1 R reflects at 0 R
−2ν
is a R is a semi-martingale
sub-martingale
δ =1 R reflects at 0 R is a R is a semi-martingale
sub-martingale
1 >δ>0 R reflects at 0 R
−2ν
is a R is not a semi-martingale
sub-martingale
δ =0 0 is absorbing R
2
is a martingale R is a semi-martingale
Fig. 6.1 Bessel processes
Comment 6.1.4.2 Delbaen and Schachermayer [237] allow general admis-
sible integrands as trading strategies, and prove that the three-dimensional
Bessel process admits arbitrage possibilities. Pal and Protter [692], Yen and
Yor [856] establish pathological behavior of asset price processes modelled by
continuous strict local martingales, in particular the reciprocal of a three-
dimensional Bessel process under a risk-neutral measure.
6.1.5 Absolute Continuity
On the canonical space Ω = C(R
+
, R
+
), we denote by R the canonical map
R
t
(ω)=ω(t), by R
t
= σ(R
s
,s≤ t) the canonical filtration and by P
(ν)
r
(resp.
P
δ
r
) the law of the Bessel process of index ν (resp. of dimension δ), starting at
r, i.e., such that P
(ν)
r
(R
0
= r) = 1. The law of BESQ
δ
starting at x on the
canonical space C(R
+
, R
+
) is denoted by Q
δ
x
.

340 6 A Special Family of Diffusions: Bessel Processes
Proposition 6.1.5.1 The following absolute continuity relation between the
laws of a BES
(ν)
(with ν ≥ 0)andaBES
(0)
holds
P
(ν)
r
|
R
t
=
R
t
r
ν
exp
−
ν
2
2
t
0
ds
R
2
s
P
(0)
r
|
R
t
. (6.1.5)
Proof: Under P
(0)
, the canonical process R which is a Bessel process with
dimension 2, satisfies
dR
t
= dW
t
+
1
2R
t
dt .
Itˆo’s formula applied to the process
D
t
=
R
t
r
ν
exp
−
ν
2
2
t
0
ds
R
2
s
leads to
dD
t
= νD
t
(R
t
)
−1
dW
t
,
therefore, the process D is a local martingale. We prove now that it is a
martingale.
Obviously, sup
t≤T
D
t
≤ sup
t≤T
(R
t
/r)
ν
. The process R
2
is a squared Bessel
process of dimension 2, and is equal in law to B
2
+
˜
B
2
where B and
˜
B are
independent BMs. It follows that R
k
t
is integrable for k ≥ 2. The process R
is a submartingale as a sum of a martingale and an increasing process, and
Doob’s inequality (1.2.1) implies that
E
sup
t≤T
R
t
k
≤ C
k
E[R
k
T
].
Hence, the process D is a martingale. From Girsanov’s theorem, it follows
that the process Z defined by
dZ
t
= dW
t
−
ν
R
t
dt = dR
t
−
1
R
t
ν +
1
2
dt
is a Brownian motion under P
(ν)
r
where P
(ν)
r
|
R
t
= D
t
P
(0)
r
|
R
t
.
If the index ν = −μ is negative (i.e., μ>0), then the absolute continuity
relation holds before T
0
, the first hitting time of 0:
P
(ν)
r
|
R
t
∩{t<T
0
}
=
R
t
r
ν
exp
−
ν
2
2
t
0
ds
R
2
s
P
(0)
r
|
R
t
. (6.1.6)
Comparison with equality (6.1.5) shows that,
for ν<0, P
(−ν)
r
|
R
t
=
R
−2ν
t∧T
0
r
−2ν
P
(ν)
r
|
R
t
.
(6.1.7)

6.1 Definitions and First Properties 341
In particular, this shows that the BES
3
process (μ =1/2) is an h-transform
of Brownian motion killed at 0, which simply means
P
(1/2)
r
|
R
t
=
R
t∧T
0
r
P
(−1/2)
r
|
R
t
or, if W
a
denotes the law of the BM starting from a>0andT
0
the hitting
time of 0,
P
3
a
F
t
=
X
t∧T
0
a
W
a
F
t
. (6.1.8)
(See Dellacherie et al. [241].)
Comment 6.1.5.2 The absolute continuity relationship (6.1.5) has been of
some use in a number of problems, see, e.g., Kendall [518] for the computation
of the shape distribution for triangles, Geman and Yor [383] for the pricing of
Asian options, Hirsch and Song [437] in connection with the flows of Bessel
processes and Werner [839] for the computation of Brownian intersection
exponents.
Exercise 6.1.5.3 With the help of the explicit expression for the semi-group
of BM killed at time T
0
(3.1.9), deduce the semi-group of BES
3
from formula
(6.1.8).
Exercise 6.1.5.4 Let S be the solution of
dS
t
= S
2
t
dW
t
where W is a Brownian motion. Prove that X =1/S is a Bessel process of
dimension 3.
This kind of SDE will be extended to different choices of volatilities in
Section 6.4.
Exercise 6.1.5.5 Let R be a BES
3
process starting from 1. Compute
E(R
−1
t
).
Hint: From the absolute continuity relationship
E(R
−1
t
)=W
1
(T
0
>t)=P(|G| < 1/
√
t)
where G is a standard Gaussian r.v..
Exercise 6.1.5.6 Let R and
R be two independent BES
3
processes. The
process Y
t
= R
−1
t
−(
R
t
)
−1
is a local martingale with null expectation. Prove
that Y is a strict local martingale.
Hint: Let T
n
be a localizing sequence of stopping times for 1/R.IfY were a
martingale, 1/
R
t∧T
n
would also be a martingale. The expectation of 1/
R
t∧T
n
can be computed and depends on t.

342 6 A Special Family of Diffusions: Bessel Processes
Exercise 6.1.5.7 Let R and R be two independent BES
3
processes. Prove
that the filtration generated by the process Y
t
= R
−1
t
−
R
−1
t
is the filtration
generated by the processes R and
R.
Hint: Indeed, the bracket of Y , i.e.,
t
0
(
1
R
4
s
+
1
e
R
4
s
)ds is adapted w.r.t. the
filtration (Y
t
,t≥ 0) generated by Y . Hence the process (
1
R
4
t
+
1
e
R
4
t
)isY-adapted.
Now, if a and b are given, there exists a unique pair (x, y) of positive numbers
such that x − y = a, x
4
+ y
4
= b (this pair can even be given explicitly,
noting that x
4
+ y
4
− (x − y)
4
=2xy(xy − 2(x − y)
2
)). This completes the
proof.
6.2 Properties
6.2.1 Additivity of BESQ’s
An important property, due to Shiga and Watanabe [788], is the additivity
of the BESQ family. Let us denote by P ∗ Q the convolution of P and Q,two
probabilities on C(R
+
, R
+
).
Proposition 6.2.1.1 The sum of two independent squared Bessel processes
with respective dimension δ and δ
, starting respectively from x and x
is a
squared Bessel process with dimension δ + δ
, starting from x + x
:
Q
δ
x
∗ Q
δ
y
= Q
δ+δ
x+y
.
Proof: Let X and Y be two independent BESQ processes starting at x
(resp. at y) and with dimension δ (resp. δ
)andZ = X + Y .Wewantto
show that Z is distributed as Q
δ+δ
x+y
. Note that the result is obvious from the
definition when the dimensions are integers (this is what D. Williams calls the
“Pythagoras” property). In the general case
Z
t
= x + y +(δ + δ
)t +2
t
0
X
s
dB
s
+
Y
s
dB
s
,
where (B,B
) is a two-dimensional Brownian motion. This process satisfies
t
0
1
{Z
s
=0}
ds =0.Let
B be a third Brownian motion independent of (B,B
).
The process W defined as
W
t
=
t
0
1
{Z
s
>0}
√
X
s
dB
s
+
√
Y
s
dB
s
√
Z
s
is a Brownian motion (it is a martingale with increasing process equal to t).
The process Z satisfies
Z
t
= x + y +(δ + δ
)t +2
t
0
Z
s
dW
s
,
and this equation admits a unique solution in law.

6.2 Properties 343
6.2.2 Transition Densities
Bessel and squared Bessel processes are Markov processes and their transition
densities are known. Expectation under Q
δ
x
will be denoted by Q
δ
x
[·]. We also
denote by ρ the canonical process (a squared Bessel process) under the Q
δ
-law.
From Proposition 6.2.1.1, the Laplace transform of ρ
t
satisfies
Q
δ
x
[exp(−λρ
t
)] = Q
1
x
[exp(−λρ
t
)]
Q
1
0
[exp(−λρ
t
)]
δ−1
and since, under Q
1
x
,ther.v.ρ
t
is the square of a Gaussian variable, one gets,
using Exercise 1.1.12.3,
Q
1
x
[exp(−λρ
t
)] =
1
√
1+2λt
exp
−
λx
1+2λt
.
Therefore
Q
δ
x
[exp(−λρ
t
)] =
1
(1 + 2λt)
δ/2
exp
−
λx
1+2λt
.
(6.2.1)
Inverting the Laplace transform yields the transition density q
(ν)
t
of a BESQ
(ν)
for ν>−1as
q
(ν)
t
(x, y)=
1
2t
y
x
ν/2
exp
−
x + y
2t
I
ν
(
√
xy
t
) ,
(6.2.2)
and the Bessel process of index ν has a transition density p
(ν)
t
defined by
p
(ν)
t
(x, y)=
y
t
y
x
ν
exp
−
x
2
+ y
2
2t
I
ν
xy
t
(6.2.3)
where I
ν
is the usual modified Bessel function with index ν.(See
Appendix A.5.2 for the definition of modified Bessel functions.) For x =0,
the transition probability of the BESQ
(ν)
(resp. of the BES
(ν)
)is
q
(ν)
t
(0,y)=(2t)
−(ν+1)
[Γ (ν +1)]
−1
y
ν
exp
−
y
2t
,
p
(ν)
t
(0,y)=2
−ν
t
−(ν+1)
[Γ (ν +1)]
−1
y
2ν+1
exp
−
y
2
2t
. (6.2.4)
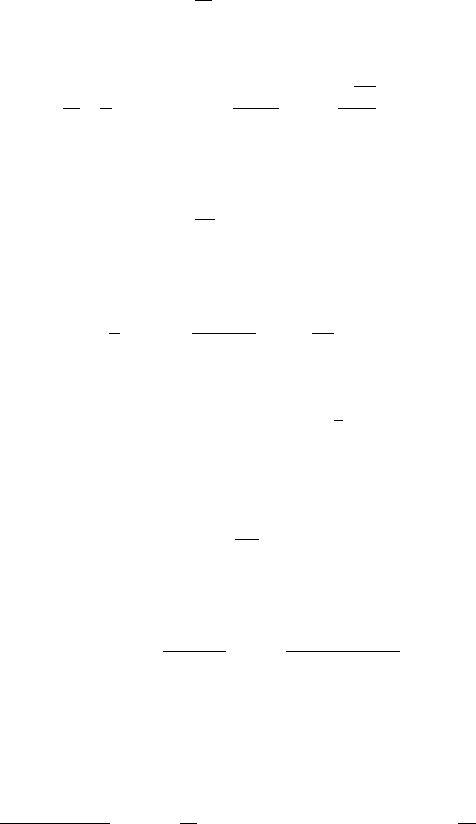
344 6 A Special Family of Diffusions: Bessel Processes
In the case δ = 0 (i.e., ν = −1), the semi-group of BESQ
0
is
Q
0
t
(x, ·) = exp
−
x
2t
0
+
Q
t
(x, ·)
where
0
is the Dirac measure at 0 and
Q
t
(x, dy) has density
q
0
t
(x, y)=
1
2t
y
x
−1/2
exp
−
x + y
2t
I
1
√
xy
t
,
while the semi-group for BES
0
is
P
0
t
(x, ·) = exp
−
x
2
2t
0
+
P
t
(x, ·)
where
P
t
(x, dy) has density
p
0
t
(x, y)=
x
t
exp
−
x
2
+ y
2
2t
I
1
xy
t
.
Remark 6.2.2.1 From the equality (6.2.3), we can check that, if R is a BES
δ
starting from x,thenR
2
t
law
= tZ where Z has a χ
2
(δ,
x
t
)law.(SeeExercise
1.1.12.5 for the definition of χ
2
.)
Comment 6.2.2.2 Carmona [140] presents an extension of squared Bessel
processes with time varying dimension δ(t), as the solution of
dX
t
= δ(t)dt +2
X
t
dW
t
.
Here, δ is a function with positive values. The Laplace transform of X
t
is
E
x
(exp(−λX
t
)) = exp
−λ
x
1+2λt
−
t
0
λδ(u)
1+2λ(t − u)
du
.
See Shirakawa [790] for applications to interest rate models.
Comment 6.2.2.3 The negative moments of a squared Bessel process have
been computed in Yor [863], Aquilina and Rogers [22] and Dufresne [279]
Q
(ν)
x
(ρ
−a
t
)=
Γ (ν +1− a)
Γ (ν +1)
exp
−
x
2t
(2t)
−a
M
ν +1− a, ν +1,
x
2t
where M is the Kummer function given in Appendix A.5.6.
Exercise 6.2.2.4 Let ρ be a 0-dimensional squared Bessel process starting
at x,andT
0
its first hitting time of 0. Prove that 1/T
0
follows the exponential
law with parameter x/2.
Hint: Deduce the probability that T
0
≤ t from knowledge of Q
0
x
(e
−λρ
t
).
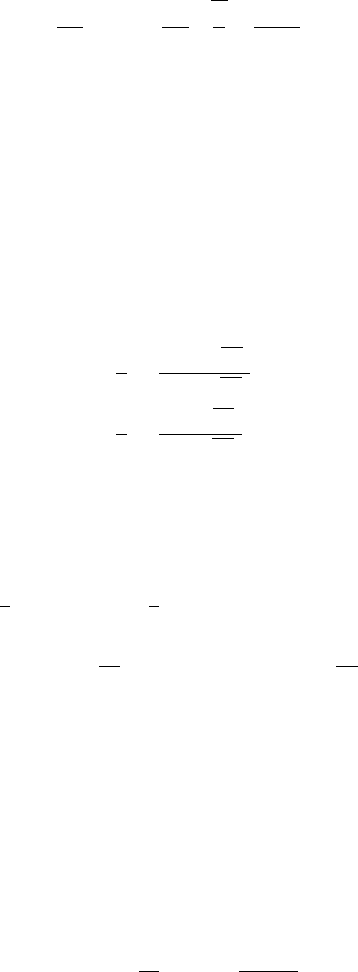
6.2 Properties 345
Exercise 6.2.2.5 (from Az´ema and Yor [38].) Let X be a BES
3
starting from
0. Prove that 1/X is a local martingale, but not a martingale. Establish that,
for u<1,
E
1
X
1
|R
u
=
1
X
u
2
π
Φ(
X
u
1 − u
) ,
where Φ(a)=
a
0
dy e
−y
2
/2
. Such a formula “ measures” the non-martingale
property of the local martingale (1/X
t
,t ≤ 1). In general, the quantity
E(Y
t
|F
s
)/Y
s
for s<t,orevenitsmeanE(Y
t
/Y
s
), could be considered as
a measure of the non-martingale property of Y .
6.2.3 Hitting Times for Bessel Processes
Expectation under P
(ν)
a
will be denoted by P
(ν)
a
(·). We assume here that ν>0,
i.e., δ>2.
Proposition 6.2.3.1 Let a, b be positive numbers and λ>0.
P
(ν)
a
(e
−λT
b
)=
b
a
ν
K
ν
(a
√
2λ)
K
ν
(b
√
2λ)
, for b ≤ a, (6.2.5)
P
(ν)
a
(e
−λT
b
)=
b
a
ν
I
ν
(a
√
2λ)
I
ν
(b
√
2λ)
, for a ≤ b, (6.2.6)
where K
ν
and I
ν
are modified Bessel functions, defined in Appendix A.5.2.
Proof: The proof is an application of (5.3.8)(seeKent[519]). Indeed, for a
Bessel process the solutions of the Sturm-Liouville equation
1
2
xu
(x)+
ν +
1
2
u
(x) − λxu(x)=0
are
Φ
λ↑
(r)=c
1
I
ν
(r
√
2λ)r
−ν
,Φ
λ↓
(r)=c
2
K
ν
(r
√
2λ)r
−ν
where c
1
,c
2
are two constants.
Note that, for a>b, using the asymptotic of K
ν
(x), when x →∞,we
may deduce from (6.2.5)thatP
(ν)
a
(T
b
< ∞)=(b/a)
2ν
. Another proof may be
given using the fact that the process M
t
=(1/R
t
)
δ−2
is a local martingale,
which converges to 0, and the result follows from Lemma 1.2.3.10.
Here is another consequence of Proposition 6.2.3.1, in particular of formula
(6.2.5): for a three-dimensional Bessel process (ν =1/2) starting from 0, from
equality (A.5.3) in Appendix which gives the value of the Bessel function of
index 1/2,
P
3
0
exp
−
λ
2
2
T
b
=
λb
sinh λb
.

346 6 A Special Family of Diffusions: Bessel Processes
For a three-dimensional Bessel process starting from a
P
3
a
exp
−
λ
2
2
T
b
=
b
a
sinh λa
sinh λb
, for b ≥ a, (6.2.7)
P
3
a
exp
−
λ
2
2
T
b
=
b
a
exp (−(a − b)λ) , for b<a.
Inverting the Laplace transform, we obtain the density of T
b
, the hitting time
of b for a three-dimensional Bessel process starting from 0:
P
3
0
(T
b
∈ dt)=
n≥1
(−1)
n+1
π
2
n
2
b
2
e
−n
2
π
2
t/(2b
2
)
dt .
For b<a, it is simple to find the density of the hitting time T
b
for a BES
3
a
.
The absolute continuity relationship (6.1.8) yields the equality
E
3
a
(φ(T
b
)) =
1
a
W
a
(φ(T
b
)X
T
b
∧T
0
)
which holds for b<a. Consequently
P
3
a
(T
b
>t)=P
3
a
(∞ >T
b
>t)+P
3
a
(T
b
= ∞)=
b
a
W
0
(T
a−b
>t)+1−
b
a
=
b
a
P(a − b>
√
t|G|)+1−
b
a
.
where G stands for a standard Gaussian r.v. under P. Hence
P
3
a
(T
b
>t)=
b
a
2
π
(a−b)/
√
t
0
e
−y
2
/2
dy +1−
b
a
.
Note that P
3
a
(T
b
< ∞)=
b
a
. The density of T
b
is
P
3
a
(T
b
∈ dt)/dt =(a − b)
1
√
2πt
3
b
a
exp
−
(a − b)
2
2t
.
Thanks to results on time reversal (see Williams [840], Pitman and Yor
[715]) we have, for R a transient Bessel process starting at 0, with dimension
δ>2 and index ν>0, denoting by Λ
1
the last passage time at 1,
(R
t
,t<Λ
1
)
law
=(
R
T
0
−u
,u≤ T
0
(
R)) (6.2.8)
where
R is a Bessel process, starting from 1, with dimension
δ =2(1−ν) < 2.
Using results on last passage times (see Example 5.6.2.3), it follows that
T
0
(
R)
law
=
1
2γ(ν)
(6.2.9)
where γ(ν) has a gamma law with parameter ν.
Comment 6.2.3.2 See Pitman and Yor [716] and Biane et al. [86]formore
comments on the laws of Bessel hitting times. In the case a<b, the density
of T
b
under P
3
a
is given as a series expansion in Ismail and Kelker [460]and
Borodin and Salminen [109]. This may be obtained from (6.2.7).
