Jan Svoboda. Magnetic Techniques for the Treatment of Materials
Подождите немного. Документ загружается.

370 CHAPTER 5. PRACTICAL ASPECTS OF MAGNETIC METHODS
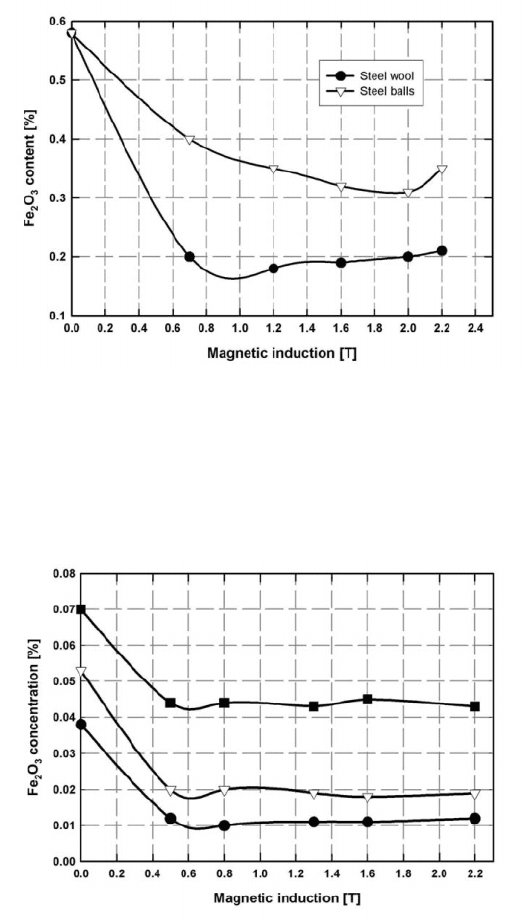
Figure 5.37: The eect of the magnetic induction on the concentration of iron
oxide in kaolin (South Africa) (adapted from [S32]).
Figure 5.38: The eect of the magnetic induction on the concentration of iron
oxide in three glass sand materials (adapted from [S32]).

5.3. WET MAGNETIC SEPARATION 371
Figure 5.39: The eect of the magnetic induction on the brightness of the Geor-
gia kaolin, for dierent values of feed velocity. Matrix length: 500
mm, matrix loading: 3.7 bed volumes (adapted from [S60]).
increasing magnetic field, the brightness of the Georgia kaolin clay improved
[S60].
In addition to the conflict between grade and recovery, there are valid eco-
nomic constraints on the selection of the magnetic field strength. In the design
of magnetic separation systems, the capital investment and processing costs
increase rapidly as magnetic induction is increased. It is, therefore, desirable
to use the lowest practical magnetic field strength consistent with acceptable
product quality.
The concentration of minerals The selection of the operating magnetic
field in the concentration of weakly magnetic minerals is a sensitive task and
only a well defined objective of separation will determine the approach taken.
The traditional conception is that an increase in the magnetic field strength will
result in an increase in recovery of weakly magnetic materials. Recovery of iron
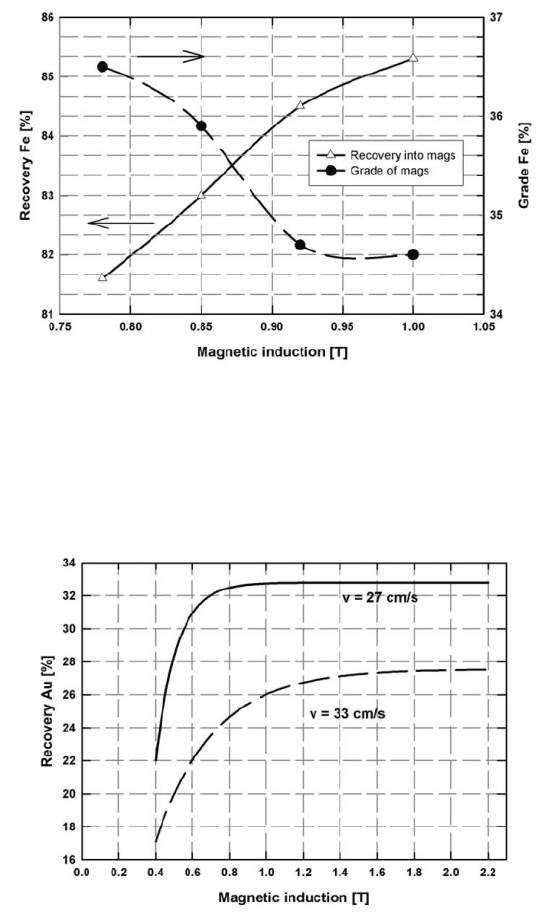
from feebly magnetic Anshan (China) iron ore, illustrated in Fig. 5.40 exhibits
such a trend.
There are, however, certain factors, already discussed, that can cause the re-
covery into the magnetic product to decrease with increasing magnetic field, and
there is usually an optimum magnetic field strength at which recovery reaches
its maximum. With further increase in the field, recovery either remains con-
stant or even decreases. Such trends are illustrated by the beneficiation of gold
ore flotation tailings (Fig. 5.41) and manganese ore (Fig. 5.42).
Moreover, in contrast to magnetic filtration, or to many applications of the
372 CHAPTER 5. PRACTICAL ASPECTS OF MAGNETIC METHODS
Figure 5.40: Beneficiation of the Anshan (China) iron ore by SLON HGMS
(adapted from Xiong [X2]).
Figure 5.41: Recovery of gold by HGMS from East Rand (South Africa) flotation
tailings (- 75 m), as a function of the magnetic field, for two values
of flow velocity (adapted from [S32]).

5.3. WET MAGNETIC SEPARATION 373
Figure 5.42: Recovery of Fe and Mn from manganese ore (South Africa, - 75
m) by HGMS (adapted from [S32]).
Figure 5.43: The grade of the magnetic concentrate from HGMS of gold flotation
tailings (South Africa), as a function of magnetic induction, for
three size fractions (adapted from [S32]).
374 CHAPTER 5. PRACTICAL ASPECTS OF MAGNETIC METHODS
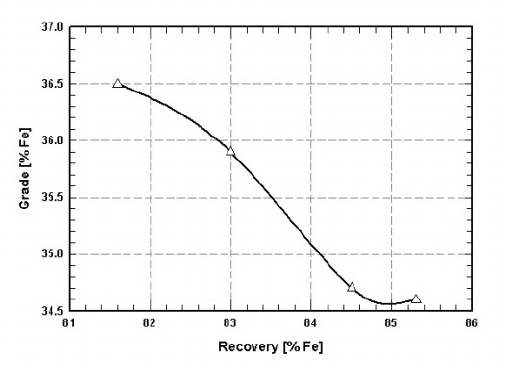
Figure 5.44: A typical relationship between the recovery of iron into the mag-
netic concentrate and the grade of the magnetics (based on Fig.
5.40).
removal of magnetic impurities from industrial minerals, the recovery of a valu-
able component is not the only criterion of the performance of a magnetic separa-
tor when applied to concentration. The grade of the magnetic product is usually
equally important and the magnetic field strength has, therefore, to be selected
in such a way that recovery and grade are optimized simultaneously. The grade
of the magnetic concentrate usually decreases with increasing magnetic field, as
a consequence of non-selective magnetic capture caused by the entrainment of
non-magnetic gangue particles in clusters of magnetizable particles, and by the
capture of non-liberated grains containing magnetic inclusions.
A decrease in the grade of the magnetic concentrate with increasing magnetic
field represents a characteristic feature of a majority of magnetic separation
applications to mineral concentration. Figures 5.40 and 5.43 illustrate this trend
in the beneficiation of iron ore and gold ore flotation tailings respectively.
Clearly, a selection of the applied magnetic field strength must be based on
an evaluation of the interplay between recovery and grade of the concentrate,
and on the relative importance ascribed to these two metallurgical factors. The
importance of the trade-o between the recovery and the grade is depicted in
Fig. 5.44.
It has been shown, therefore, that a higher magnetic field does not necessarily
mean better results. The optimum magnetic field has to be determined in each
particular case in such a manner that the recovery-grade relationship satisfies
the objectives of the application.
5.3. WET MAGNETIC SEPARATION 375
5.3.4 Matrix in high-gradient magnetic separators
The importance of a correct choice of matrix for magnetic filtration and material
concentration cannot be overemphasized. The shape and size of the matrix play
a decisive role in the achievement of optimum recovery and concentrate grade,
and determine matrix loading.
In spite of the importance of a correct choice of matrix, little attention has
been paid to the theoretical analysis of the optimum matrix size and geometry.
The attention was mainly concentrated on maximizing the magnetic force in a
single-collector approach, with the aim of applying these rules to multi-collector
matrix.
The magnetic force has been shown to reach a maximum for the ratio of the
collector radius d to particle radius e equal to approximately three [O5, A29].
Further theoretical [M27] and experimental investigations have indicated that
the optimum ratio d@e is a function of a variety of parameters, such as magnetic
induction, particle size, type of matrix and matrix loading [S1].
Although the conclusions of the single-collector-single-particle studies are
useful for a better understanding of the dynamics of a magnetizable particle in
the vicinity of an isolated magnetized collector, their validity for a real matrix
is very limited.
Straining and mechanical capture
Attempts to maximize the ratio of traction magnetic force to hydrodynamic
drag usually result in particle capture by a straining mechanism. If d@e ? 10,
mechanical straining is dominant and leads to the formation of a surface mat
of deposit on the matrix. This layer of deposit causes high resistance to the
flow, and increases entrainment of non-magnetic particles in the deposit. This
phenomenon is detrimental to the e!ciency of separation, irrespective of the
type of application. It either increases losses of the non-magnetic concentrate
or impairs the grade of the magnetic concentrate.
Therefore, straining should be avoided in the design of magnetic separators.
For straining to be minimized, d@e should be larger than 10, but preferably
should range from 100 to 500. However, even for high values of d@e, a certain
fraction of particles fed into the separator will be mechanically captured. As
a rule, mechanical entrapment increases both for coarse particles and for finer
matrices.
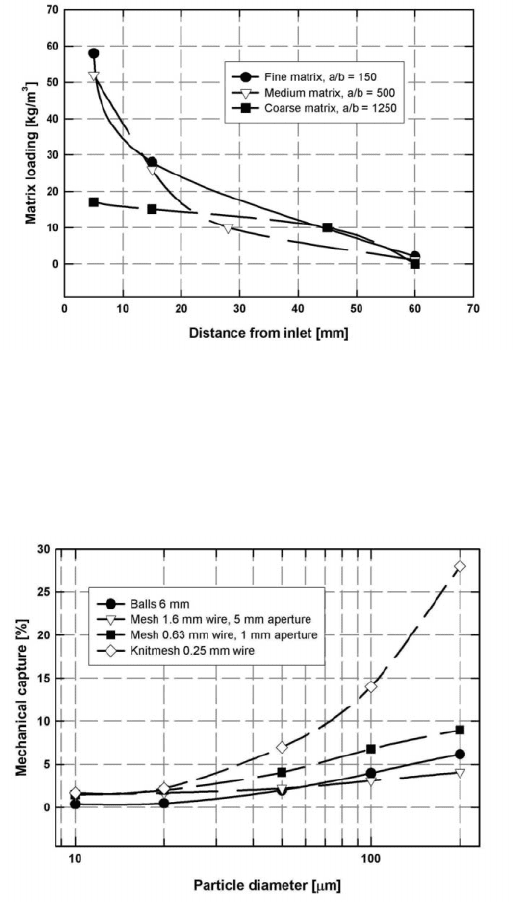
The presence of straining for fine matrices is demonstrated in Fig. 5.45. It
can be seen that straining is absent and particles are deposited almost uniformly
throughout the filter for a coarse matrix with d@e = 1250, while with finer
matrices, particles are predominantly deposited in the vicinity of the filter inlet
[E4].
In addition to straining, some particles are retained by the matrix even in
the absence of the external magnetic field, as follows from the deep bed model of
magnetic separation [S31, S33] discussed in Section 3.4.2. Figures 5.46 and 5.47
illustrate that, for a given type of matrix, mechanical retention increases with
376 CHAPTER 5. PRACTICAL ASPECTS OF MAGNETIC METHODS
Figure 5.45: Matrix loading as a function of distance from the inlet into a mag-
netic filter, for three types of matrices (adapted from [E4]).
Figure 5.46: Mechanical capture of uraninite particles, as a function of particle
size, for various types of matrices, at the superficial velocity of 0.02
m/s (adapted from [S61]).

5.3. WET MAGNETIC SEPARATION 377
Figure 5.47: Mechanical capture, as a function of the diameter of the matrix
element, of various size fractions of uraninite particles, at a flow
velocity of 0.02 m/s (adapted from [S61]).
increasing particle size. In addition, it can be seen that mechanical capture
increases with increasing fineness of the matrix. Also in agreement with the
concept of deep bed filtration, the particle retention decreases with increasing
flow velocity of the slurry through the matrix, as depicted in Fig. 5.48.
The optimum size of a matrix
In the application of HGMS to the beneficiation of minerals, the matrix should
be matched to the feed properties in such a way that recovery and grade are at
their maximum simultaneously. The optimum collector size becomes, therefore,
a function of the size distribution of the ore, and of the hydrodynamic conditions
in the inter-matrix space. The usual practice is a trial-and-error search for the
best size and shape of the matrix.
During this process, several fundamental rules should be kept in mind. With
a decreasing collector diameter, the recovery into the magnetic fraction usually
increases, whereas the grade of the concentrate decreases. With very fine matri-
ces, the mass yield into the magnetic concentrate becomes high and the grades
too low.
Numerous experimental results show that the most satisfactory metallurgi-
cal performance is obtained with the ratio of the collector size to particle size
ranging from 100 to 300. This is demonstrated in Fig. 5.49, in which the grade
of the magnetic concentrate is plotted as a function of the diameter of the ma-
trix elements. It can be seen that, for fine matrices, the grade is very low, higher
grades being obtained for fairly coarse matrices, for which d@e is about 350. For
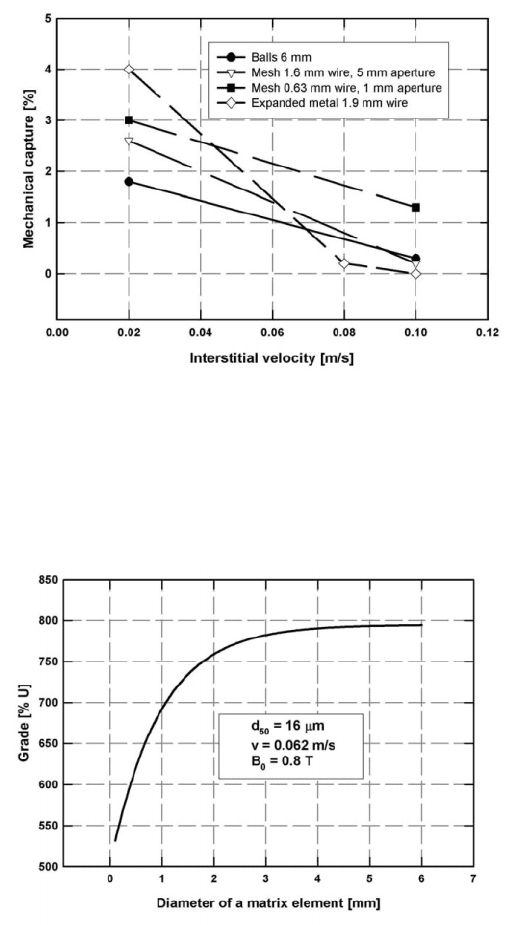
378 CHAPTER 5. PRACTICAL ASPECTS OF MAGNETIC METHODS
Figure 5.48: Mechanical entrapment, in assorted matrices, of uraninite particles
(- 176 m), as a function of flow velocity (adapted from [S61]).
Figure 5.49: The grade of the magnetic uranium concentrate, as a function of
the diameter of matrix elements (adapted from [S61]).
5.3. WET MAGNETIC SEPARATION 379
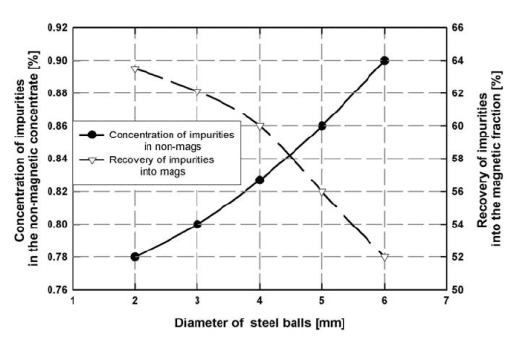
Figure 5.50: The eect of the ball diameter on the e!ciency of kaolin purification
(the Ukraine). E
0
= 1 T, particle size: - 100 m (adapted from
[S62]).
these coarse matrices, the recovery is also su!ciently high.
Similar conclusions may be drawn from Fig. 5.50, which illustrates the eect
of the diameter of steel balls on the e!ciency of kaolin purification [S62]. For
the optimum operation of the separator, the ball diameter is 2 mm to 3 mm,
with d@e being approximately 200 to 300.
Several types of production-scale high-gradient separators, such as VMS-
100 and SLON, have been using successfully rod matrices. The e!ciency of
separation is a function of the rod diameter as illustrated in Fig. 5.51. Equally
e!cient performance of the rod matrix, when applied to beneficiation of fine
ilmenite, was reported by Xiong [X3] and the results are summarized in Fig.
5.52.
One of the most widely used matrix magnetic separators is the Jones sepa-
rator. Vertically arranged grooved plates are used as a matrix, as is shown in
Fig. 2.37. The pattern and the magnitude of the magnetic field gradient can be
modified by using dierent types of plates and by altering the gap between the
plates. Three dierent types of plates, with varying tip radii are available and
their specifications are given in Table 5.22.
Although grooved plates performed successfully on numerous su!ciently
magnetic and coarse ores, their e!ciency to concentrate finely ground refractory
iron ores has often been found unsatisfactory. The width of the gaps between
the plate has frequently been too large to ensure su!cient recovery of weakly
magnetic fine particles. At the same time, a decrease in the width of the gap
caused rapid clogging of the matrix and deterioration in the performance of the
separator.
In order to address this problem, Mekhanobrchermet Institute (the Ukraine)
