James I.N. Introduction to Circulating Atmospheres

Подождите немного. Документ загружается.

1.7

The

quasi-geostrophic approximation

where

/? =

O(f/a). More precisely,

(1.60)

This '/?

-plane'

approximation

very useful

for our

purposes, since

it rep-

resents

the

most important effects

of the

Earth's curvature without having

to write

the

equations

spherical coordinates,

cumbersome procedure

best.

The

ratio

of the two

horizontal advection terms

therefore:

(1.61,

U '

For

the

Earth's midlatitudes, /1L

roughly unity. Both

the

horizontal

advection terms must therefore

retained.

Friction

can

generally

ignored away from

the

Earth's surface,

but may

be large

in the

boundary layer. We will retain

the

friction term

in a

schematic

way

writing

it in

terms

of a

Rayleigh friction.

The

drag timescale x

may

in general

be a

complicated function

of the

flow

and

temperature fields.

Finally,

obtain

quasi-geostrophic form

of the

vorticity equation:

In fact, this equation involves only

two

variables. From

Eq.

(1.52,

the geo-

strophic velocities

can be

written

terms

of a

'geostrophic streamfunction'

so that

Un — T-S Va —

-T-

(1*64)

The vorticity equation involves

the

geostrophic stream function

and the

vertical velocity only.

For some purposes,

will

use the

momentum equations

in a

form which

is consistent with

the

quasi-geostrophic approximation.

It can be

verified

differentiation that

the

pair:

(1.65a)

-ft

-fo

a-PyUg> (1.65b)

The

governing physical laws

lead to the quasi-geostrophic vorticity equation. The vector \

the 'ageostrophic velocity':

—

, (1.66)

which, since the geostrophic velocity is purely rotational, is related directly

to the vertical velocity from the continuity equation, Eq. (1.35):

It follows that the ageostrophic velocity components have magnitude O{Ro)

U. Note that there are no vertical advection terms in Eqs. (1.65a, b).

To obtain a complete and consistent equation set, it is necessary to ap-

proximate the thermodynamic equation also. But first note that the potential

temperature can be written in terms of the geostrophic streamfunction. From

the hydrostatic relation, Eq. (1.32), the definition of potential temperature,

Eq. (1.9), and using Eq. (1.54), we find:

The thermodynamic equation is simplified by writing the potential temperat-

ure as the sum of a standard reference potential temperature which depends

only upon pressure and a departure from this reference atmosphere:

e = 6

(p) + 6

(x,y,p,t). (1.69)

The reference profile 9

may be taken to be the global mean potential tem-

perature at pressure p. The stable stratification of the atmosphere means that

decreases markedly with pressure. The quasi-geostrophic approximation

of the thermodynamic equation involves the assumption that

(1.70)

so that only the vertical advection of the reference potential temperature

is retained. The quasi-geostrophic form of the thermodynamic equation is

therefore:

+ff

._^

. ,1.7!)

Since d6

/dp is always negative for a stably stratified atmosphere, we will

introduce a (positive) stratification parameter which can be related to the

Brunt-Vaisala frequency N:

2 =

-h(p)?pt.

(1.72)

1.8

Potential vorticity

and the

omega equation

The assumption that vertical advection of 9

is negligible is certainly the

weakest tenet of quasi-geostrophic theory. In fact, the stratification of the

atmosphere at a given pressure varies substantially across the globe, and can

fluctuate appreciably even within individual weather systems. Nevertheless,

quasi-geostrophic theory provides a helpful basis for understanding many

aspects of the global circulation, and for the diagnosis of dynamical processes

from observations or model output. It will be used repeatedly in later

chapters.

Eqs.

(1.62) and (1.71) involve just two unknown dependent variables.

These are the geostrophic streamfunction and the vertical velocity. The

quasi-geostrophic equations therefore constitute a complete set of equations

for the motion of the atmosphere, although of course, they will become

invalid near the equator.

1.8

Potential vorticity

and the

omega equation

It is straightforward to eliminate the vertical velocity between Eqs. (1.62)

and (1.71), obtaining a single prognostic equation for the geostrophic stream

function. Differentiating Eq. (1.71) with respect to p and eliminating dco/dp

between the thermodynamic and vorticity equations gives:

where the operator D

/Dt indicates a rate of change following the geo-

strophic wind. More compactly, Eq. (1.73) can be written:

.74)

where

{ £(gg)}

a.75,

is the 'quasi-geostrophic potential vorticity'. Note that this is conserved

following the geostrophic wind if friction and heating can be neglected.

Furthermore, Eq. (1.75) may be regarded as an elliptic equation relating the

geostrophic streamfunction to the potential vorticity. If the distribution of

potential vorticity is known, and boundary conditions on

are specified,

then, in principle, Eq. (1.75) can be inverted to yield v

and 9 everywhere.

22 The governing physical laws

An alternative is to eliminate the time derivatives between Eqs (1.62) and

(1.71).

When this is done, one obtains an elliptic diagnostic equation for the

vertical velocity:

v2{WJ) a76)

Eq. (1.76) is frequently called the 'omega equation'. Again, this equation may

be inverted, given suitable boundary conditions on co, so that the vertical

velocity can be deduced from the geostrophic streamfunction. If the 'source

terms'

on the right hand side are positive, then

will tend to be negative,

that is, there will be ascent. Conversely, descent will be associated with a

minimum of the source terms. The right hand side of Eq. (1.76) consists

of two terms. The first includes the vertical gradient of the advection of

absolute vorticity, together with the vorticity tendency due to friction. The

second includes the Laplacian of the advection of potential temperature, and

the heating term. In many common meteorological situations, the friction

and heating terms are small compared to the advection terms; the advection

terms tend to cancel out, and so a qualitative determination of the vertical

velocity field can be difficult.

Finally, it may be noted that an alternative formulation of the right hand

side of the omega equation exists which avoids problems of cancellation. It

is written as the divergence of a vector Q where:

•

Q (1.77)

where

d\o d6

(\ IQ\

Here, s denotes a coordinate parallel to the local 6 contour, and n is a

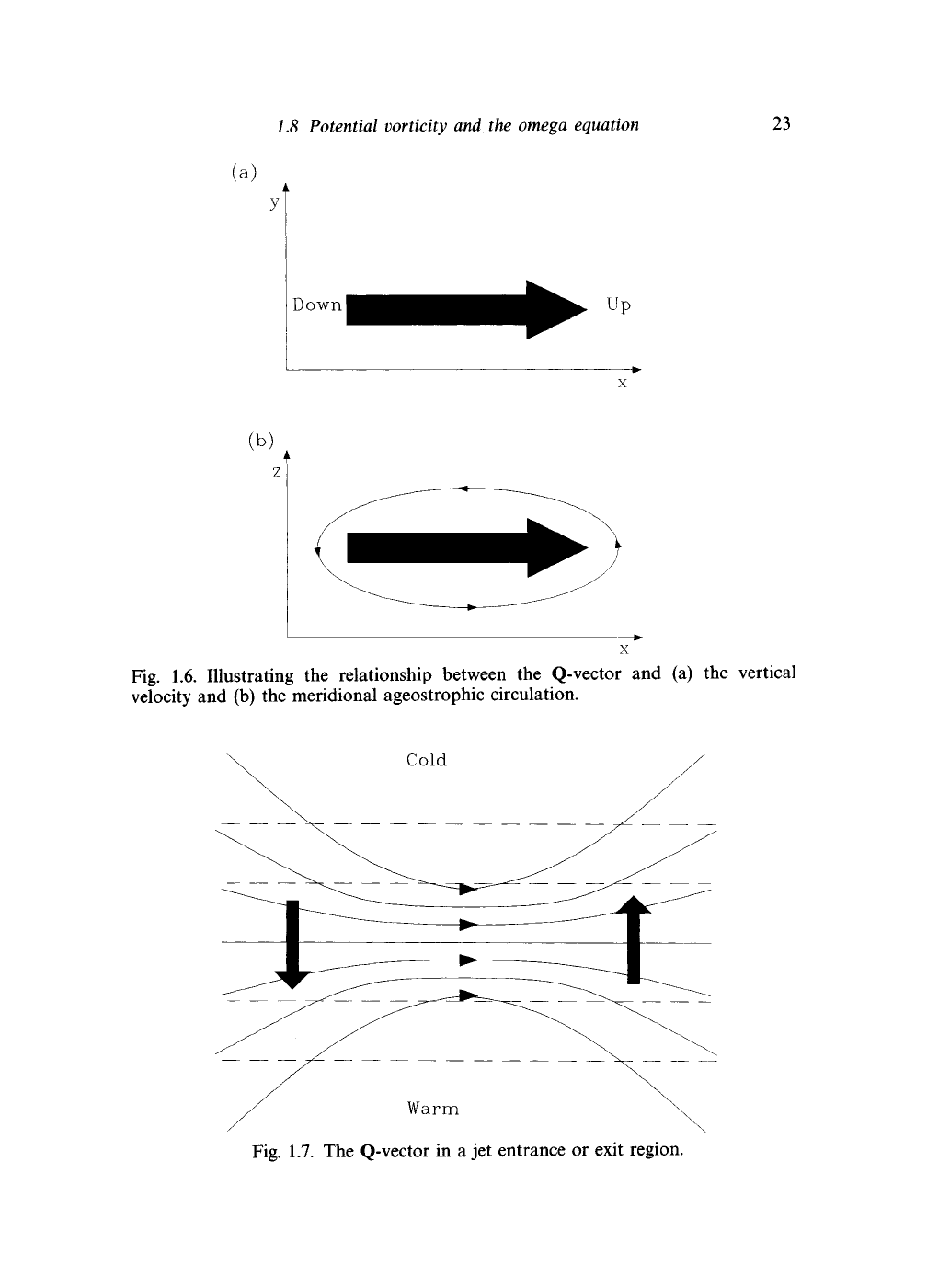
coordinate at right angles to the 6 contour. The Q-vectors converge on to

regions of ascent and diverge from regions of descent. In the vertical plane,

continuity implies that there is an anticlockwise ageostrophic circulation

around the Q-vector. Figure 1.6 illustrates the relationship between Q and

the ageostrophic circulation. In a localized region, across which variations

of / can be neglected, a simple recipe can be deduced for determining

the direction of the Q-vector. The recipe is: take the vector change of the

wind along a 9 contour (moving with cold air on the left) and rotate the

vector clockwise through 90°. Figure 1.7 illustrates the method for a jet exit

region.

To summarize, and to provide a handy reference for later chapters,

1.8 Potential vorticity and the omega equation

(a)

Down

(b)

Fig. 1.6. Illustrating the relationship between the Q-vector and (a) the vertical

velocity and (b) the meridional ageostrophic circulation.

Cold

/ Warm

Fig. 1.7. The Q-vector in a jet entrance or exit region.

The

governing physical laws

Table 1.3 draws together the complete set of quasi-gesotrophic equations,

together with the definitions of the notation used.

1.9

ErtePs potential vorticity

The quasi-geostrophic potential vorticity cannot be applied near the equator

where the geostrophic approximation breaks down, nor is it valid to apply it

in regions where the static stability changes sharply on a pressure surface. A

more general potential vorticity can be defined which avoids this problem.

Sometimes called 'Ertel's potential vorticity', it is defined as

,,_P«i±O.

. (1.79)

If friction and heating are negligible, then q

is conserved following the full

three-dimensional motion, that is,

^+u-Vq

=0.

(1.80)

As in the case of the quasi-geostrophic potential vorticity, the distribution

of q

can be 'inverted' to yield both the velocity field and the potential

temperature field. This requires two conditions to be met. First, suitable

boundary conditions must be specified. Second, there must be a 'balance

condition' relating the temperature and velocity fields to each other. Thermal

wind balance is the simplest such condition.

A physical interpretation of the Ertel potential vorticity is shown in

Fig.

1.8. If the 9 surfaces move apart, then conservation of 9 means that a

column of fluid between these surfaces must remain bounded by them and

so must stretch. Conservation of angular momentum (friction is presumed

zero),

then, means that the relative vorticity must become more cyclonic.

Conversely, if the 9 surfaces move together, the column must become more

anticyclonic.

Scale analysis shows that q

is dominated by the contribution of the

vertical terms, so that to a good approximation:

(An equivalent expression in pressure coordinates may be preferred.) It is

this dominance of the vertical contribution to the Ertel potential vorticity

which justifies ignoring the horizontal components of the vorticity equation

in Section 1.6. The quasi-geostrophic potential vorticity can be recovered

from this relationship. First, note that | / |» | £ | for geostrophic conditions.

1.9 Ertel's potential vorticity 25

Table

1.3. A summary of

quasi-geostrophic

relationships and definitions.

Geostrophic streamfunction:

V>g

= ^j- (1-61)

Geostrophic winds:

(1.52a)

(1.52b)

J ex

Thermal wind relationships:

= -

gdZ_

>_d_Z_

hd6

fSy

^—^

(1.53)

where

h(p)

-[-)

(1.54)

Thermodynamic equation:

where

=-%)—A (1.72)

Vorticity equation:

Momentum equations:

-± (1.65a)

Potential vorticity equation:

Omega equation:

co + — —^ = — — i v

•

V<^

+ pv 4- — i

•

—

^} (1-76)

Definition of

Q-vector:

Q = kx^|^ (1.78)

The governing physical laws

Isentrope

Fig. 1.8. Ertel's potential vorticity.

Second, divide 9 into a reference profile and a small anomaly. Then,

multiplying out the terms in Eq. (1.81) and dropping the products of small

terms,

the quasi-geostrophic potential vorticity can be recovered.

The Ertel potential vorticity combines the dynamics and thermodynamics

of the atmosphere into a single equation. It is the most compact, and argu-

ably the most fundamental description of the atmospheric flow. An ideal

goal is to describe the global circulation entirely in terms of the sources,

sinks and transports of potential vorticity. This is a goal which has not

yet been attained, not least because accurate observations of q

have only

recently become available. There are also conceptual difficulties. There is

every reason to suppose that the structure of the potential vorticity field

contains large fluctuations on the smallest scales that one cares to resolve.

Modelling studies show that initially smooth distributions of q

rapidly

develop extremely fine structure. Implicit in any description of the global

circulation of q

is some sort of large scale smoothing; whether a rational

basis for such smoothing exists has yet to be demonstrated.

1.10 Problems

1.1 Deduce an expression relating the mass mixing ratio of atmospheric

constituents to their volume mixing ratio, and hence translate Table 1.1 into

mass mixing ratios.

1.2 A parcel of air, temperature

°C,

is lifted slowly from the Earth's

surface to a height of

km, such that it remains in thermodynamic equi-

librium with its surroundings. Assuming that the Brunt-Vaisala frequency

1.10 Problems 27

N = ^/g/6)d6/dz is a constant, equal to 10

s *, calculate the amount of

heat gained or lost by the parcel.

1.3 A parcel of fluid at latitude 0 on a rotating planet is observed moving

at a speed U. If only the Coriolis force acts upon it, show that it moves in a

circular trajectory, and calculate the time taken to execute each circle.

1.4 Use the hydrostatic relation to derive a correction of the observed

surface pressure to obtain mean sea level pressure, assuming that the lower

atmosphere has a constant lapse rate F. A station situated

150

m above mean

sea level observes a pressure of 98.5 kPa, a temperature of 15 °C. Assuming

a lapse rate of 6Kkm~~

, estimate the mean sea level pressure. What error

would be made in the mean sea level pressure correction if the atmosphere

was assumed to be isothermal?

1.5 Starting from Eqs. (1.65a,b), deduce the ageostrophic wind in a steady

jet exit, in which the 25kPa wind decreases from

ms"

to 25 ms"

over

a distance of 1500 km at a latitude of 40 °N. Estimate the strength of the

vertical velocities in the jet exit assuming the jet width is 1000 km.

1.6 Show that the quasi-geostrophic potential vorticity, using height as a

vertical coordinate, may be written:

Show that under suitable conditions, Ertel's potential vorticity is propor-

tional to this expression, and deduce the constant of proportionality.

Observing

and

modelling global circulations

2.1 Averaging

the

atmosphere

Strictly speaking, describing global atmospheric circulations requires the

specification of the evolving three-dimensional fields of meteorological vari-

ables. Such a data compilation would be indigestible, and our description

of the global circulation generally implies that some kind of averaging has

been carried out. The flow is thought of as consisting of a 'mean' part, and

a fluctuating or 'eddy' part. It is assumed that the details of any individual

eddies are unimportant, though the average properties of eddies may well

affect the mean fields. There are a number of different ways of averaging

atmospheric data, the most frequently used of which are the average with

respect to longitude or 'zonal average', and the average with respect to time.

The concept of an ensemble average is also of importance.

The earliest studies of the global circulation were concerned with the

zonal average. It is easy to understand why. Most atmospheric variables

change much less in the zonal direction than they do in the vertical or in

the meridional directions. Indeed, the latitude of an observing site on the

Earth's surface is probably the most important single factor in determining

its climate. The zonal average of any scalar quantity Q is denoted [g], and

may be defined as:

[Q (2.1)

Alternatively, in terms of the distance x along the latitude circle,

[Q]

= j [

Qdx. (2.2)

Note that, by definition,

[Q]

is independent of longitude. The local value of

Q will generally be different from

[Q].

This deviation is variously called 'the