Jaeger G. Quantum Information: An Overview

Подождите немного. Документ загружается.

3.4 Gleason’s theorem 51

deﬁnite. However, the agent could just as well have checked the values of the

quantities corresponding to a diﬀerent basis, say the diagonal basis represented

by P (|)andP (|). But then these other values must also be deﬁnite.

Thus, the value of the states of both systems for all values of ξ must be

deﬁnite. The description of the system of particles by the quantum state |Ψ

−



is in this way argued to be incomplete.

3.4 Gleason’s theorem

A deﬁnitive theoretical result regarding the hidden-variables question and the

completeness of the quantum-mechanical description of physical systems is

Gleason’s theorem. This result is often considered to be the most signiﬁcant

technical advance in the foundations of quantum mechanics to be obtained af-

ter von Neumann’s initial investigation of the hidden-variables question. The

theorem demonstrates a sense in which the quantum statistical operators do

provide complete state descriptions [189]. It also clariﬁes the diﬃculties associ-

ated with putative hidden-variables descriptions touched on by von Neumann

without requiring the second of his assumptions, which is often viewed as

unwarranted.

A vital lemma underlying Gleason’s theorem is the following ([189]). Let

|φ and |ψ be two state-vectors in a Hilbert space H of dimension at least 3,

such that for a given system state P (|ψ) = 1 and P(|φ) =0.Then|φ and

|ψ cannot be arbitrarily close to one another. In particular, || |φ−|ψ||>

The physical system state is here taken to provide a map from each

projector, P

,toarealnumber,p(P

), between 0 and 1, p : P

→ p(P

such that p(O)=0andp(I)=1whereO is the projector onto the zero

vector 0 and I projects onto all of H,andsuchthatP

= 0 implies

p(P

+ P

)=p(P

)+p(P

); p is also taken to be a countably additive proba-

bility measure.

Gleason’s theorem: All probability measures that can be deﬁned on the

lattice of quantum propositions P

from the quantum statistical operators,

that is, all quantum probabilities, are of the form

p(P

) = tr(ρP

) , (3.6)

for some statistical operator ρ on H, for all H of dimension greater than two.

That is, the values corresponding to mutually orthogonal projectors are derivable

using a Born-type rule; see Postulate II of quantum mechanics in Appendix B

[68]. For a discussion of the lattice of quantum propositions formed from the

projectors P

, which represent bivalent quantities, see Appendix A. Gleason’s

lemma as presented above conforms to Bell’s re-derivation [32]. Gleason’s theorem

can be seen to provide a generalization of the Radon–Nikodym theorem. The trace

measure assigns to each projector the dimension of its range, which can then be

normalized by the dimension of the pertinent (ﬁnite-dimensional) Hilbert space;

52 3 Quantum nonlocality and interferometry

Gleason’s theorem shows that every probability measure over the set of

projectors arises from a statistical operator on the Hilbert space of the system

of interest, as expressed in Eq. 3.6. The relation of Gleason’s lemma to the

question of the possibility of hidden variables is the following. Consider puta-

tive dispersion-free states for which projectors would take expectation values

of either 0 or 1 under the mapping. The condition



P (|φ

) = 1 implies

that both values must occur, because there are no other possible values for

satisfying the condition and neither alone suﬃces. In this case, there must

be arbitrarily close pairs |ψ, |φ having diﬀerent expectation values, 0 and 1

respectively. However, such pairs cannot be arbitrarily close, by the lemma.

Therefore, there are no dispersion-free states. Thus, no theory is capable of ad-

equately reproducing quantum statistics via hidden variables parameterizing

dispersion-free probability measures [32].

Gleason’s results show the set of quantum states to be complete in the

sense that they yield the probability measures deﬁnable on the lattice of quan-

tum propositions corresponding to the projectors.

This result is still open to

a reasonable objection, however. Namely, it can be considered unnatural to

require dispersion-free states to provide nontrivial relationships between ex-

periments that cannot be made simultaneously.

3.5 Bell inequalities

John Bell famously further advanced the investigation of quantum behavior by

deriving a theorem in the form of a general inequality relation providing a clear

borderline between local classically explicable behavior and less intuitive forms

of behavior, such as nonlocality and contextuality as described in Section 3.1.

Following the lead of EPR, Bell deﬁned local models as follows. A local hidden-

variables theory for experimental situations of the EPR type is one such that

every complete state assigns a deﬁnite probability to a positive measurement

outcome for a bivalent property of one subsystem when the hidden parameter

describing it—taken to be capable of taking at least two values—takes a given

value independently of measurements performed on the other subsystem.

it is thus obtainable by considering ρ to be the maximally mixed state on the

space; see Sect. 1.5 of [348].

An extension of Gleason’s theorem to the setting of POVMs having implications

for the interpretation of quantum probabilities has recently been proven by Paul

Busch [91].

A natural, weaker requirement would be merely to require that quantum mechan-

ical averages over them do so. For a more detailed discussion of this argument,

see Ch. 1 of [30].

It is interesting to note that Bell had himself oﬃcially listed as a “quantum

engineer” in the CERN personnel directory. For a detailed survey of the work of

Bell, see [231].

John Jarrett showed Bell’s locality condition to be the conjunction of two in-

dependent conditions [243], later named parameter independence and outcome

3.5 Bell inequalities 53

This inequality is the prototype of the collection of inequalities now typically

referred to as the Bell inequalities.

Bell arrived at his crucial inequality for realistic hidden-variables theories

of the type that EPR had suggested might exist, as follows. He began by

considering a putative complete state, λ, describing a pair of particles, that

at a given instant fully speciﬁes all the elements of physical reality present in

the pair.

Any such state capable of giving rise to perfect correlations will

predetermine the outcomes of joint measurements of the component of spin of

these particles along a given direction, n

, for each particle i.Bellconsidered

a probability measure, µ(Λ), on the entire space Λ of parameters providing

complete states. Expectation values, E

µ(λ)

, of the relevant physical quantities

weretakentobeoftheform

µ(Λ)

, n



)dµ(λ) , (3.7)

where λ ∈ Λ,andA

)andB

) indicate measurement results along

directions n

on the two diﬀerent systems of the arrangement. He then arrived

at an inequality of the form

µ(Λ)

(a, b) − E

µ(Λ)

(a, c)|≤1+E

µ(Λ)

(b, c) , (3.8)

where {a, b, c} is any set of three angles specifying directions of measurement

in planes normal to the line of counter-propagation of the particles; see Fig.

3.1 [30, 32].

Issues regarding the assumptions used to derive this inequality, noted by

Bell himself and others, subsequently led to a search for other related inequal-

ities now also referred to as Bell inequalities (or Bell-type inequalities), based

on weaker assumptions.

In particular, the Clauser–Horne (CH) inequality

resulted from this investigation: classical probabilities must obey the relation

−1 ≤ p

+ p

− p

≤ 0 , (3.9)

as well as all the inequalities resulting from permutations of indices, where p

and p

are the probabilities that the ﬁrst particle is found along the ﬁrst of the

independence by Abner Shimony [382]. The term “Bell’s theorem” refers to a

collection of results having in common the demonstration of the impossibility of

a Local Realistic interpretation of quantum correlations.

The complete state as originally speciﬁed by Bell “determines the results of mea-

surements on the system, either by assigning a value to the measured quantity

that is revealed by measurement regardless of the details of the measurement

procedure, or by enabling the system to elicit a deﬁnite response whenever it is

measured, but a response which may depend on the macroscopic features of the

experimental arrangement or even on the complete state of the measured system

together with that arrangement” [386].

The full details of these other inequalities and assumptions can be found, for

example, in [32, 387].

54 3 Quantum nonlocality and interferometry

source

Fig. 3.1. Geometry of an apparatus for performing a test of Bell-type inequalities by

two-qubit polarization interferometry. Two nonorthogonal states of qubits Q and Q



are measured, parameterized by angles θ

and θ

, respectively, in the plane normal

to the direction of qubit counter-propagation. (Compare this arrangement with that

of the two-qubit spatial interferometer of Fig 3.2, below.)

four directions {a, b, c, d} and the second particle is found along the third di-

rection; p

stands for the joint probability of ﬁnding the ﬁrst particle along the

direction i and the second particle along direction j,1≤ i, j ≤ 4.

Because

in actual experimental situations it is generally impossible to have control of

the complete state of the total system, one assumes that the experimental ar-

rangement prescribes a probability distribution over state speciﬁcations that

provides the above probabilities through averages over Λ. No special restric-

tion is placed on Λ or the probability distribution used in the derivation of

the above result; indeed, the inequality follows from the elementary algebra

of numbers lying between 0 and 1, as probabilities must by deﬁnition.

In order to lend greater practicality to explorations of issues of hidden-

variables and locality, allowing them to be precisely probed by experiment,

John Clauser, Michael Horne, Abner Shimony, and Richard Holt (CHSH)

then also modiﬁed Bell’s original treatment so as to be applicable in any

practical experimental arrangement suﬃciently similar to that of the two-spin

atomic system that had been considered in experimental tests of locality-

related inequalities up until that time, arriving at what is now known as the

CHSH inequality:

|S|≤2 , (3.10)

for S ≡ E(θ

,θ

)+E(θ



,θ

)+E(θ

,θ



) − E(θ



,θ



) , (3.11)

where the Es are expectation values of the products of measurement outcomes

given parameter values θ

and θ



(the angles shown in Fig. 3.1) of the two

diﬀerent directions ˆn

for the same laboratory i relative to a reference direction

Recall that these particles correspond to qubit-pair systems.

3.5 Bell inequalities 55

[108].

The CHSH inequality is the Bell-type inequality now most commonly

referred to in the literature. The correlation coeﬃcients contributing to S can

be expressed in terms of experimental detection rates as

E(θ

,θ

C(θ

,θ

)+C(θ

⊥

,θ

⊥

) − C(θ

,θ

⊥

) − C(θ

⊥

,θ

)

C(θ

,θ

)+C(θ

⊥

,θ

⊥

)+C(θ

,θ

⊥

)+C(θ

⊥

,θ

)

, (3.12)

where the C(·, ·) are, in particular, coincidence detection count rates, i is the

index for particle 1, j the index for particle 2, and the parameter θ

⊥

indicates

a parameter corresponding to the direction perpendicular to that speciﬁed by

θ in the plane normal to the direction of particle propagation.

According to the predictions of quantum mechanics for noiseless quan-

tum channels, a maximum violation of this inequality by a factor of

√

can be achieve when, for example, one prepares the quantum state |Φ

 =

√



|00 + |11



,where|0 indicates photon polarization oriented along one

of the orthogonal axes of the plane indicated in Fig. 3.1 and |1 indicates po-

larization oriented along the other, and performs measurements with θ



=0,θ

,andθ



3π

,stepsof

radians, where the two angles in

each lab (that is, side) diﬀer by

radians, corresponding to

radians in the

Poincar´e–Bloch sphere; see [386] for an explicit calculation and Section 12.4

for an application. Since its introduction, the observed value of S has served

experimentalists as a ﬁgure of merit for the quantum nature of sources of

entangled quantum systems in such “Bell tests.” It is useful in this context to

introduce the so-called Bell operator

B≡ˆa · σ ⊗ (

b +



) · σ + ˆa



· σ ⊗ (

b −



) · σ , (3.13)

where ˆa, ˆa



are unit-vectors deﬁning the directions of the pertinent qubit

measurements, that is, the directions ˆn

and σ =(σ

,σ

). In particular,

the Bell operator can be used to provide a compact operator form of the

CHSH inequality via its expectation value, namely

B =tr(ρB) ≤ 2 . (3.14)

The Bell operator is also an “entanglement witness”; see Section 6.7. Quantum

mechanics provides an experimentally well conﬁrmed value near B =2

√

A further Bell-type inequality having a particularly simple proof assuming,

unlike the proof of the CHSH inequality, perfect anticorrelations for measure-

ments along parallel axes, was ﬁrst given by Eugene Wigner that has since

come to be known as the Wigner inequality,namely,

(a, b)+p

(b, c) − p

(a, c) ≥ 0 , (3.15)

The ﬁrst experiments to be studied to ﬁnd nonclassical behavior related to in-

vestigations of quantum nonlocality were those published in 1950 by Wu and

Shaknov [463], with spin qubits in a singlet state [66].

Note that the denominator simply provides normalization.

56 3 Quantum nonlocality and interferometry

where one agent, say that of a quantum-key distributor Alice, chooses between

two polarization measurements along directions a and b of one of two parti-

cles and another agent, say a quantum-key receiver Bob, similarly chooses

between measurements along b or c of the other [456]. The direction common

to the two parties, b, can be taken to be one of the elements of the reference

basis {|0, |1} for the corresponding optical polarization-coincidence experi-

ment described by Fig. 3.1, where a qubit state parallel to a given polarizer

state is considered a “+” result and a state orthogonal to the polarizer state

is a “−” result. If every particle were to have hidden variables determining

the outcomes of the measurements on the particles, the probabilities of “+”

measurement outcomes on both sides, p

(i, j), would obey this inequality.

The assumptions of the derivation of Wigner’s inequality are that measure-

ment outcomes on the two particles in identical directions are anti-correlated

and that measurement outcomes on the two particles are independent of each

another, with the background assumption that the probabilities involved re-

fer to the statistics of an ensemble of identically prepared particle pairs. The

quantum-mechanical probability for such a result along arbitrary directions,

and θ

, for a pair of particles in the Bell singlet state |Ψ

−

,namely,

(|Ψ

−

)=

sin

(θ

− θ

) , (3.16)

produces a maximal deviation from the satisfaction of this inequality when,

for example, a = −

,b = 0 and c =

, three directions

radians apart,

which provides a value of −

for the left-hand-side of Eq. (3.15). The Wigner

inequality has been recently used to perform entangled-state quantum key

distribution in practice; see [449].

Such violations of Bell-type inequalities by quantum mechanics have by

this time been studied in great generality. Because they rely on fundamen-

tal properties of probability, the expressions bounding the probabilities and

expectation values in these inequalities can be derived by, for example, enu-

merating all conceivable classical possibilities. These can be viewed as extreme

points spanning the classical correlation polytopes, the faces of which are ex-

pressed by Bell-type inequalities; see Section A.8. All Bell-type inequalities

involve sums of (joint) probabilities and expectation values. To show the in-

compatibility of the predictions of quantum mechanics with these inequalities,

the quantum counterparts and expectation values can be substituted for the

probabilities and expectation values appearing in them. The results systemati-

cally show the violation of such local-realistic bounds by quantum-mechanical

predictions.

Bell-type inequalities for pairs of systems of arbitrarily high

dimension have also been found [112].

All expressions entering the quantum expression corresponding to the pertinent

part of any Bell-type inequality are self-adjoint. Because the norm of the self-

adjoint transformation appearing in the inequality obeys the min-max principle,

ﬁnding the maximal violation of Bell inequalities corresponds to the solution of

a quantum eigenvalue problem, such as that for the Bell operator above. For a

3.6 Interferometric complementarity 57

3.6 Interferometric complementarity

Tests of the above Bell-type inequalities illustrate the importance of quan-

tum interference for probing nonlocal properties of quantum systems, partic-

ularly the interference of qubit pairs. Nonlocal interferometric behavior can

be examined in other illuminating ways as well. For example, there is a gen-

eral quantum interferometric complementarity relation between single-qubit

interference visibility, v

, and two-qubit interference visibility, v

,further

illustrating the surprising nature of quantum correlations exhibited in two-

particle interferometry [239]. In this regard, it was ﬁrst explicitly noted in

the late 1980’s that when the two-particle interference visibility is unity the

one-particle visibility is zero, and conversely [220]. In a doubled two-slit ex-

periment with a source of generic two-particle states, the former case can be

understood in terms of the washing out of photon self-interference due to un-

certainty of the initial direction of individual particles; see Fig. 3.2. In the

latter case, one notes that the arrival of one particle at one screen allows, in

eﬀect, two “virtual slits” to exist for the other due to the correlation between

them, corresponding to reduced relative uncertainties, giving rise to single-

particle interference [197]. A systematic investigation of intermediate cases

was carried out to further explore this relationship, demonstrating that such

a general complementarity relation holds for a large family of pure states |Θ,

deﬁned below [234].

A schematic illustration of the class of experimental arrangements in which

this complementarity can be exhibited is given in Fig. 3.2, namely, a dou-

bled version of the discrete two-beam experiment described in Section 1.5,

where the particle source produces generic pure two-particle states emerging

in beam pairs and transducers (variable beam-splitters together with sets of

phaseshifters) capable of exploring the full set of local unitary transformations

of two-qubit states (described by the group SU(2) × SU(2)) are introduced

(rather than merely 50–50 beam-splitters and single phaseshifters), followed

by pairs of particle detectors in two laboratories. Particle A is taken to be that

in beams 0 and/or 1, and similarly for particle B. Each pair contributing to

the output ensemble is produced by the source (say, by ﬁltered spontaneous

parametric down-conversion; see Section 6.16) in a two-qubit pure state

|Θ = γ

|0



+ γ

|0



+ γ

|1



+ γ

|1



, (3.17)

with γ

∈ C such that

|γ

+ |γ

=1, (3.18)

and |0

and |1

being basis vectors in the Hilbert space H

of the ﬁrst

particle corresponding to propagation in the beams 0 and 1, and |0



and



being similar vectors in the Hilbert space H

of the second particle.

more detailed exploration of this approach to Bell inequalities see, for example,

[336].

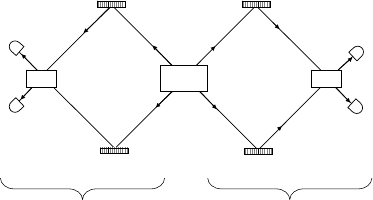
58 3 Quantum nonlocality and interferometry

source

Q' Q

Fig. 3.2. An interferometer containing two spatial qubits, Q and Q



. T indicates a

transducer capable of performing all local unitary transformations of a single qubit.

D indicates a particle detector. The laboratory of Alice is to the right and that of Bob

is to the left. (Compare with the arrangement of Fig. 3.1 describing interferometry

with polarization qubits under a more restricted class of measurements.)

Beams 0 and 1 are brought together in lab A at a transducer, T

, cor-

responding to a single-party unitary gate producing two output beams U

and L, and similar beams in lab B are brought together into another trans-

ducer, T

, implementing a similar gate that produces output beams, U



and L



, as indicated. The output beams are assumed to be equipped with

ideal particle detectors, D. As the transducers T

and T

are varied, the

probability P (UU



) of coincidence detection in beams U and U



, similar

joint-detection probabilities P (UL



), P (UL



), P (LL



), and single-detection

probabilities P (U ),P(L),P(U



),P(L



), corresponding to particle coincidence-

detection and single-detection rates, respectively, are modulated and can be

used to provide interferometric visibilities, as described below.

Given that |Θ = α|

0

+ β|

1

,whereα and β ∈ C with

|α|

+ |β|

=1, the vectors |

0 and |

1 being orthonormal (cf. Sect. 6.2),

the most general single-qubit local unitary transformation (LUT), T

,can

in this context be described as acting on particle A, providing an output

spatial-qubit state that can be written

0

= ae

iφ

|U + be

|L , (3.19)

1

= −be

−i

|U + ae

−iφ

|L , (3.20)

where a and b are real numbers the squares of which together sum to unity (cf.

Eqs. 1.12 and 1.30) and φ

and

being phase angles; similarly, for particle

B, providing a second output spatial-qubit state that can be written

0

= ce

iφ



 + de



 , (3.21)

1

= −de

−i



 + ce

−iφ



 , (3.22)

c and d also being real numbers, the squares of which together sum to unity,

and φ

and

are phase angles. The joint local operation of this pair of

3.6 Interferometric complementarity 59

transducers is described by the general pair of local unitary operations induced

by them separately, namely,

T = T

⊗ T

. (3.23)

Two-qubit interferometric behavior can then be studied via the modulation

of single-detection and joint-detection probabilities as T is varied over the full

range of parameters for the two LUTs, altering the above amplitudes and

phases [29]. From the maximum and minimum probabilities of detection, one

can calculate visibilities characterizing the interference. One is particularly

interested in the one-qubit interferometric fringe visibility

[P (Y )]

max

− [P (Y )]

min

[P (Y )]

max

+[P (Y )]

min

, (3.24)

where i = A, B, Y = U, L,andinV

, which is the two-qubit interferometric

visibility, in the sense of variations of detection probability as gates are var-

ied, calculable from the probabilities P (YY



) of occupation of the joint-paths



generalizing the case of the single paths Y above giving rise to the

single-qubit visibilities V

; for example,

[

P (UU



)]

max

− [

P (UU



)]

min

[

P (UU



)]

max

P (UU



)]

min

, (3.25)

where

P (UU



)=P (UU



) − P (U)P (U



(3.26)

represents nonaccidental coincidence probabilities and similarly for the three

other possible pairs of paths [234].

The remarkable phenomena that take place in two-qubit interferometry

result from the fact that, when the joint state |Θ is entangled, it can be the

case that

P (UU



) = P (U )P (U



) , (3.27)

and likewise for the other joint probabilities P (UL



), P (LU



), and P (LL



That is, highly correlated behavior of particles A and B arises due to quan-

tum entanglement. A strong complementarity relation, taking the form of an

equality [234], holds for all |Θ,namely,

+ V

=1, (3.28)

+ V

=1, (3.29)

Consider, as explicit examples, single and joint probabilities of the form of those

in Eqs. 3.36–37 for the related (Franson) conﬁguration of Sect. 3.7. (Also see Fig.

1.6 and Footnote 44 of Ch. 1.)

The constant term

)(

) added here compensates for the over-subtraction

of the constant “background” in the product of single-qubit probabilities, so that

only accidental modulation is subtracted from the “raw” coincidence probability.

60 3 Quantum nonlocality and interferometry

as has been explicitly experimentally conﬁrmed [2, 360].

The two complementarities we have by this point discussed, that between

path distinguishability and single-qubit visibility of Eq. (1.40) and that di-

rectly above, are closely related. In particular, the more entangled |Θ is,

the tighter the bound on the single-qubit visibility is. This result can be un-

derstood as follows. The information between basis vectors, |0 and |1,of

is related by the vectors in H

to which they can be correlated; ob-

servations made on only one particle of each pair cannot fully extract this

information. Similarly, a high degree of entanglement entails high two-qubit

interferometric-fringe visibility, and permits good inferences about the path of

particle A associated with spatial qubit Q from the results of measurements of

particle B associated with spatial qubit Q



. Indeed, V

is sometimes referred

to as the entanglement visibility (cf. [203]). The one-qubit interference visi-

bility thus enters into at least two complementarity relations, that between

single-qubit interference visibility and single-qubit bit-distinguishability (i.e.

path distinguishability, cf. Sect. 9.4) and that between single-qubit interfer-

ence visibility and two-qubit interference visibility (i.e. entanglement).

A distinction can be made between the “classical” and “nonclassical”

correlations of two qubits, which are manifested in the coincidence interfer-

ence visibility as described above. Consider a bipartite quantum system with

Hilbert space H = H

⊗H

and described by a statistical operator ρ. Recall

that such a state is uncorrelated if one can write ρ = ρ

(1)

⊗ρ

(2)

,whereρ

(i)

are

the statistical operators on the H

(i =1, 2). The expectation values of prod-

ucts of bounded linear operators A

(i)

on subsystems, such as the probabilities

of the form P (YY



) above, can then be factored, that is,



ρ(A

(1)

⊗ A

(2)

)



=tr



ρ(A

(1)

⊗ I)





ρ(I ⊗ A

(2)

)



(3.30)



i=1



(i)



. (3.31)

In this case, outcomes of measurements of the A

(i)

are such that the probabili-

ties of joint measurement outcomes are simply products of the probabilities of

outcomes of the measurements performed in the two laboratories. By contrast,

a statistical operator describing an ensemble wherein the quantum states of

the two portions of the total system are correlated, in that the subsystems ρ

(i)

are in the same state ρ

(j =1,...,n) with probabilities p

, can be written

as a convex combination of separable states,



j=1

⊗ ρ

. (3.32)

In that case, the expectation values of measurements of the properties A

(i)

are of the form

The ﬁrst experiments explicitly conﬁrming this complementarity relation were

performed in the Quantum Imaging Lab at Boston University [2, 360].