Jaeger G. Quantum Information: An Overview

Подождите немного. Документ загружается.

14.2 The Grover search algorithm 221

The phases do the work here. The result of the above operations is that

the output quantum state-vector for the ﬁrst n − 1 qubits in the case of

the constant functions lies entirely in the direction |0

⊗n−1

; in the case of the

balanced functions it lies entirely in the subspace orthogonal to this direction,

that is, it has no component along the |0

⊗n−1

direction. This allows the two

classes to be distinguished by a projective measurement of the binary property

of being an element of one subspace or not being so.

H H

|0Ó

|1Ó

Fig. 14.1. A quantum circuit implementing the pre-measurement portion of the

Deutsch–Jozsa algorithm for f : {0, 1}

×2

→{0, 1}. H indicates a Hadamard trans-

formation and U

the oracle. For an experimental three-qubit realization, see [413].

Any classical algorithm performing the same task requires the oracle f to

be evaluated a total number of 2

(n−1)

+ 1 times for the n-qubit version of the

Deutsch–Jozsa algorithm to obtain a certainly correct classiﬁcation; in the

case of the above example, this number is ﬁve. The algorithm generalizes in

the obvious way. This algorithm has already been carried out in several sorts

of system. Let us now consider an algorithm of greater practical import.

14.2 The Grover search algorithm

Database searching is a fundamental task of information processing, having

applications in cryptography, for example.

Given a database, one often de-

sires to ﬁnd a given one of its states among the set of its N possible states,

provided as an unsorted list. This is equivalent to the problem of ﬁnding a par-

ticular “target” entry in the database that is “marked” in a situation where

it is known that there exists one such entry in the database, because each

possible state of the database corresponds to having a distinct entry marked.

Lov Grover discovered a quantum algorithm for database searching having

an eﬃciency that surpasses that of classical search algorithms, providing a

quadratic speedup: a query taking O(N) steps classically can be performed in

For example, the 56-bit DES code can be broken with certainty by performing a

complete search over the 2

available possibilities [312].

222 14 Quantum algorithms

√

N) steps using this algorithm [199, 200]. Although less dramatic than the

speedup provided by quantum algorithms involving period ﬁnding (discussed

below),suchanimprovementis still signiﬁcant, just as, for example, the clas-

sical Fast Fourier Transform is of practical importance as an improvement

over the standard Fourier transform. The database involved in a search can

be accessed, similarly to how the function in the Deutsch–Jozsa algorithm can

be queried, using a representative binary oracle function f. The function in

this case is deﬁned over the pertinent set of states that takes the value 1 for

a given “marked” state and is 0 for all other states.

Database searching is an “NP-oracle problem,” a standard “oracle ideal-

ization” in which one has no internal access to the mechanism realizing the

black box function f. The quantum circuit corresponding to the Grover op-

erator, deﬁned below, can “recognize” the target state but cannot directly

provide its location. Rather, with each iteration, the central quantum circuit

rotates the quantum register by increasing the magnitude of the quantum

amplitude representing the actual database state relative to the amplitudes

corresponding to all other possible database states, allowing it eventually to

be distinguished from them. The oracle can be queried in this way as many

times as necessary in the course of carrying out the algorithm which, however,

involves only a prescribed number of queries. The best classical algorithm re-

quires

oracle evaluations, on average, to solve the database search problem

for an N-element database, whereas this algorithm requires only O(

√

N)or-

acle evaluations. The full Grover algorithm takes only O(

√

N log

N)steps.

The Grover search is carried out primarily by repeatedly applying the

unitary Grover operator, U

≡−I(|Ψ

)H

I(|m)H

, involving one oracle

query per iteration, beginning with an initial register state, |Ψ

,ofwhich

a given component |m is sought; H

is an n-qubit operation performing an

individual Hadamard transformation on every qubit state within the total

quantum system on which it acts; each operator of the Householder form

I(|Φ) ≡ I −2P (|Φ) inverts the register state by ﬂipping the sign of its vector

argument |Φ and leaving unchanged all the state-vectors orthogonal to it.

The oracle “marks” the target amplitude using I(|m)=I − 2P (|m).

I(|m) is a selective inversion about the hyperplane orthogonal to

the target state |m in a sense that is away from it within a plane S

deﬁned by |Ψ

 and |m; −I(|Ψ

) is a selective inversion in the op-

posite sense by a larger angle in S, back toward the target state. The

planar subspace S is invariant under the actions of both I(|m)and

I(|Ψ

). The net result of this pair of inversions is the pertinent rota-

tion in S, by twice the angle between the directions of |Ψ

 and |m,

one step toward the target state: the eﬀect of the (unitary) Grover

operator U

in each iteration is to provide a register superposition-

state rotated by ﬁxed-angle θ in this plane to a direction making a

smaller angle with that of the target state.

14.2 The Grover search algorithm 223

The result of a single Grover transformation is a rotational step (see the

box above). When this step is taken an appropriate number of times, a mea-

surement in the computational basis ﬁnds the register in the target state |m

with very high probability, in essence completing the search. The eﬀect of the

n + 1 qubits repeatedly encountering the corresponding Grover circuit is a

clock-like rotation of the register state by constant steps that progressively

“amplify” the component along the target state vector, so that the register ap-

proaches the ﬁnal state as the prescribed number of iterations is approached.

The initialized state for this algorithm is an N =2

–entry “unstructured

database,” where n is the size of the register R in qubits, that can be written

|Ψ

 =

√

N−1



i=0

|i

= H

⊗n

|0

⊗n

, (14.4)

where the index i counts over the 2

elements of the computational basis, that

is, all possible database states, of which one component, |m

,is“marked”

in the sense that the oracle picks it out. One adds a single ancillary qubit

in the diagonal-basis state |

, allowing the oracle output values f(i)to

inﬂuence the phases of the database amplitudes by giving |m

a minus sign;

the ancilla A can be referred to as the oracle’s qubit for this reason.

The initial state of the complete system of n-qubit register plus single

ancillary qubit A in the combined Hilbert space H

⊗H

is the product

|Ψ =

√

N−1



i=0

|i

|

(14.5)

√

N−1



i=0

|i

|0

−

√

N−1



i=0

|i

|1

. (14.6)

Then, in each iteration, the following transformations constituting the Grover

transformation take place, realizing the “amplitude ampliﬁcation” procedure,

beginning with the evaluation (or query)off.

i) For the “marked” state, there is a state reﬂection |m

→−|m

via

I(|m



I − 2P (|m)



⊗ I

. (14.7)

ii) All qubits are Hadamard transformed;

iii) For i = m, there is a state reﬂection |i

→−|i

via

−I(|Ψ







i=m

2P (|i) −I



⊗ I

. (14.8)

iv) All qubits are again Hadamard transformed.

After each iteration, the overall system R+A is in a product state. The an-

cillary qubit in H

is left in the same superposition state, |

,asatthe

224 14 Quantum algorithms

outset. By contrast, as a result of the above two inversions, the state in H

is left rotated by a net angle θ with each iteration, where

cos θ =1−

(14.9)

sin θ =2

√

N − 1

, (14.10)

and θ ≈ sin θ =

√

, bringing it closer to the target state |m

.Thus,the

after

√

N iterations, each inducing

a rotation by the ﬁxed angle θ, for a measurement to determine the state of

the database with high probability. Hence only O(

√

N) queries are needed,

an improvement over the O(N ) queries required by a classical algorithm.

To summarize: the computational state is progressively rotated so as to

allow for the identiﬁcation of the marked state; the resulting state is measured

after the required number of iterations, providing the the marked state among

the possible database states.

If the problem is instead such that there is more

than one marked state that is unknown, the situation is not greatly changed

as long as the number M of marked states is much smaller than the size of the

database, N. One can in that case choose, at random, the number of iterations

to be performed as a number between 0 and

√

, because the probability of

ﬁnding a marked state is close to 50 percent for every M. Any algorithm for

this problem will require O(



N/M) queries of the oracle.

The Grover search algorithm has been shown to provide an optimal search

in the sense that it cannot be parallelized better than by assigning diﬀerent

parts of the searching space to a number of independent quantum processors

[467].

14.3 The Shor factoring algorithm

The prime factoring of integers is of central importance to the security of

classical public-key cryptosystems: the ability to eﬃciently factor allows one

more easily to break cryptosystems that are dependent on the costliness of

performing this operation using classical computers; see Section 12.1. Prime

factoring was believed to be an NP problem because the diﬃculty of factoring

increases exponentially with the size of the input number, in marked contrast

to the “inverse” problem of multiplication which increases only polynomially

with the size of the input. However, in 1993, Peter Shor discovered an eﬃ-

cient quantum algorithm for factoring integers that reduces the number of

steps from the exponential time of exp(N

1/3

) steps classically required to the

polynomial time of N

steps [388, 390]. This speedup can be understood by

Note, however, that after the required number of iterations determined by the

size of the database, if left unmeasured, the state will move past the desired state,

overshooting it. Graphic illustrations of this rotation are often deceptive.

14.3 The Shor factoring algorithm 225

noting that the quantum version of the fast Fourier transform can be carried

out eﬃciently, since the number of quantum-parallel computations increases

exponentially with number with the number of bits involved.

Integer prime factoring is the discovery of the product of prime numbers,

each potentially appearing repeatedly in the product, equal to the compound

positive integer in question (see Eq. 14.16 below). Factoring a number N is

easy, once ﬁnding the multiplicative order of an arbitrary element of Z

has

been made easy, because integer factorization reduces to the problem of order

ﬁnding [301].

Order ﬁnding is performed in the Shor algorithm by carrying

out phase estimation, in particular, the estimation of the eigenvalues associ-

ated with eigenvectors of unitary operators. The phase-estimation algorithm,

in turn, makes use of the quantum version of the discrete Fourier transform.

We now examine these algorithmic elements individually before providing an

explication of the (relatively complex) Shor algorithm.

The quantum Fourier transform is the quantum version of the discrete

Fourier transform (DFT). Consider a function f that can be written as a

normalized vector of the form

f =

n−1



i=0

, (14.11)

where {β

} is an orthonormal basis for the vector space formed by functions

into C, and its discrete Fourier transform,

f. In a quantum-state description,

the β

form an orthonormal basis for the Hilbert space of the system. The

quantum Fourier transform corresponds to the operation

f =

n−1



i=0

→

n−1



i=0

¯c

f, (14.12)

which is linear and unitary.

The quantum Fourier transform accomplishes a

reduction of the number of steps required to perform this operation by acting

on the amplitudes of a quantum superposition-state. The quantum Fourier

transform (QFT) is similar in character to the classical fast Fourier transform

(FFT).

Here, Z

is the multiplicative group of units of the integers mod N , Z

,the

cyclic group of order N ;acyclic group is a group that can be generated by a

single element (the generator) by repeated multiplication.

It is also the case that ||

f|| = 1, as can be seen to be so by noting that a quantum

Fourier transform pair must obey the Parseval identity ||f || = ||

f||, which can

be thought of as the Pythagorean theorem for inner-product spaces, as does the

traditional Fourier transform.

The fast Fourier transform, originally used by Gauss and rediscovered by James

Cooley and John Tukey in 1965, reduces the number of steps needed to compute

the Fourier transform from 2N

to 2N log

N steps, by recursively reducing the

transform for a number N =2

to two transforms each of length N/2 [113, 178].

226 14 Quantum algorithms

TheQFTontheintegersmodulon has the desired eﬀect on basis states,

namely, the mapping

|x →

√

n−1



k=0

−2πixy/n

|y , (14.13)

where x, y are representatives of cosets x + nZ and y + nZ, respectively. How-

ever, the outcome of the quantum Fourier transform remains, in a sense,

hidden in the complex amplitudes of the output state, so that only global

properties such as the period of the function—which is fortunately what is

of interest in this case—can be eﬃciently determined. As an example, the

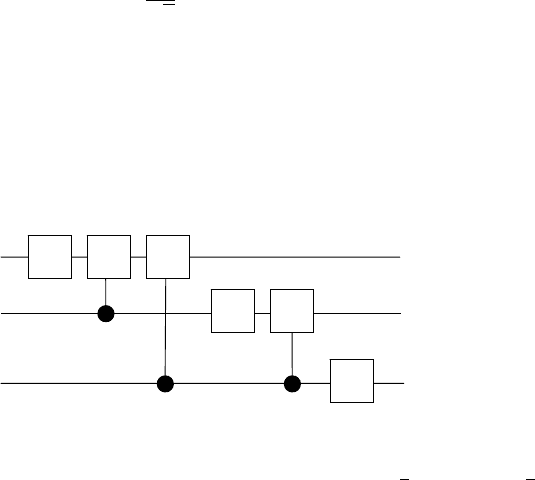
quantum circuit for performing a QFT on three qubits is shown in Fig. 14.2.

H P

ƍÓ

Fig. 14.2. A quantum circuit for carrying out the quantum Fourier transform on

three qubits for input computational basis states speciﬁed by the b

with outputs

speciﬁed by the b



. The H indicate Hadarmard gates and P

=P(

) and P

=P(

)

phase-shift gates.

The phase-estimation component of the Shor algorithm determines the

phase of a unit-magnitude complex eigenvalue from the solution of the eigen-

value problem of a unitary operator,

U|u = e

2πiφ

|u , (14.14)

making use of the QFT; the estimate is made via controlled-U operations

involving a pair of registers in the product state

|0

⊗n

|u

⊗n

. (14.15)

The ﬁrst register is acted on by an n-qubit Hadamard transformation and

functions as an array of n control qubits for a sequence of controlled-U

operations acting on collections of m qubits of the second register, where

the power m is equal to the position of the control qubit in its register. An

inverse discrete Fourier transform is then applied by the algorithm to the ﬁrst

the phase-estimation problem upon measurement in the computational basis.

14.3 The Shor factoring algorithm 227

By the fundamental theorem of arithmetic, the prime-factored form of any

positive integer N is

N = p

···p

, (14.16)

where p

are the primes and α

their powers, which are found using the (clas-

sical) Euclidean algorithm and a method of determining periods of (periodic)

functions. The central component of the Shor algorithm, which is summarized

brieﬂy below, is the process of order ﬁnding, which makes use of the quantum

phase-estimation procedure discussed above to assist in ﬁnding periods.

To factor N, consider an integer y between 1 and N −1. One can use the

(classical) Euclidean algorithm to ﬁnd whether gcd(y,N)=1,inO((log

)

(classical) steps. If gcd(y,N) > 1, this y is a desired nontrivial factor of N.

Otherwise, i.e. if gcd(y, N) = 1, one takes the (base N) order of y to be r,

that is, r =ord(y), y

=1(modN)andN divides y

− 1. If r is even, then

−1 is readily factored as (y

r/2

−1)(y

r/2

+1); N necessarily has a factor in

common with at least one of the elements of this product, which is similarly

found using the Euclidean algorithm. A function of the form

(x)=y

mod N, (14.17)

is periodic because f

(x + r)=f

(x); when f has period r, which is the case

here, a

= a

=1.

To obtain the period, one takes a number of the form

M =2

as the length of the Fourier transform, where N

≤ M ≤ 2N

allowing it to be eﬃciently performed, as below. With an eﬃcient process for

obtaining a nontrivial factor thus in hand, one applies it recursively to all

factors until the full factorization of the form of Eq. 14.16 is obtained.

Factoring can therefore be carried out in the Shor algorithm as follows.

(i) Randomly choose an integer y between 1 and N − 1, and ﬁnd gcd(y, N).

If gcd(y, N) > 1, y is a nontrivial factor; otherwise, proceed.

(ii) Prepare two quantum registers in a tensor product state, one of m qubits

for the arguments and a second one of m



= log

N qubits for the values

of the periodic function, with each qubit taking the zero bit-value in the

computational basis

|Ψ = |0

|0

, (14.18)

where |0

= |0

⊗m

and |0

= |0

⊗m



A function f(t) is periodic, with period T , if for all t, f (t + T)=f (t), where T

is a positive number.

Here, again, most normalization factors have been omitted, cf. [60].

Note that the number m



of qubits can be exponentially smaller than the period

of the function f

(x).

228 14 Quantum algorithms

(iii) Perform the Hadamard transform on every one of the m qubits of the

ﬁrst register, providing a superposition of all possible input number values,

resulting in the state

|Ψ



 =

M−1



x=0

|x

|0

. (14.19)

(iv) Compute the function f

(x)=y

mod N for each x using a unitary

transformation taking |x|0 →|x|y

mod N, to obtain

|Ψ



 = ξ

M−1



x=0

|x

mod N

, (14.20)

where ξ provides normalization.

(v) Measure the second register in the computational basis, obtaining a value

, leaving the system in the quantum state

|Ψ



 =

K−1



k=0

+ kr



, (14.21)

where the ﬁrst register is placed in a uniform superposition of all states |x for

which f

(x)=z

,wherey

= z

and K = '

(. The second register serves

to prepare the ﬁrst register; the particular value z

obtained in the process

has in itself no signiﬁcance for the operation of the algorithm.

(vi) Perform the (inverse) quantum Fourier transform on the ﬁrst register,

leaving the system in the state

|Ψ



 =

M−1



l=0

K−1



k=0

2πi(x

+kr)l/M

|l



, (14.22)

with the eﬀect that x

in the basis of the ﬁrst register appears now in the

phases of the superposition instead of the kets, “inverting” the periodicity of

the input.

(vii) Measure the ﬁrst register in the computational basis, providing the phase

estimate from among the values of l.

(viii) Given the result, which has beneﬁted from the speedup provided by

quantum parallelism, the period r of the function is then determinable by

classical computational methods.

The order, and hence a nontrivial factor,

is obtained.

The above process is repeatedly applied until the full prime factorization,

Eq. 14.16, is obtained.

For example, see the discussion in Sect. 4.5 of [60].

14.4 The Simon algorithm 229

14.4 The Simon algorithm

Factoring using the Shor algorithm involves ﬁnding the period of a function.

Another algorithm that involves this is Simon’s algorithm [60, 394], which is

an instance of a more general problem, the Abelian hidden-subgroup problem.

Given a function f from (Z

)

to itself (cf. Section A.1), representable as

a unitary map

|x|0 →|x|f(x) , (14.23)

for all x, that can be evaluated on quantum states in the presence of a sub-

group

H ∈ (Z

)

on which f takes a constant unique value on each right

coset of

H, Simon’s problem is to ﬁnd the generators of this subgroup. Si-

mon’s algorithm uses a number, of order O(N), of evaluations of the oracle

f, classical computation, and a polynomial number of quantum operations to

solve the problem. This algorithm operates as follows.

(i) Prepare two N-qubit quantum registers in tensor product states wherein

each qubit has the computational-basis-value zero,

|Ψ = |0

⊗N

|0

⊗N

. (14.24)

(ii) Perform a multiple-qubit Hadamard transformation on all qubits of the

ﬁrst register, providing a superposition of all possible inputs, namely,

|Ψ



 =

√



x∈(Z

)

|x

|0

. (14.25)

(iii) Act on this superposition with the unitary operation corresponding to f,

yielding

|Ψ



 =

√



x∈(Z

)

|x

|f(x)

. (14.26)

(iv) Measure the second register, obtaining a value y from the second register

and the coset of the hidden subgroup

H in the ﬁrst register:

|Ψ



 =





f(x)=y

|x

|y

. (14.27)

(v) Apply the multiple-qubit Hadamard transformation to the ﬁrst register.

(vi) Measure the ﬁrst register in the computational basis.

(vii) Repeat the above steps the anticipated number



that is, O(N)



of times,

generating with high probability the orthogonal complement of

H with respect

to the scalar product in (Z

)

(viii) Solve linear equations, for example, via Gauss’ classical algorithm for

ﬁnding the kernel of a square matrix, to obtain the generators of