Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

380 Chapter 9

The seniority concept represents the time spent by a member in the company

since his first entrance. As often it is possible to have fictive seniority at the

entrance time of the member, for example to attract competent members in

specialized fields, this initial seniority will be represented by the non-negative

random variable

0

S .

We give some constraints to seniority, more precisely:

- seniority cannot be greater then 0 at an initial work age

α

, for example 18,

- in a first statement of our model, seniority continues to increase also after

retirement.

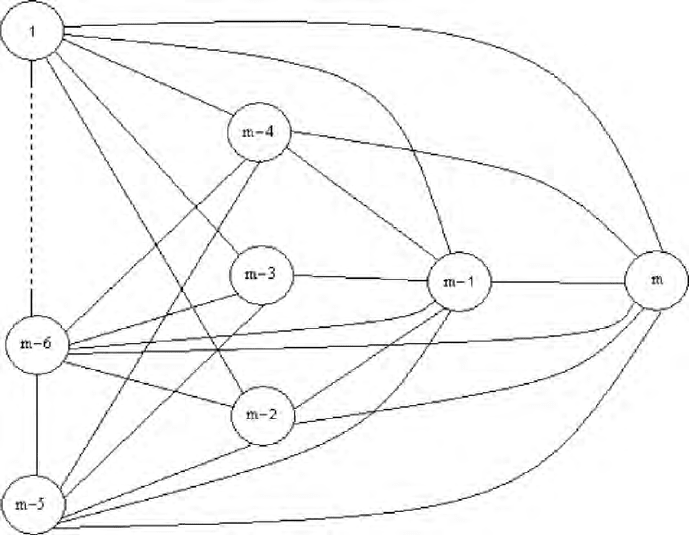
Figure 1.1: pension fund transitions

The second constraint can appear wrong, but once the pension is fixed (at

retirement age) there are no financial influences on the fund, moreover in this

way we know the fictive number of years that a person has in the fund.

In the following we will also present a version of the model with maximum

seniority. This model will be more tortuous then the one that we are going to

present.

The seniority , 1

n

Sn≥ is usually defined by the relation:

11

,0.

nnnn

SSTTn

++

=

+− > (1.18)

Generalized NHSMP models

381

For some members, it may however be necessary to add another fictive seniority,

due to an exceptional promotion for example.

The introduction of the new stochastic process

(, 1)

n

SSn

=

≥ implies that now,

at each state transition time n, the considered member of the fund is characterized

by the triple ( , , ), 1

nn n

J

TS n≥ .

Our new assumption will be that this (J,T,S) process is a bi-dimensional non-

homogeneous Markov renewal process (J,(T-S)) with as kernel:

¨1 1 1

(,) ( , , , , )

ij n n n n n n

Qst PJ jT tS t sJ iT sS

τ

+++

==≤≤+−===

. (1.19)

Probabilities defined in the preceding section only for the (J,T) process may be

easily extended to the (J,T,S) process as follows:

¨1 1 1

(,) ( , , , , )

ij n n n n n n

bst PJ jT tS t sJ iT sS

τ

+++

====+−=== (1.20)

so that:

(,) (, )

t

ij ij

hs

Qst bsh

ττ

=

∑

. (1.21)

Similarly, if we define:

(

)

1

() ,

ij n n n

p

sPJ jJiTs

+

=

=== (1.22)

we have:

() (, )

ij ij

ps Qs

ττ

=

∞ . (1.23)

These other following extensions are straightforward:

1

(,) (,)

m

iij

j

Hst Qst

ττ

=

∑

(1.24)

where:

(

)

() 1

,,

ist n n n n

HPTtJiTsS

τ

+

=≤===, (1.25)

(, ) 1

i

Hs

τ

∞

= , (1.26)

(,)

(,) ,

()

ij

Qst

Fst

p

s

τ

= (1.27)

where

(

)

11

(,) , , ,

ij n n n n n

Fst PT tJ iJ jT sS

τ

++

=≤====, (1.28)

i.e. the sojourn time conditional distribution entering in state i at time transition

n with a seniority

τ

.

Finally, it is also possible to define the two-dimensional semi-Markov process

associated with the two-dimensional NHMRP (J,(T-S)) noted as

((),, 0)ZZtt

τ

=

≥ , (1.29)

()

Z

t

τ

representing, for each time t, the state occupied by the member of

seniority

τ

.

The transition probabilities of this last process are given by:

382 Chapter 9

(

)

(,) () ()

ts

ij

s

tP Zt jZsi

τττ

φ

+−

=

== (1.30)

satisfying the analog system complying with (1.17):

11

(,) (1 (,)) (, ) ( ,)

mt

s

ij i ij ik kj

ks

s

tHst bs t

ττ ττϑ

ϑ

φ

δϑφϑ

+−

==+

=− +

∑∑

. (1.31)

To conclude this section, we can say that:

- the introduction of the concept of seniority is mathematically tractable,

- the introduction of seniority represents the first generalization step,

- the problem of getting data will be studied later.

1.3 The Reserve Structure

To apply this model to the pension fund problem we need to consider a reward

structure connected with the semi-Markov process representing the financial

charges and incomes of the considered fund.

Let us define now:

(,)

i

Vst

: the discounted expected reserve at a fixed epoch of the reward in the

time interval

[

)

,

s

t , given that there is an entrance in state i at age s,

i

ψ

: the amount paid per time period in state i (permanence reward),

r: the fixed rate of interest,

hr

a : the present value of a unitary h-period annuity i.e.:

1

(1 ) .

h

k

hr

k

ar

−

=

=+

∑

(1.32)

The evolution equations are the following ones:

11

(,) (1 (,)) (, )

(, ) ( ,)(1 ) ,

tm

iii ii

tsr sr

s

tm

s

i

s

Vst H st a b s a

bs V t r

β

θ

θβ

θ

ββ

θβ

ψθψ

θθ

−−

=+ =

−

=+ =

=− +

++

∑∑

(1.33)

1,..., ;im= 0 ;

s

t

≤

≤ , 0,1,....st=

In this case, the ( , )

i

Vst are the discounted expected values of the reserves that

have been paid from s to t when a member has arrived in state i at age s.

The term (1 ( , )

i

H

st

−

) represents the probability to remain in state i once a

member has arrived there at age s, a member having to pay (or to get) at each

period of time the reward

i

ψ

. This first term represents, as already explained in

Chapter 4, the expected value of this amount.

The second term of (1.33) gives the expected present value of the rewards that a

member arrived in i at age s paid in this state before changing the state.

The last term of relation (1.33) represents the expected value of the reserves that

a member who arrived in state i at age s and changed his situation at age

θ

has to

Generalized NHSMP models

383

pay in the other state. These values are discounted at time

θ

, so we need to

discount them at time s.

As with the evolution equations (1.33) it is not possible to allow for different

behaviors as a function of the seniority of people. We need to change the

evolution equations of the reserve process to introduce a seniority factor,

generalizing also the reward process, as we did for the semi-Markov process.

In this light, the relations (1.33) become:

11

(,) (1 (,)) (, )

(, ) ( ,)(1 ) .

tm

iii ii

tsr sr

s

tm

ss

i

s

Vst H st a b s a

bs V t r

τττ ττ

β

θ

θβ

ττθ θ

ββ

θβ

ψθψ

θθ

−−

=+ =

+− −

=+ =

=− +

++

∑∑

(1.34)

The meaning of (1.34) is analogous to that of (1.33), the only difference being

that now it is moreover possible to consider seniority. In this way, the

probabilities of changing states because of seniority, and moreover, it is possible

to consider also different rewards as a function of different seniorities namely:

,0,1,,

i

im

τ

ψτ

≥=… . (1.35)

1.4. The Impact Of Inflation And Interest Variability

To begin with, let us point out that it is important to make some assumptions on

the moments of the reward payment and of the state changes, because we are

working with discrete time models.

Our main assumptions are the following:

i) amounts of money are paid entirely at the midpoint of our period (we can

suppose that the period is one year, for example),

ii) changes always happen at the midpoint but after the reward payment.

Figure 1.2 illustrates this assumption.

Figure 1.2: payment and state change instants

In general, rewards are also time dependent but we still assume that it is not the

case, because the evolution equations of DTNHSMP are not involved in this

change. We only suppose that the transition probabilities change in time but only

because of age and seniority.

Another important point is to take into account both inflation and interest rate

variability, the latter being represented by the variations of the yield curve so that

384 Chapter 9

the model can measure the impact of the interest risk or of a change of an interest

scenario.

Let us thus introduce:

0, 1,...,

i

ri w>= , (1.36)

representing the successive interest rates in our time horizon,

[

]

0, w being the

time interval that we consider for the simulation.

From these values, taking into account the hypotheses that we made, we can

construct the present value factors.

Let us be precise that we need to consider two different kinds of factors: one,

'

ν

,

for the present value of the reward and the other,

ν

for discounting the (,)

i

Vst

τ

,

0, 1,..., .

h

rh w>=

Furthermore we now can introduce for the amount

i

τ

ψ

a new dependence on the

time h. We will note:

()

i

h

τ

ψ

, , 1, , ; 0, ,hi mh w

τ

≥= =……. (1.37)

Figure 1.3 describes the reward payment process.

Figures 1.4 and 1.5 describe the two different discounting processes and after

them the related formulas are reported:

Figure 1.3: reward payments

Figure 1.4: discount factors of reward payments

Figure 1.5: discount factors of reward process

We need a different discounting process. Indeed, the ( , )

i

Vst

τ

are discounted

always at the initial moment and the related discount factors will be ( , )

s

t

ν

. The

sums received or paid by the fund instead will be discounted by the '( , )

s

t

ν

considering one half period more.

After these assumptions that also take into account the passage of time, the

evolution equations for a discrete time non-homogeneous semi-Markov pension

reserve process DTNHSMPRP are:

Generalized NHSMP models

385

1

,

1

11

,

11

(,) (1 (,)) () '(, )

(, ) ( ) '(, )

(, ) ( ,)(, )

hts

hkh

ii i

kh

tm hs

kh

ii

skh

tm

sh s

i

s

Vst H st k hk

bs k hk

bs V t hh s

τττ

θ

ττ

β

θβ

ττθθ

ββ

θβ

ψν

θψν

θθνθ

+−−

+−

=

+−−

+−

=+ = =

+− +−

=+ =

=−

+

++−

∑

∑∑ ∑

∑∑

(1.38)

with

1

(,) (1 ) , (,) 1

hk

h

hk r hh

α

νν

+

−

=+

=

+=

∏

, (1.39)

1

1.5

'( , ) (1 ) (1 )

hk

h

hk r r

α

ν

+−

−

+

=

=++

∏

. (1.40)

Let us say once more that the reserve

,

(,)

h

i

Vst

τ

represents the mean present value

at time h of all the rewards that were paid to members of seniority

τ

of age s at

time h up to age t.

The next figure gives support for an example to explain formula (1.38).

0

12

3

60

61 62

63

35

36 37

38

Figure 1.6: time axes

62

35 35

60 1

(60,62) (60, )

m

iij

j

Hb

θ

==

=

∑∑

, (1.41)

1

35,0 35 35

0

01

35 35 35 35

(60,61)

10 1 0

35 36,1 35 37,2

11

(60,62) (1 (60,62)) ( ) '(0, )

( ) '(0, ) (60,62) ( ) '(0, )

(60,61) (61,62) (0,1) (60,62) (62,62) (0,

k

iii

k

mm

kk

ii i i

kk

mm

ii

VH kk

bkkb kk

bV b V

ββ

ββ β β

ββ

ψν

ψν ψν

νν

+

=

++

== = =

==

=−

++

∑

∑∑ ∑ ∑

∑∑

2).

(1.42)

1.5. Solving Evolution Equations

The equations (1.32) and (1.38) can be written in matrix form as follows:

1

(,) ( (,)) (, ) ( ,)

t

s

tst s t

ττ ττθ

θ

+−

=+

=− +

∑

Φ IH B Φ , (1.43)

386 Chapter 9

1

,

1

,

1

(,) ( (,)) ( ) '(, )

(, ) () '(, )

(, ) ( ,)(, ),

hts

hkh

kh

ths

kh

skh

t

sh s

s

tst khk

skhk

sthhs

τττ

θ

ττ

θ

ττθθ

θ

ν

θν

θθνθ

+−−

+−

=

+−−

+−

=+ =

+− +−

=+

=−

+

++−

∑

∑∑

∑

VIH ψ

B ψ

BV

(1.44)

where ( , ), ( , ), ( , )

s

tstst

τττ

Φ HB are square mm

×

matrices,

,

(,)

h

s

t

ν

V an m

vector and where:

0

s

t

τ

≤

≤≤

, , , ,sth

τ

∈

 , (1.45)

(,) (1 (,))

ij i

s

tHst

τ

δ

⎡

⎤

=−

⎣

⎦

H , (1.46)

1

2

()

k

m

k

τ

ψ

+

⎡

⎤

⎢

⎥

⎢

⎥

=

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

ψ



. (1.47)

If we want to solve the two evolution equations for a finite time horizon

considering the same period for both random variables

n

S

and

n

T

, i.e. we are

considering

w periods, we have:

0;

s

thw

τ

ω

≤

≤≤≤ ≤ (1.48)

instead of (1.46) and then formulas (1.44) and (1.45) hold;

ω

represents the

maximum reachable age.

The particular structure of systems (1.46) and (1.45) implies that no matrix

inversion is necessary to get the solutions. In fact, in the case of (1.44) we have:

(,)

w

ωω

=

Φ I , (1.49)

1

(,)

w

ωω

−

=

Φ I

, (1.50)

1

(1,1)

w

ωω

−

−=Φ I , (1.51)

11 1

(1,) (1,)(,)( (1,))

wwww

ω

ωωωωω ωω

−− −

−= − +− −Φ B Φ IH . (1.52)

The last relation gives the value of

1

(1,)

w

ω

−

−Φ and as:

2

(,)

w

ωω

−

=

Φ I , (1.53)

2

(1,1)

w

ωω

−

−=Φ I

, (1.54)

221 2

( 1,) ( 1,) (,) ( ( 1,))

www w

ω

ωωωωω ωω

−−− −

−= − +− −Φ B Φ IH , (1.55)

2

(2,2)

w

ωω

−

−=Φ I , (1.56)

we find the following "backward" values:

221

2

(2,1) (2,1) (1,1)

( ( 2, 1)),

www

w

ωω ωω ωω

ωω

−−−

−

−−= −− −−

+− − −

Φ B Φ

IH

(1.57)

Generalized NHSMP models

387

221

22

(2,) (2,1) (1,)

(2,)(,)( (1,)).

ww w

ω

ωωω ωω

ωω ωω ωω

−− −

−−

−= −− −

+− +− −

Φ B Φ

B Φ IH

(1.58)

To go on with this special case of "backward substitution" we finally obtain:

0

(,)

αα

=

Φ I , (1.59)

001 0

(, 1) (, 1) ( 1, 1) ( (, 1))

αα αα α α αα

+= + + ++− +Φ B Φ IH , (1.60)

001

02 0

(, 2) (, 1) ( 1, 2)

( , 2) ( 2, 2) ( ( , 2)),

αα αα α α

αα α α αα

+= + + +

++ +++− +

Φ B Φ

B Φ IH

(1.61)

00 0

1

(, ) (,) (, ) ( (, ))

ω

θα

α

ωαθθωαω

−

=+

=+−

∑

Φ B Φ IH

. (1.62)

Now we will show how this special kind of “backward substitution” proceeds.

We have a five indices matrix, this matrix can be seen as a three-dimensional

matrix whose elements are m-order square matrices.

In

Figure 1.7 is shown the case in which 5

ω

α

−

= and the number near the

matrix represents seniority. For each seniority, we have a block matrix. First of

all we can find the value of the unique element that is in the block matrix 5. Once

we know this element we can find the three elements of the matrix 4; working on

these elements with a “backward substitution”, in the same way it is possible to

compute the elements of the block matrix 3 and so on up to the matrix indexed

by 0.

0, 1, 2, 3,

4, 5

••••••

⎡⎤⎡⎤⎡⎤⎡⎤

⎢⎥⎢⎥⎢⎥⎢⎥

••••• •••••

⎢⎥⎢⎥⎢⎥⎢⎥

•••• •••• ••••

⎢⎥⎢⎥⎢⎥⎢⎥

••• ••• ••• •••

⎢⎥⎢⎥⎢⎥⎢⎥

•

•••••••

⎢⎥⎢⎥⎢⎥⎢⎥

••••

⎢⎥⎢⎥⎢⎥⎢⎥

⎣⎦⎣⎦⎣⎦⎣⎦

⎡⎤⎡⎤

⎢⎥⎢⎥

••

⎢⎥⎢⎥

••

⎢⎥⎢⎥

⎣⎦⎣⎦

Figure 1.7: the GDTNHSMP backward substitution

Equations (1.45) have the same structure and so can be solved by a backward

substitution, but with different indexes; for this reason we think it would be

better to show also in this case how this process works.

388 Chapter 9

We refer to the example shown at the end of the previous paragraph. In the

following are described the matrix formulas of the "backward substitution" for

this case.

,0

(,)

w

ωω

=

V0, (1.63)

,1

(,)

w

ωω

=

V0, (1.64)

1,0

(1,1)

w

ωω

−

−=V0

, (1.65)

0

1,0 1 1

0

11 1,1

( 1, ) ( ( 1, )) (0) '(0,0)

( 1, ) (0) '(0,0) ( 1, ) ( , ) (0,1).

www

k

ww ww

ωω ωω ν

ωω ν ωω ωων

−−−

=

−− −

−=− −

+− + −

∑

VIH ψ

B ψ BV

(1.66)

Using now result (1.64), we solve (1.66).

For the following steps we have:

,2

(,)

w

ωω

=

V0, (1.67)

1,1

(1,1)

w

ωω

−

−=V0, (1.68)

1

1,1 1 1

1

11 1,2

( 1, ) ( ( 1, )) ( ) '(1, )

( 1, ) (1) '(1,1) ( 1, ) ( , ) (1, 2),

www

k

ww ww

kk

ωω ωω ν

ωω ν ωω ωων

−−−

=

−− −

−=− −

+− + −

∑

VIH ψ

B ψ BV

(1.69)

2,0

(2,2)

w

ωω

−

−=V0, (1.70)

0

2,0 2 1

0

22

21,1

(2,1)( (2,1)) ()'(0,)

( 2, 1) (0) '(0,0)

(2,1) (1,1)(0,1),

www

k

ww

kk

ωω ωω ν

ωω ν

ωω ωων

−−−

=

−−

−−=− −−

+−−

+−− −−

∑

VIH ψ

B ψ

BV

(1.71)

1

2,0 2 2

0

1

22

10

2,2

1

( 2, ) ( ( 2, )) ( ) '(0, )

(2,) ()'(0,)

(2,) (,)(0, 2).

wwwk

k

wwk

k

ww

kk

ωθω

θω

ω

θωθω

θω

ωω ωω ν

ωθ ν

ωθ θωνθω

−−−+

=

−+

−−+

=− =

−++−+

=−

−=− −

+−

+− −+

∑

∑∑

∑

VIH ψ

B ψ

BV

(1.72)

In this way we can get the solutions of (1.72) knowing the previous results.

At last let us describe the solution for people that were at age

α

and seniority

equal to 0 at the beginning of the simulation. We have successively:

,

(,)

ww

ωω

=

V0, (1.73)

1, 1

(1,1)

ww

ωω

−−

−

−=V0

, (1.74)

Generalized NHSMP models

389

1

1, 1 1 1

1

11

11,1

( 1, ) ( ( 1, )) ( ) '( 1, )

(1,) (1)'(1,1)

(1,) (1,)(1,),

w

ww w w

kw

ww

www

kwk

www

ww

ωω ωω ν

ωω ν

ωω ωων

−

−− − −

=−

−−

−−−

−=− − −

+− −−−

−−−

∑

VIH ψ

B ψ

BV

(1.75)

and at last

0,0

(,)

αα

=

V0, (1.76)

0

0,0 0

0

00 01,1

(, 1) ( (, 1)) ()'(0,)

( , 1) (0) '(0,0) ( , 1) ( , 1) (0,1),

k

kk

αα αα ν

αα ν αα αα ν

=

+=− +

++ + + +

∑

VIH ψ

B ψ BV

(1.77)

1

0,0 0

0

21

0

10

2

0,

1

(, 2) ( (, 2)) ()'(0,)

(,) ()'(0,)

(,) (, 2)(0, ),

k

kk

αθα

θα

α

θαθα

θα

αα αα ν

αθ ν

αθ θα ν θ α

=

+−−

=+ =

+

−−

=+

+=− +

+

++−

∑

∑∑

∑

VIH ψ

B ψ

BV

(1.78)

1

0,0 0

0

1

0

10

0,

1

(,) ( (,)) ()'(0,)

(,) ()'(0,)

(,) (,)(0, ).

k

kk

ωα

ωθα

θα

ω

θαθα

θα

αω αω ν

αθ ν

αθ θων θ α

−−

=

−−

=+ =

−−

=+

=−

+

+−

∑

∑∑

∑

VIH ψ

B ψ

BV

(1.79)

1.6. The Dynamic Population Evolution Of The Pension

Funds

We will now immediately consider an open pension scheme in a way which is

defined below.

Let us begin with the following definitions:

,

()

h

i

N

s

τ

: the number of members present in the fund at time h with seniority

τ

,

age s and in state i,

,

()

h

N

s

τ

: the number of members present in the fund at time h with seniority

τ

and age s,

,h

i

N

τ

: the number of members present in the fund at time h with seniority

τ

and

in state i,

,h

N

τ

: the number of members present in the fund at time h with seniority

τ

,

Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

Подождите немного. Документ загружается.