Jacques I. Mathematics for Economics and Business
Подождите немного. Документ загружается.

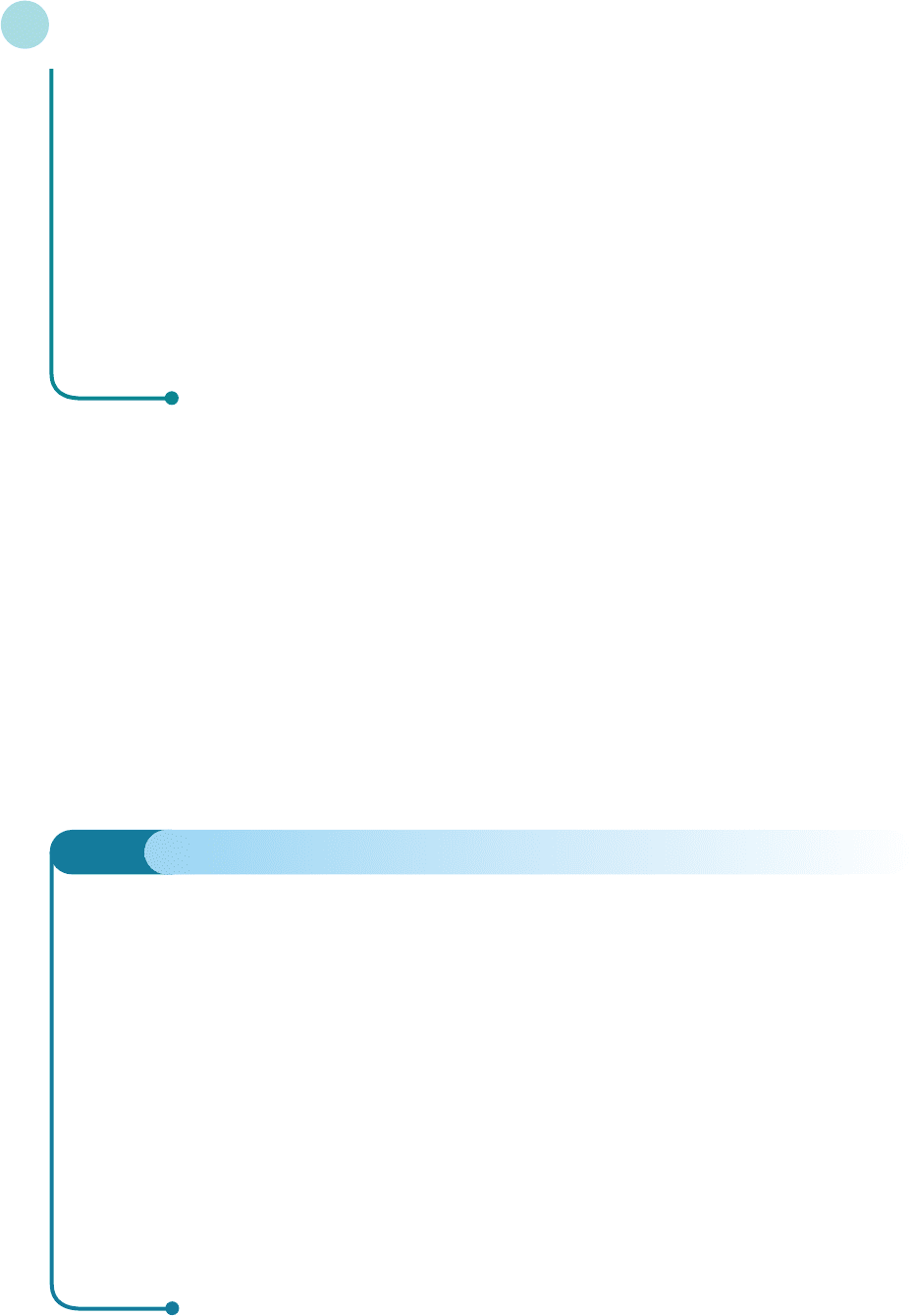
Solution
(a) 2A =
(b) −A = (−1)A =
(c) 0A ==0
J
K
K
L
000
000
000
G
H
H
I
J
K
K
L
−1 −2 −3
−4 −5 −6
−7 −8 −9
G
H
H
I
J
K
K
L
246
81012
14 16 18
G
H
H
I
Matrices
460
In ordinary arithmetic we know that
a(b + c) = ab + ac
for any three numbers a, b and c. It follows from our definitions of matrix addition and scalar
multiplication that
k(A + B) = kA + kB
for any m × n matrices A and B, and scalar k.
Another property of matrices is
k(lA) = (kl)A
for scalars k and l. Again this follows from the comparable property
a(bc) = (ab)c
for ordinary numbers.
You are invited to check these two matrix properties for yourself in the following problem.
Practice Problem
4 Let
A = and B =
(1) Find
(a)
2A (b) 2B (c) A + B (d) 2(A + B)
Hence verify that
2(A + B) = 2A + 2B
(2) Find
(a)
3A (b) −6A
Hence verify that
−2(3A) =−6A
J
K
K
L
0 −1
27
16
G
H
H
I
J
K
K
L
1 −2
35
04
G
H
H
I
MFE_C07a.qxd 16/12/2005 10:45 Page 460

7.1.4 Matrix multiplication
7.1 • Basic matrix operations
461
Advice
Hopefully, you have found the matrix operations considered so far in this section easy
to understand. We now turn our attention to matrix multiplication. If you have never
multiplied matrices before, you may find that it requires a bit more effort to grasp and
you should allow yourself extra time to work through the problems. There is no need to
worry. Once you have performed a dozen or so matrix multiplications, you will find that
the technique becomes second nature, although the process may appear rather strange
and complicated at first sight.
We begin by showing you how to multiply a row vector by a column vector. To illustrate
this let us suppose that goods G1, G2 and G3 sell at $50, $30 and $20, respectively, and let us
introduce the row vector
p = [50 30 20]
If the firm sells a total of 100, 200 and 175 goods of type G1, G2 and G3, respectively, then we
can write this information as the column vector
q =
The total revenue received from the sale of G1 is found by multiplying the price, $50, by the
quantity, 100, to get
$50 × 100 = $5000
Similarly, the revenue from G2 and G3 is
$30 × 200 = $6000
and
20 × 175 = $3500
respectively. The total revenue of the firm is therefore
TR = $5000 + $6000 + $3500 = $14 500
The value of TR is a single number and can be regarded as a 1 × 1 matrix: that is,
[14 500]
This 1 × 1 matrix is obtained by multiplying together the price vector, p, and the quantity
vector, q, to get
[50 30 20] = [14 500]
The value 14 500 is found by multiplying the corresponding elements of p and q and then
adding together: that is,
J
K
K
L
100
200
175
G
H
H
I
J
K
K
L
100
200
175
G
H
H
I
MFE_C07a.qxd 16/12/2005 10:45 Page 461

In general, if a is the row vector
[a
11
a
12
a
13
... a
1s
]
and b is the column vector
then we define the matrix product
ab = [a
11
a
12
a
13
... a
1s
]
to be the 1 × 1 matrix
[a
11
b
11
+ a
12
b
21
+ a
13
b
31
+ ... + a
1s
b
s1
]
It is important to notice that the single element in the 1 × 1 matrix ab is found by multiplying
each element of a by the corresponding element of b. Consequently, it is essential that both
vectors have the same number of elements. In other words, if a has order 1 × s and b has order
t × 1 then it is only possible to form the product ab when s = t.
J
K
K
K
K
K
K
L
b
11
b
21
b
31
.
.
.
b
s1
G
H
H
H
H
H
H
I
J
K
K
K
K
K
K
L
b
11
b
21
b
31
.
.
.
b
s1
G
H
H
H
H
H
H
I
Matrices
462
Example
If
a = [1234],b = and c =
find ab and ac.
Solution
Using the definition of the multiplication of a row vector, by a column vector, we have
ab = [1234] = [1(2) + 2(5) + 3(−1) + 4(0)] = [9]
J
K
K
K
K
L
2
5
−1
0
G
H
H
H
H
I
J
K
K
L
6
9
2
G
H
H
I
J
K
K
K
K
L
2
5
−1
0
G
H
H
H
H
I
MFE_C07a.qxd 16/12/2005 10:45 Page 462

We have set out the calculations in this way so that you can see how the value, 9, is obtained. There is no
need for you to indicate this in your own answers and you may simply write
[1234] = [9]
without bothering to insert any intermediate steps.
It is impossible to multiply a and c because a has four elements and c has only three elements. You can
see the problem if you actually try to perform the calculations, since there is no entry in c with which to mul-
tiply the 4 in a.
[1234] = [1(6) + 2(9) + 3(2) + 4(?)]
J
K
K
L
6
9
2
G
H
H
I
J
K
K
K
K
L
2
5
−1
0
G
H
H
H
H
I
7.1 • Basic matrix operations
463
Example
Find AB in the case when
A = and B =
J
K
K
L
3121
1012
5411
G
H
H
I
J
K
L
21 0
10 4
G
H
I
Practice Problem
5 Let
a = [1 −1032],b = [1 2 9], c = and d =
Find (where possible)
(a)
ac (b) bd (c) ad
J
K
K
K
K
K
K
L
0
−1
1
1
2
G
H
H
H
H
H
H
I
J
K
K
L
−2
1
0
G
H
H
I
We now turn our attention to general matrix multiplication, which is defined as follows. If
A is an m × s matrix and B is an s × n matrix then
C = AB
is an m × n matrix and c
ij
is found by multiplying the ith row of A into the jth column of B.
There are three things to notice about this definition. Firstly, the number of columns of A is
the same as the number of rows of B. Unless this condition is satisfied it is impossible to form the
product AB. Secondly, the matrix C has order m × n, where m is the number of rows of A and
n is the number of columns of B. Finally, the elements of C are found by multiplying row vectors
by column vectors. The best way of understanding this definition is to consider an example.
MFE_C07a.qxd 16/12/2005 10:45 Page 463
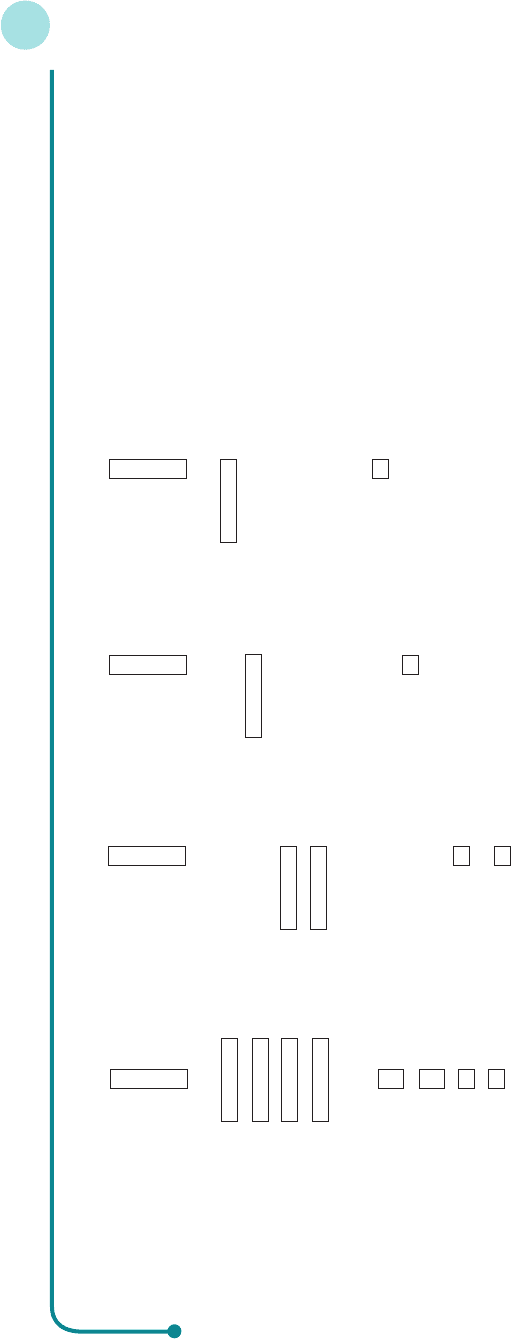
Solution
It is a good idea to check before you begin any detailed calculations that it is possible to multiply these
matrices and also to identify the order of the resulting matrix. In this case
A is a 2 × 3 matrix and B is a 3 × 4 matrix
Matrix A has three columns and B has the same number of rows, so it is possible to find AB. Moreover, AB
must have order 2 × 4 because A has two rows and B has four columns. Hence
=
All that remains for us to do is to calculate the eight numbers c
ij
.
The number c
11
in the top left-hand corner lies in the first row and first column, so to find its value we
multiply the first row of A into the first column of B to get
=
because 2(3) + 1(1) + 0(5) = 7.
The number c
12
lies in the first row and second column, so to find its value we multiply the first row of
A into the second column of B to get
=
because 2(1) + 1(0) + 0(4) = 2.
The values of c
13
and c
14
are then found in a similar way by multiplying the first row of A into the third
and fourth columns of B, respectively, to get
=
because 2(2) + 1(1) + 0(1) = 5 and 2(1) + 1(2) + 0(1) = 4.
Finally, we repeat the whole procedure along the second row of C. The elements c
21
, c
22
, c
23
and c
24
are
calculated by multiplying the second row of A into the four columns of B in succession to get
=
because
1(3) + 0(1) + 4(5) = 23
1(1) + 0(0) + 4(4) = 17
1(2) + 0(1) + 4(1) = 6
1(1) + 0(2) + 4(1) = 5
J
K
L
7254
23 17 6 5
G
H
I
J
K
K
L
3121
1012
5411
G
H
H
I
J
K
L
210
104
G
H
I
J
K
L
7254
c
21
c
22
c
23
c
24
G
H
I
J
K
K
L
3121
1012
5411
G
H
H
I
J
K
L
210
104
G
H
I
J
K
L
72c
13
c
14
c
21
c
22
c
23
c
24
G
H
I
J
K
K
L
3121
1012
5411
G
H
H
I
J
K
L
210
104
G
H
I
J
K
L
7 c
12
c
13
c
14
c
21
c
22
c
23
c
24
G
H
I
J
K
K
L
3121
1012
5411
G
H
H
I
J
K
L
210
104
G
H
I
J
K
L
c
11
c
12
c
13
c
14
c
21
c
22
c
23
c
24
G
H
I
J
K
K
L
3121
1012
5411
G
H
H
I
J
K
L
210
104
G
H
I
Matrices
464
MFE_C07a.qxd 16/12/2005 10:45 Page 464
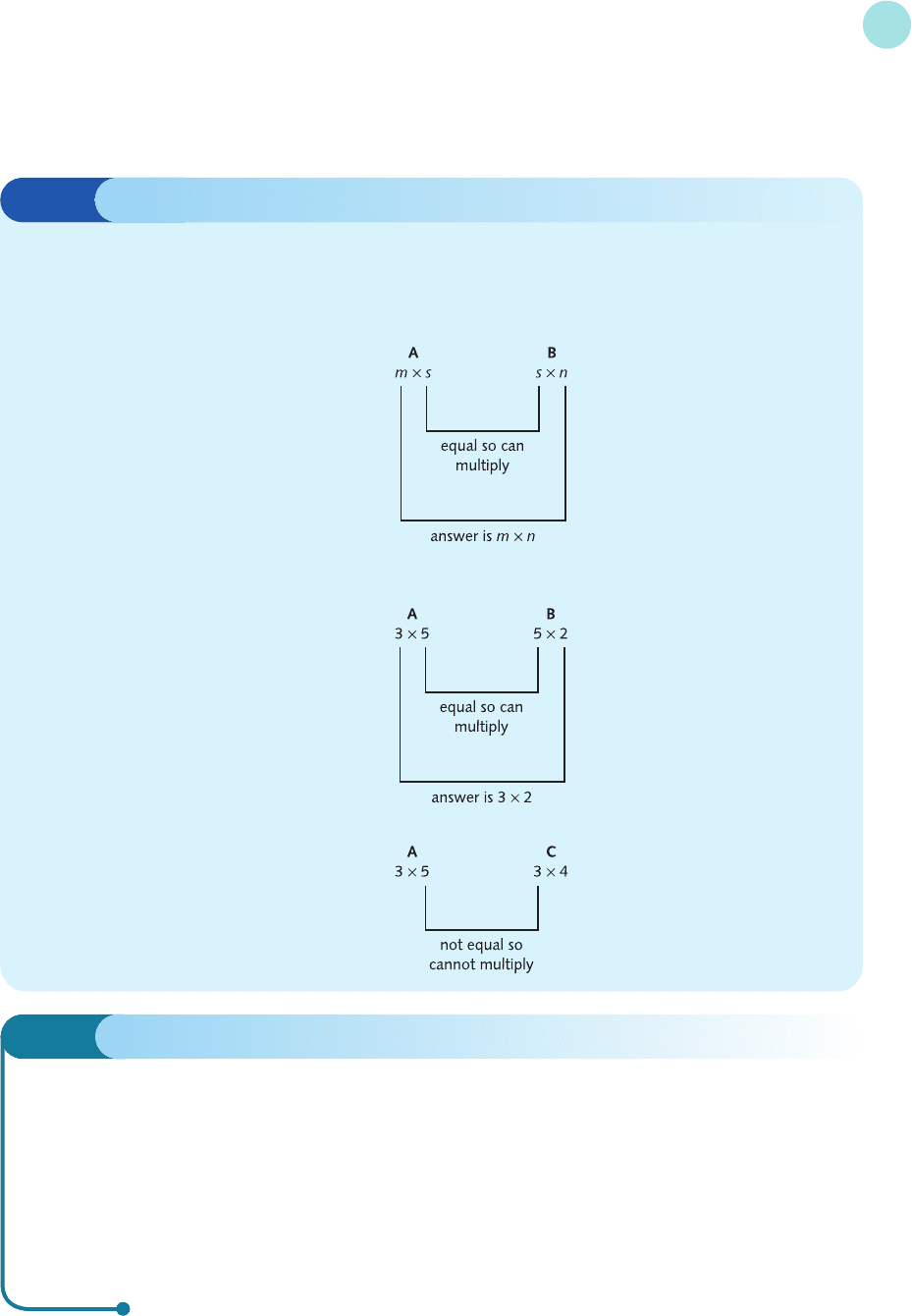
In this example we have indicated how to build up the matrix C in a step-by-step manner
and have used boxes to show you how the calculations are performed. This approach has been
adopted merely as a teaching device. There is no need for you to set your calculations out in
this way and you are encouraged to write down your answer in a single line of working.
7.1 • Basic matrix operations
465
Advice
Take the trouble to check before you begin that it is possible to form the matrix product
and to anticipate the order of the end result. This can be done by jotting down the orders
of the original matrices side by side. The product exists if the inner numbers are the same
and the order of the answer is given by the outer numbers: that is,
For example, if A, B and C have orders 3 × 5, 5 × 2 and 3 × 4 respectively, then AB exists
and has order 3 × 2 because
but it is impossible to form AC because
Practice Problem
6 Write down the order of the matrices
A = and B =
Hence verify that it is possible to form the matrix product
C = AB
and write down the order of C. Calculate all of the elements of C.
J
K
L
12
34
G
H
I
J
K
K
L
12
01
31
G
H
H
I
MFE_C07a.qxd 16/12/2005 10:45 Page 465

We have already noted that matrix operations have similar properties to those of ordinary
arithmetic. Some particular rules of arithmetic are:
a(b + c) = ab + ac (distributive law)
(a + b)c = ac + bc (distributive law)
a(bc) = (ab)c (associative law)
ab = ba (commutative law)
An obvious question to ask is whether they have a counterpart in matrix algebra. It turns out
that provided the matrices A, B and C have the correct orders for the appropriate sums and
products to exist then
A(B + C) = AB + AC
(A + B)C = AC + BC
A(BC) = (AB)C
However, although it is true that
ab = ba
for numbers, this result does not extend to matrices. Even if AB and BA both exist it is not
necessarily true that
AB = BA
This is illustrated in the following example.
Matrices
466
Example
If
A = and B =
evaluate AB and BA.
Solution
It is easy to check that it is possible to form both products AB and BA and that they both have order 2 × 2.
In fact
AB ==
BA ==
so AB ≠ BA.
J
K
L
72
51
G
H
I
J
K
L
1 −1
21
G
H
I
J
K
L
13
12
G
H
I
J
K
L
01
38
G
H
I
J
K
L
13
12
G
H
I
J
K
L
1 −1
21
G
H
I
J
K
L
13
12
G
H
I
J
K
L
1 −1
21
G
H
I
There are certain pairs of matrices which do commute (that is, for which AB = BA) and we
shall investigate some of these in the next section. However, these are very much the exception.
We therefore have the ‘non-property’ that, in general,
AB ≠ BA
MFE_C07a.qxd 16/12/2005 10:45 Page 466

We conclude this section by showing you how to express a familiar problem in matrix nota-
tion. Section 1.2 described the method of elimination for solving systems of simultaneous lin-
ear equations. For example, we might want to find values of x and y which satisfy
2x − 5y = 6
7x + 8y =−1
Motivated by the result of Problem 8 we write this as
Ax = b
where
A = x = b =
It is easy to check that this is correct simply by multiplying out Ax to get
=
and so the matrix equation Ax = b reads
=
J
K
L
6
−1
G
H
I
J
K
L
2x − 5y
7x + 8y
G
H
I
J
K
L
2x − 5y
7x + 8y
G
H
I
J
K
L
x
y
G
H
I
J
K
L
2 −5
78
G
H
I
J
K
L
6
−1
G
H
I
J
K
L
x
y
G
H
I
J
K
L
2 −5
78
G
H
I
7.1 • Basic matrix operations
467
Practice Problems
7 Let
A = B = C = D = and E =
Find (where possible)
(a)
AB (b) BA (c) CD (d) DC
(e) AE (f) EA (g) DE (h) ED
8 Evaluate the matrix product Ax, where
A = and x =
Hence show that the system of linear equations
x + 4y + 7z =−3
2x + 6y + 5z = 10
8x + 9y + 5z = 1
can be written as Ax = b where
b =
J
K
K
L
−3
10
1
G
H
H
I
J
K
K
L
x
y
z
G
H
H
I
J
K
K
L
147
265
895
G
H
H
I
J
K
L
123
456
G
H
I
J
K
K
L
11
−11
21
G
H
H
I
J
K
L
12
31
G
H
I
J
K
K
L
1
2
1
G
H
H
I
J
K
K
L
211
510
−114
G
H
H
I
MFE_C07a.qxd 16/12/2005 10:45 Page 467
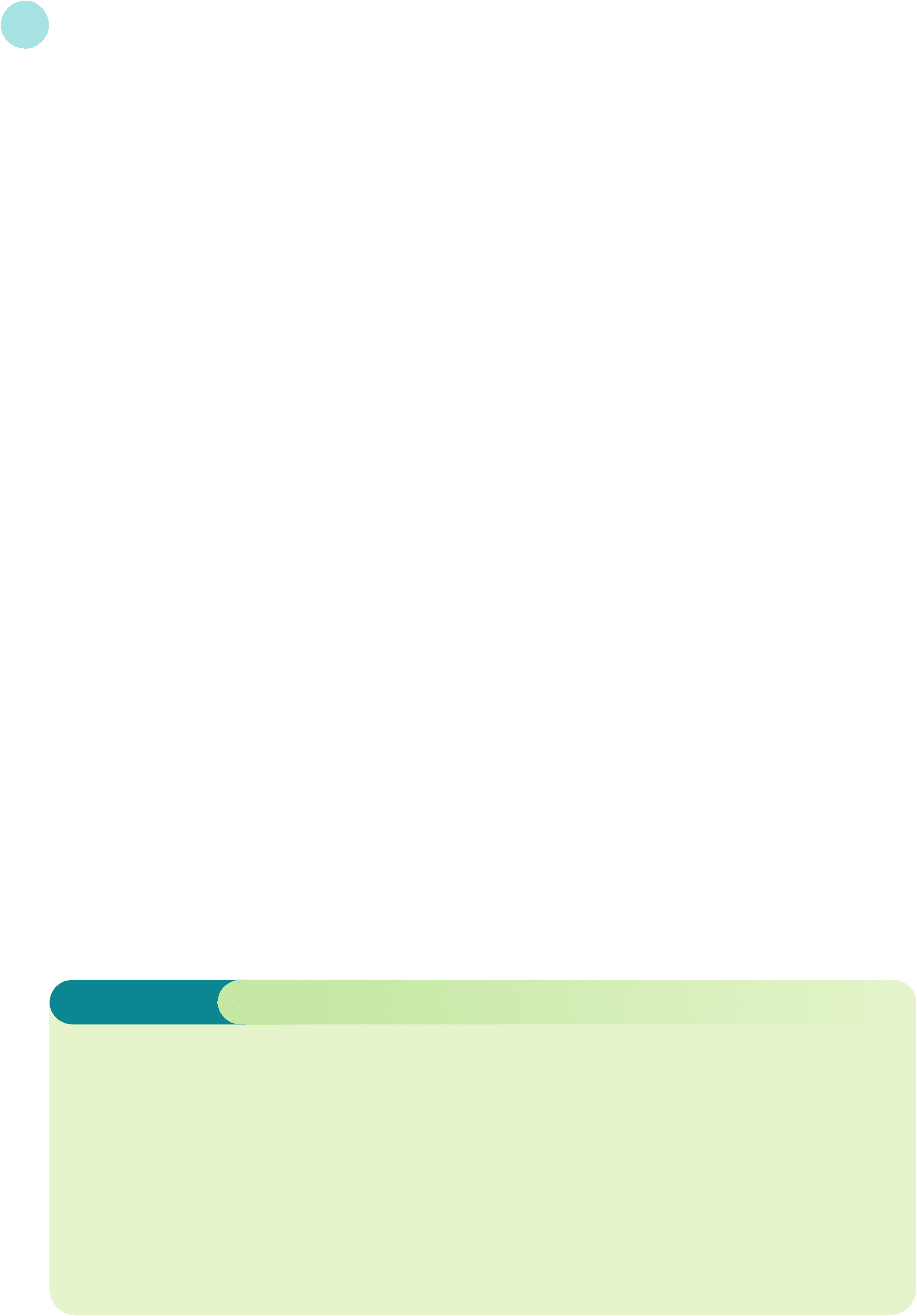
that is,
2x − 5y = 6
7x + 8y =−1
Quite generally, any system of n linear equations in n unknowns can be written as
Ax = b
where A, x and b are n × n, n × 1 and n × 1 matrices respectively. The matrix A consists of the
coefficients, the vector x consists of the unknowns and the vector b consists of the right-hand
sides. The definition of matrix multiplication allows us to write a linear system in terms of
matrices, although it is not immediately obvious that there is any advantage in doing so. In the
next section we introduce the concept of a matrix inverse and show you how to use this to solve
systems of equations expressed in matrix form.
Throughout this section we have noted various properties that matrices satisfy. For conveni-
ence these are summarized in the next subsection.
7.1.5 Summary
Provided that the indicated sums and products make sense,
A + B = B + A
A − A = 0
A + 0 = A
k(A + B) = kA + kB
k(lA) = (kl )A
A(B + C) = AB + AC
(A + B)C = AC + BC
A(BC) = (AB)C
We also have the non-property that, in general,
AB ≠ BA
Matrices
468
Column vector A matrix with one column.
Elements The individual numbers inside a matrix. (Also called entries.)
Matrix A rectangular array of numbers, set out in rows and columns, surrounded by a pair
of brackets. (Plural matrices.)
Order The dimensions of a matrix. A matrix with m rows and n columns has order m × n.
Row vector A matrix with one row.
Transpose of a matrix The matrix obtained from a given matrix by interchanging rows
and columns. The transpose of a matrix A is written A
T
.
Zero matrix A matrix in which every element is zero.
Key Terms
MFE_C07a.qxd 16/12/2005 10:45 Page 468

7.1 • Basic matrix operations
469
Practice Problems
9 The monthly sales (in thousands) of burgers (B1) and bites (B2) in three fast-food restaurants
(R1, R2, R3) are as follows:
R1 R2 R3
B1 35 27 13
B2 42 39 24
January
R1 R2 R3
B1 31 17 3
B2 25 29 16
February
(a) Write down two 2 × 3 matrices J and F
representing sales in January and February
respectively.
(b) By finding J + F, write down the matrix for the
total sales over the two months.
(c) By finding J − F, write down the matrix for the
difference in sales for the two months.
10 If
A = B =
work out
(a) 2A (b) 2B (c) 2A + 2B (d) 2(A + B)
Do you notice any connection between your answers to parts (c) and (d)?
11 A firm manufactures three products, P1, P2 and P3, which it sells to two customers, C1 and C2. The
number of items of each product that are sold to these customers is given by
P1 P2 P3
A = C1
C2
J
K
L
679
212
G
H
I
J
K
K
L
1796
2105
6453
G
H
H
I
J
K
K
L
2319
1050
6784
G
H
H
I
Advice
There now follow some Practice Problems. If you find that you do not have time to do all
of them, you should at least attempt Practice Problem 15 because the result of this prob-
lem will be used in the next section.
MFE_C07a.qxd 16/12/2005 10:45 Page 469
