Jackson S.L. Research Methods and Statistics: A Critical Thinking Approach
Подождите немного. Документ загружается.


252
■ ■
CHAPTER 9
CHAPTER 9 SUMMARY AND REVIEW: INFERENTIAL STATISTICS: TWO-GROUP DESIGNS
Several inferential statistics used with two-group
designs were discussed in this chapter. The statistics
varied based on the type of data collected (nomi-
nal, ordinal, interval-ratio) and whether the design
was between-participants or correlated-groups. It is
imperative that the appropriate statistic be used to
analyze the data collected in an experiment. The first
point to consider when determining which statistic to
use is whether it should be a parametric or nonpara-
metric statistic. This decision is based on the type of
data collected, the type of distribution to which the
data conform, and whether any parameters of the
distribution are known. Second, we need to know
whether the design is between-participants or cor-
related-groups when selecting a statistic. Using this
information, you can select and conduct the statistical
test most appropriate to the design and data.
Chapter 9
■
Study Guide
CHAPTER NINE REVIEW EXERCISES
(Answers to exercises appear in Appendix C.)
FILL-IN SELF TEST
Answer the following questions. If you have trouble
answering any of the questions, restudy the relevant
material before going on to the multiple-choice self
test.
1. A(n)
is a parametric inferential
test for comparing sample means of two inde-
pendent groups of scores.
2.
is an inferential statistic for
measuring effect size with t tests.
3. A(n)
is a parametric inferential
test used to compare the means of two related
samples.
4. When using a correlated-groups t test, we
calculate
, scores representing
the difference between participants’ performance
in one condition and their performance in a sec-
ond condition.
5. The standard deviation of the sampling distri-
bution of mean differences between dependent
samples in a two-group experiment is the
.
6. and frequen-
cies are used in the calculation of the
2
statistic.
7. The nonparametric inferential statistic for
comparing two groups of different peo-
ple when ordinal data are collected is the
.
8. When frequency data are collected, we use
the
to determine how well
an observed frequency distribution of two
nominal variables fits some expected breakdown.
9. Effect size for a chi-square test is determined by
using the
.
10. The Wilcoxon
test is used with
within-participants designs.
11. The Wilcoxon rank-sum test is used with
designs.
12. Chi-square tests use
data,
whereas Wilcoxon tests use
data.
10017_09_ch9_p225-255.indd 252 2/1/08 1:28:57 PM
Inferential Statistics: Two-Group Designs
■ ■
253
MULTIPLE-CHOICE SELF TEST
Select the single best answer for each of the following
questions. If you have trouble answering any of the
questions, restudy the relevant material.
1. When comparing the sample means for two unre-
lated groups we use the:
a. correlated-groups t test.
b. independent-groups t test.
c. Wilcoxon rank-sum test.
d.
2
test of independence.
2. The value of the t test will
as sample
variance decreases.
a. increase
b. decrease
c. stay the same
d. not be affected
3. Which of the following t test results has the great-
est chance of statistical significance?
a. t(28) = 3.12
b. t(14) = 3.12
c. t(18) = 3.12
d. t(10) = 3.12
4. If the null hypothesis is false, then the t test
should be:
a. equal to 0.00.
b. greater than 1.
c. greater than .05.
d. greater than .95.
5. Imagine that you conducted an independent-
groups t test with 10 participants in each group.
For a one-tailed test, the t
cv
at .05 would be:
a. ±1.729.
b. ±2.101.
c. ±1.734.
d. ±2.093.
6. If a researcher reported for an independent-
groups t test that t(26) = 2.90, p .005, how many
participants were there in the study?
a. 13
b. 26
c. 27
d. 28
7. H
a
:
1
2
is the hypothesis for a
-tailed test.
a. null; two
b. alternative; two
c. null; one
d. alternative; one
8. Cohen’s d is a measure of for a .
a. significance; t test
b. significance;
2
test
c. effect size; t test
d. effect size;
2
test
9. t
cv
2.15 and t
obt
2.20. Based on these results
we:
a. reject H
0
.
b. fail to reject H
0
.
c. accept H
0
.
d. reject H
a
.
10. If a correlated-groups t test and an independent-
groups t test both have df 10, which experiment
used fewer participants?
a. both used the same number of participants
(n 10)
b. both used the same number of participants
(n 11)
c. the correlated-groups t test
d. the independent-groups t test
11. If researchers reported that, for a correlated-
groups design, t(15) = 2.57, p .05, you can
conclude that:
a. a total of 16 people participated in the study.
b. a total of 17 people participated in the study.
c. a total of 30 people participated in the study.
d. there is no way to determine how many
people participated in the study.
12. Error variance due to
is when
using the correlated-groups t test.
a. the independent variable; decreased
b. the independent variable; increased
c. individual difference; increased.
d. individual differences; decreased
13. Parametric is to nonparametric as
is to
.
a. z test; t test
b. t test; z test
c.
2
test; z test
d. t test;
2
test
14. Which of the following is an assumption of
2
tests?
a. It is a parametric test.
b. It is appropriate only for ordinal data.
c. The frequency in each expected cell should be
less than 5.
d. The sample should be randomly selected.
10017_09_ch9_p225-255.indd 253 2/1/08 1:28:58 PM

254
■ ■
CHAPTER 9
15. The calculation of the df for the is
(r 1)(c 1).
a. independent-groups t test
b. correlated-groups t test
c.
2
test of independence
d. Wilcoxon rank-sum test
16. The
is a measure of effect size for the
.
a. phi coefficient;
2
goodness-of-fit test
b. eta-squared;
2
goodness-of-fit test
c. phi coefficient;
2
test of independence
d. eta-squared; Wilcoxon rank-sum test
17. The Wilcoxon rank-sum test is used with
data.
a. interval
b. ordinal
c. nominal
d. ratio
18. Wilcoxon rank-sum test is to
design as
Wilcoxon matched-pairs signed-ranks T test is to
design.
a. between-participants; within-participants
b. correlated-groups; within-participants
c. correlated-groups; between-participants
d. within-participants; matched-participants
SELF-TEST PROBLEMS
1. A college student is interested in whether there is
a difference between male and female students in
the amount of time spent doing volunteer work
each week. The student gathers information from
a random sample of male and female students
on her campus. Amount of time volunteering (in
minutes) is normally distributed. The data appear
next. They are measured on an interval-ratio scale
and are normally distributed.
Males Females
20 35
25 39
35 38
40 43
36 50
24 49
a. What statistical test should be used to analyze
these data?
b. Identify H
0
and H
a
for this study.
c. Conduct the appropriate analysis.
d. Should H
0
be rejected? What should the
researcher conclude?
e. If significant, compute and interpret the effect
size.
f. If significant, draw a graph representing the
data.
g. Calculate the 95% confidence interval.
2. A researcher is interested in whether studying
with music helps or hinders the learner. To control
for differences in cognitive ability, the researcher
decides to use a within-participants design. He
selects a random sample of participants and has
them study different material of equal difficulty
in both the music and no music conditions.
Participants then take a 20-item quiz on the mate-
rial. The study is completely counterbalanced to
control for order effects. The data appear next.
They are measured on an interval-ratio scale and
are normally distributed.
Music No Music
17 17
16 18
15 17
16 17
18 19
18 18
a. What statistical test should be used to analyze
these data?
b. Identify H
0
and H
a
for this study.
c. Conduct the appropriate analysis.
d. Should H
0
be rejected? What should the
researcher conclude?
e. If significant, draw a graph representing the
data.
g. Calculate the 95% confidence interval.
3. Researchers at a food company are interested
in how a new ketchup made from green toma-
toes (and green in color) will compare to their
traditional red ketchup. They are worried that
the green color will adversely affect the tasti-
ness scores. They randomly assign participants
to either the green or red ketchup condition.
Participants indicate the tastiness of the sauce
10017_09_ch9_p225-255.indd 254 2/1/08 1:28:58 PM

Inferential Statistics: Two-Group Designs
■ ■
255
on a 20-point scale. Tastiness scores tend to be
skewed. The scores follow.
Green Ketchup Red Ketchup
14 16
15 16
16 19
18 20
16 17
16 17
19 18
a. What statistical test should be used to analyze
these data?
b. Identify H
0
and H
a
for this study.
c. Conduct the appropriate analysis.
d. Should H
0
be rejected? What should the
researcher conclude?
4. You notice at the gym that it appears that more
women tend to work out together, whereas
more men tend to work out alone. To determine
whether this difference is significant, you collect
data on the workout preferences for a sample of
men and women at your gym. The data follow.
Males Females
Together 12 24
Alone 22 10
a. What statistical test should be used to analyze
these data?
b. Identify H
0
and H
a
for this study.
c. Conduct the appropriate analysis.
d. Should H
0
be rejected? What should the
researcher conclude?
10017_09_ch9_p225-255.indd 255 2/1/08 1:28:59 PM

256
Experimental Designs with
More Than Two Levels of
an Independent Variable
10
CHAPTER
Using Designs with More Than Two Levels of an Independent Variable
Comparing More Than Two Kinds of Treatment in One Study
Comparing Two or More Kinds of Treatment with the Control Group (No Treatment)
Comparing a Placebo Group with the Control and Experimental Groups
Analyzing the Multiple-Group Experiment Using Parametric Statistics
Between-Participants Designs: One-Way Randomized ANOVA
One-Way Randomized ANOVA: What It Is and What It Does • Calculations
for the One-Way Randomized ANOVA • Interpreting the One-Way Randomized
ANOVA • Graphing the Means and Effect Size • Assumptions of the One-Way
Randomized ANOVA • Tukey’s Post Hoc Test
Correlated-Groups Designs: One-Way Repeated Measures ANOVA
One-Way Repeated Measures ANOVA: What It Is and What It Does • Calculations
for the One-Way Repeated Measures ANOVA • Interpreting the One-Way Repeated
Measures ANOVA • Graphing the Means and Effect Size • Assumptions of the
One-Way Repeated Measures ANOVA • Tukey’s Post Hoc Test
Nonparametric Statistics for the Multiple-Group Experiment
Summary
10017_10_ch10_p256-289.indd 256 2/1/08 1:30:25 PM
Experimental Designs with More Than Two Levels of an Independent Variable
■ ■
257
Learning Objectives
• Explain what additional information can be gained by using designs
with more than two levels of an independent variable.
• Identify what a one-way randomized ANOVA is and what it does.
• Use the formulas provided to calculate a one-way randomized ANOVA.
• Interpret the results from a one-way randomized ANOVA.
• Calculate Tukey’s post hoc test for a one-way randomized ANOVA.
• Identify what a one-way repeated measures ANOVA is and what it
does.
• Use the formulas provided to calculate a one-way repeated measures
ANOVA.
• Interpret the results from a one-way repeated measures ANOVA.
• Calculate Tukey’s post hoc test for a one-way repeated measures
ANOVA.
T
he experiments described in Chapter 8 involved manipulating one
independent variable with only two levels—either a control group
and an experimental group or two experimental groups. In this
chapter, we will discuss experimental designs that involve one independent
variable with more than two levels. Examining more levels of an independ-
ent variable allows us to address more complicated and interesting ques-
tions. Often experiments begin as two-group designs and then develop into
more complex designs as the questions asked become more elaborate and
sophisticated. The same design principles presented in Chapter 8 also apply
to these more complex designs; that is, we still need to be concerned about
control, internal validity, and external validity.
Using Designs with More Than Two Levels
of an Independent Variable
Researchers may decide to use a design with more than two levels of an
independent variable for three reasons. First, it allows them to compare
multiple treatments. Second, it enables them to compare multiple treat-
ments with no treatment (the control group). Third, more complex designs
allow researchers to compare a placebo group with control and experimental
groups (Mitchell & Jolley, 2004).
Comparing More Than Two Kinds
of Treatment in One Study
To illustrate this advantage of more complex experimental designs, imagine
that we want to compare the effects of various types of rehearsal on memory.
We have participants study a list of 10 words using either rote rehearsal
10017_10_ch10_p256-289.indd 257 2/1/08 1:30:26 PM
258
■ ■
CHAPTER 10
(repetition) or some form of elaborative rehearsal. In addition, we specify the
type of elaborative rehearsal to be used in the different experimental groups.
Group 1 (the control group) uses rote rehearsal, group 2 uses an imagery
mnemonic technique, and group 3 uses a story mnemonic device. You may
be wondering why we don’t simply conduct three studies or comparisons.
Why don’t we compare group 1 to group 2, group 2 to group 3, and group
1 to group 3 in three different experiments? There are several reasons this is
not recommended.
You may remember from Chapter 9 that a t test is used to compare per-
formance between two groups. If we do three experiments, we need to use
three t tests to determine these differences. The problem is that using multi-
ple tests inflates the Type I error rate. Remember, a Type I error means that
we reject the null hypothesis when we should have failed to reject it; that is,
we claim that the independent variable has an effect when it does not. For
most statistical tests, we use the .05 alpha level, meaning that we are willing
to accept a 5% risk of making a Type I error. Although the chance of making
a Type I error on one t test is .05, the overall chance of making a Type I error
increases as more tests are conducted.
Imagine that we conducted three t tests or comparisons among the three
groups in the memory experiment. The probability of a Type I error on any
single comparison is .05. The probability of a Type I error on at least one of
the three tests, however, is considerably higher. To determine the chance
of a Type I error when making multiple comparisons, we use the formula
1 – (1 )
c
, where c equals the number of comparisons performed. Using
this formula for the present example, we get the following:
1(1.05)
3
1(.95)
3
1.86 .14
Thus, the probability of a Type I error on at least one of the three tests is .14,
or 14%.
One way of counteracting the increased chance of a Type I error is to
use a more stringent alpha level. The Bonferroni adjustment, in which the
desired alpha level is divided by the number of tests or comparisons, is
typically used to accomplish this. For example, if we were using the t test to
make the three comparisons described previously, we would divide .05 by 3
and get .017. By not accepting the result as significant unless the alpha level
is .017 or less, we minimize the chance of a Type I error when making multi-
ple comparisons. We know from discussions in previous chapters, however,
that although using a more stringent alpha level decreases the chance of a
Type I error, it increases the chance of a Type II error (failing to reject the null
hypothesis when it should have been rejected—missing an effect of an inde-
pendent variable). Thus, the Bonferroni adjustment is not the best method of
handling the problem. A better method is to use a single statistical test that
compares all groups rather than using multiple comparisons and statistical
tests. Luckily for us, there is a statistical technique that will do this—the
analysis of variance (ANOVA), which will be discussed shortly.
Another advantage of comparing more than two kinds of treatment in
one experiment is that it reduces both the number of experiments conducted
Bonferroni adjustment
Setting a more stringent alpha
level for multiple tests to
minimize Type I errors.
Bonferroni adjustment
Setting a more stringent alpha
level for multiple tests to
minimize Type I errors.
10017_10_ch10_p256-289.indd 258 2/1/08 1:30:27 PM
Experimental Designs with More Than Two Levels of an Independent Variable
■ ■
259
and the number of participants needed. Once again, refer to the three-group
memory experiment. If we do one comparison with three groups, we can
conduct only one experiment, and we need participants for only three
groups. If, however, we conduct three comparisons, each with two groups,
then we need to perform three experiments, and we need participants for six
groups or conditions.
Comparing Two or More Kinds of Treatment
with the Control Group (No Treatment)
Using more than two groups in an experiment also allows researchers to
determine whether each treatment is more or less effective than no treatment
(the control group). To illustrate this, imagine that we are interested in the
effects of aerobic exercise on anxiety. We hypothesize that the more aerobic
activity one engages in, the more anxiety will be reduced. We use a control
group that does not engage in any aerobic activity and a high aerobic activ-
ity group that engages in 50 minutes per day of aerobic activity—a simple
two-group design. Assume, however, that when using this design, we find
that both those in the control group and those in the experimental group
have high levels of anxiety at the end of the study—not what we expected
to find. How could a design with more than two groups provide more infor-
mation? Suppose we add another group to this study—a moderate aerobic
activity group (25 minutes per day)—and get the following results:
Control group High anxiety
Moderate aerobic activity Low anxiety
High aerobic activity High anxiety
Based on these data, we have a V-shaped function. Up to a certain point,
aerobic activity reduces anxiety. However, when the aerobic activity exceeds
a certain level, anxiety increases again. If we had conducted the original
study with only two groups, we would have missed this relationship and
erroneously concluded that there was no relationship between aerobic activ-
ity and anxiety. Using a design with multiple groups allows us to see more
of the relationship between the variables.
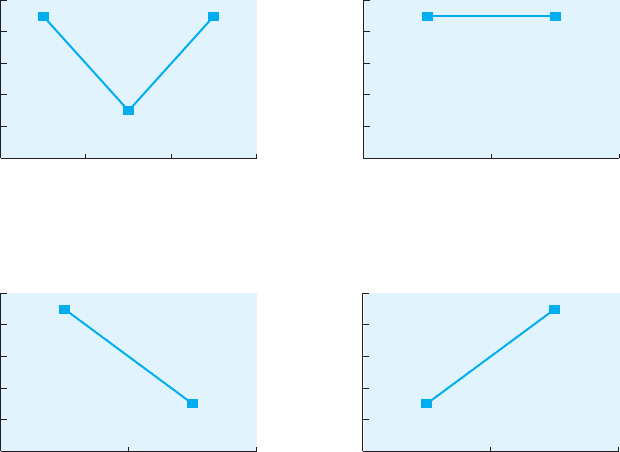
Figure 10.1 illustrates the difference between the results obtained with
the three-group and the two-group design in this hypothetical study. It also
shows the other two-group comparisons—control compared to moderate
aerobic activity, and moderate aerobic activity compared to high aerobic
activity. This set of graphs illustrates how two-group designs limit our abil-
ity to see the complete relationship between variables.
Figure 10.1a shows clearly how the three-group design allows us to
assess more fully the relationship between the variables. If we had con-
ducted only a two-group study, such as those illustrated in Figure 10.1b, c,
or d, we would have drawn a much different conclusion than that drawn
from the three-group design. Comparing only the control to the high
aerobic activity group (Figure 10.1b) would have led us to conclude that
aerobic activity does not affect anxiety. Comparing only the control and the
10017_10_ch10_p256-289.indd 259 2/1/08 1:30:27 PM
260
■ ■
CHAPTER 10
moderate aerobic activity group (Figure 10.1c) would have led to the con-
clusion that increasing aerobic activity reduces anxiety. Comparing only
the moderate aerobic activity group and the high aerobic activity group
(Figure 10.1d) would have led to the conclusion that increasing aerobic
activity increases anxiety.
Being able to assess the relationship between the variables means that we
can determine the type of relationship that exists. In the preceding example,
the variables produced a V-shaped function. Other variables may be related
in a straight linear manner or in an alternative curvilinear manner (for
example, a J-shaped or S-shaped function). In summary, adding levels to the
independent variable allows us to determine more accurately the type of
relationship that exists between the variables.
Comparing a Placebo Group with the Control
and Experimental Groups
A final advantage of designs with more than two groups is that they allow
for the use of a placebo group. How can adding a placebo group improve an
experiment? Consider an often-cited study by Paul (1966, 1967) involving
children who suffered from maladaptive anxiety in public speaking situations.
Paul used a control group, which received no treatment; a placebo group,
FIGURE 10.1
Determining r
ela-
tionships with
three-group versus
two-group designs:
(a) three-group
design; (b) two-
group comparison
of control to high
aerobic activity;
(c) two-group com-
parison of control
to moderate aerobic
activity; (d) two-
group comparison
of moderate aerobic
activity to high
aerobic activity
0
2
4
6
8
10
HighModerateControl
Anxiety
0
2
4
6
8
10
High
Control
Anxiety
0
2
4
6
8
10
Moderate
Control
Anxiety
Exercise Group
0
2
4
6
8
10
High
Moderate
Anxiety
Exercise Group
Exercise Group Exercise Group
cd
ab
10017_10_ch10_p256-289.indd 260 2/1/08 1:30:28 PM

Experimental Designs with More Than Two Levels of an Independent Variable
■ ■
261
which received a placebo that they were told was a potent tranquilizer; and
an experimental group, which received desensitization therapy. Of those in
the experimental group, 85% showed improvement, compared with only
22% in the control condition. If the placebo group had not been included, the
difference between the therapy and control groups (85% 22% 63%) would
overestimate the effectiveness of the desensitization program. The placebo
group showed 50% improvement, meaning that the therapy’s true effective-
ness is much less (85% 50% 35%). Thus, a placebo group allows for a
more accurate assessment of a therapy’s effectiveness because, in addition to
spontaneous remission, it controls for participant expectation effects.
Designs with More Than Two Levels of an Independent Variable IN REVIEW
ADVANTAGES CONSIDERATIONS
Allow comparisons of more than two types of treatment Type of statistical analysis (e.g., multiple t tests or
Require fewer participants ANOVA)
Allow comparisons of all treatments with control condition Multiple t tests increase chance of Type I error
Allow for use of a placebo group with control and Bonferroni adjustment increases chance of Type II
experimental groups error
CRITICAL
THINKING
CHECK
10.1
1. Imagine that a researcher wants to compare four different types of
treatment. The researcher decides to conduct six individual studies
to make these comparisons. What is the probability of a Type I error,
with alpha .05, across these six comparisons? Use the Bonferroni
adjustment to determine the suggested alpha level for these six tests.
Analyzing the Multiple-Group Experiment
Using Parametric Statistics
As noted previously, t tests are not recommended for comparing perform-
ance across groups in a multiple-group design because of the increased
probability of a Type I error. For multiple-group designs in which interval-
ratio data are collected, the recommended statistical analysis is the ANOVA
(analysis of variance)—an inferential parametric statistical test for compar-
ing the means of three or more groups. As its name indicates, this procedure
allows us to analyze the variance in a study. You should be familiar with
variance from Chapter 5 on descriptive statistics. Nonparametric analy-
ses are also available for designs in which ordinal data are collected (the
ANOVA (analysis of
variance) An inferential
statistical test for comparing the
means of three or more groups.
ANOVA (analysis of
variance) An inferential
statistical test for comparing the
means of three or more groups.
10017_10_ch10_p256-289.indd 261 2/1/08 1:30:28 PM
