Jackson S.D., Hargreaves J.S.J. Metal Oxide Catalysis

Подождите немного. Документ загружается.

2.2 Types of Electronic Transitions Producing UV-Vis-NIR Bands 53

In the following, the main features related to the nature of each type of electronic

transition and their dependence on the physical - chemical properties of the absorb-

ing/emitting systems are presented.

2.2.1

Metal - Centered Transitions

d → d transitions occur among the electron energy levels in incompletely ﬁ lled d

subshells (1 ≤ n ≤ 9), and so are typical for transition metal ions ( TMI ). The

number and relative position of such levels in TMI complexes (in solution, solid –

liquid interfaces [14] or in solid frameworks) results from the splitting of the free

ion terms by the ligand ﬁ eld, electron interactions (orbital, spin, spin – orbital

angular momentum coupling), conﬁ guration interactions and the Jahn – Teller

effect [15, 16] . These features in turn are controlled by the oxidation state of the

metal ions, the number and kind of ligands and the geometry of their arrangement

around the ions. Because all these dependences exist, the correct interpretation of

a d – d spectrum can yield relevant information about the nature of metal ions and

the composition and structure of the sites where they are hosted. In this respect,

effective, quantitative support is provided by the use of Orgel diagrams (from the

weak ﬁ eld method) and Tanabe – Sugano diagrams (from the strong ﬁ eld method)

[15 – 18] . Both of these allow the calculation of the crystal ﬁ eld parameter ∆

, which,

for given oxidation states and symmetry of the environment, depends on the

nature of the ligands, related to the spectrochemical series [15, 16] . In addition,

from Tanabe – Sugano diagrams, the value of the Racah parameter, B , for com-

plexed metal ions can be obtained. The ratio between B and the corresponding B

for free ions (available in the literature) results in the parameter β = B / B

, which

reﬂ ects the covalent character of the metal ion/ligand interaction, which has been

arranged in the nephelauxetic series. It may be of interest to note that once the

oxidation state and the symmetry are deﬁ ned, ∆

and B values can also be derived

by combining spectral data and qualitative d term energy levels reported in the

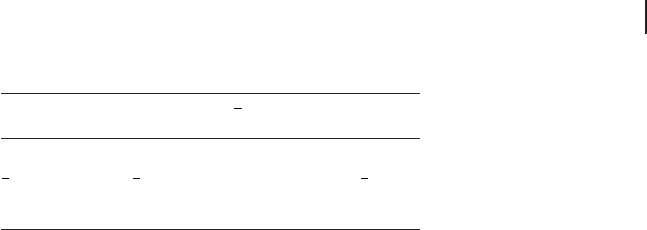
literature, such as those depicted in Figure 2.2 .

For instance, in the case of d

metal ions in a weak ligand environment

with an octahedral (or quasi - octahedral, such as C

) symmetry, ∆

and B

can be easily calculated on the basis of the position (e.g. in cm

− 1

) of ν

(

→

), ν

[

→

(F)] and ν

[

→

(P)] absorption bands,

Table 2.1 Conversion factors among wavelength λ (nm),

wavenumber ν (cm

− 1

), energy E (eV).

λ (nm)

(cm

− 1

) E (eV)

λ (nm)

(1/ λ ) ∤ 1 0

− 7

1240/ λ

(cm

− 1

) (1/

) ∤ 10

/8065.5

E (eV) 1240/E E ∤ 8065.5 1

54 2 The Application of UV-Visible-NIR Spectroscopy to Oxides

because the energy level scheme (right side) allows the determination of ∆

(= ν

) and B (= ( ν

+ ν

− 3 ν

)/15).

Normally, d – d transition bands are of weak intensity because they are forbidden

by the Laporte (orbital) selection rule (allowed transitions: ∆ l = ± 1; for systems

with inversion center: g → u or u → g). However, transitions that are forbidden

in octahedral symmetry may be partially allowed in the tetrahedral one, because

of d – p mixing in the t

orbital. Moreover, d – d transitions are subject to the spin -

selection rule which requires that spin multiplicity of the levels involved be the

same ( ∆ S = 0). However, neither the orbital nor the spin selection rules hold very

strictly, because of some relaxation afforded by vibronic coupling, spin – orbit cou-

pling or exchange interaction (in the case of polymetallic systems). Connected with

the relaxation of the Laporte rule by vibronic coupling is the phenomenon of

“ intensity stealing ” which can occur when a forbidden and a fully allowed transi-

tion involve excited terms close enough in energy to allow a mixing of the elec-

tronic wavefunctions, via a vibrational mode of proper symmetry. This is the

reason why certain d – d bands which lie close to charge - transfer (see below) bands

exhibit abnormally high intensity. Representative values of the intensity of d – d

bands in TMI complexes are listed in Table 2.2 .

Finally, for the sake of completeness, it must be considered that metal ions of

catalytic interest can exhibit absorption bands due to metal centered transitions of

other types, as summarized in Table 2.3 .

Figure 2.2 Weak ﬁ eld splitting scheme for maximum

multiplicity terms of d

ions in tetrahedral (left side) and

octahedral (right side) complexes. Adapted from ref. [17] .

2.2 Types of Electronic Transitions Producing UV-Vis-NIR Bands 55

2.2.2

Charge - Transfer ( CT ) Transitions

The intense color shown by several inorganic complexes, such as d

systems (e.g.

MnO

−

) in which no d – d transitions can occur, is due to transition between elec-

tronic states where the electron moves from one group of atoms to another [19] .

These charge - transfer ( CT ) transitions, which are Laporte allowed, produce very

intense bands, when the ∆ S = 0 selection rule is obeyed, and are sensitive to the

nature of both donor and acceptor atoms, to the local and general symmetry of

the absorbing centers and to their bonding geometry.

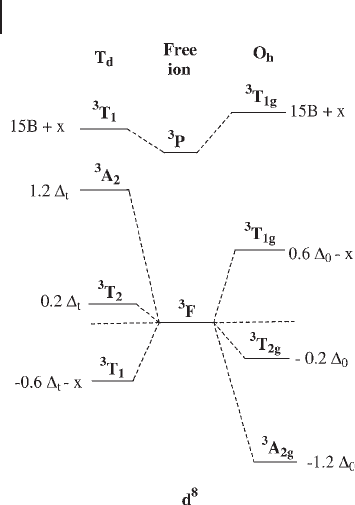
The main features of CT transitions are illustrated in Figure 2.3 . If the interac-

tion between the orbitals φ

and φ

(orbitals located on a single atom or groups of

atoms) is small, the new orbital φ

is composed mainly of φ

, and φ

is composed

mainly of φ

. In the case of MnO

−

the lower energy orbital φ

is located on the

oxygen ligands and φ

is a metal d orbital. The transition φ

→ φ

, called a ligand

to metal charge - transfer transition ( LMCT ), produces a decrease by 1 in the metal

oxidation state. In other systems, for instance metal carbonyls, where there are

high - lying empty ligand orbitals, φ

may be a metal d orbital and φ

a ligand orbital.

In this case, a metal to ligand charge - transfer transition ( MLCT ) occurs and pro-

duces an increase by 1 in the metal oxidation state. In fact, the charge transfer is

Table 2.2 Representative values for the intensities of d – d transitions in TMI complexes.

Type of d – d transition

Approximate e

Spin - forbidden, Laporte forbidden 0.1

Spin - allowed, Laporte forbidden 10

Spin - allowed, Laporte forbidden, with d – p mixing (tetrahedral symmetry) 100

Spin - allowed, Laporte forbidden, but with “ intensity stealing ” 1000

Table 2.3 Types of metal - centered transitions other than d – d.

Type of transition Comments Type of ions of

catalytic interest

f – f Laporte forbidden; slightly sensitive to the

surroundings; produce weak narrow bands

rare earth ions L

(e.g. Ce

)

( n − 1)d → n s

Laporte forbidden; often too high in energy to

produce bands below 200 nm

, Ag

(bands

in the UV - Vis)

( n − 1)f → n d

Laporte allowed Ce

, U

n s → n p

Laporte allowed Sn

, Sb

, Bi

56 2 The Application of UV-Visible-NIR Spectroscopy to Oxides

never complete and all electronic transitions involve a certain amount of electron

redistribution in the excited state compared with the ground state.

LMCT and MLCT transitions depend on the symmetry, on the oxidation state

of the metal and on the nature of the ligand or of the other metal atoms. In par-

ticular, the energy of CT transitions increases with the optical electronegativity

difference between the metal and the ligand [20 – 22] .

Optical electronegativity values ( χ

opt

) are assigned to elements in a given oxida-

tion state and Pauling electronegativity values for halide ions are used as refer-

ences. The wavenumber of the ﬁ rst CT absorption band is expressed as [23, 24]

χχχcm ligand metal

opt opt

−

()

−

()

[]

30000

(2.1)

CT transitions can involve metal ions in all electronic conﬁ gurations, and then,

as in the case of TMIs, are also responsible for optical bands for systems contain-

ing d

or d

TMIs, that, conversely, do not produce d – d absorption.

Intra - valence, or metal to metal, CT transitions can also occur within systems

containing ions of different oxidation state, as Fe

→ F e

in Fe

or Fe

→ T i

in sapphire [4] .

2.2.3

Transitions between Electron Energy Bands in Solids

The assembly of atoms into an array to form a solid leads to the formation of bands

of allowed states separated by an energy gap. This results from the fact that when

Figure 2.3 Schematic representation of CT transitions.

EA(A) = electron afﬁ nity of species A; IP(B) = ionization

potential of species B; ∆ = stabilization energy of AB.

Adapted from ref. [19] .

2.2 Types of Electronic Transitions Producing UV-Vis-NIR Bands 57

similar “ building blocks ” (atoms, unit cells) approach each other the wavefunc-

tions of their electrons start to overlap and, as a consequence of Pauli ’ s exclusion

principle, the energy states of all spin - paired electrons shared to form bonds are

slightly shifted from the original values when the building blocks are isolated. For

instance, by packing N building blocks the 2 N electrons originally occupying the

same orbital must be spread over 2 N different states, forming a band instead of

discrete levels. The distribution of the states so formed depends on the actual dis-

tance of the building blocks in the solids, leading to the appearance of a gap in

the energy band ( E

). The lower band, which can contain as many states as elec-

trons, and hence be completely ﬁ lled, is the valence band. The upper band, which

may contain no electrons at all or fewer electrons than states, is the conduction

band. The extent of the energy gap and the relative electron population determines

whether a solid is a metal, a semiconductor or an insulator. This last kind of mate-

rial has an E

larger than 3 eV and a negligible concentration of electrons in the

upper band (and practically no holes in the lower band). Semiconductors, however,

usually exhibit an E

lower than 3 eV and a density of electrons in the upper band

(or holes in the lower band) lower than 10

c m

− 3

. Promotion of electrons from the

valence to the conduction band (or to states localized in the gap) can occur by

absorption of energy from electromagnetic radiation, thus generating optical tran-

sitions. Finally, in metals, the conduction band is populated by electrons, with a

concentration of the order of 10

c m

− 3

A second fundamental aspect to be considered in relation to optical transitions

in solids, is that electron states, other than deﬁ nite energy assignments, are also

characterized by a distribution in the momentum space, related to the movement

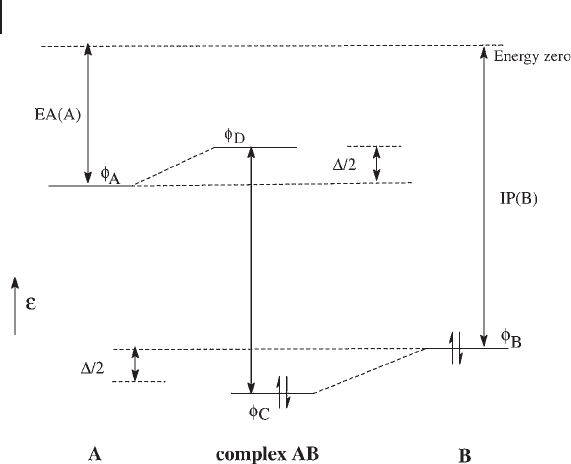
(i.e. to the kinetic energy) of electrons in the solid. For the sake of pictorial sim-

plicity, bidimensional models of crystals, conceived as a square well potential, are

usually employed in this respect, portraying the “ parabolic valley ” dependence (in

one direction) of energy from the “ momentum vector ” k , as schematized in Figure

2.4 A. The signiﬁ cance of the downward curvature of the valence band is that if

electrons could have a net motion in such a band (i.e. if it were not completely

ﬁ lled), they would be accelerated in the opposite direction with respect to those in

the conduction band.

It is important to note that in solids distances between nearest atoms can vary

in different directions, and hence the minimum of the valley may not occur at

= k

= 0, but at some point deﬁ ning a speciﬁ c direction, as shown in Figure

2.4 B for a crystalline solid. In an optical transition, both energy and momentum

must be conserved. Because the momentum of a photon, h / λ ( λ is the wavelength

of light which is typically thousands of å ngstr ö ms), is very small compared to the

crystal momentum h / a ( a is the lattice constant, typically a few Å ngstr ö ms), the

photon - absorption process should conserve the electron momentum.

Thus, the absorption coefﬁ cient α ( h ν ) for a given photon energy h ν is propor-

tional to the probability, P

, for the transition from the initial state to the ﬁ nal state

(governed also by the conservation of momentum), the density of electrons in the

initial state, n

, and also the density of electrons in the ﬁ nal states, n

. This process

must be summed for all possible transitions between states separated by an energy

difference equal to h ν :

58 2 The Application of UV-Visible-NIR Spectroscopy to Oxides

ανhAPnn

if i f

()

∑

(2.2)

Depending upon the relationship between the momentum in the initial and

ﬁ nal states (which, in turn, depend on the proﬁ le of the “ parabolic energy valley ” )

direct or indirect transitions can occur, as shown in Figure 2.4 , and this affects all

the three terms P

, n

and n

. It must be noted that in transitions between indirect

valleys (Figure 2.4 B) momentum is conserved via interaction with a phonon (i.e.

a quantum lattice vibration), which can be either emitted or adsorbed. Some addi-

tional detail on such transitions will be given in the section dealing with semicon-

ductor oxides.

By using the parabolic valley model, an expression of α ( h ν ) for each type of

transition (allowed or forbidden in dependence on selection rules) has been

obtained [25 – 27] . As a common feature, for crystalline solids, α ( h ν ) appeared

expressed in all cases in the form:

αν νhBhE

()

=−

()

(2.3)

where B contains the dependence on P

, n

and n

speciﬁ c for each type of transi-

tion (that essentially rules the transition edge width), E

is the interband energy

gap and n can take values 1/2, 3/2, 2, 3 for direct allowed, direct forbidden, indirect

allowed and indirect forbidden transitions, respectively. The value n = 2 holds for

amorphous materials also, irrespective of the type of transition found in corre-

sponding crystalline materials. Actually, the momentum vector is not conserved

in amorphous phases, and to obtain α ( h ν ) an integration over the density of states

must be made, as in the case of indirect transitions in crystalline systems.

A plot of [ α ( h ν )]

− n

against E ( h ν ) (values of the energy range the absorption edge

is spread over) should then result in a linear relationship, the intercept with the

Figure 2.4 Energy versus momentum and possible interband

transitions in: (A) a direct - gap two - band system and

(B) a solid with conduction band valleys at k = < 000 > and

k = < 111 > . Adapted from ref. [26] .

E ( h ν ) axis being E

. Examples of the use of this relation will be provided in the

section devoted to semiconductor oxides.

As a third point, it must be considered that when an electron is raised to the con-

duction band, it leaves behind an unoccupied state (a positive hole) in the valence

band. Thus the excited electron moves in the ﬁ eld of this positively charged hole,

and an e

−

pair forms which is called an exciton. A detailed discussion of such

kinds of states has been the subject of the work of Knox [28] . The binding energy

of such a couple slightly decreases the amount of energy required to cause an exci-

tonic transition with respect to a true valence to conduction one, where the excited

electron and the corresponding hole are free to move independently in the solids.

Hence, excitons generate electron states within the interband energy gap of a solid.

The binding energy of excitons depends on the effective e

−

and h

masses and the

dielectric constant of the solid. In semiconductors, such a dependence results in

very small binding energy, of the order of 0.01 eV. In solids of such type, excitons

exist in principle but will be completely ionized, the corresponding optical transi-

tions vanishing in the edge - shaped E

absorption. In a typical insulator, on the other

hand, effective masses are larger and the dielectric constant is signiﬁ cantly smaller

than in semiconductors. Ionized excitons cannot exist at room temperature (or at

higher temperatures), generating discrete bands at energy below the E

edge

absorption. Examples will be reported in the section devoted to insulating oxides.

2.3

UV - V is - NIR Absorption Spectroscopy

2.3.1

Theory of Diffuse Reﬂ ectance ( DR ) Spectroscopy

In the case of powdered catalysts, incident light is almost completely diffused and

it is necessary to use Diffuse Reﬂ ectance ( DR ) instead of transmission spectros-

copy. Mie theory can be applied to describe a single scattering of light which occurs

when light interacts with isotropic and non - interacting small particles. This theory

is not suitable for describing the optical properties of powders in which multiple

scattering occurs. In this case, it is necessary to use a phenomenological theory

that considers the absorbance and scattering coefﬁ cients. The Schuster – Kubelka –

Munk ( SKM ) model is widely accepted to describe matt surfaces [29] . The reﬂ ec-

tance of a solid includes specular reﬂ ectance and diffuse reﬂ ectance. This latter,

characterized by an angular distribution independent of the incident angle, pre-

vails in the case of powdered solids. Accordingly to the SKM approximation, the

diffuse reﬂ ectance of a layer of inﬁ nite thickness R

∞

is linked to the absorption K

and the scattering S coefﬁ cients by the expression:

KS FR R R=

()

=−

()()

∞∞∞

(2.4)

F ( R

∞

) is the remission, or SKM, function [29] .

2.3 UV-Vis-NIR Absorption Spectroscopy 59

60 2 The Application of UV-Visible-NIR Spectroscopy to Oxides

The reﬂ ectance depends upon the K / S ratio and not on the absolute values of

K and S . The scattering S coefﬁ cient is independent from the wavelength over

wide spectral ranges and therefore the SKM function reﬂ ects the trend of the

absorption K coefﬁ cient. Moreover, because SKM is a function of α ( h ν ), a plot of

( F ( R

∞

) h ν )

1/ n

against h ν can be used to determine E

in powdered semiconductor

oxides.

The SKM theory has some limitations and can be applied only when the follow-

ing experimental conditions are fulﬁ lled:

i) The incident radiation is monochromatic and completely diffused. The latter

condition can be obtained using samples with a high diffusion and low

absorption.

ii) The layer is of inﬁ nite thickness (generally obtained with a layer depth of

1 – 2 mm), to avoid loss of radiation by transmission.

iii) The absorption intensity is quite weak [ F ( R

∞

) ≤ 1].

iv) Photoluminescence is absent.

Moreover, diffuse reﬂ ectance depends on the particle sizes ( d ). When the particle

size decreases, the S coefﬁ cient increases since S ∝ 1 / d (for d ≥ 1 µ m) and this

results in an increase of reﬂ ectance. It is worth noting that in the case of thin ﬁ lms

(layers), the UV absorption spectra are complicated by the superposition of inter-

ference effects. The interference oscillations facilitate the semiquantitative deter-

mination of the layer thickness ( δ ), although they prevent the accurate determination

of the ﬁ lm absorption spectrum. In addition, a further uncertainty arises from

specular and diffuse reﬂ ectance by the ﬁ lm. It is possible to solve both problems

by measuring the transmittance ( T ) and reﬂ ectance ( R ) of the light in all directions

using the integrating sphere. The fraction of the truly absorbed light is (1 − R −

T ) and the plot of − ln( R + T ) against λ gives a spectrum in the scale of optical

densities. Since the reﬂ ected and transmitted beams are phase shifted by n δ ( n is

the refractive index), this type of plot is, moreover, smoothed by compensation of

the interference effects [30] .

Finally, it must be noted that an interesting consequence of the Kubelka – Munk

( KM ) equation is that DR spectroscopy has excellent properties for the analysis of

trace quantities of absorbing centers dispersed in non - absorbing matrices. As

shown in the following equation:

12 10

−

()()

()

∞∞

R R K S ac Sln

(2.5)

where c is the concentration of the absorbing species and a is the (base 10) absorp-

tivity, the signal in a DR measurement is given by the difference between the

reﬂ ectance of the reference and the reﬂ ectance of the sample, that is, (1 − R

∞

). For

trace amounts of the analyte, the denominator in the KM function (2 R

∞

) is approxi-

mately equal to 2 and does not vary greatly when the concentration of the analyte

is changed, provided that ac / S is small. As (1 − R

∞

)

is proportional to c, the signal

(1 − R

∞

) is proportional to c

1/2

. The noise across a reﬂ ectance spectrum is approxi-

mately constant. Thus, provided that R

∞

is less than about 0.9, the signal - to - noise

ratio ( S/N ) is proportional to c

1/2

. A reduction in concentration of the absorbing

species by a factor of 100, therefore, only leads to a reduction in S/N by a factor

of 10. The downside of this effect is that small impurities present in the catalyst

(e.g. in the support) can often lead to quite intense bands in the reﬂ ectance

spectrum.

2.3.2

General Remarks on Methodologies for DR UV - V is - NIR Measurements

As indicated in the Introduction, considerations related to the instruments, attach-

ments, cells and experimental setup have been extensively reported, so only a few

fundamental points will be considered here. In the DR UV - Vis experiments, the

light scattered by the solid sample and by the reference is recorded by an integrat-

ing sphere coated with a white standard showing a high diffuse reﬂ ectance, such

as MgO, BaSO

and more recently polytetraﬂ uoroethylene ( PTFE ). Experimental

details of this attachment and cells that can be used for the measurements have

been reported in several articles [4, 9, 13, 31] . By using an appropriate system, in

situ measurements on catalysts treated following speciﬁ c protocols and kept in

controlled atmosphere are possible; and it may be of interest to report that kinetic

aspects of the catalyst activation or of catalyzed reactions can be evaluated (see, for

example, refs. [32, 33] , respectively). Recently, great effort has been applied to

develop operando techniques which refer to the spectroscopy of a working catalyst

in combination with on - line activity measurements [34 – 35] .

2.3.3

UV Absorption Bands of Insulating Oxides: Excitonic Surface States

Insulators such as alumina, silica and alkaline earth oxide s ( AEO ) employed as

catalyst supports or as catalysts have been studied by UV - Vis spectroscopy since

the beginning of the application of optical methods to the investigation of ﬁ nely

divided materials. The basic feature to be considered is that the band gap of

these oxides is so wide that electron transitions from the valence to the conduc-

tion band can be promoted only by electromagnetic radiation in the far/vacuum

UV range ( λ < 192 nm; ν > 52 000 cm

− 1

), requiring special equipment. Neverthe-

less, optical absorptions involving energy states within the main gap produce

optical absorption in the near - UV, and these can be observed using conventional

spectrophotometers (equipped with an integrating sphere, see above). Among

such states are those related the surface, which can be due to the saturation of

surface valence states with

–

OH groups, the presence of supported species (e.g.

TMIs) or coordinative unsaturation (typically appearing after dehydration). As for

surface hydroxyls, their electronic excitation by laser irradiation at 514.5 nm was

found to be responsible for the so called “ ﬂ uorescence ” background of η - Al

and MgO, which strongly affects the ability to measure laser Raman spectra of

species adsorbed on these oxides [36] . Surface states related to the presence of

supported species produce optical absorptions that can be interpreted indepen-

2.3 UV-Vis-NIR Absorption Spectroscopy 61

62 2 The Application of UV-Visible-NIR Spectroscopy to Oxides

dently of the band state model of the support, and these will be considered in

the following sections. Conversely, near - UV - Vis spectroscopy can be considered

a useful tool to obtain speciﬁ c, and in some cases unique, insights on electronic

surface states related to unsaturated sites exposed by insulating oxide - based

materials. UV bands at 240 and 320 nm were observed for a series of zeolites

(faujasite, mordenite, ZSM - 5, erionite, offretite). The ﬁ rst band was related to

framework Al - O units easily removable by dealumination and dehydroxylation,

while the second one was attributed to transitions occurring in an oxoaluminum

structure inside the zeolite matrix [37] . Optical absorption of silica materials has

been thoroughly investigated by physicists [38] , and their results were useful for

the assignment of near - UV bands exhibited by silicas (not structured sol – gel

derived and mesoporous FMS - 16 and MCM - 41) outgassed at T > 673 K to surface

≡

SiO ˙ and

≡

Si ˙ defects sites, produced by dehydroxylation, responsible for the

activity in photometathesis of propene [39] . However, the overwhelming part of

the investigation carried out on the electronic surface states of insulating oxides

has been focused on AEOs, which is still an area of direct interest in base cataly-

sis [40] . In addition, AEOs are regarded as useful model systems for a number

of reasons:

i) Most of them can be obtained in the form of highly dispersed nanocrystalline

powders, with speciﬁ c surface area ranging from ca. 200 to 10 m

− 1

ii) They have a simple crystalline structure (rock salt, based upon interpenetrating

face centered cubic sub - lattices).

iii) {001} cube faces are predominant in the nanocrystals, as evidenced by trans-

mission electron microscopy, allowing even highly rough AEO surfaces to be

described as resulting from the intersection of {001} microfaces [41, 42] .

Nelson and Hale [43] published the ﬁ rst DR spectra of AEO powders. They

showed that highly dispersed systems have UV optical absorption bands that are

not present in the spectra of pure single crystals, which are conversely character-

ized by an extremely low speciﬁ c surface area, and hence an almost negligible

contribution from surface states. Additional evidence was obtained in the follow-

ing years [44, 45] , and a comprehensive analysis of such bands has been reported

by Garrone et al. [46] . The results of this work are an effective example of the wide

set of fundamental information which can be derived from the spectroscopic data

on the nature of optical transitions, structure and reactivity (and their inter - rela-

tionships) of surface sites.

Figure 2.5 summarizes the DR UV spectra of well outgassed samples of MgO,

CaO, SrO and BaO powders considered by those authors. Owing to bulk excitonic

transitions, the edges are clearly visible in the case of SrO and BaO, while for MgO

and CaO they lie beyond the near - UV range (in the dotted part of the spectra). In

the spectrum of each oxide some absorptions at frequencies below that edge are

present, which are assigned to excitonic transitions involving surface sites (and

expected to produce discrete absorptions). Considering SrO ﬁ rst, this latter part

of the spectrum is constituted by two absorptions of comparable intensity (I, II)