Jackson S.D., Hargreaves J.S.J. Metal Oxide Catalysis
Подождите немного. Документ загружается.


Table 3.3 Crystal structures and ion coordinations in solid simple oxides of interest in heterogeneous catalysis.
Cation
valence
Structure
name
Space
group
Z Coordination Examples
Cation Oxide
2 Rock salt Fm 3 m 4 6 (oct) 6 (oct) F
1u
(IR) MgO, CaO, SrO, BaO, MnO, FeO,
CoO, NiO, CdO
Zinc blende
Fm43
4 4 (tetr) 4 (tetr) F
2
(IR,R) BeO (H)
Wurtzite P 6
3
mc 2 4 (tetr) 4 (tetr) A
1
(IR,R) + 2B
1
(in) + E
1
(IR,R) + 2E
2
(R) BeO (L), ZnO
Tenorite C 2/ c 4 4 (sq.pl.) 4 A
g
(R) + 2B
g
(R) + 3A
u
(IR) + 3B
u
(IR) CuO
3 P 3
1
3 3 (trig.) 1, 2 B
2
O
3
Corundum
Rc3
6 6 (oct) 4 2A
1g
(R) + 2A
1u
(in.) + 3A
2g
(in.) + 3A
2u
(IR)
+ 5E
g
(R) + 5E
u
(IR)
α - Al
2
O
3
, α - Cr
2
O
3
, α - Fe
2
O
3
, α - Ga
2
O
3
*
Tetragonal
spinel
I 4
1
/ amd 4 4 (tetr), 6 (oct) 3, 4 2A
1g
(R) + 2B
1g
(R) + 4B
2g
(R) + 6E
g
(R) +
4A
u
(IR) + 6E
u
(IR)
Mn
3
O
4
( δ - Al
2
O
3
)
C 2/ m 4 4 (tetr), 6 (oct) 3, 4 10A
g
(R) + 5B
g
(R) + 8B
u
(R) + 4A
u
(R)
θ - Al
2
O
3
, β - Ga
2
O
3
P 4
1
32 8 4 (tetr), 6 (oct) 3, 4 21F
1
(IR)
γ - Fe
2
O
3
“ A ”
Pm31
1 7 6, 4 2A
1g
(R) + 2E
g
(R) + 2A
2u
(IR) + 2E
u
(IR) La
2
O
3
, Ce
2
O
3
, Pr
2
O
3
(H), Nd
2
O
3
(H)
“ C ” bixbyite
Ia3
6 (oct) 4 4A
g
(R) + 4E
g
(R) + 14F
g
(R) + 5A
u
(in) +
5E
u
(in) + 16F
u
(IR)
Pr
2
O
3
(L), Nd
2
O
3
(L), α - Mn
2
O
3
3.4 The Skeletal IR Spectra of Metal Oxides 113

114 3 The Use of Infrared Spectroscopic Methods
Cation
valence
Structure
name
Space
group
Z Coordination Examples
Cation Oxide
3, 2,3 (Defective)
cubic spinel
Fd 3 m 8 4,6 4 A
1g
(R) + E
g
(R) + F
1g
(in.) + 3F
2g
(R) +
2A
2u
(in) + 2E
u
(in) + 4F
1u
(IR) + 2F
2u
(in)
γ - Al
2
O
3
, η - Al
2
O
3
, γ - Ga
2
O
3
, Fe
3
O
4
, Co
3
O
4
4
α - quartz
P 3
2
21 3 4 (tetr) 2 (bent) 4A
1
(R) + 4A
2
(IR) + 8E(R,IR) SiO
2
, GeO
2
*
Rutile P 4
2
/ mnm 2 6 (oct) 3 A
1g
(R) + A
2g
(in) + B
1g
(R) + B
2g
(R) + E
g
(R)
+ A
2u
(IR) + 2B
1u
(in) + 3E
u
(IR)
TiO
2
, MnO
2
, GeO
2
, SnO
2
, β - PbO
2
Anatase I 41/ amd 4 6 (oct) 3 A
1g
(R) + A
2u
(IR) + 2B
1g
(R) + B
2u
(in) +
3E
g
(R) + 2E
u
(IR)
TiO
2
*
Baddeleyite P 2
1
/ c 4 7 3, 4 9A
g
(R) + 9B
g
(R) + 8A
u
(IR) + 7B
u
(IR) ZrO
2
(L)
Tetragonal
zirconia
P 4
2
/ nmc 2 8 4 A
1g
(R) + 2B
1g
(R) + 3E
g
(R) + A2
u
(IR) +
B2
u
(in) + 2E
u
(IR)
ZrO
2
(M)
Fluorite Fm 3 m 4 8 (cub.) 4 F
1u
(IR) + F
2g
(R) ThO
2
, CeO
2
, HfO
2
, ZrO
2
(H)
5 V
2
O
5
Pmmn 2 5 (6) 1, 2, 3 7A
g
(R) + 7B
1g
(R) + 3B
2g
(R) + 4B
3g
(R) +
3A
u
(in) + 3B
1u
(IR) + 6B
2u
(IR) + 6B
3u
(IR)
V
2
O
5
, R - Nb
2
O
5
*
6 ReO
3
Pm 3 m 4 6 2 2 F
1u
(IR) + F
2u
(in) ReO
3
dist. = distorted; * = metastable phases; L = low temperature form; H = high temperature form; P = high - pressure form.
Table 3.3 Continued
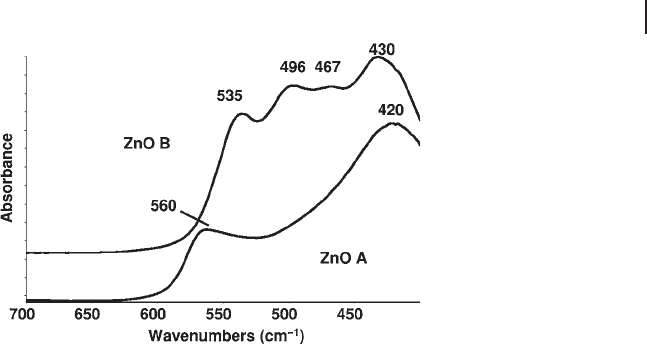
The effect of morphology is even more evident in the IR spectrum of ZnO
(Figure 3.4 ). This solid belongs to the wurtzite - type structure (wurtzite is the hex-
agonal polymorph of ZnS), space group P 6
3
mc with Z = 2. As shown in Table 3.3
the irreducible representation for this structure forecasts two IR active modes (A
1
+ E
1
). The two TO fundamental modes are observed, in ZnO monocrystals, at 380
and 407 cm
− 1
[48] , the corresponding LO modes baing observed at 574 and 583 cm
− 1
.
The resolution of the two vibrational modes is generally not evident in the IR
spectra of ZnO powders. According to Andr é s Verg é s and coworkers [49], thin
lamellar ZnO particles show two peaks at 580 cm
− 1
(weak LO) and 406 cm
− 1
(strong,
TO). One peak only should be observed for spherical particles, at 494 cm
− 1
. In the
spectrum of sample A reported in Figure 3.4 , lower spectrum, the particles are
lamellar and relatively large and thick, while those of sample B are smaller, highly
porous, with two main kinds of morphologies, lamellar (bands at 535 and 438 cm
− 1
)
and ellipsoidal (bands at 496, 467 cm
− 1
).
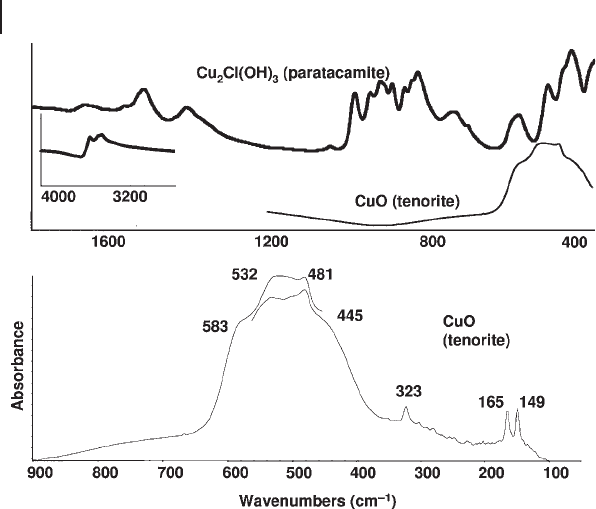
The spectrum of CuO (tenorite) is more complex, characterized by six IR active
modes, with at least three sharp peaks in the FIR spectrum (Figure 3.5 ).
3.4.1.2 Oxides of Trivalent Elements and Spinel - Type Structures
IR spectroscopy can be used to distinguish the different polymorphs of trivalent
metal oxides. γ - Al
2
O
3
, which is the most commonly used form of alumina in
catalysis, is mostly obtained by decomposition of the boehmite oxyhydroxide, γ -
AlOOH, or of a poorly crystallized hydrous oxyhydroxide called “ pseudobohemite ”
at 600 – 800 K. It has a cubic structure and is described as a defective spinel,
although it can be tetragonally distorted. However, its structure is still under
investigation and debate [50, 51] . Calcination at increasing temperatures gives rise
to the transformation sequence γ - Al
2
O
3
→ δ - Al
2
O
3
→ θ - Al
2
O
3
→ α - Al
2
O
3
. δ - Al
2
O
3
is a tetragonal spinel superstructure whose unit cell is constituted by three spinel
unit blocs with tetragonal deformation, probably with a partial ordering of Al ions
Figure 3.4 FTIR skeletal spectra of two different ZnO samples
of ZnO. A: surface area 70 m
2
g
− 1
; crystal size 5 µ m, porous.
B: surface area 4.8 m
2
g
− 1
; particle size 0.2 µ m.
3.4 The Skeletal IR Spectra of Metal Oxides 115
116 3 The Use of Infrared Spectroscopic Methods
into octahedral sites. It is formed continuously in the temperature range 800 –
900 K. θ - Al
2
O
3
is formed above 900 K with simultaneous decrease of the surface
area to near 100 m
2
g
− 1
or less. Its monoclinic structure, which is the same as that
of β - gallia, can be derived from that of a spinel, with deformation and some order-
ing of the defects, with half tetrahedral and half octahedral Al ions. α - Al
2
O
3
(corundum) where all Al ions are equivalent in octahedral coordination in a hex-
agonal close packed oxide array is the thermodynamically stable phase at any
temperature and pressure. Alternatively, η - Al
2
O
3,
also considered to be a spinel
structure, is obtained by decomposing Bayerite Al(OH)
3
. Calcination gives rise to
the sequence η - Al
2
O
3
→ θ - Al
2
O
3
→ α - Al
2
O
3
.
Figure 3.6 shows the evolution of the medium IR spectra of a pseudobohemite
precipitate with calcination, revealing the formation of different phases. The cubic
spinel structure, irrespective of the cation distribution of normal, inverted or
random spinels, as well as of defective spinels, belongs to the OFdm
h
7
3= space
group with Z = 8. Five Raman active modes and four IR active modes occur. The
spectrum of γ - Al
2
O
3
is generally mostly characterized by two very broad bands in
the medium IR region at 580 and 880 cm
− 1
, respectively, possibly mostly due to
vibrations of Al oxide octahedra and tetrahedra, respectively. According to its
tetragonal spinel superstructure, 10 IR active modes are expected in the IR spec-
trum of δ - Al
2
O
3
which in fact shows more components. The spectrum of θ - Al
2
O
3
,
a deformed ordered spinel superstructure, presents several sharp maxima, in
agreement with the forecast of 12 fundamental vibrations. The six fundamental
Figure 3.5 FTIR skeletal spectra of paratacamite (Cu
2
Cl(OH)
3
)
and its decomposition product tenorite (CuO).

TO modes of α - Al
2
O
3
[52] (Figure 3.7 , lower part, where both the medium and the
far IR regions are shown) correspond to the maxima at 636, 581, 439, 405 and
382 cm
− 1
and to the shoulder at 560 cm
− 1
. No fundamental TO modes are observed
above 700 cm
− 1
, in agreement with the six - coordination only for Al in this structure.
The bands at 871 and 490 cm
− 1
are due to LO modes [53] .
Figure 3.6 FTIR skeletal spectra of the evolution products of
calcination of a bohemite ( γ - AlOOH) precipitate.
Figure 3.7 FTIR and FTFIR skeletal spectra of α - Al
2
O
3
(corundum) and of a β - alumina with composition BaAl
9
O
14.5
.
3.4 The Skeletal IR Spectra of Metal Oxides 117
118 3 The Use of Infrared Spectroscopic Methods
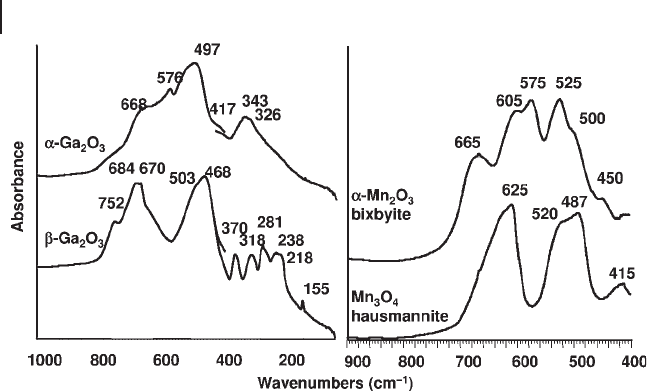
Similarly, is possible to readily distinguish α - Ga
2
O
3
, metastable with only octra-
hedral coordination for Ga ions, from β - Ga
2
O
3
which is the thermodynamically
stable form with both tetrahedral and octahedral coordination for Ga ions (see
Figure 3.8 , left). The strong similarity of the spectra of α - Ga
2
O
3
and α - Al
2
O
3
, both
corundum structures, is also evident (Figure 3.4 , lower left and Figure 3.5 , upper
part).
Skeletal IR spectroscopy is able to distinguish the polymorphs of ferric oxide
( γ - Fe
2
O
3
, maghemite, which is also a spinel - derived structure, has a much more
complex spectrum than the thermodynamically stable polymorph, α - Fe
2
O
3
, hema-
tite) and both are well distinguished from the spinel mixed valency oxide, magne-
tite, Fe
3
O
4
. Similarly, α - Mn
2
O
3
, bixbyite (type C structure) is easily distinguished
from housmannite, the random tetragonal spinel Mn
3
O
4
(Figure 3.8 , right) and
from γ - Mn
2
O
3
, reported to have a distorted spinel structure [54] . Also the so - called
A, B and C rare earth sesquioxides can easily be distinguished by IR spectroscopy
[55] .
3.4.1.3 Oxides of Tetravalent Elements
IR and Raman spectroscopy can also be applied to distinguish the rutile and
anatase TiO
2
polymorphs [56] . Anatase has four IR active skeletal modes while
rutile has only three. The skeletal spectra of both are quite sensitive to particle size
and morphology. The spectrum of anatase powders is mostly associated with two
strong bands at 330 and 480 cm
− 1
, with a broad absorption with some component
at higher frequency. The evolution of anatase (metastable) towards rutile (stable)
is associated with the appearance of a third strong component in the middle (near
420 cm
− 1
) and the shift of the other maximum upwards to 520 cm
− 1
.
IR spectra clearly distinguish the three zirconia polymorphs [57] . The high -
temperature cubic phase has only one IR active skeletal mode, found near 550 cm
− 1
for powders, while tetragonal zirconia (the medium - temperature polymorph) has
Figure 3.8 FTIR skeletal spectra of β - Ga
2
O
3
, α - Ga
2
O
3
, α - Mn
2
O
3
and Mn
3
O
4
.

three IR active modes, and presents a broad multiple maximum near 500 cm
− 1
,
with weaker components near 575 and 160 cm
− 1
. Monoclinic zirconia (baddeleyite)
has a much more complex spectrum, with 15 IR active modes. In particular it is
well characterized by a strong band evident at 770 cm
− 1
, associated with the move-
ment of oxygen in threefold coordination.
IR spectroscopy allows the analysis of the many polymorphs of manganese
dioxide [54] such as α - MnO
2
(hollandite, tetragonal, SG I 4/ m ), R - MnO
2
(ramsdel-
lite, orthorhombic, Pbnm ), β - MnO
2
(pyrolusite, tetragonal rutile structure, P 4
2
/
mnm ), γ - MnO
2
(nsutite, hexagonal), δ - MnO
2
(vernadite, hexagonal) and λ - MnO
2
(spinel - type, cubic, Fd 3 m ).
α - and β - quartz, α - and β - cristobalite, tridymites, coesite, morganite and sili-
calite are different polymorphs of silica with tetrahedrally coordinated silicon. So,
their vibrational structure, as well as that of amorphous or vitreous silica, in which
Si is also tetrahedral, can be discussed in parallel. The IR spectra of all tetrahedral
silica polymorphs have bands in three regions: in the region 1300 – 950 cm
− 1
(very
strong, denoted ν
1
), 850 – 600 cm
− 1
(medium strength, ν
2
) and near 450 cm
− 1
(very
strong, ν
3
). Raman spectra show very weak peaks in the 1300 – 950 cm
− 1
and 850 –
700 cm
− 1
regions ( ν
1
and ν
2
modes), and one or more very strong peaks below
550 cm
− 1
, in a position very sensitive to the overall crystal structure of the solid
( ν
4
). These features are also present in the spectra of amorphous or vitreous silica;
so they represent vibrations of the basic structural units of both crystalline and
amorphous silica, that is, SiO
4
tetrahedra and bridging oxygens.
Four main vibrational modes are expected for a tetrahedral silica network. In
the C
2v
symmetry of the Si
–
O
–
Si bent units, a symmetric stretching (A
1
), an asym-
metric stretching (B
1
), a bending (A
1
) and a rocking mode (B
2
) are expected, the
modes with A
1
, B
1
and B
2
symmetry being both IR and Raman active. The stron-
gest Raman mode, ν
4
, is assumed to be a symmetric stretching mode, mainly
because Raman peak intensity is generally greater for stretching than for bending
modes. However, the coupling of this mode with the Si
–
O
–
Si scissoring mode
provides an explanation of the low frequency of the strongest Raman peak (550 –
350 cm
− 1
) in all silica polymorphs. On the other hand, it is clear that in the solid
state in order for all Si
–
O bonds to expand in - phase, most Si
–
O
–
Si angles must
contract simultaneously. This mode is consequently highly sensitive to the struc-
ture of the polymorph, as is indeed observed. The position of the ν
4
peak, in fact,
strongly depends on the type of ring present in silicas and silicates. As for the IR
spectrum, the strongest complex band is ν
1
, observed in the 1300 – 950 cm
− 1
region
and is associated to the asymmetric stretching of the Si
–
O
–
Si bridges. However,
this mode is split into two components even in the case of vitreous silica, due to
either the in - phase
′
()
ν
1
or the out - of - phase coupling
′′
()
ν
1
of the asymmetric
stretching modes of nearest Si
–
O
–
Si groups. In other words, this mode couples
with the symmetric and asymmetric stretching of the four Si
–
O bonds of the SiO
4
octahedra. The position of both
′
ν
1
and
′′
ν
1
components is also somewhat sensitive
to the size of the rings and/or to the density of the different silica polymorphs.
This is particularly true for
′
ν
1
, whose shift is stronger, so that it is actually resolved
from
′′
ν
1
only in some cases. As discussed above, the ν
2
mode is essentially a
3.4 The Skeletal IR Spectra of Metal Oxides 119
120 3 The Use of Infrared Spectroscopic Methods
bending mode of the Si
–
O
–
Si bridges, although mixed with a symmetric stretch-
ing mode. Its assignment predominantly to a bending mode is made mainly due
to its weakness in the Raman spectra, although its position is more typical of a
symmetric stretching mode. This mode appears to be the least sensitive to the
structure, although in some cases it splits defi nitely into more components, as in
the case of α - quartz where three well - resolved sharp bands are found. The lowest
frequency IR mode, ν
3
, is associated with the out - of - plane deformation of the Si
–
O
–
Si bridges, that is, a “ rocking ” mode. This explains why this mode is essentially
silent in the Raman spectrum, while being very strong in IR in the region 430 –
490 cm
− 1
in all silica forms. Besides the four vibrational modes discussed here that
are common to all silicas, network silicates and silico - aluminates, other structure -
sensitive features are frequently present. They are associated with the splitting of
these vibrational modes (bands above 350 cm
− 1
) or to torsional lattice modes (below
400 cm
− 1
).
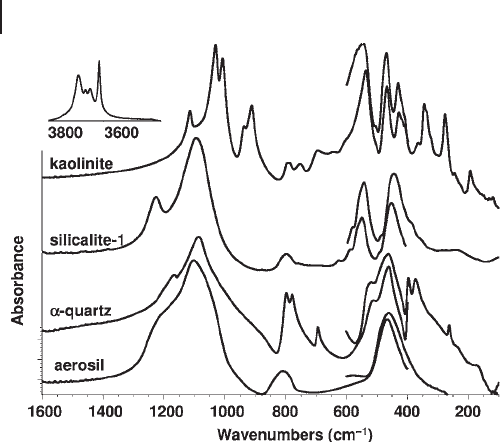
In Figure 3.9 the FTIR - FTFIR transmission - absorption spectra of an amorphous
silica sample (aerosil) and of two crystalline powders ( α - quartz and silicalite - 1) are
compared. The ν
1
, ν
2
and ν
3
absorptions (broad) discussed above are evident for
amorphous silica. In the case of quartz, sharper components are observable as
expected. Ten maxima can be easily observed at 1165, 1086, 798, 779, 694, 519,
463, 397, 373 and 263 cm
− 1
. The irreducible representation for α - quartz (taking the
right - handed enantiomorph with space group PDZ321 3
23
6
==,with ) is 4 A1 (R)
+ 4 A2 (IR) + 8 E (R,IR) so that 12 IR active fundamental modes are expected, each
one undergoing TO - LO splittting. Actually, in the ν
1
region (asymmetric Si
–
O
–
Si
stretching) we expect three fundamental modes, so that in the maximum at
1086 cm
− 1
, which shows shoulders at both sides, certainly more components are
Figure 3.9 FTIR and FTFIR skeletal spectra of amorphous
silica (aerosil), α - quartz, silicalite - 1 and kaolinite.

superimposed. Three resolved components are found as expected in the ν
2
region.
One fundamental mode is expected to be very weak near 130 cm
− 1
, and this could
not be detected.
Silicalite - 1 is the totally siliceous form of the zeolite MFI (ZSM - 5), another silica
polymorph. It belongs to the
PnC
h
2
12
5
= monoclinic space group (n. 14) with Z
= 96. It transforms into an orthorhombic structure, belonging to the
Pnma D
h
=
2
16
space group (n. 62) between 350 and 363 K. Substituted silicalites such as ZSM - 5
zeolite (see below) and Ti - silicalite adopt the orthorhombic structure even at
room temperature, the transition temperature being strongly shifted to lower
temperatures.
Factor group analysis [58] indicates that 429 IR active modes and 432 Raman
active modes are expected for the monoclinic structure and 323 IR active modes
and 432 Raman active modes are expected for the orthorhombic form. Only 16
components in the IR specrum and 11 components in the Raman spectrum are
observed because of the superimposition of many of the expected fundamentals.
However, a careful observation of the spectra, with the help of analysis of the per-
turbations arising from isomorphic substitution and with the aid of derivative
spectra, showed the presence of a great number of very weak components (shoul-
ders) in the spectra.
3.4.2
Crystalline Complex or “ Mixed ” Oxides
3.4.2.1 Solid Solutions
Vibrational spectroscopies give rise to interesting information on the microscopic
structure of solid - solution mixed oxides. For example, the state of vanadium in
solid solution in TiO
2
anatase catalysts [59] , the partial ordering of cations in
corundum - type Fe - Cr oxides [60] , the real presence of Ti
4+
in the silicalite frame-
work of TS1 catalysts [58] and the solubility of Al
3+
ions in the NiO rock - salt
structure [61] have been objects of IR spectroscopic studies.
3.4.2.2 Ternary Phases
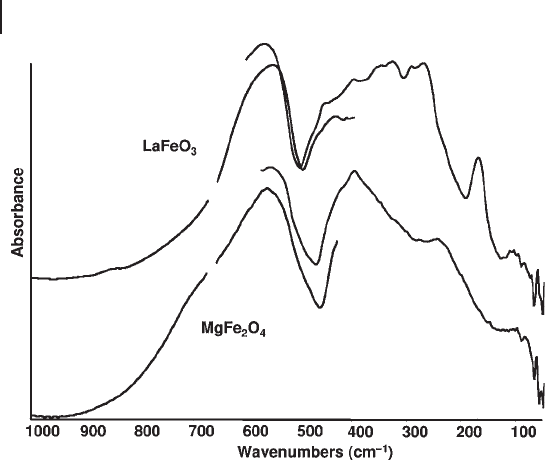
IR spectroscopy has been largely used to characterize normal, inverse, random
and non - stoichiometric AB
2
O
4
spinel - type structures , such as many divalent alumi-
nates, gallates, ferrites and chromites [62] , including superstructures such as those
of the defective spinel sesquioxides γ - Fe
2
O
3
, θ - Al
2
O
3
and β - Ga
2
O
3
. In Figure 3.10
the spectrum of the predominantly inverse spinel MgFe
2
O
4
is reported, showing
three of the four IR active fundamental modes at 563, 402 and 250 cm
− 1
, the fourth
one being expected to be at very low frequency.
The so - called beta - aluminas are characterized by the existence of layered blocks
of a trivalent element (most frequently Al
3+
, but also Fe
3+
and Ge
3+
) with the same
spinel structure separated by “ mirror planes ” where large monovalent (Na or K),
divalent (Ba, and sometimes Ca or Sr) and trivalent (La) cations, which do not
enter the cubic close packed array of oxide ions of the spinel blocks, are located,
together with oxide anions bridging between the blocks. In these planes the cations
3.4 The Skeletal IR Spectra of Metal Oxides 121
122 3 The Use of Infrared Spectroscopic Methods
are able to diffuse. The metal - to - oxygen stretches involving such ions located in
the mirror planes occur in the low - frequency region (FIR). In Figure 3.7 , top, the
spectrum of a solid with composition BaAl
9
O
14.5
, belonging to the beta - alumina
family, is reported. At least 34 components may be distinguished, in good agree-
ment with what is expected based on the factor group analysis [63] . The low -
frequency bands due to vibrational modes directly involving Ba ions are marked
with asterisks in Figure 3.7 : those at 73 and 67 cm
− 1
are attributed to Ba ions in
the interlayer region, while the peak at 111 cm
− 1
is attributed to interstitial Ba in
the spinel blocks in this Ba - rich phase.
IR spectroscopy can be used to distinguish several different phases characterized
by the stoichiometry ABO
3
(Table 3.4 ), such as cubic, tetragonal, orthorombic and
rhom bohedral perovskites (such as SrTiO
3
, BaTiO
3
, LaFeO
3
and LaMnO
3
, respec-
tively [56, 64, 65] ), from ilmenites and lithium niobate structures. In Figure 3.10
the spectrum of LaFeO
3
is reported. It shows some of the 26 IR active modes
expected.
3.4.2.3 Oxo - Salts
Oxo - salts involve oxo - anions, which are internally held by covalent bonds between
the non - metal atom (or the metal in a very high oxidation state) and oxygen, giving
rise to M
–
O bond orders ranging between 1 and 2. The oxo - anions are further
bonded through ionic interactions with the metal cations. So, the vibrational
spectra of oxo - salts are dominated, in their high - frequency ranges, by the “ inter-
nal ” vibrations of the oxo - anion. Obviously, splittings of these internal vibrations
occur in principle as a result of the couplings of the modes of more than one oxo -
anionic units simultaneously present in the smallest Bravais cell.
Figure 3.10 FTIR and FTFIR skeletal spectra of LaFeO
4
and MgFe
2
O
4
.
