Ивантер Э.В., Коросов А.В. Введение в количественную биологию

Подождите немного. Документ загружается.

Задача «Доказать отличие нескольких выборок»

130

тролируемого фактора (x

факт.

) и действия случайных причин (x

случ.

= M ±x

факт.

±x

случ.

Иными словами, отклонение варианты от общей средней свя-

зано с отклонением за счет действия изучаемого фактора и за счет

действия прочих неучтенных факторов.

Каждой дозе изучаемого фактора соответствует одна выборка

(градация). Поэтому каждая групповая (выборочная) средняя будет

характеризовать реакцию объектов на соответствующую дозу изу-

чаемого фактора и эффект изучаемого фактора можно выразить как

отклонение групповой средней от общей средней:

факт.

= M

–

В свою очередь, от групповой средней каждая варианта будет

отличаться в силу случайных неучтенных причин, эффект действия

случайных факторов можно выразить как отклонение отдельной ва-

рианты от данной групповой средней:

случ.

= x

– M

Получается, что отклонение варианты от общей средней бу-

дет равно отклонению групповой средней от общей средней (эффект

учтенного фактора) и отклонению варианты от своей групповой

средней (эффект неучтенных факторов). Отсюда

–

M) = (M

– M) + ( x

– M

Обобщая эту запись для всех вариант выборки (возведя в

квадрат и суммировав), получаем правило разложения общей вариа-

ции признака на составные части, отражающие влияние всех на-

званных причин:

общ

= С

факт

+ С

случ

Общая сумма квадратов признака рассчитывается как сумма

квадратов отклонений всех вариант (x

) от общей средней (M):

общ

= Σ (x

– M)².

Факториальная сумма квадратов рассчитывается как сумма

квадратов отклонений частных средних (M

) для каждой выборки

(всего k выборок) от общей средней:

факт

= Σ (M

– M)².

Остаточная (случайная) сумма квадратов есть сумма квадра-

тов отклонений вариант каждой выборки (x

) от своей средней (M

случ

= Σ (x

– M

)².

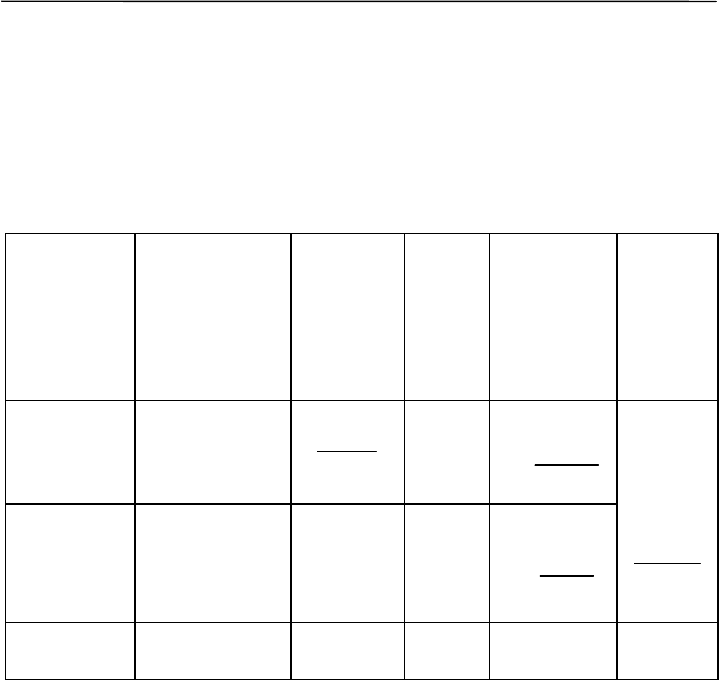
Параметры дисперсионного анализа и порядок их вычисле-

ний представлены в таблице 7.2.

Задача «Доказать отличие нескольких выборок»

131

Отношение сумм квадратов (SS, sum of squares) к соответст-

вующему числу степеней свободы дает оценку величины дисперсии,

или средний квадрат (MS, mean square), иногда ее именуют вариан-

са. Влияние изучаемого фактора отражает факториальная, или меж-

групповая, дисперсия S²

факт

, а влияние случайных неорганизован-

ных в данном исследовании причин – случайная, или внутригруппо-

вая, остаточная дисперсия S²

случ

, или S²

остат

Таблица 7.2

Состав-

ляющие

диспер-

сии

Суммы

квадратов

(SS),

Сила

влия-

ния,

η²

Сте-

пени

сво-

боды,

Диспер-

сии

(средний

квадрат,

MS),

S²

Кри-

терий

влия-

ния,

Фактори-

альная

факт

Σ (M

– M)²

общ

факт

k–1

S²

факт

F =

Случай-

ная

случ

Σ (x

– M

)²

n–k

S²

случ

факт

Общая

дисперсия

общ

Σ (x

– M)²

Сила влияния фактора определяется как доля частной суммы

квадратов в общем варьировании признака. Показатель силы влия-

ния изучаемого фактора составляет: η²

факт.

= С

факт

./ С

общ

неоргани-

зованных (случайных): η²

случ

= С

случ

/ С

общ

;

сумма этих показателей,

естественно, равна единице: η²

факт

.+ η²

случ

. = 1.

В то же время нам кажется, что придавать большое значение

этому индексу не стоит. Во-первых, в литературе показано, что он

дает не точную характеристику вклада фактора в общую изменчи-

вость и для него приходится рассчитывать некую поправку. Во-вто-

рых, утверждение вроде «фактор влияет с силой 20%» ничего не

передает, кроме впечатления о не очень большом влиянии фактора.

Гораздо интереснее было бы дать прогноз возможных значений

результативного признака при том или ином уровне действия фак-

Задача «Доказать отличие нескольких выборок»

132

тора, а это можно сделать только с помощью регрессионного анали-

за или имитационного моделирования. По этим причинам мы реко-

мендуем рассматривать показатель η

факт.

как простую и удобную

характеристику влияния фактора на признак, подталкивающую ис-

следователя к решению о необходимости продолжения биометриче-

ского исследования в рамках регрессионного анализа. Чем большую

долю в общей дисперсии занимает ее факториальная часть, тем

большая часть общего разнообразия обусловлена варьированием за

счет действия фактора.

Нулевая гипотеза гласит: «влияние фактора на признак от-

сутствует». Проверяют гипотезу по критерию Фишера:

F = S²

факт

/ S²

случ

≥

),,(

dfdfa

F ,

где df

= k–1, df

= n–k,

k – число градаций результативного признака,

n – общий объем всех выборок по всем градациям.

Влияние считается достоверным, если величина расчетного

критерия равна или превышает свое табличное значение с принятым

уровнем значимости (обычно α = 0.05) (F определяется по табл. 7П).

Дисперсионный анализ для количественных признаков

Однофакторным называется анализ, изучающий действие на

результативный признак только одного организованного фактора А.

Для примера оценим влияния растворенного в воде вещества на

плодовитость дафний, используемых в качестве тест-объектов в

водно-токсикологических экспериментах. В ходе предварительного

исследования были получены четыре выборки, четыре группы зна-

чений плодовитости животных, выращенных в средах с разным со-

держанием химической добавки.

Сначала необходимо сгруппировать выборочный материал в

комбинативную таблицу (организовать дисперсионный комплекс).

Для этого варианты каждой выборки записываются в отдельные

графы, именуемые градациями (табл. 7.3). Результативным призна-

ком служит средняя плодовитость дафний за неделю (для иллюстра-

тивности расчетов она дана в целых числах). В нашем примере ор-

ганизованы 4 градации – чистая вода (контроль, градация А1; значе-

ния плодовитости 6, 5, 5, 7), слабая концентрация вещества (5 мг/л,

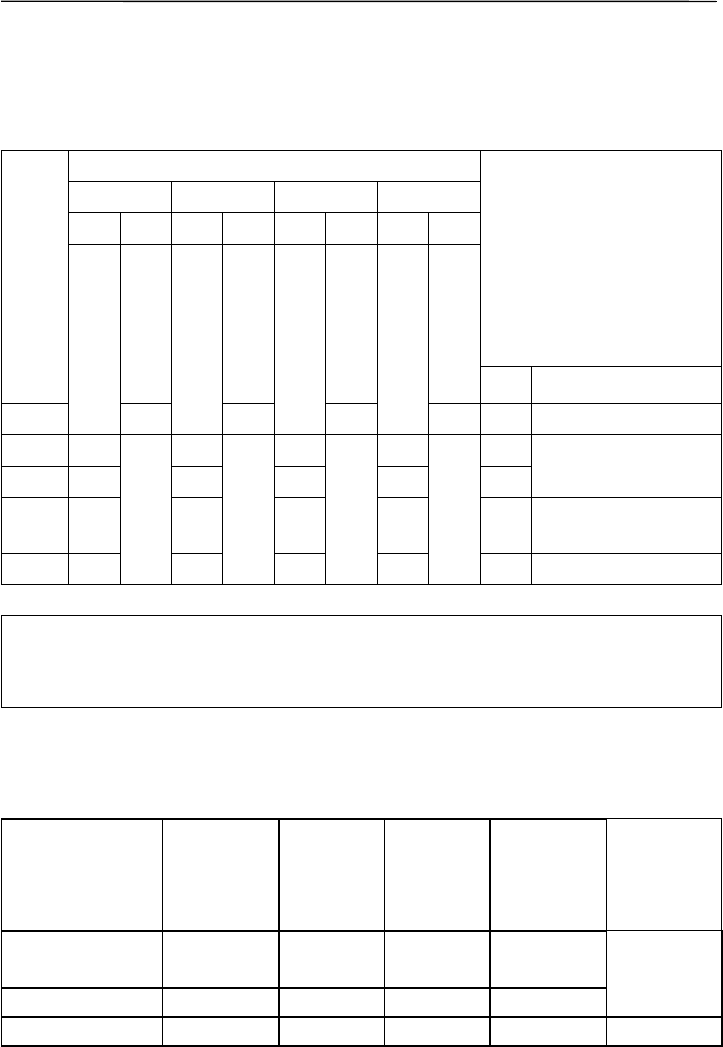
Задача «Доказать отличие нескольких выборок»

133

А2; 8, 7, 6, 6), средняя (15 мг/л, А3; 8, 8, 7) и сильная (30 мг/л, А4;

8, 7, 9). Предлагаемый ниже алгоритм расчетов позволяет использо-

вать неравное число вариант в градациях. Расчеты несложны и по-

казаны в таблице 7.3.

Таблица 7.3

Градации фактора

x x

6 36 8 64 8 64 8 64

5 25 7 49 8 64 7 49

5 25 6 36 7 49 9 81

7 49 6 36

Σx² 135

185

177

194

691

H1 = ΣΣx² = 691

Σx 23 27 23 24 97 H2 = (ΣΣx)²/n =

n 4 4 3 3 14 = (97)²/14 = 672

Σx²/n

132

182

176.3

192

682.8

H3 = ΣΣx²/n =

= 682.8

M 5.8

6.8

7.67

8 6.93

факт

= H3 – H2 = 682.8 – 672 = 10.76

случ.

= H1 – H2 = 691 – 672 = 8.17

общ.

= H1 – H3 = 691 – 682.8 = 18.93

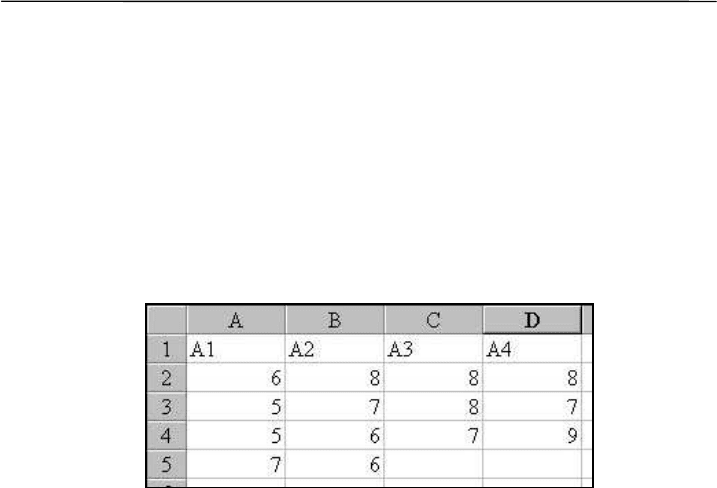
Полученные значения позволяют вычислить дисперсии, оп-

ределить силу влияния фактора и критерий достоверности Фишера.

Состав-

ляющие

дисперсии

Суммы

квадра-

тов,

Сила

влия-

ния,

Степе-

ни сво-

боды,

Диспер-

сии, S²

Крите-

рий,

Факториаль-

ная

10.76 57% 3 3.59

Случайная 8.17 10 0.82 4.39

Общая 18.93 4.39

Задача «Доказать отличие нескольких выборок»

134

Поскольку полученное значение критерия (F = 4.39) больше

табличного (F

(0.05,3,10)

= 3.7) (табл. 7П), отличие факториальной и

случайной дисперсий достоверно, влияние фактора значимо.

Отсюда следует биологический вывод: стимулирующее

влияние изучаемого фактора (вещества) на плодовитость дафний от-

носительно велико (57%) и достоверно (с вероятностью Р>0.95).

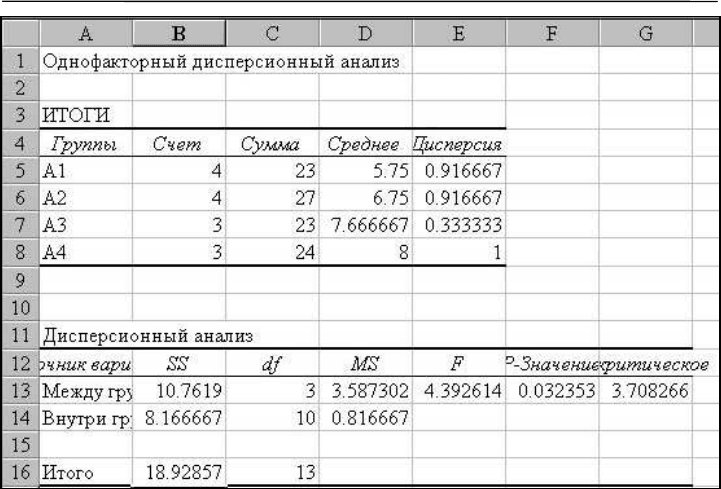
Выполнить дисперсионный анализ по представленному алго-

ритму можно и в среде Excel. Для этого введем подписанные метка-

ми (А1, А2…) данные в четыре столбца, отдельно для каждой града-

ции.

Вызовем программу обработки командой Сервис \ Анализ

данных…\ Однофакторный дисперсионный анализ, ОК. Заполним

окно макроса, выделив блок данных с метками и поставив галочку в

поле «Метки в первой строке», ОК. На новом листе (рис. 7.1) поя-

вятся результаты расчетов, идентичные приведенным в табл. 7.3.

Чтобы все надписи были видны, нужно изменить ширину столбцов.

Это можно сделать, нажав на серый квадрат слева вверху листа (над

1, левее А), перевести курсор на границу между любыми столбцами

(курсор примет форму креста со стрелками, направленными в сто-

роны) и дважды кликнуть левой кнопкой мыши. Ширина каждого

столбца будет автоматически определена по максимально длинному

содержимому какой-либо ячейки этого столбца.

С помощью макроса Однофакторный дисперсионный анализ

в рамках пакета Excel можно обрабатывать выборки самого разного

размера, в том числе очень большого, поэтому мы не приводим спе-

циальных алгоритмов для ручного обсчета больших выборок.

Задача «Доказать отличие нескольких выборок»

135

Рис. 7.1. Дисперсионный анализ в среде Excel

Парные сравнения выборочных средних методом Шеффе

Дисперсионный анализ позволяет установить достоверность

отличия нескольких средних арифметических друг от друга, но он

не сообщает, какие именно средние от каких именно средних отли-

чаются. Может статься, например, что действие фактора вызывает

более или менее плавное изменение средних без заметных перело-

мов в этой тенденции. При этом биологический вопрос может со-

стоять в том, чтобы определить минимальную дозу фактора, которая

по сравнению с контролем значимо влияет, изменяет среднюю для

этой градации, т. е. определить «первую действующую концентра-

цию». Казалось бы, этот вопрос относится к задаче сравнения двух

выборок: контрольная выборка поочередно сравнивается с выбор-

ками, полученными для все возрастающих доз фактора, а первое

достоверное отличие средних как раз и означает, что данная доза

уже «действующая». Однако с точки зрения статистики такое срав-

нение оказывается некорректным и неточным.

Задача «Доказать отличие нескольких выборок»

136

При таком «лобовом» попарном сравнении выборок одна из

них (для градации контроля) все время участвует в этой процедуре,

на основании которой формулируются разные статистические выво-

ды о достоверности отличий средних с той или иной вероятностью.

Тем самым эти выводы оказываются зависимыми друг от друга. До-

верительная вероятность каждого из этих выводов поэтому от срав-

нения к сравнению уменьшается! Чем больше выводов сделано на

одном и том же материале, тем меньше вероятность их справедли-

вости.

Второе негативное обстоятельство связано с тем, что такая

процедура учитывает далеко не всю информацию о явлении. Дейст-

вительно, изменчивость вариант комплекса выборок (в нашем при-

мере было 14 вариант в 4 выборках) определяется как действием

изучаемого фактора, так и множеством других не учитываемых,

случайных, причин. При сравнении же всего двух выборок (напри-

мер, выборок 1 и 4) эта случайная изменчивость представлена не

всем объемом информации, но только той частью, что проявилась в

рамках этих двух сравниваемых выборок (две выборки содержат

лишь 7 вариант). Поэтому оценки случайной изменчивости для двух

выборок оказываются не столь точными, как могли бы быть по всем

градациям.

Улучшить ситуацию позволяет метод попарного сравнения

выборок, проводимый на базе однофакторного дисперсионного ана-

лиза (метод Шеффе). Для сравнения двух средних предлагается кри-

терий F Фишера, в числителе которого стоит оценка действия фак-

тора (разность средних) для любых двух сравниваемых градаций, а в

знаменателе – оценка случайной изменчивости, общая для всего

дисперсионного комплекса:

),,(

)1(

)(

dfdf

случ.













+⋅⋅−

−

= ,

где M – средние арифметические для любых двух (i, j) градаций

однофакторного дисперсионного комплекса,

S²

случ

– оценка случайной изменчивости из таблицы диспер-

сионного анализа,

k – число градаций фактора,

Задача «Доказать отличие нескольких выборок»

137

, n

– объемы выборок сравниваемых градаций,

α – принятый уровень значимости (обычно α = 0.05),

df – число степеней свободы df

= k–1, df

= (k–1)·(n–1).

Отличия средних считаются достоверными, если расчетное

значение критерия Фишера превысит табличное F

(

,df1,df2)

(табл. 7П).

Сопоставляя выборочные средние для первой и четвертой

градаций нашего примера (табл. 7.3), имеем:

1,4

= (5.8–8)²/[(4–1)· 0.82·(1/4+1/3)] = 3.37,

= 4–1 = 3; df

= (4–1)·(14–1) = 39,

(0.05,3,39)

= 2.87.

Полученное значение (3.37) больше табличного (2.87), следо-

вательно, между средними арифметическими первой и последней

градаций есть достоверное отличие; разные дозы фактора действи-

тельно вызывают изменение плодовитости дафний.

Сравнение выборок первой и второй градаций показывает,

что низкие дозы фактора в них не позволяют говорить о существен-

ном влиянии на дафний: для данных объемов выборок полученное

значение критерия (0.69) меньше табличного (2.87).

F = (5.8–6.8)²/[(4–1)· 0.82·(1/4+1/3)] = 0.69 < 2.87.

Непараметрический однофакторный дисперсионный анализ

Рассмотренные выше схемы дисперсионного анализа исхо-

дили из предположения о нормальном распределении изучаемого

результативного признака. Когда для какого-либо признака нет уве-

ренности, что выполняется предположение о нормальном распреде-

лении изучаемого признака, когда требуется провести анализ быст-

ро и без особой точности, когда мало данных или они выражены ка-

чественными признаками, можно использовать схему непараметри-

ческого дисперсионного анализа. Этот метод более неприхотлив, но

менее точен, нежели параметрический анализ. Он исследует распре-

деления вариант в нескольких выборках. Нулевая гипотеза состоит в

том, что распределения одинаковы, т. е. выборки взяты из одной ге-

неральной совокупности.

Порядок вычислений состоит в том, что все варианты ранжи-

руются в порядке возрастания. Затем суммируются ранги вариант по

каждой выборке отдельно и рассчитывается критерий:

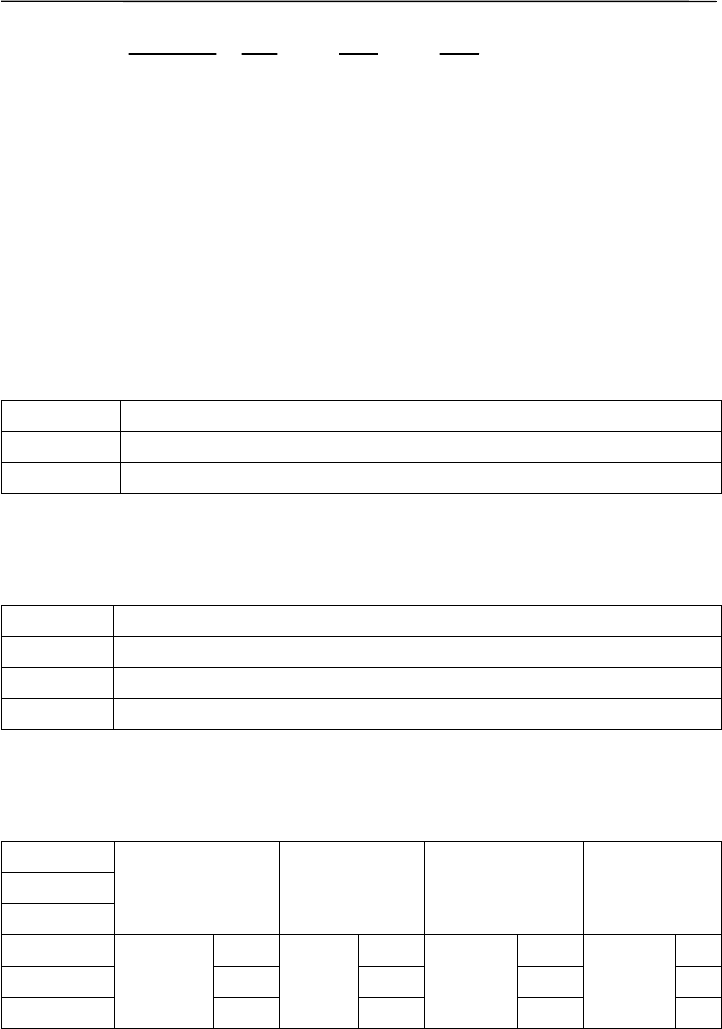
Задача «Доказать отличие нескольких выборок»

138

)1(3......

)1(

+⋅−













++++⋅

−⋅

= n

~ χ²

(

, k–1)

где n – число всех вариант,

– объем j-й градации фактора,

– сумма рангов для каждой j-й градации фактора,

k – число градаций фактора (j

= 1, 2, … k).

При объеме выборок больше 5 вариант статистика H имеет

распределение хи-квадрат с df = k–1 степенями свободы и сравнива-

ется со значениями из табл. 9П.

Применим эту схему (табл. 7.4) к нашим данным из табл. 7.3,

расположив их в строку.

№ п/п 1 2 3 4 5 6 7 8 9 10

Градация

1 1 1 1 2 2 2 2 3 3 3 4 4 4

Значение 5 5 6 7 6 6 7 8 7 8 8 7 8 9

Затем упорядочим и ранжируем. Для нескольких одинаковых

значений берется средний ранг.

№ п/п 1 2 3 4 5 6 7 8 9 10

Градация

1 1 1 2 2 1 2 3 4 2 3 3 4 4

Значение

5 5 6 6 6 7 7 7 7 8 8 8 8 9

Ранг 1.5

1.5

4 4 4 7.5

7.5

11.5

Наконец, разнесем ранги по градациям и подсчитаем необхо-

димые суммы.

Таблица 7.4

Градация

1 1 1

1 2

2 2 3 3 3 4 4 4

Значение

5 5 6

7 6

7 8 7 8 8 7 8 9

Ранг, R 1.5

1.5

7.5 4

7.5

11.5

7.5

11.5

7.5

11.5

Сумма, R

14.5

27 30.5

4 3 3

R²/n

52.56

182.3

310.1

363

Задача «Доказать отличие нескольких выборок»

139

Объем всей выборки равен: n = 14. Величина критерия H составит:

( )

=⋅−+++⋅

⋅

= 1333631.3103.18256.52

14.8645907.89580.065934

−

⋅

По таблице хи-квадрат для α = 0.05 и df = 4–1 = 3 находим:

χ²

(0.05,3)

= 7.81. Полученное значение критерия (14.86) больше таб-

личного (7.81), значит, отличие выборочных распределений досто-

верно. Химическая добавка действительно изменяет плодовитость

дафний.

Сравнение нескольких выборок по изменчивости признака

Одна из задач сравнения двух выборок состояла в том, чтобы

оценить однородность варьирования значений в их пределах, т. е.

чтобы сопоставить множества случайных причин, действовавших

при формировании выборок. Для двух выборок задача решалась с

помощью метода сравнения двух дисперсий по критерию Фишера.

В случае нескольких выборок используется критерий Бартлетта.

С его помощью проверяется нулевая гипотеза о равенстве несколь-

ких дисперсий по всем градациям дисперсионного комплекса (Но:

² = ... = S

= … = S

²) – «фактор, действующий на разные выборки,

не вызывает изменения характера варьирования».

Существенным ограничением для использования этого кри-

терия является требование соответствия сравниваемых распределе-

ний нормальному закону. В другом случае критерий будет фиксиро-

вать не отличие дисперсий, но отличие типов распределений. Это

значит, что уверенность в «нормальности» распределения должна

быть условием выполнения процедуры, рассмотренной ниже.

Метод основан на том известном явлении, что выборочные

дисперсии несколько отличаются от генеральной (в силу ошибки

репрезентативности), а с ростом объема выборки ошибка репрезен-

тативности уменьшается. Это значит, что для принятой нулевой ги-

потезы каждая из выборочных дисперсий (S

²) может отличаться от

общей дисперсии (S²), рассчитанной по всей совокупности, только

случайно. Показано, что сумма отличий выборочных дисперсий от

общей есть случайная величина примерно с χ²-распределением: