Иванов Ю.И., Югай В.Я. Технические средства автоматизации и управления: Методическое руководство к лабораторным работам
Подождите немного. Документ загружается.

1
1
1
1
Программное управление полярностью внутреннего источ-
ника опорного напряжения производится сигналом PB4 микро-
контроллера (логический 0 соответствует положительной по-
лярности). Потенциометр, ручка управления которого находится
на задней панели стенда, позволяет регулировать напряжение на
входе микроконтроллера PA0 от нуля до опорного напряжения
АЦП.
Кнопки управления передней панели формируют сигналы
внешних прерываний INT0 (PD2), INT1 (PD3) и сигналы на
линиях ввода-вывода PB2, PB3 микроконтроллера (табл. 2).
Пассивный уровень сигнала – 1, при нажатии какой-либо кноп-
ки низкий уровень сигнала обязательно поступает на один из
входов прерываний. Кнопки необходимы для передачи команд,
которые управляют выполнением рабочей программы микро-
контроллера, изменяя какие-либо параметры, режимы, реали-
зуемые функции и т.п.
Таблица 2
Кнопка
INT0
(PD2)
INT1
(PD3)
PB2 PB3
>
0 1 1 1
< 1 0 1 1
→ 0 1 0 1
← 1 0 1 0
Таким образом, выполнение стандартных функций, необхо-
димых для реализации типовых задач управления, обеспечива-
ется и микроконтроллером, и дополнительными интерфейсными
устройствами лабораторного стенда.
Подготовка программы микроконтроллера на ассемблере
для процедуры внутрисистемного программирования может
выполняться инструментальным пакетом AVR Studio. Пользо-
вательский интерфейс пакета AVR Studio – стандартный для
Window's–приложений (рис. 2) и содержит полоску меню, па-
1
1
2
2
нель инструментов и рабочую область. Для активизации функ-
ций AVR Studio, необходимых для работы с текстом программы,
должны быть выполнены следующие операции:
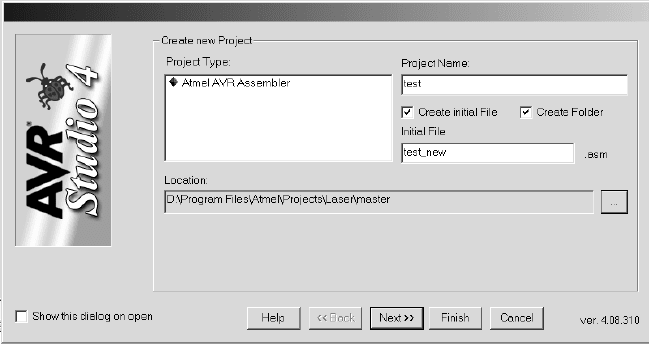
1. Для работы с текстом программы необходимо создать проект
(project). Проект создается с помощью меню Project (пункт
New Project). В появившемся на рабочем поле окне указать
тип проекта – AVR Assembler, имя и путь папки, имя проек-
та. Если проект уже существует, можно открыть его для ра-
боты тем же меню Project (или меню File). Окно с открытым
для работы проектом появится в рабочем поле (рис. 3).
Кнопкой "Next" необходимо определить опции проекта: De-
bug Platform – AVR Simulator, тип микроконтроллера Device
– AT90S8535.
2. Если в открытом проекте уже есть файлы программ на ас-
семблере (с расширением .asm), они будут отображены в ок-
не "Workspace" и их можно открыть в рабочем поле двойным
щелчком левой кнопки мыши. Создать новые файлы (Create
new file) или добавить к проекту созданные ранее файлы
(Add existing file) можно с помощью контекстного меню (или
меню Project), доступ к контекстному меню открывается
щелчком правой кнопки мыши в окне Workspace (рис. 2).
Каждый файл на рабочем поле отображается отдельным ок-
ном. Работа с окнами, подготовка и редактирование текстов
выполняются стандартными средствами Window's–
приложений.
3. Компилятор ассемблера может работать только с одним
файлом, поэтому необходимо указать для компилятора ис-
ходный файл в контекстном меню (Set as Entry File). После
этого можно выполнить запуск компилятора из меню
Project – пункт Build (F7) или соответствующей кнопкой
панели инструментов. По завершении ассемблирования ком-
пилятор сформирует в окне "Output" (рис. 2) сообщение о ре-
зультатах. Если синтаксических ошибок нет, выходной файл
сформирован. Обнаруженные ошибки будут указаны

1
1
3
3
Рис. 2. Интерфейс AVR Studio
1
1
4
4
компилятором (окно "Output"), в сообщении указываются тип
ошибки и номер строки в исходной программе.
Рис. 3. Окно "Create new Project"
Предварительная проверка подготовленной программы
после устранения синтаксических ошибок производится с
помощью симулятора (Debug Platform – AVR Simulator). Запуск
симулятора производится из меню Project – пункт Build and
Run (Ctrl+F7) или соответствующей кнопкой панели инстру-
ментов. Включение различных функций симулятора, режимы их
моделирования определяются различными меню пакета AVR
Studio или кнопками панели инструментов (более подробную
информацию об этом можно найти в меню Help).
Отображение результатов работы программы в симуляторе
производится в окне "Workspace" переключением в режим I/O
(рис. 4). В этом окне можно отображать содержимое всех
регистров и ячеек памяти микроконтроллера. При использова-
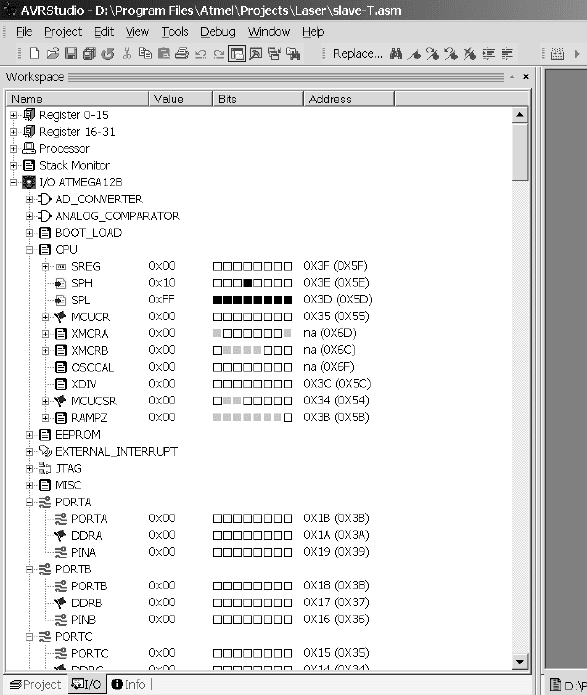
1
1
5
5
нии пошагового режима выполнения программ на любом этапе
можно производить изменение данных вводом с клавиатуры
Рис. 4. Окно I/O
РС новых значений в двоичном, шестнадцатеричном или деся-
тичном формате. Аналогичные операции можно выполнять с
помощью окон "Watch", формируя в этих окнах произвольный и
более удобный для работы с программой набор отображаемых
элементов микроконтроллера.
1
1
6
6
После проверки корректности программы симулятором
можно с помощью программатора произвести запись подготов-
ленного Hex–файла в память микроконтроллера. Необходимо
учитывать, что симулятор не позволяет моделировать все необ-
ходимые функции. Окончательное тестирование программы
может проводиться только на лабораторном стенде с микрокон-
троллером.
Для записи подготовленного Hex–файла в микроконтроллер
необходимо подключить лабораторный стенд к COM-порту
компьютера (в стенде используется разъем DB15F c надписью
AVR studio Prog), подключить стенд к сети 220В и включить
питание. После включения стенда программатор AVR Studio
может работать, его запуск производится из меню Tools пунк-
том AVR Prog. Управление программатором производится в
открывшемся после запуска окне AVRprog на рабочем поле.
В окне программатора необходимо выбрать записываемый
в микроконтроллер Hex–файл (кнопка Browse, файл после ком-
пиляции находится в папке проекта, с которым Вы работаете). В
строке Device выбрать тип микроконтроллера (AT90S8515) и
запустить программатор в режиме программирования флэш-
памяти программ кнопкой Program в области Flash окна про-
грамматора. Для управления программированием ППЗУ в окне
программатора предусмотрена область EEPROM. Устройство
начинает работать сразу после завершения программирования.

1
1
7
7
ЛАБОРАТОРНАЯ РАБОТА № 1
1. ИССЛЕДОВАНИЕ АЛГОРИТМОВ
ВВОДА - ВЫВОДА АНАЛОГОВЫХ СИГНАЛОВ
В МИКРОКОНТРОЛЛЕРАХ
Цель работы: Исследование влияния временных характеристик
сигналов и интервала дискретизации на характе-
ристики преобразования аналоговых сигналов.
Преобразование аналоговых сигналов в цифровой формат
для обработки в микроконтроллерах требует выполнения опера-
ций квантования и дискретизации. Характеристики квантования
и дискретизации должны соответствовать параметрам аналого-
вых сигналов, иначе возникают их недопустимые искажения,
что приводит к получению некорректных результатов обработки
этих данных. Стандартные аналого-цифровые преобразователи
(АЦП) выполняют квантование и дискретизацию с равномер-
ным шагом.
Шаг квантования АЦП
Δ
U определяется величиной его
опорного напряжения U
оп
и разрядностью выходного кода n, а
аналоговый сигнал U
вх
и код АЦП N
АЦП
связаны следующим
образом:
Так как N
АЦП
изменяется в диапазоне 0 ÷ (2
n
– 1), то диапазон
изменения U
вх
составляет
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
÷
n
n
U
2
12
0
оп
.
.
П
П
р
р
и
и
этом значениям
аналогового напряжения меньше 0 соответствует код N
АЦП
= 0, а
значениям напряжения больше максимального напряжения –
код N
АЦП
=(2
n
– 1). Следовательно, допустимый диапазон анало-
гового напряжения для корректного преобразования лежит в
этих границах.
Необходимо также учитывать, что погрешность преобразо-
вания сигнала, связанная с шагом квантования
Δ
U, минимальна
при уровнях напряжений, близких к верхней границе, и может
.
2
где,
n
оп
АЦПвх
U
UNUU =Δ∗Δ=
1
1
8
8
недопустимо возрастать вблизи нижней границы. Поэтому шаг
квантования
Δ
U, определяемый величинами опорного напряже-
ния
U
оп
и разрядностью кода n, должен соответствовать требуе-
мому динамическому диапазону сигналов.
Интервал дискретизации T
Д
и временные или частотные
параметры сигналов должны строго соответствовать друг другу.
Причем нарушение этих требований приводит не только к уве-
личению погрешностей преобразования, но и к получению не-
корректных данных.
В соответствии с известной теоремой Котельникова кор-
ректное восстановление сигнала при дискретизации возможно
при получении не менее двух отсчетов за
период изменения
сигнала. Очевидно, что увеличение числа отсчетов кода за пери-
од сигнала, упрощает условия, выполнение которых необходимо
для восстановления сигнала без искажений. Следует иметь в
виду, что величина интервала дискретизации не может опреде-
ляться только параметрами сигналов, она также зависит от вре-
мени выполнения алгоритмов преобразования данных, от быст-
родействия АЦП, от временных параметров алгоритмов преоб-
разования данных, например, постоянной времени численного
интегрирования и других факторов.
На рис. 5-8 показаны временные диаграммы и спектры си-
нусоидальных сигналов после квантования и дискретизации при
различных соотношениях частоты сигналов (f
ВХ
) и частоты дис-
кретизации (f
Д
= 1/T
Д
). Очевидно, что входной сигнал содержит
единственную спектральную составляющую частотой f
ВХ
, а в
результате преобразования в спектре выходного сигнала появ-
ляются дополнительные спектральные составляющие.
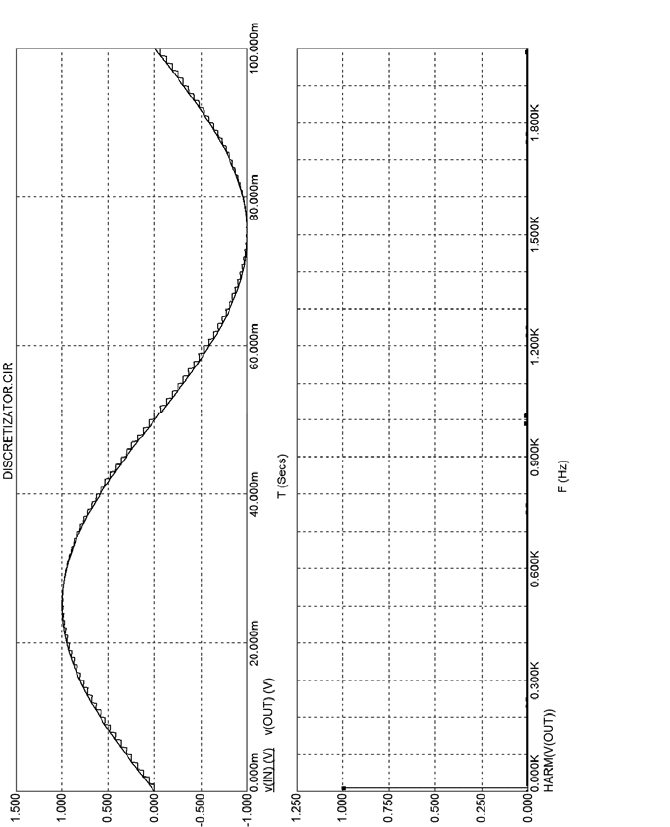
При
ДВХ
f<<f (рис. 5) искажения незначительны, основная
спектральная составляющая частотой f
ВХ
, показанная на спек-
тральной характеристике (рис. 5) в области низких частот, имеет
амплитуду, близкую к входной. Дополнительные спектральные
составляющие вблизи частоты дискретизации f
Д
очень малы.
1
1
9
9
Рис. 5. Временная диаграмма и спектр сигнала при f
ВХ
<<f
Д
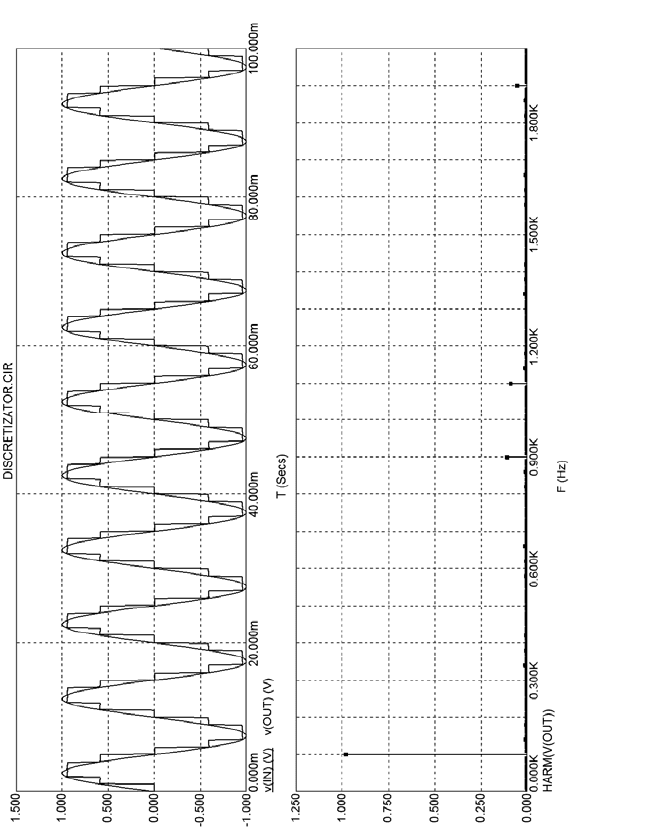
2
2
0
0
Рис. 6. Временная диаграмма и спектр сигнала при f
ВХ
<f
Д
