Ильясов С.Г. Процессы и аппараты упаковочного производства

Подождите немного. Документ загружается.

инженерной практике. На основе материального баланса определяют выход продукта

по сравнению с теоретически возможным (в %), а также количество (массу)

получаемых продуктов в единицу времени. Согласно закону сохранения, масса

(количество) поступающих на переработку веществ \Сд) должна быть равна массе

веществ, получаемых в результате роведения процесса (vga т.е.

В практических условиях при проведении технологического процесса происходят

необратимые потери вещества ]^бд (например, со точными водами или газовыми

выбросами, через неплотности ишаратуры и т.п.), поэтому материальный баланс в

общем случае принимает вид

Для нестационарных процессов материальный баланс имеет несколько иной вид, так

как потоки, направленные внутрь рассматриваемого объема (приход), и потоки,

направленные наружу ^расход), могут быть не равны (например, происходит

накопление массы), т.е.

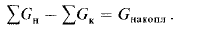
Приход — Расход = Накопление, или

Для стационарных процессов правая часть

выражения (1.5) равна нулю, и без учета потерь

оно приобретает вид уравнения (1.3).

Материальный и энергетический балансы в

макрообъемах (например, в аппарате) при

взаимодействии, например, двух фаз для гепло-

или массопереноса будут зависеть от их

относительного движения. Наиболее

распространенные виды такого относительного

движения потоков (или фаз) представлены на рис.

1-1. При рассмотрении конкретных процессов

тепло- и массопереноса будет показано, что

температуры (для теплопереноса) или

концентрации (для массопереноса) потоков на

выходе из аппаратов могут существенно

различаться, например, для прямоточного (рис. 1-

1, а) и про-швоточного (рис. 1-1,6) движения

потоков при одних и тех же их значениях

(начальных температур и концентраций) на входе

в аппараты. Проиллюстрируем это положение

следующим примером.

Рис. 1-1. Взаимное направление движения

потоков в аппаратах:

а прямоток; ^-противоток

Рассмотрим установившийся процесс поглощения

газа жидкостью (абсорбцию), например

поглощение аммиака водой из аммиачно-

воздушной смеси (рис. 1-2) при условии

отсутствия перемешивания фаз по высоте

аппарата. Количество компонента (аммиака),

переходящего из газовой фазы в жидкую, из

выражения (1.1) определяется как

м == м, = G{y^ - v,) = L(^ - ^),

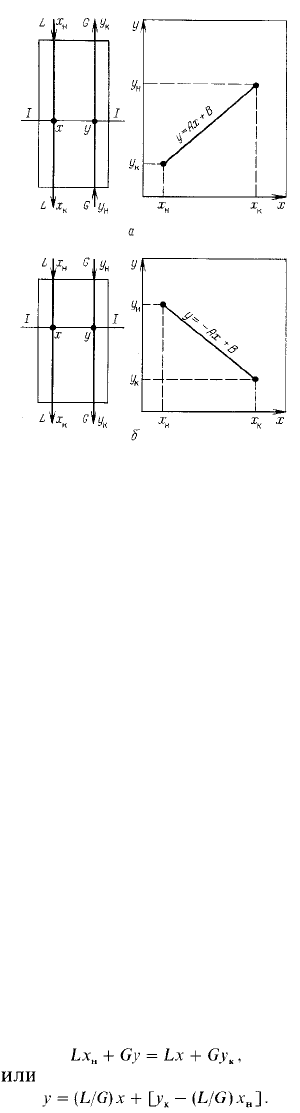
Рис. 1-2. К выводу уравнений материального

баланса и рабочей линии процесса (на примере

абсорбции):

а противоток; б - прямоток

где G и L-расходы соответственно инертного газа

и жидкости, кмоль/с; у^ и \\ - концентрации

компонентов газа на входе в аппарат и выходе из

него, кмоль/кмоль инертного газа; -v„, х^ -

концентрации компонента в жидкости на входе в

аппарат и выходе из него, кмоль/кмоль инертной

жидкости.

Для того чтобы получить связь между текущими

концентрациями в фазах, запишем материальный

баланс для верхней части аппаратов (сечение 1-1,

рис. 1-2, а):

Поскольку L/G == const, а второй член правой части уравнения (1.7) также является

постоянной величиной, получим

где А = L/G -тангенс угла наклона прямой линии; .о—отрезок, отсекаемый на оси

ординат прямой линией.

Уравнение (1.8) описывает связь рабочих концентраций компонента в потоках, обычно

его называют уравнением рабочей линии.

Для прямоточного движения потоков уравнение рабочей линии получают по аналогии

с предыдущим случаем:

Уравнение (1.9) отличается от (1.8) знаком перед коэффициентом А. На рис. 1-2,д и 1-

2,6 построены линии рабочих концентраций по уравнениям (1.8) и (1.9), которые в

дальнейшем, после рассмотрения условий равновесия систем (гл. 2), позволят подойти

к определению движущих сил процессов переноса массы.

1.2. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ

Из первого закона термодинамики может быть сформулировано выражение закона

сохранения энергии: внутренняя энергия U изолированной от внешней среды системы

постоянна, т. е. U = const.

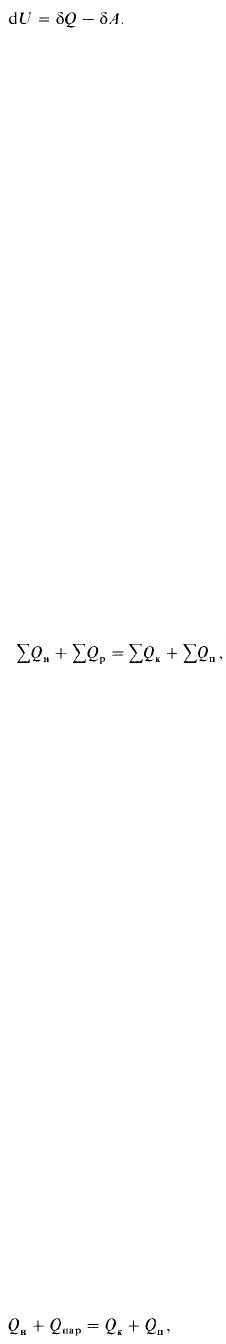
i огда

В уравнении (1.10) величины теплоты SQ и производимой рабо-i i»i 8 А характеризуют

не систему, а процессы ее взаимодействия i окружающей средой, поэтому они не

являются полными дифференциалами. Переход системы из одного энергетического

состояния ц другое характеризуется новым значением внутренней энергии I/, sbk как U

меняется на определенную величину независимо от пути перехода.

Уравнение (1.10) без большой ошибки может быть использовано н качестве закона

сохранения теплоты.

Энергетический баланс. При анализе и расчете химико-техно-югических процессов

часто необходимо определить расход энергии па его проведение, и в частности,

теплоты. Чтобы определить расход теплоты, составляют тепловой баланс как часть

общего щергетического баланса. Тепловой баланс составляют для многих процессов,

протекающих в реакторах, теплообменных аппаратах, массообменных аппаратах

(перегонка жидкостей, сушка и т.п.).

По аналогии с материальным балансом тепловой баланс в общем виде выражается

следующим образом:

; ic \Q^ теплота, вводимая в аппарат с исходными материалами; ^Qp тепловой >ффект

физических и химических превращений; ^бк теплота, выводимая из аппарата

продуктами; ^бп потери теплоты в окружающую среду.

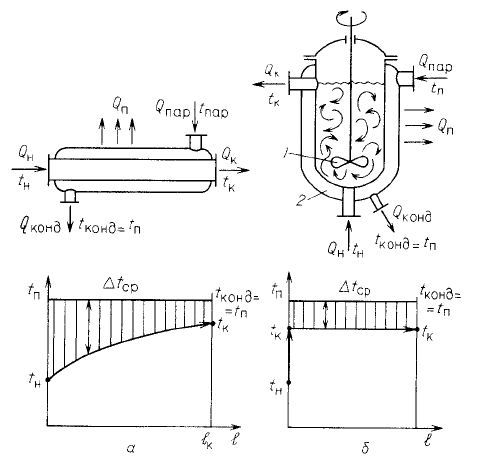
На рис. 1-3 приведены примеры нагревания жидкости в аппаратах идеального

вытеснения и идеального смешения. В аппарате идеального вытеснения температура

жидкости плавно изменяется по длине аппарата / от начальной ^ до конечной ^, так как

текущие н аппарате объемы жидкости вытесняют друг друга, не смешиваясь. 1^

аппарате идеального смешения поступающая жидкость прак-гически мгновенно

смешивается с находящейся в аппарате, поэтому начальная температура /ц жидкости в

таком аппарате мгновенно изменяется до конечной ^.

Средняя разность температур At^p при условии сохранения начальных температур

нагреваемой жидкости ^ и греющего пара t^ (средняя движущая сила процесса) в

аппарате идеального вытеснения выше, чем в аппарате идеального смешения.

Следовательно, н количество переданной при этом теплоты в аппарате идеального

вытеснения больше, т.е. бк.выт > бк.смеш-

Тепловой баланс для обоих случаев идентичен:

но значения величин, входящих в уравнение (1.12), различны. Поэтому при

составлении тепловых балансов часто приходится принимать модель, по которой

работает данный аппарат (идеальное вытеснение, идеальное смешение и т. д.-см. гл. 5),

что приводит

Рис. 1-3. Изменение температуры при нагревании жидкости в аппаратах идеального

вытеснения (а) и идеального смешения (о):

а-двухтрубный теплообменник; б -аппарат с мешалкой (7) и паровой рубашкой (2)

к определенной ошибке, так как работа реального аппарата может отличаться от

работы принятой модели.

Помимо расхода теплоты, энергетический баланс позволяет определить расходы

кинетической и потенциальной энергии на проведение процесса (перемещение

жидкостей, сжатие и транспортирование газов и др.).

1.3. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

Закон сохранения импульса (количества движения) является общим выражением

первого закона термодинамики [уравнение (1.10)] для контрольного объема (см. рис. 1-

1). Импульс по определению равен произведению массы выделенного элемента

жидкости т на вектор скорости его движения н

; следовательно, импульс mw-тоже век-

тор. Поэтому закон сохранения импульса можно представить и в векторной форме, и в

скалярной-в виде трех скалярных уравнений в направлениях осей координат х, у, z.

Баланс количества движения (или импульса) будет рассмотрен в гл. 3 при выводе

основных уравнений движения потока.

Подробнее балансы субстанций (массы, энергии и импульса) будут рассмотрены далее

при анализе и расчете конкретных процессов тепло- и массопереноса.

'РОСЫ ДЛЯ САМОКОНТРОЛЯ

выразите закон сохранения массы для системы, состоящей из ч)иого компонента, и для

многокомпонентной системы. Что понимают под плотностью конвективного потока?

Но каким признакам разделяют материальные балансы? Приведите выражения

материальных балансов для стационарных :( нестационарных процессов. Что

понимают под уравнением рабочей линии? Приведите выражение теплового баланса

аппарата.

ГЛАВА 2

ЗАКОНЫ РАВНОВЕСИЯ

(

'ионные положения закона термодинамического равновесия в системах

рассматриваются в курсах физической химии и термо-

..тамики. Поэтому в данном разделе основное внимание уделено ц; пменению этих

законов для решения инженерных задач-опре-

| гению направления и движущей силы процессов химической \пологий.

Обычно химико-технологические процессы осуществляются при шмо действии фаз.

Контакт между фазами может быть непосред-

. пенным (большинство процессов переноса массы) или через раз-'яющую стенку

(большинство процессов переноса энергии-и юты).

< )сновная задача химико-технологического процесса состоит поправленном

(заданном) изменении макроскопических свойств иствующих в этом процессе

веществ: состава, агрегатного со-ояпия, температуры, давления. Для этого на систему

воздейст-|о1 подачей или отводом теплоты, внешними силовыми полями ,);|

витационными, центробежными и др.), перемещением под исгвием силы давления и

т.п., что приводит к переносу субстан-

• .ш энергии, массы, импульса. Предельным состоянием системы , 1яется подвижное

равновесие, которое не приводит к изменению

' |кроскопических свойств участвующих в процессе веществ во

рсмени и пространстве. Таким образом, равновесным называют !кое состояние

системы, при котором перенос субстанций от-

ствует.

S УСЛОВИЯ ТЕРМОДИНАМИЧЕСКОГО РАВНОВЕСИЯ

. ювия равновесия в процессах переноса теплоты (теплового ишовесия) определяют

сравнительно простыми измерениями тем-' ратур соприкасающихся фаз (см.,

например, рис. 1-3). Механи-\ кое равновесие (при переносе импульса) обнаруживают

по равен-

ству непосредственно измеренных давлений в соприкасающихся фазах. Намного

сложнее определение условия равновесия системы в процессах переноса массы.

Поэтому здесь данному виду равновесия будет уделено основное внимание.

Процесс перехода массы из одной фазы в другую в изолированной замкнутой системе,

состоящей из двух или большего числа фаз, возникает самопроизвольно и протекает до

тех пор, пока между фазами при данных условиях (температуре и давлении)

установится подвижное фазовое равновесие. Оно характеризуется тем, что в единицу

времени из первой фазы во вторую переходит столько же молекул компонента,

сколько из второй в первую (т. е. преимущественного перехода вещества из одной

фазы в другую нет). Достигнув состояния равновесия, система может находиться в нем

без количественных и качественных изменений сколь угодно долго, пока какое-либо

внешнее воздействие не выведет ее из этого состояния. Таким образом, состояние

изолированной системы при равновесии определяется только внутренними условиями.

Поэтому градиенты интенсивных параметров и соответствующие им потоки должны

быть равны нулю:

где Т температура; Р давление; ц, химический потенциал i-го компонента.

Выражения (2.1)-(2.3) называют условиями соответственно термического,

механического и химического (материального) равновесия.

Все самопроизвольные процессы протекают в направлении достижения равновесия.

Чем в большей степени состояние системы отклоняется от равновесия, тем выше

скорость процесса переноса субстанций между фазами вследствие увеличения

движущей силы, обусловливающей этот процесс. Поэтому для осуществления про-

цессов переноса субстанций необходимо не допускать установления состояния

равновесия, для чего к системе подводят вещество или энергию. На практике в

открытых системах это условие обычно реализуется путем создания относительного

движения фаз в аппаратах с противоточной, прямоточной или другими схемами дви-

жения потоков.

Из второго закона термодинамики следует, что в самопроизвольных процессах

энтропия S системы возрастает и в условии равновесия достигает максимального

значения, т. е. в этом случае

Уравнение (2.4), а также уравнения (2.1)-(2.3) определяют условие равновесия

системы.

Химический потенциал в выражении (2.3) определяется как приращение внутренней

энергии U системы при добавлении к системе бесконечно малого количества молей г-

го компонента, отнесенное к этому количеству вещества, при постоянных объеме F,

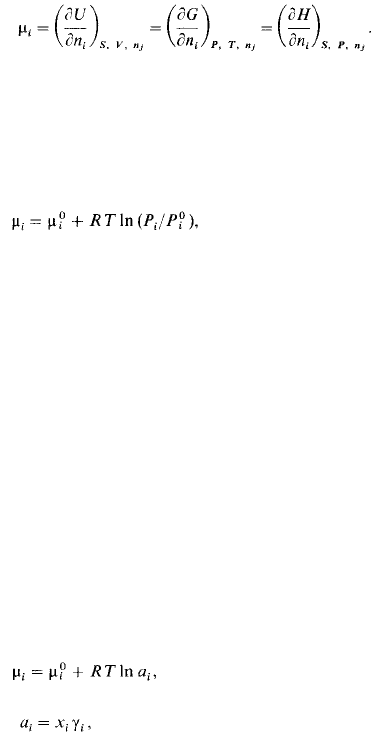
ропии S и количествах молей каждого из остальных компонен-' .^ (где п^= 1, 2, 3, ...).

\\ общем случае химический потенциал может быть определен к приращение любого

из термодинамических потенциалов систе-| при различных постоянных параметрах:

энергии Гиббса G -при '.чоянных давлении Р, температуре Г и п^ энтальпии Я-при ^

юянных S, Р и rij. 1 а ким образом,

Химический потенциал зависит не только от концентрации i итого компонента, но и от

вида и концентрации других компот-шов системы. Для смеси идеальных газов ц^.

зависит лишь от • чщентрации рассматриваемого компонента и температуры:

' р^' значение ц, при стандартном состоянии (обычно при Р, == 0,1 МПа), зависит ii>Ko

от температуры; /^.парциальное давление i-го компонента смеси; Р° -давле-| /1о

компонента в стандартном состоянии.

Химический потенциал характеризует способность рассматри-згмого компонента к

выходу из данной фазы (испарением, крис-| i шзацией и т.п.). В системе, состоящей из

двух и более фаз, ' |к'ход данного компонента может происходить самопроизвольно

"и*ко из фазы, в которой его химический потенциал больше, ф.пу с меньшим

химическим потенциалом. В условиях равновесия имический потенциал компонента в

обеих фазах одинаков.

В общем виде химический потенциал может быть записан юдующим образом: