Ильясов С.Г. Процессы и аппараты упаковочного производства

Подождите немного. Документ загружается.

к (у, активность г-го компонента смеси; х^ и у ^соответственно мольная доля . коэффициент

активности /-го компонента.

Коэффициент активности у^. является количественной мерой i к-я; дальности поведения i-ro

компонента в смеси. При у^ > 1 i клонение от идеального поведения называют положительным, •рп у,<

1 -отрицательным. Для отдельных систем у( ^ 1. Тогда \\, и уравнение (2.7) принимает вид

Для идеальных систем химический потенциал можно выразить .и<же с помощью летучести/,

компонента:

;< / ° летучесть /-го компонента в стандартных условиях.

Значения величин а^ и /^ находят в справочной литературе. При проведении технологических

процессов рабочие среды (газ, '.ip, жидкость) находятся в неравновесном состоянии, которое не

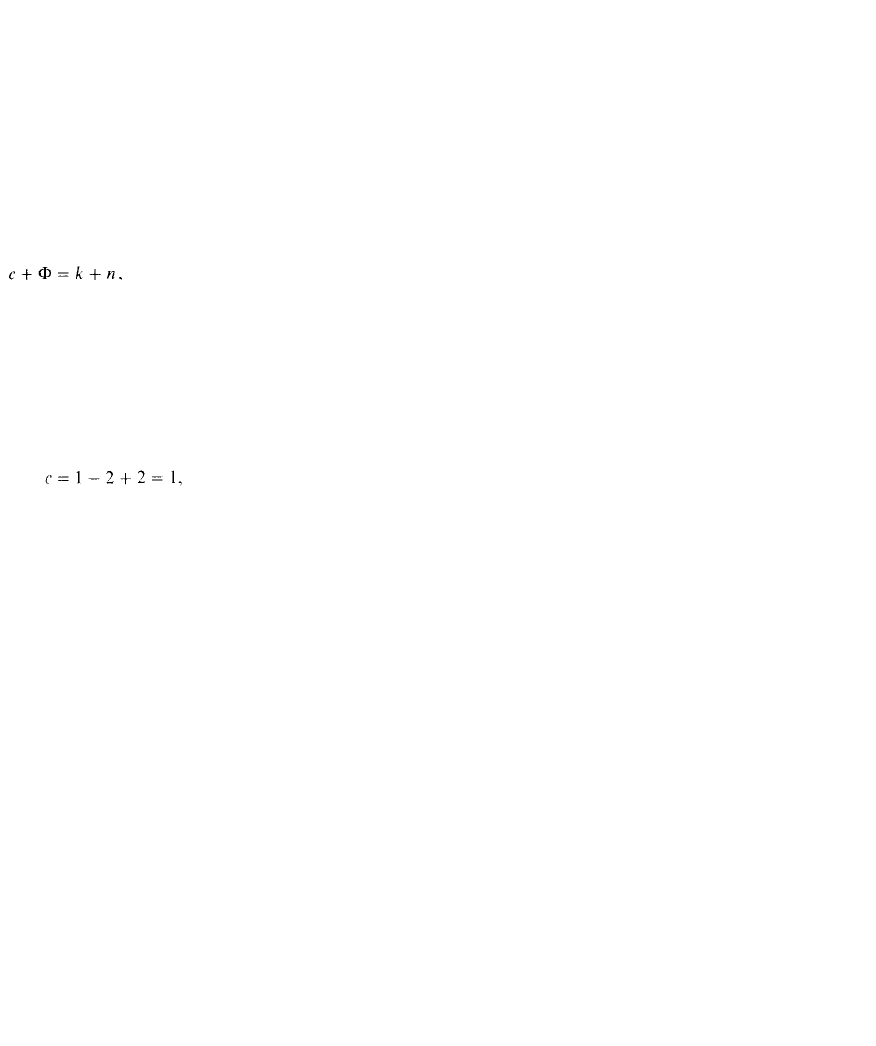
может быть описано термодинамическими параметрами. Для описания неравновесного состояния

систем вводят дополнительные неравновесные, или диссипативные, параметры, в качестве которых

используют градиенты интенсивных термодинамических величин -температуры, давления,

химического потенциала и плотности соответствующих диссипативных по токов, связанных с

переносом энергии, массы и импульса.

2.2. ПРАВИЛО ФАЗ

Существование данной фазы в системе или равновесие фаз возможны лишь в определенных

условиях. При изменении этих условий равновесие системы нарушается, происходит с двиг фаз или

перехо д вещес тва из одной фазы в другую. Возможное существование данной фазы в равновесии с

другими определяется правилом фаз, или законом равновесия фаз Гиббса'.

где с- число степеней свободы (давление, температура, концентрация)-минимальное число параметров, которые можно

изменять независимо друг от друга, не нарушая равновесия данной системы; Ф число фаз системы; k число независимых

компонентов системы; п -число внешних факторов, влияющих на положение равновесия в данной системе.

Для процессов переноса массы п == 2, так как внешними факторами в этом случае являются

температура и давление. Тогда выражение (2.11) принимает вид с + Ф = k + 2. Отсюда с == k — -Ф+2.

Таким образом, правило фаз позволяет определить число параметров, которое можно менять, не

нарушая фазового равновесия системы.

Например, для однокомпонентной равновесной системы жидкость-пар число степеней свободы

т. е. в этом случае произвольно может быть задан только один параметр-давление или температура.

Таким образом, для одно компонентной системы имеется о днозначная зависимость между

температурой и давлением в условиях равновесия. В качестве примера можно привести широко

распространенные справочные данные-зависимости между температурой и давлением насыщен ных

паров воды.

Для однокомпонентной равновесной системы, состоящей из трех фаз (твердое тело-жидкость-

пар), число степеней свободы равно нулю: с = \ — 3+2=0. Например, система вода-лед-водяной пар

находится в равновесии при давлении 610,6 Па и температуре 0,0076 °С.

Для двухкомпонентной равновесной системы жидкость - пар число степеней свободы с==2—

2+2=2.

В этом случае одной из переменных величин (например, давле

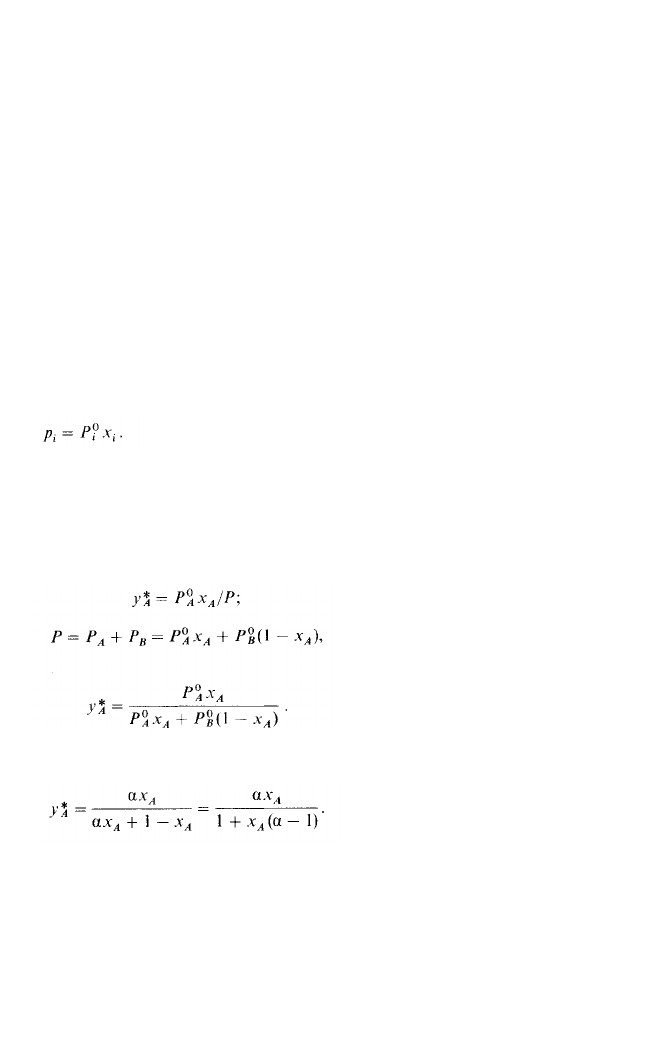
растворимость газа снижается; с увеличением общего давления значение т

снижается, что приводит к увеличению растворимости

газа.

При постоянных температуре и давлении зависимость между

равновесными значениями у и рабочими х выражается графически прямой

линией, проходящей через начало координат, с у глом наклона, тангенс

которого равен w.

Закон Генри точен для идеальных растворов. Для реальных рас творов он

применим с достаточной точностью только при сильном разбавлении. Для

хорошо растворимых газов при больших концентрациях их в растворе

растворимость меньше, чем следует из закона Генри. Для систем, не

подчиняющихся э тому закону, значе ние т в уравнении (2.16) являе тся

переменной величиной, и линия равновесия представляет собой кривую,

которую строят обычно по опытным данным.

Если температура идеального раствора ниже критической температуры

газа, т. е. происхо дит конденсация газа, то система подчиняется закону

Рауля, который можно получить, сопоставив выражения (2.6) и (2.9) при

условии равенства химических потенциалов:

Из выражения (2.17) следует, ч то парциальное давление пара i-го

компонента над раствором равно произведению давления пара чистого

компонента (т. е. давления насыщенного пара этого компонента) при

температуре раствора на его мольную долю в жидкой фазе. Для

дву хкомпонентной смеси состава А-В выражения (2.15) и (2.17) дают связь

между рабочими и равновесными концентрациями:

Поделив последнее выражение на Р^ и обозначив Р^/Рв через а (где а -

относительная летучесть компонентов), получим

Это уравнение является уравнением кривой линии. Отметим, что

коэффициенты относительной летучести мало изменяются с изме нением

температуры и снижаются при увеличении давления в систе ме, что приводит

к уху дшению условий разделения смеси.

Если для данной системы закон равновесного распределения вещества

между фазами неприменим, то эту зависимость можно найти по

справочникам и построить соответствующую кривую на фазовой диаграмме.

Чаще приходится пользоваться эксперимен-

3.2. ОСНОВНОЕ УРАВНЕНИЕ ПЕРЕНОСА СУБСТАНЦИЙ

Выделим в жидкости, находящейся в движении, произвольный объем V,

ограниченный поверхностью S. Объем У жидкости расположен в неоднородном поле

физического потенциала переноса (р. Задача сводится к выводу дифференциальных

уравнений, описывающих распределение скоростей, концентраций и температур во

времени и пространстве, что необходимо для решения многих задач гидродинамики,

тепло- и массообмена. Если объемные силы консервативны, т. е. не изменяются во

времени, то их можно заменить потенциалом переноса.

Потенциал переноса представляет собой удельную (отнесенную к единице

объема) массу, энергию или количество движения. В слу чае переноса массы в

качестве потенциала переноса рассматривают плотность (р) или концентрацию (С):

| де т, масса i-го компонента смеси; [р] ==• [С] == [кг/м ].

В случае переноса энергии (теплоты) потенциалом переноса являе тся

энтальпия единицы объема жидкости:

i де Ср теплоемкость среды; [с'рф] = [Дж/м

В гидродинамических процессах потенциалом переноса является

количество движения (импульса) единицы объема жидкости:

В рассматриваемом объеме жидкости существуют источники

потенциала переноса, характеризующиеся у дельной объемной плотностью

притока у, т. е. скоростью притока энергии [у] = = [ДжДм^с)], массы [у] =

[кг/(м

• с)] или импульса [у] = = [кгДм^с)] в единице объема.

Процессы тепло- и массопереноса через рассматриваемую поверхность S

осуществляются двумя видами механизма переноса:

1) молекулярным, т. е. переносом, возникающим в результате стремления

системы к термодинамическому равновесию, отклонения от которого

объясняются неоднородностью поля потенциала; 2) макроскопическим-

коивективным переносом, вызванным наличием поля скоростей жидкости в

объеме V. В случае переноса количества движения (импульса) к указанным

двум видам переноса добавляется также перенос, вызванный наличием поля

гидростатического давления, а при переносе теплоты - перенос за счет

теплового излучения.

Поток субстанции, вызванный стремлением системы к термо-

динамическому равновесию (молекулярный перенос), определяется

хаотическими перемещениями молекул среды, переносящих массу, энергию

и импульс и тем самым усредняющих потенциал в рас сматриваемом объеме.

Молекулярный перенос является определяющим в неподвижных сре дах и в

ламинарно движущихся потоках и описывается следующими известными

линейными градиентными законами.

Для переноса массы - первым законом Фика:

где D коэффициент молекулярной диффузии, м

/c.

Для переноса энергии (теплоты) - законом Фурье:

где \ - коэффициент теплопроводности.

Перепишем уравнение (3.15) с учетом уравнения (3.12):

где а == X/fc'pp) -коэффициент температуропроводности, м/с.

Для переноса импульса (с учетом закона внутреннего трения Ньютона):

где

Перепишем уравнение (3.17) с учетом уравнения (3.13):

Как видно из приведенных законов, выражающих плотность

>ка необратимого переноса массы, энергии и импульса в газах тельных

жидкостях, все они описываются аналогичными урав-

ЕЯМИ. Это связано со сходством физических явлений, лежащих < пове

переноса. Для газов можно говорить о весьма близкой аналогии, по-

1ьку для них значения всех коэффициентов молеку лярного пе-юса

довольно близки: D % а % v. Такая близость свидетельствует юм, что

диффузионный механизм переноса массы, энергии ч м пульса,

являющийся следствием хаотического теплового дви-II! я молекул в

газах, в первом приближении одинаков. Капельные жидкости имеют

различные значения коэффициентов окулярного переноса, поэтому в

данном случае аналогия явле-it переноса носит ограниченный характер. I

а ким образом, молекулярный перенос (плотнос ть потока) мае-

</„( , энергии q^t

импульса q^^ описывается идентичными по

рме уравнениями, которые могут быть обобщены следующим ^.(жением:

А коэффициент пропорциональности, в зависимости от вида переноса прини-'щий значение

D, а или v.

11ри конвективном переносе масса, энергия и импульс транспор-рмотся в

объеме макрочастиц, движущихся со скоростью w.

чпость конвективного по тока q ^ массы, энергии или импульса

каждом участке повер хности можно выразить следующим

•ра'юм:

VS участок поверхности, расположенный перпендикулярно вектору w.

1с1ким образом, в случае молекулярного и конвективного пе-оса массы

или энергии плотнос ть потока q складывается из двух гавляющих:

При анализе процесса переноса теплоты в правую часть урав-

!пя (3.21) следует добавить еще одну величину (^д), учиты-ццую вклад в

общий перенос теплоты теплового излучения. В[>1делим на повер хности

S, ограничивающей произвольный

^см К элемент повер хности dS. Представим его в векторной

ГЛАВА 2 МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

Наиболее перспективный метод решения задач исследования расчета химико-технологических

процессов - теоретический метод, основанный на составлении и решении дифференциальных

уравнений, полностью описывающих процесс (такие уравнения приведены, например, в предыдущей

главе - уравнения переноса массы, энергии и импульса). В частных, упрощенных случаях решения

этих уравнении найдены, некоторые из них приведены ниже (например, решения уравнений Эйлера

для условий равновесия и установившегося движения идеальной жидкости приводят к широко

используемым в инженерной практике основному уравнению гидростатики и уравнению Бернулли).

Дифференциальные уравнения описывают целый класс однородных явлений (например, одним

уравнением - Навье-Стокса - описываются такие разные, на первый взгляд, явления, как

движение жидкости по трубопроводам и каналам и перемещение больших объемов

океанической воды и атмосферного воздуха). Для практического использования этих уравнений

следует при их решении у ч и тывать ограничения, вытекающие из свойств конкретного явления

(процесса). Для химико-технологических процессов такими ограничениями могут быть пределы

изменений геометрических характеристик аппаратов, физических свойств веществ и т.п. Поэт ому

для выделения конкретного явления из класса явлений, описываемых единой системой

дифференциальных уравнений, необходимо эти уравнения ограничить дополнительными

условиями, которые называют условиями однозначности, т.е. условиями, которые полностью,

однозначно характеризуют данное явление (например, температура насыщенного пара

полностью, т.е. однозначно определяется его давлением).

Условия однозначности включают: 1) геометрическую форму и размеры системы

(аппаратуры); 2) физические свойства веществ, у ч а с т вующих в процессе; 3) начальные условия

(начальную скорость, начальную температуру и т.п.); 4) граничные условия (например,

равенство нулю скорости жидкости у стенок трубы).

Однако многие химико-технологические процессы настолько сложны, что удается лишь

составить систему дифференциальных уравнений для их описания и установить условия

однозначности. Решить же эти уравнения известными в математике методами обычно не

представляется возможным. В подобных случаях используют метод моделирования. В широком

смысле под моделированием понимают исследование объектов познания на их моделях, поэтому

моделирование неотделимо от развития знания.

Моделирование находит широкое применение как при проведении научных исследований, так

и при решении большого числа практических задач в различных областях техники: в гидравлике

и гидротехнике (определение конструктивных и эксплуатационных характеристик гидротехнических

сооружений, моделирование течении рек, волн, приливов и отливов и др.); в авиации, ракетной

и космической технике (определение характеристик летательных аппаратов и их двигателей и др.); в

судостроении (определение характеристик корпуса судна и др.); в теплотехнике (при

конструировании и эксплуатации различных тепловых аппаратов) и т.п.

Огромное значение имеет моделирование при исследовании химико-технологических

процессов и проектировании химических производств. При этом под моделированием понимают

метод исследования химико-технологических процессов на моделях, отличающихся от объектов

моделирования (натуры) в основном масштабом. Моделирование можно осуществлять двумя

основными методами - методом обобщенных переменных, или методом теории подобия

(физическое моделирование), и методом численного эксперимента (математическое

моделирование). Принципиального различия между этими методами нет, поскольку оба они в

большей или, меньшей степени основаны на экспериментальных данных и разли чаются лишь

подходом к их обработке и анализу.

2.1 МЕТОД ОБОБЩЕННЫХ ПЕРЕМЕННЫХ

Метод обобщенных переменных составляет основу теории подобии. Одним из основных

принципов теории подобия является выделение из класса явлений (процессов), описываемых общим

законом (процессы движения жидкостей, диффузии, теплопроводности и т. п. группы подобных

явлений.

Подобными называют такие явления, для которых отношения сходственных и

характеризующих их величин постоянны.

Различают следующие виды подобия: а) геометрическое; б) временное; в) физических

величин; г) начальных и граничных условий.

Геометрическое подобие предполагает, что сходственные размеры натуры и модели

параллельны, а их отношение выражается постоянной величиной.

Предположим, что изучается сложное явление - движение газа во вращающемся цилиндре (рис.

4-1). Чтобы исследовать процесс в данном аппарате, строим модель, соблюдая геометрически

подобие (рис. 4-1,6), т.е. равенство отношений сходственных линейных размеров натуры и модели.

Рис. 4-1. К определению условий подобия натуры (а) и модели (б)

Если рассматриваемая система (натура, образец) находится в движении, то при наличии

геометрического подобия все ее точки должны перемещаться по подобным траекториям

сходственных точек подобной ей системы (модели), т. е. проходить геометрически подобные пути

(точки А

и А

). Геометрическое подобие соблюдается при равенстве отношений всех

сходственных размеров натуры и модели:

consta

 ...

Безразмерную величину а

называют константой геометрического подобия, или масштабным

(переходным) множителем. Константа подобия характеризует отношение однородных

сходственных величин в подобных системах (в данном случае - линейных размеров натуры и

модели) и позволяет перейти от размеров одной системы (модели) к другой (натуре).

Временное подобие предполагает, что сходственные точки или части геометрически подобных

систем (натуры и модели), двигаясь по геометрически подобным траекториям, проходят

геометрически подобные пути в промежутки времени, отношение которых является постоянной

величиной:

= τ

/τ

= a

где Т

и Т

— время прохождения сходственными частицами всего аппарата, соответственно

натуры и модели; τ

и τ

- время прохождения сходственными частицами подобных путей l

и l

; а

константа временного подобия.

Подобие физических величин предполагает, что в рассматриваемых подобных системах

(натуры и модели) отношение значений физических величин двух любых сходственных точек или

частиц, подобно размещенных в пространстве и времени, есть величина п о с т о янная.

Например, если в натуре частица за время τ

прошла путь l

(рис. 4-1, а), а в модели - за время τ

путь l

, то для сходственных точек A

и A

имеем

/μ

= а

; ρ

/ρ

= а

, или u

= а

где u

и и

- совокупность физических величин (но в общем случае а

≠ а

≠ a

и т.д.)

Подобие физических величин включает подобие не только физических констант, но и

совокупности значений физических величин, и л и полей физических величин. Таким образом, при

соблюдении геометрического и временного подобия будет соблюдаться также подобие полей

скоростей, температур, концентраций и других физических величин, т.е. w

= a

, t

= a

;

= а

– константы.

Подобие начальных и граничных условий предполагает, что начальное состояние и состояние

на границах систем (натуры и модели) подобны, т.е. отношения основных параметров в начале и на

границах систем постоянны. Это справедливо лишь в тех случаях, когда для начальных и

граничных условий систем выдерживаются и геометрическое, временное и физическое подобия,

т.е. L

= а

; μ

/μ

= а

Этим подчеркивается важность подобия начальных и граничных условий, поскольку иногда в

основном объеме системы подобие милеет соблюдаться не полностью. Вместе с тем даже

незначительное отклонение начальных и граничных условий может привести к существенному

нарушению подобия системы в целом (например, неучет сильных возмущений всей системы

вследствие так называемых «входных эффектов»).

Все константы подобия постоянны для различных сходственных точек подобных систем, но

изменяются в зависимости от соотношения размеров натуры и модели. Иными словами,

отношение однородных сходственных величин для натуры и другой модели также подобной

натуре, будет другим. Это обстоятельство представляет большие неудобства для

масштабирования и преодолевается введением так называемых инвариантов* подобия.

Инварианты подобия и критерии подобия. Если все сходственные величины, определяющие

состояние данной системы (натуры) и подобной ей системы (модели), измерять в относительных

единицах, т.е. брать сходственное отношение величин для каждой системы, то оно также будет

величиной постоянной и безразмерной, например

= L

= ... = inv = idem = i

; T

/τ

= T

/τ

= ... = i

Величины i

, i

и т.д. не зависят от соотношения размеров натуры и модели, т.е. для

другой модели, также подобной натуре, значения i

, i

... будут те же. Таким образом, отношения

геометрических размеров, времени и физических констант в данной системе (натуре) равны

отношениям тех же величин в подобной системе (модели). При переходе от одной системы к

другой, ей подобной, численное значение величин i

, i

, ... сохраняется. Поэтому безразмерные

числа i, выражающие отношение двух однородных величин в подобных системах, носят название

инвариантов подобия.

Инварианты подобия, представляющие собой отношения однородных величин, называют

симплексами**, или параметрическими критериями*** (например, отношение L

геометрический симплекс). Инварианты подобия, выраженные отношением разнородных величин,

называют критериями подобия. Обычно их обозначают начальными буквами имен ученых,

внесших существенный вклад в данную область знания (например, Re-число, или критерий,

Рейнольдса).

Можно получить критерии для любого физического явления. Для этого необходимо иметь

аналитическую зависимость между переменными величинами рассматриваемого явления. Критерии

подобия безразмерны (как и инварианты подобия), их значения для каждой точки данной системы

могут меняться, но для сходственных точек подобных систем не зависят от относительных

размеров натуры и модели.

____________

* invariants (лат.) - неизменяющийся.

** simplex (лат.) - простой.

*** kriterion (греч.) - признак, средство для суждения

Таким образом, явления, подобные между собой, характеризуются численно равными

критериями подобия. Равенство критериев подобия - единственное количественное условие подобия

процессов. Отсюда очевидно, что отношение критериев одной системы к критериям подобной ей

системы всегда равно 1. Например, для натуры и модели Re

= Re

. Тогда

2222

1111



= 1, или

)/)(/)(/(

212121











aaaddww

Если отношение констант подобия равно 1, оно носит название индикатора подобия и