Ильясов С.Г. Процессы и аппараты упаковочного производства

Подождите немного. Документ загружается.

жидкость смывают порции жидкости, уже прореагировавшей с газом чаром), т.е.

каждый элемент поверхности жидкости взаимодействует газом (паром) в течение

некоторого времени т (время контакта ' |и обновления), после чего данный

элемент обновляется. На •гнове этой модели, принимая время т контакта

постоянным для vcex элементов поверхности, Хигби получил уравнение для

опре-

деления коэффициента массоотдачи:

Как следует из уравнения (15.23), в отличие от пленочной модели скорость

переноса по пенетрационной модели, как и по модели диффузионного

пограничного слоя, М - D

, что подтверждается экспериментом.

Как и Хигби, Кишиневский принимает время контакта постоянным; за время

контакта перенос вещества происходит посредством как молекулярной, так и

турбулентной диффузии и описывается уравнением (15.23), причем коэффициент

молекулярной диффузии D в уравнении (15.23) заменяется на сумму

коэффициентов молекулярной и турбулентной диффузии, обозначаемую D^ .

Предложены и другие модели механизма массопереноса. Следует отметить, что

их приведенные выше модели можно использовать для расчета процессов только

в частных случаях, так как вследствие чрезвычайной сложности турбулентных

двухфазных потоков практически невозможно определение в них поверхности

контакта фаз, распределения концентраций в фазах и других параметров,

необходимых для расчета.

5.1.4 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРЕНОСА МАССЫ

Для вывода уравнений конвективного переноса массы воспользуемся основным

уравнением переноса субстанций [уравнение (3.27)]:

где (р -потенциал переноса массы; <у-плотность потока массы; у-источник

переноса массы (принимаем, что у = 0, так как дополнительный подвод массы к

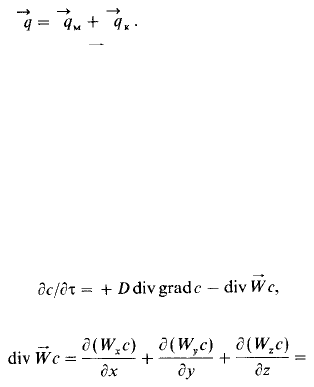
потоку отсутствует).

В процессах массопередачи потенциалом переноса является концентрация, и

поэтому 3(р/3т_^ дс/дх.

Плотность потока массы q складывается из двух составляющих:

В уравнении (15.24) величина q^ = -D grade отражает плотность молекулярного

переноса массы [первый закон Фика, уравнение (3.14)], а ^ = We- плотность

конвективного потока массы.

Тогда основное уравнение переноса субстанции применительно к процессу

переноса массы запишется следующим образом:

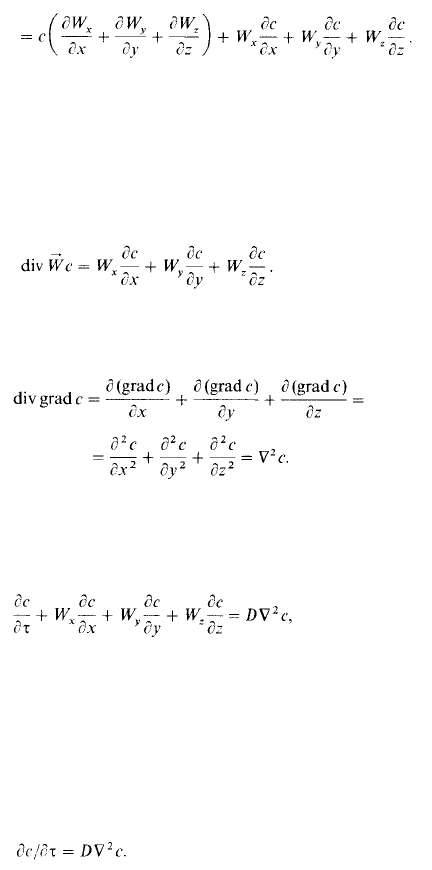
Поскольку при условии неразрывности потока величина

\\'\1дх} + (д\Уу/с1у) + (BWJQz} = 0, то уравнение (15.25) принимает

-I \

В уравнении (15.25) значение div grade выражается как

Таким образом, после проведенных преобразований уравнение I ^ 25)

обращается в дифференциальное уравнение (3.46) конвек-и иной диффузии:

юрое выражает в общем виде распределение концентрации • -мпонента в

движущемся потоке при неустановившемся процессе 'ссопереноса.

При массопереносе в неподвижной среде И^ = W^ = W^ = 0, и ' лвпение (3.46)

примет следующий вид:

Уравнение (15.29) называют дифференциальным уравнением мо-кхлярной

диффузии, или вторым законом Фика. Оно описывает (определение

концентраций вещества в неподвижной среде моле-|ярной диффузией.

Отметим, что уравнение конвективной диффузии, поскольку ;ч>цесс переноса

массы протекает в потоке, должно быть допол-ио уравнениями движения

Навье-Стокса и неразрывности ножа. Кроме того, перенос вещества приводит к

изменению состава ! \ и, следовательно, к изменению их физических свойств.

Поэтому ктему дифференциальных уравнений, описывающих конвектив-мй

массоперенос, следует дополнить также уравнениями, отра-нощими

зависимость физических свойств фазы от ее состава. ючет такой системы

уравнений представляет большие трудности, аналитическое решение этой

системы уравнений оказывается тактически целесообразным только в тех

случаях, когда возможны щественные ее упрощения. Поэтому часто для

решения этой i лачи используют методы теории подобия.

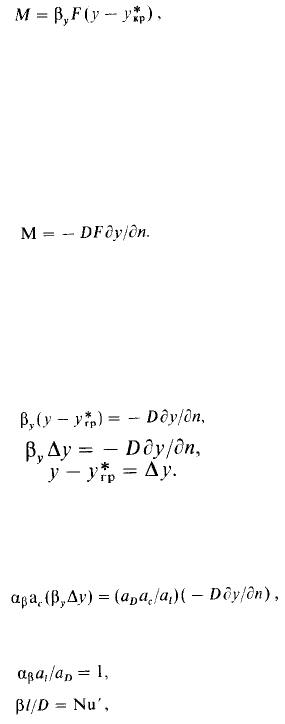
5.2 ПОДОБИЕ МАССООБМЕННЫХ ПРОЦЕССОВ

Общность дифференциальных уравнений теплообмена (3.40) и массообмена

(15.25) позволяет полагать, что основные критерии массообменных процессов

должны быть аналогичны основным

критериям теплообмена.

Рассмотрим уравнения массопереноса на границе раздела фаз.

Из одной фазы в другую переходит количество массы, равное

где J*p равновесная концентрация на границе раздела фаз.

Это же количество массы переносится молекулярной диффузией через

пограничный слой:

В этих уравнениях трудноопределимы величины уТр и ^-толщина

пограничного слоя, через который проходит вещество молекулярной диффузией.

Отсюда

Перемножим на масштабные множители каждый член последнего уравнения:

где /-определяющий геометрический размер.

Данный безразмерный комплекс является аналогом теплового критерия

Нуссельта (Nu == а//Х,) и называется поэтому диффузионным критерием Нуссельта

(иногда - критерием Шервуда Sh). Критерий Нуссельта Nu' является определяемым

критерием, поскольку в него входит величина Р. Так как Nu' — P/D, то Nu'

характеризует отношение скорости переноса вещества (конвективного и молеку-

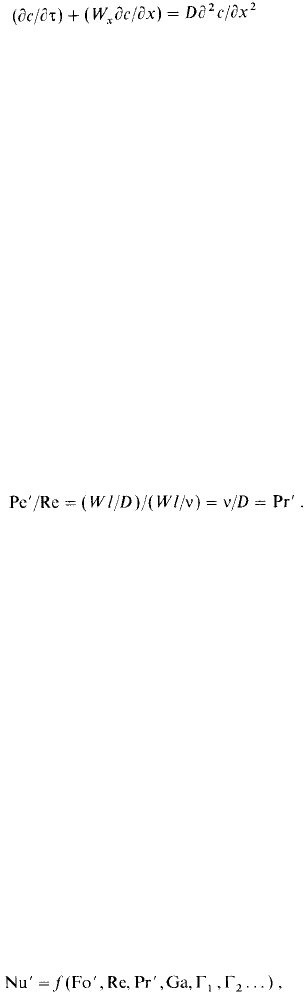
лярного-?) к молекулярному переносу (D).

Другие критерии массообменных процессов получим из дифференциального

уравнения конвективной диффузии (15.25). Переписав уравнение (15.25)

относительно оси х:

и проведя его подобное преобразование, получим следующие критерии

подобия:

Ф rD//

= Fo'-диффузионный критерий Фурье (аналог теплового критерия

Фурье Fo == Тй//

), который характеризует подобие неустановившихся процессов

массообмена;

WI/D == Ре'-диффузионный критерий Пекле (аналог теплового ;перия Пекле Р

== Wl/a).

Критерий Ре' ^ W/D характеризует отношение переноса ве-. ива конвекцией

(W) к молекулярному переносу (D) в сходст-ппых точках подобных систем. Часто

критерий Ре' заменяют ношением

Диффузионный критерий Прандтля Рг' является аналогом теп-ного критерия

Рг = у/а (иногда критерий Рг' называют критерием Пмидта Sc).

Формально критерий Рг' выражает постоянство отношения фи-гчсских

свойств жидкости или газа в сходственных точках подоб-

ч.1\ систем. По существу

же критерий Рг' характеризует отношение цофиля скоростей (через v) к профилю

концентраций (через D), т. е. ношение толщины гидродинамического и

диффузионного погра-

1 шых слоев.

Для соблюдения подобия процессов массоотдачи необходимо .к же

соблюдение гидродинамического подобия. Поэтому крите-s и лльное уравнение

массоотдачи для неустановившегося процесса • ют иметь следующий вид (Г -

геометрический симплекс-см. 5^:

При установившемся процессе и при отсутствии влияния сил

/к сети (т.е. при Fo' -=- 0 и Ga == О):

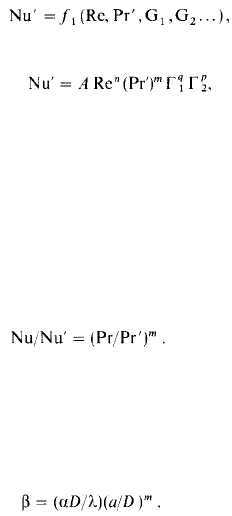
^ п, w, <7, p определяют опытным путем.

Уравнение (15.30) является обобщенным критериальным урав-инем

массоотдачи. Поскольку оно аналогично критериальному 1.}внению теплоотдачи

(11.35,а), то при одинаковых гидродина-'> носких условиях

С помощью выражения (15.31) можно найти соотношение между

»)ффициентами тепло- и массоотдачи:

чорое позволяет по известному значению, например а, опреде-;пь величину

коэффициента массоотдачи ? при одних и тех же | фодинамических условиях.

5.3 ДВИЖУЩАЯ СИЛА МАССООБМЕННЫХ ПРОЦЕССОВ

В соответствии со вторым законом термодинамики состояние замкнутой

системы при взаимодействии двух фаз стремится к равновесию (см. гл. 2), что

характеризуется равенством химических потенциалов компонентов фаз. Движущей

силой переноса массы при этом является разность химических потенциалов того или

иного компонента. Как отмечалось в гл. 2, поскольку химические потенциалы

неидеальных систем определить достаточно сложно, то при анализе и расчете

процессов массопереноса обычно рассматривают изменение не химических

потенциалов, а концентраций компонентов, определение которых значительно

проще.

Обычно начальные и конечные рабочие концентрации заданы или

определяются по уравнению материального баланса. Изменение рабочих

концентраций по поверхности массообмена описывается уравнением рабочих линий.

Эти линии используют для определения движущей силы процесса по всей

поверхности F мас-сопередачи, а также для определения высоты Н массообменных

аппаратов.

Процесс массопереноса протекает самопроизвольно при наличии разности

между рабочими и равновесными концентрациями (при данных условиях

температуры и давления), которые можно выразить через концентрации у и у * фазы

Фу, а также х и х * для фазы Ф^.

Разность между рабочими и равновесными концентрациями и есть

движущая сила массообменных процессов.

Движущую силу в концентрациях фазы Фу будем выражать так:

А^ = у — у* (при у > у*) или А^ == у* — у (при у < j.'*), а в концентрациях

фазы Ф^ — Ах = х — х* или Ах = х* — х.

Таким образом, движущая сила характеризует степень отклонения системы

от равновесия. При установлении равновесия между фазами массообмен между

ними прекращается.

Так же как и при теплообмене, величина движущей силы массообменных

процессов зависит от относительного направления движения фаз (противоток,

прямоток и др.) Кроме того, на движущую силу большое влияние оказывает

гидродинамическая структура потоков.

Рассмотрим вариант, когда в массообменном аппарате фазы движутся

противоточно по отношению друг к другу, аппарат работает в стационарном режиме

по модели МИВ (рис. 15-4, а). Полагаем, что перенос вещества происходит из фазы

Ф^ в фазу Фу, т. е. у < у* . Для этого случая линия равновесия располагается выше

линии рабочих концентраций (рис. 15-4,6).

Для каждой точки или сечения аппарата А^ == ^* — у, т.е. получим aj^ , А^2

и т. д. Для этого же варианта движущую силу выразим в концентрациях фазы Ф^

(рис. 15-4, б). Тогда Лх=х—х*, т.е. Лх^ == х^ — хТ, Лл-з и т. д.

Отсюда видно, что движущая сила изменяется с изменением

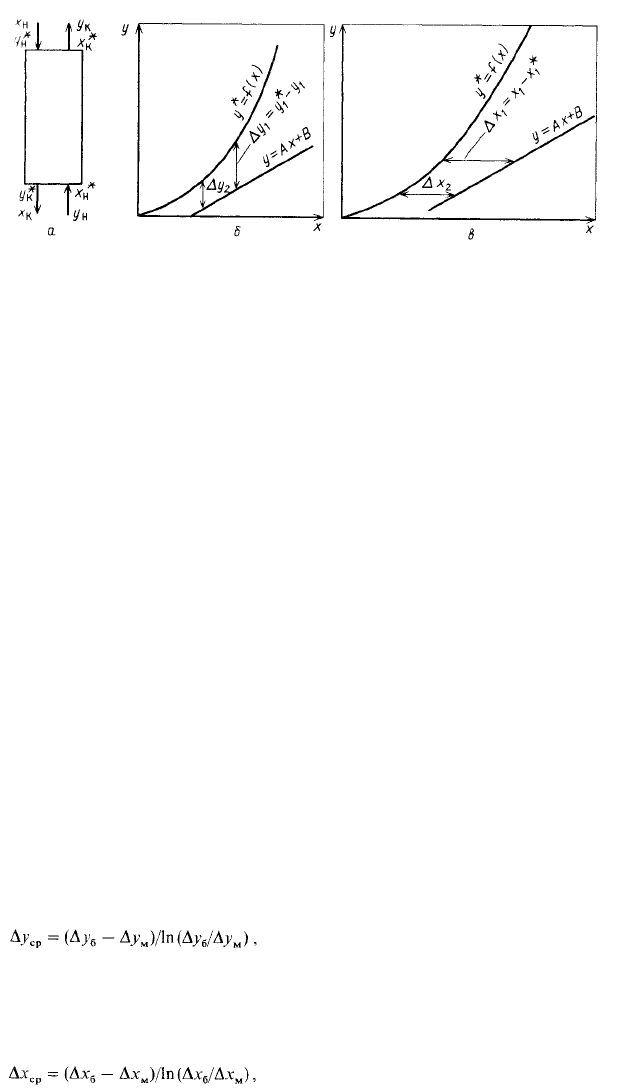
I • 15-4. К пояснению выражения движущей силы противоточного процесса '

' < ^передачи:

ма потоков в противоточном массообменном аппарате; б, в-выражение

движущей силы ' " "обменных процессов в концентрациях фаз соответственно Фу и

Ф^

I > ючей концентрации. Поэтому для всего процесса (или для всей ' ксрхности

F массопередачи) должна быть найдена средняя дви-

• щ11я сила. Для упрощения выводов полагаем, что аппарат рабо-!* 1 по

противоточной схеме при идеальном вытеснении, линия I ншовесия прямая (т.е. у^ =

wx), m>l и перенос вещества-из |i '>!»i Ф^ в фазу Фу (рис. 15-5).

Хпалогичная задача рассматривалась в гл. 11 при выводе дви-

• '.щей силы процессов теплопереноса. Поэтому по аналогии с

. юпереносом можно написать для массопереноса следующее | ражение

движущей силы процесса А^р в концентрациях фазы /' (рис. 15-5,а):

« ея фазы Ф^ (рис. 15-5,6)-

\г„ и Axg-большая, а А^^ и А.х^- меньшая разности концентраций на концах

'^обменного аппарата.

1. 15-5. К определению движущей силы процесса массопереноса в

концентрациях . Ф,(а)иФ,(^)

При А^б/А^ < 2 движущая сила может определяться как сред-

неарифметическая, т.е. А>'ср = (Д^ + А>^)/2.

Аналогичные выражения будут и для прямоточного движения фаз,

участвующих в массообмене. Более общие зависимости для определения движущей

силы, когда линия равновесия криволинейна и структура потоков отлична от

идеального вытеснения, будут рассмотрены ниже (см. разд. 15.7.2).

5.4. Методы РАСЧЕТА МАССООБМЕННЫХ АППАРАТОВ

При проведении технологических расчетов массообменных annaJ ратов

определяют их диаметр (если аппараты цилиндрической формы) и высоту (или

длину). Диаметр или сечение аппарата отражают его производительность, а высота-

интенсивность протекающих в аппарате процессов. Часто после завершения расчета

размеров массообменных аппаратов возникает необходимость определения их

гидравлического сопротивления. Подход к такому расчету рассмотрен в гл. 6. В

последующих разделах будут приведены конкретные уравнения для расчета

гидравлического сопротивления этих аппаратов.

5.4.1 Расчет диаметра аппарата

Обычно диаметр или поперечное сечение S массообменного аппарата

определяют по уравнению расхода

где б-объемный расход сплошной фазы, м

/^; wq приведенная (или

фиктивная) скорость той же фазы, отнесенная к полному сечению аппарата, м/с.

Для аппаратов круглого поперечного сечения диаметром D, наиболее

распространенных в технике, предыдущее выражение (3.9) принимает вид

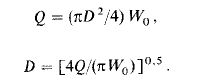
Значение Q обычно бывает задано или его сравнительно несложно

определить из уравнения материального или теплового

балансов.

Выбор скорости wq оказывается значительно сложнее, так как от величины

wq сильно зависит не только диаметр аппарата, но и его высота (так как величина wq

может существенно влиять на ^у и Р^), его гидравлическое сопротивление, а также

величина брызгоуноса. Если гидравлическое сопротивление не имеет большого

значения, то при выборе скорости нужно учитывать, что обычно выгоднее брать

скорость, близкую к предельной, ограничиваемой точкой захлебывания. Для

наиболее распространенных массообменных аппаратов уравнения (часто

эмпирические) для расчета скорости захлебывания известны (они для некоторых

аппаратов приведены