Идельчик В.И. Электрические системы и сети

Подождите немного. Документ загружается.

400 Расчеты режимов электрических

систем

и сетей на ЭВМ Гл. 9

системы (9.1) итерационный процесс метода Зейделя опи-

сывается следующим выражением:

I+1)

Ul°-\ Ь

1з

иР +h;

г/Г»

= ь

t/j«+

+ь,М

1+Х)

+ь

По методу простой итерации (t+l)-e приближение /г-го

напряжения

U%+

для системы /г-го порядка вычисляется

по следующему выражению:

</i

,+l,

-2*«<

sl+

2 **"/

(|,

* (

По методу Зейделя (г-f-1) -е приближение /г-ro напря-

жения

{/<,'+'>

вычисляется так:

,+1)

+ 2

*»

^°

**•

Можно показать, что метод Зейделя эквивалентен про-

стой итерации (9.37), но с другой матрицей и другим век-

тором

Как правило, метод Зейделя надежнее и быстрее схо-

дится, чем метод простой итерации Кроме того, метод Зей-

деля требует несколько меньшей пямяги, чем простая ите-

рация, так как необходимо помнить только один вектор

переменных. Действительно, при решении по Зейделю, напри-

мер,

уравнений узловых напряжений сразу после вычисле-

ния (t-l-l)-e приближение /г-го узлового напряжения t/['+

записывается в ту же ячейку памяти, где ранее хранилось

i-e приближение £/|

()

. При использовании простой итерации

необходимо помнить два вектора узловых напряжений, со-

ответствующих £-му и (t'-(-l)-My шагам.

Алгоритмическая реализация метода Зейделя столь же

проста, как и простой итерации. Единственное изменение

в алгоритме расчета состоит в засылке вычисленного £/<'+•>

в то же место памяти, где ранее хранилось

U%K

Поскольку метод простой итерации не имеет никаких

преимуществ перед методом Зейделя, при практических ра-

счетах установившихся режимов электрических систем на

§ 9.2

Методы решения линейных уравнений

узловых

напряжений

401

»' —- ——•

ЭВМ всегда используется метод Зейделя, а не простая ите-

рация.

Если метод Зейделя сходится быстро и для решения си-

стемы п-го порядка требуется менее п шагов, то при расче-

те на ЭВМ получим выигрыш во времени в сравнении сточ-

ными методами, например с методом Гаусса. Это вытекает

из того, что число арифметических операций, необходимых

для одного шага метода Зейделя, пропорционально п

, а об-

щее число арифметических операций, например в методе

Гаусса, пропорционально и

. Приведенное соотношение чис-

ла операций справедливо для расчетов установившегося

режима, если не учитывается слабая заполненность матриц

узловых проводимостей. В то же время и в случае учета

слабой заполненности этих матриц метод Зейделя, если он

сходится быстро, требует меньше времени ЭВМ, чем точ-

ные методы.

Важное достоинство метода Зейделя состоит в простоте

алгоритма и в удобстве его реализации на ЭВМ. Он осо-

бенно эффективен при учете слабой заполненности матрицы

узловых проводимостей, поскольку алгоритм такого учета

в методике Зейделя весьма прост. В результате экономия

памяти при использовании метода Зейделя становится тем

существенней, чем больше узлов содержит электрическая

система. Применение специальных методов учета слабой

заполненности при применении точных методов несколько

уменьшает преимущество метода Зейделя с точки зрения

необходимого объема памяти ЭВМ. Однако в точных мето-

дах такой учет алгоритмически сложен и даже при его при-

менении метод Зейделя все равно требует меньше памяти

ЭВМ. Вопросы экономии памяти играют важную роль при

сопоставлении различных методов расчета режимов и бо-

лее подробно рассмотрены в гл. 10.

Существенный недостаток метода Зейделя — его мед-

ленная сходимость или даже расходимость при расчете

электрических систем с устройствами продольной компен-

сации, с трехобмоточными трансформаторами, когда сопро-

•

ивление обмотки среднего напряжения очень мало, а так-

же при расчетах предельных и неустойчивых режимов.

М-237

402 Расчеты режимов электрических систем и сетей на ЭВМ Гл. 9

9.3. ПРИМЕРЫ РЕШЕНИЯ ЛИНЕЙНЫХ УРАВНЕНИЙ

УЗЛОВЫХ НАПРЯЖЕНИЙ

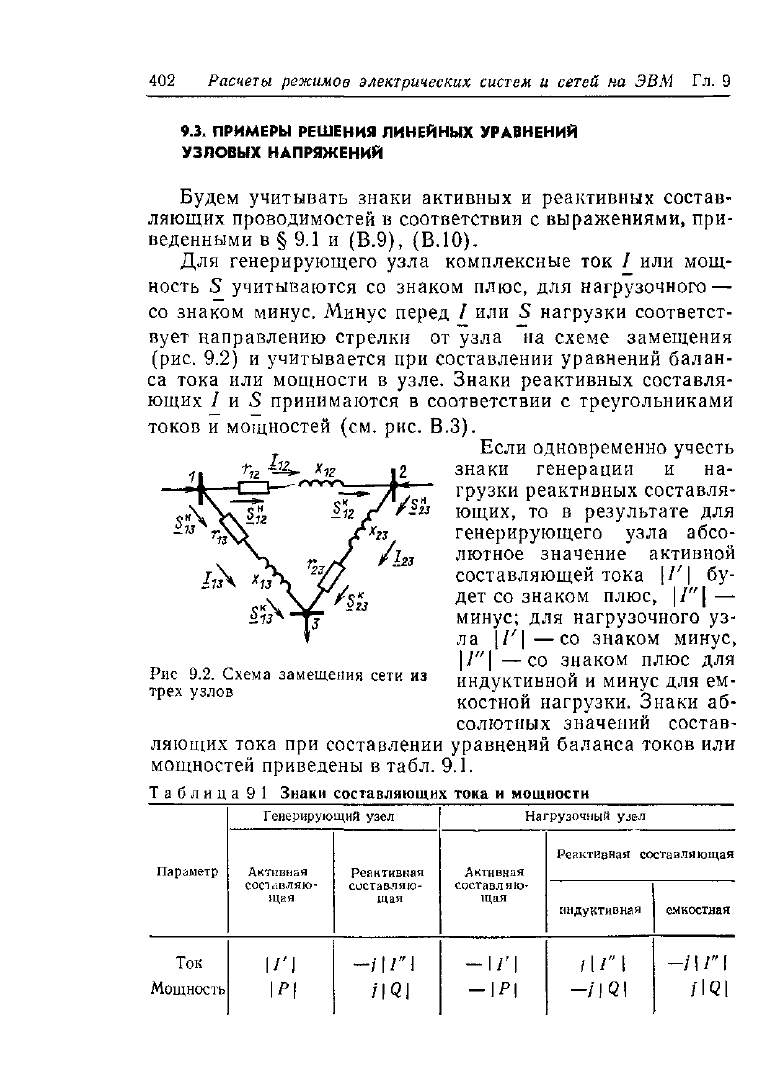
Будем учитывать знаки активных

реактивных состав-

ляющих проводимостей

соответствии

выражениями, при-

веденными

в §

9.1

(В.9), (В.10).

Для генерирующего узла комплексные

ток

или

мощ-

ность

учитываются

со

знаком плюс,

для

нагрузочного

—

со знаком минус. Минус перед

или

нагрузки соответст-

вует направлению стрелки

от

узла

на

схеме замещения

(рис.

9.2) и

учитывается при составлении уравнений балан-

са тока

или

мощности

узле. Знаки реактивных составля-

ющих

I и S

принимаются

соответствии

треугольниками

токов

мощностей (см. рис.

В.З).

Если одновременно учесть

знаки генерации

и на-

грузки реактивных составля-

ющих,

то в

результате

для

генерирующего узла абсо-

лютное значение активной

составляющей тока

|/'| бу-

дет

со

знаком плюс,

\1"\ —

минус;

для

нагрузочного

уз-

ла |/'|—со знаком минус,

|/"|

—со

знаком плюс

для

индуктивной

минус для

ем-

костной нагрузки. Знаки

аб-

солютных значений состав-

ляющих тока при составлении уравнений баланса токов

или

мощностей приведены

табл. 9.1.

Таблица 91 Знаки составляющих тока и мощности

Рис 9.2. Схема замещения сети из

трех узлов

Генерирующий узел Нагрузочный узел

Параметр Активная

составляю-

щая

Реактивная

составляю-

щая

Активная

составляю-

щая

Реактивная составляющая

Активная

составляю-

щая

Реактивная

составляю-

щая

Активная

составляю-

щая

ин

ДУКТивная

емкостная

Ток

Мощность

-/in

/IQI

-l/'l

-\Р\

-/IQI

/IQI

9.3

Примеры решения линейных уравнений

403

Пример

9.1.

Составим уравнения узловых напряжений

виде

(9 20)

и (9.21)

для

электрической сети, схема замещения которой приведена

на рис.

9.2.

В схеме

на рис.

9.2

—

три линии электропередачи,

два

генераторных

узла

1, 2 и

нагрузочный узел

Сопротивления линий следующие:

Z\i=

= 10+/20

Ом;

=15+/30

Ом;

=Ю+/25

Ом.

Узел

принят

каче-

стве балансирующего

базисного, напряжение t/i

£/б= 115

кВ

Зада-

ющие токи

узлах

2 и 3

соответственно равны

= /2+

Ц2

——(0,2624— /0,1575)

кА,

+,/

(—0,4199+ /0,2099)

кА.

Уз

Если определять трехфазные мощности

узлах

по

выражению

}/~3U

H0M

[

TOS

28,8675+ /17,3205

МВ-А;

=—46,1880 —/23,0940

МВ-А.

По заданным сопротивлениям ветвей вычисляем

их

проводимости,

Ом-',

по

формулам

2), (9.3):

=—\./Z

; Y

=—2Y

; У

= — (У|3+

^2з);

^33 =— (^13+

Уш)',

Ги

в»

/*и

°'

+/°'

;

Ъ»

=«i,

-Ibis =-0,0133

/0,0267;

У и

= £

з -

1Ь„

0,0138

/0,0345;

£,»

= £» - /6» =

0,0338

/0,0745;

Yjn

8г>з

— Ai =

0.0271 — /0,0612.

Матрица

для

трехузловой сети'

Для схемы

на рис. 9.2

матрица проводимостей

0,0338 —0,0138

—0,0138 0,0271

—

0,0745 —0,0345

—0,0345 0,0612

Вектор задающих токов

для

данной схемы

h h

0,2624

—0,4199

Уз

—0,1575

0,2099

404 Расчеты режимов электрических систем и сетей на ЭВМ Гл. 9

Вектор узловых напряжений

"г

Вектор YeUa для данной схемы с учетом задания напряжения

в базисном узле Ue= 115 кВ

(0,02—/0,04)-115

(gal— i

n)V6

tesi —/631)^6

(0,0133—

/0,0267)-115

Запишем систему узловых напряжений в виде (9.21):

#22 #23*22*23

#32 #33 32 33

#22 #23

32 33 #23 #33

и'

-Уз

#21

#31^6

.(9.41)

Если подставить значения активных и реактивных составляющих

проводимостей, узловых токов и базисного напряжения, то получим

в матричном виде

0, ,0338 —0,0138 0,0745 —0,0345

—0,0138 0,0271 —0,0345 0,0612

—0,0745 0,0345 0,0338 —0,0138

0,0345 —0,0612 —0,0138 0,0271

^з

Уз

0,2624

—0,4199

—0,1575

0,2099

0,02-115

0,0133-115

—0,04-115

—0,0267-115

или в виде системы уравнений

0,0338 ^з

—

0,0138^3 + 0,0745[/'з — 0,0345^3 = 2,5624;

—0,0138^2 + 0,027Ш

— 0,0345С/'2 + 0,0612£/'з = 1, Ю96;

—0,0745^

+ 0,0345С/з + 0,0338^2 — 0,0138У3 =—4,7575;

0,0345(72 —0,0612(;з —0,0138^2 + 0,0271^3=—2,8606.

Пример 9.2. Запишем систему уравнений установившегося режима

(9.42)

§ 9.3 Примеры решения линейных уравнений 405

из примера 9.1, сформировав матрицу коэффициентов следующим об-

разом:

—By

Определим напряжения в узлах, решив записанную систему по ме-

тоду Гаусса

Такое формирование матрицы удобно с точки зрения решения по-

лученных уравнений итерационными методами, сходимость которых улуч-

шается, если диагональные элементы доминируют, т. е. по абсолютной

величине больше всех остальных элементов в строке

В этом случае уравнение (9 21) запишется в виде

= 1/з

|Г

—

—bft6 U'б

(9.43)

(9.44)

Система уравнений (9 42) примет вид

0,0745i/2 —0,0345^3+0,0338(72 —0,0138^3 = 2,5624;

—0,0345^2 + 0,0612(/з — 0,0138^2 + 0,0271 и'

1,1096,

0,0338^2 — 0,0138Уз— 0,0745^2 + 0,0345(;з=— 4,7575;

—

0,0138(/2 + 0,027Шз +0,0345t/2 — 0,0612^3 = — 2,8606.

После исключения U

получим систему уравнений

—0,463Шз+ 0,4537(/2 — 0,1852(;з = 34,3946;

0,0452Уз + 0,00190, + 0,0207У

= 2,2962;

0,0019С/

—

0,0898^2 + 0,0408^3 =— 5,920;

0,0207 и"

+ 0,0408(/2 — 0,0638^3 =—2,3860.

Далее исключим £/

U\ — 0,4631 и"

+ 0,4537^2

—

0,1852и'

= 34,3946;

и"

0,0420U'

+ 0,4580Уз = 50,8009;

— 0,0899С/

+ 0,0399

=—

6,0165;

0,0399(/

— 0,0733^3 =— 3,4376.

Затем исключим U

и систему уравнений (9.44) приведем к экви-

Нлентиой системе с треугольной матрицей.

406 Расчеты режимов электрических систем и сетей на ЭВМ Гл. 9

— 0,463Шз + 0,4537(72 —0,1852(4 = 34,3946;

и'з + 0,0420(72 + 0,4580(/з= 50,8009;

(72

—

0,4438(73 = 66,9244;

—

0,0556(/з=— 6,1078.

Из этой системы последовательно найдем значения неизвестных:

= 115,6777 кВ; (7j= 109,8543 кВ;

= 0,2325 кВ; (7д =— 4,3708 кВ.

При решении системы (9.44) с точностью до семи значащих десятич-

ных цифр получены следующие значения напряжений, которые различа-

ются с приведенными выше на величину погрешности округления:

= 115,7188 кВ; и'

= 109,9964 кВ;

(72 = 0,2612 кВ; и"

=— 4,3362 кВ.

Пример 9.3. Определить напряжения узлов для схемы иа рис. 9.2

по данным примера 9.1 методом обратной матрицы.

Активные и реактивные составляющие узловых напряжений будем

определять аналогично примеру 9.2 из выражения, которое следует из

,(9.43):

и;

+ Кз

°у

-1

°у

_в

(9.45)

где U

и U

— векторы, каждый элемент которых равен (7

или (7

т, е. активной или реактивной составляющей Ua.

Можно показать, что система (9.45) эквивалентна (9.43) [19]. Об-

ратную матрицу вычислим с помощью метода, основанного иа после-

довательной перестановке элементов столбцов неизвестных и правых час-

тей в системе линейных алгебраических уравнений [19].

Будем использовать, как и в примере 9.2, матрицу коэффициентов

в системе (9.44). Обратная матрица

-В,

14,6714 7,9953 7,1491 4,2623

7,9953 18,0109 4,2623

8,5753

7,1491 4,2623 —14,6714 — 7,9953

4,2623

8,5753

—7,9953 —18,0109

Составляющие напряжений узлов

§ 9.3 Примеры решения линейных уравнений 407

115

14,6714 7,9953 7,1491 4,2623 0,2624

7,9953 18,0109 4,2623

8,5753

—0,4199

7,1491 4,2623 —14,6714 —7,9953 ' —0,1575

4,2623

8,575

—7,9953 —18,0109 0,2099

0,2612

—4,3362

115,7187

109,9964

Таким образом, U

=115,7187 кВ; U

=0,2612 кВ, t/

=109,9964;

£/

=—4,3362 кВ, т. е. полученные значения напряжений различаются

с результатами примера 9 2 на величину погрешности округления.

Пример 9.4. Определим напряжения в узлах, решая методом прос-

той итерации уравнения узловых напряжений для сети, схема замеще-

ния которой приведена на рис. 9.2 и используя данные примера 9.1.

Систему уравнений (9.42) будем использовать в виде (9.44) и при-

ведем к виду, удобному для применения метода простой итерации:

= —0,4631£/

—0,4537L/

+0,1852t/

+34,3946

С/з = 0,56371/2 +0,2255(/2 — 0,4428L/3 +18,1307

0,4537U"

—0,1852(Уз + 0,463 W'

+63,8591

=—0,2255L/

+0,44281/з +0,5&37U

+46,7418

Принимаем начальные приближения действительных и мнимых

ставляющих узловых напряжений

46)

со-

и;м

ф)

7/'(0)

по

;/<0>

по

Определим первое приближение:

408 Расчеты режимов электрических систем и сетей на ЭВМ Гл. 9

0 0,4631 —0,4537 0,1852

0,5637 0 0,2255 —0,4428

0,4537 —0,1852 О

—0,2255 0,4428 0,5637

0,4631

34,3946

0 18,1307

по +

63,8591

по

46,7418

Полученные новые значения узловых напряжений подставляем

в правую часть (9.46) и т. д.

Дальнейший расчет произведен на ЭВМ. Результаты расчета ите-

рационного процесса при заданной точности по напряжениям е=

= 10-

£/ном =

0,001

кВ приведены в табл. 9.2.

Таблица 9 2. Результаты расчета на ЭВМ методом простой итерации

Номер

г.терации

, кВ

. кВ

, кВ

i/з. кв

'46

4,8644

0,2618

0,2608

0,2611

-5,7745

—4,3369

-4,3358

—4,3361

ПО

114,7987

115,7188

115,7191

115,7183

ПО

108,7516

109,9963

109,9960

109,9969

Результаты расчета совпадают с результатами примеров 9.2 и 9.3

с точностью до погрешности округления.

Пример 9.5. Определим напряжения в узлах, решив методом Зей-

деля уравнения узловых напряжений для сети, схема замещения кото-

рой приведена на рис. 9 2, и используя данные примера 9.1.

Систему уравнений (9.42) будем использовать в виде (9.46), удоб-

ном для применения метода простой итерации.

Принимаем начальные приближения узловых напряжений

У*<°»

//'(О)

7/(0)

ПО

"з

по

Первое приближение £/

определим из первого уравнения системы

§ 9.3 Примеры решения линейных уравнений 409

(9.46):

t/'W =0-0+ 0,4631-0 —0,4537.110 + 0,1852-110 +

+ 34,3946 = 4,8596.

Подставим {Л,'

', U

^, сУ

<0)

. ^з

(

°'

во

второе уравнение системы

(9.46):

=0,5637-4,8596+ 0-0+ 0,2255-ПО—0,4428-110 +

+ 18,1307=—3,0329.

Аналогично подставим в третье уравнение U

, U^ ', С/

<0)

, У

(

получим

{1)

=0,4537-4,8596

—

0,1852-3,0329 + 0-110 +

0,4631

X 110 + 63,8591 = 117,5666.

И, наконец, подставив u"

L/'^

(1)

в последнее урав-

нение, определим

Уз

(1)

=—0,2255-4,8596+ 0,4428-3,0329+ 0,5637-117,5666 +

+ 0-110 + 46,7418= 110,5753.

Дальнейший расчет произведен на ЭВМ. Результаты расчета при за-

данной точности по напряжениям е=10

-5

1Уном=0,001 кВ приведены

в табл. 9.3.

Таблица 9.3. Результаты расчета на ЭВМ методом Зеиделя

Номер

итерации

, кВ

ul KB

U%,

кВ

и'з,

кВ

4,8644

0,2616

0,2614

—3,0323

—4,3360

—4,3361

ПО

117,5673

115,7185

115,7187

ПО

110,5779

109,9962

109,9964

Результаты расчетов совпадают с результатами примеров 9.2 —9.4

с точностью до погрешности округления. Из табл. 9.2

—

9.3 видно, что

метод Зеиделя сходится значительно быстрее, чем метод простой ите-

рации.