Hull J.C. Risk management and Financial institutions

Подождите немного. Документ загружается.

Chapter 4

so that the bond price goes down to 94.213 — 0.250 = 93.963. How accurate is

this? When the bond yield increases by 10 basis points to 12.1%, the bond

price is

which is (to three decimal places) the same as that predicted by the duration

relationship.

Modified Duration

The preceding analysis is based on the assumption that y is expressed with

continuous compounding. If y is expressed with annual compounding, it

can be shown that the approximate relationship in equation (4.11)

becomes

More generally, if y is expressed with a compounding frequency of m

times per year, then

A variable D* defined by

is sometimes referred to as the bond's modified duration. It allows the

duration relationship to be simplified to

when y is expressed with a compounding frequency of m times per year.

The following example investigates the accuracy of the modified duration

relationship.

Example 4.6

The bond in Table 4.5 has a price of 94.213 and a duration of 2.653. The yield,

expressed with semiannual compounding is 12.3673%. The modified duration

From equation (4.13), we have

Interest Rate Risk

When the yield (semiannually compounded) increases by 10 basis points

(=0.1%), =+0.001. The duration relationship predicts that we expect

to be —235.39 x 0.001 = —0.235, so that the bond price goes down to

94.213 - 0.235 = 93.978. How accurate is this? When the bond yield (semi-

annually compounded) increases by 10 basis points to 12.4673% (or to

12.0941% with continuous compounding), an exact calculation similar to that

in the previous example shows that the bond price becomes 93.978. This shows

that the modified duration calculation is accurate for small yield changes.

4.6 CONVEXITY

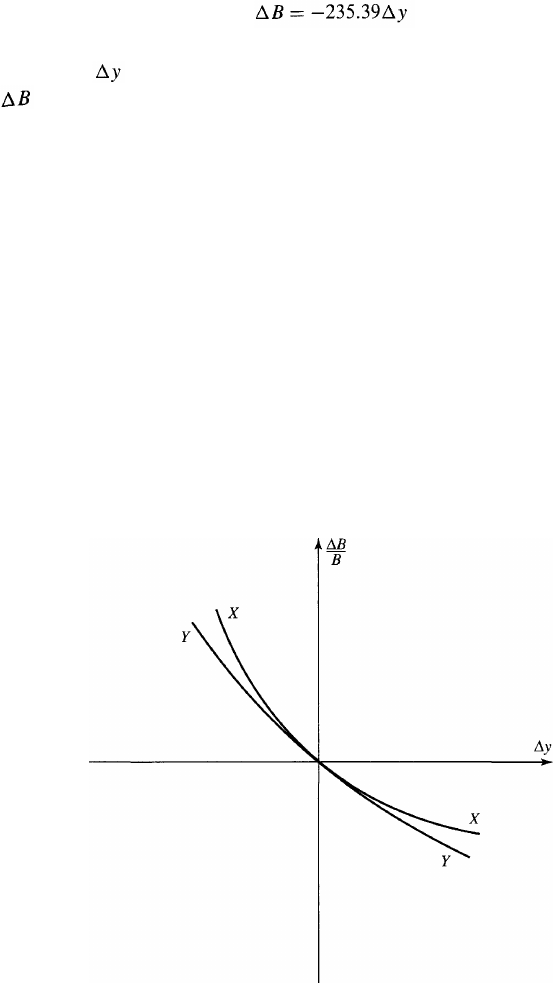
The duration relationship measures exposure to small changes in yields.

This is illustrated in Figure 4.2, which shows the relationship between the

percentage change in value and change in yield for bonds having the same

duration. The gradients of the two curves are the same at the origin. This

means that both portfolios change in value by the same percentage for

small yield changes, as predicted by equation (4.12). For large yield

Figure 4.2 Two portfolios with the same duration.

94 Chapter 4

changes, the portfolios behave differently. Portfolio X has more curvature

in its relationship with yields than Portfolio Y. A factor known as

convexity measures this curvature and can be used to improve the

relationship in equation (4.12).

A measure of convexity for a bond is

where y is the bond's yield. This is the weighted average of the square of

the time to the receipt of cash flows. From Taylor series expansions, a

more accurate expression than equation (4.9) is

This leads to

Example 4.7

Consider again the bond in Table 4.5: the bond price B is 94.213 and the

duration D is 2.653. The convexity is

0.05 x 0.5

+ 0.047 x 1.0

+ 0.044 x 1.5

+ 0.042 x 2.0

+ 0.039 x 2.5

+ 0.779 x 3.0

= 7.570

The convexity relationship in equation (4.14) is therefore

Consider a 2% change in the bond yield from 12% to 14%. The duration

relationship predicts that the dollar change in the value of the bond will be

—94.213 x 2.653 x 0.02 = —4.999. The convexity relationship predicts that it

will be

-94.213 x 2.653 x 0.02 + 0.5 x 94.213 x 7.570 x 0.02

= -4.856

The actual change in the value of the bond is —4.859. This shows that the

convexity relationship gives much more accurate results than duration for a

large change in the bond yield.

4.7 APPLICATION TO PORTFOLIOS

The duration concept can be used for any portfolio of assets dependent

on interest rates. Suppose that P is the value of the portfolio. We make a

Interest Rate Risk

small parallel shift in the zero-coupon yield curve and observe the change

in P. Duration is defined as

where is size of the parallel shift. Equation (4.12) becomes

Suppose the portfolio consists of a number of assets. The ith asset is

worth X

and has a duration D

(i = 1,..., n). Define as the change

in the value of X

arising from the yield curve shift It follows that

so that the duration of the portfolio is

given by

The duration of the ith asset is

Hence,

This shows that the duration D of a portfolio is the weighted average of

the durations of the individual assets comprising the portfolio with the

weight assigned to an asset being proportional to the value of the asset.

The convexity can be generalized in the same way as the duration. For

an interest-rate-dependent portfolio with value P, we define the convexity

as 1/P times the second partial derivative of the value of the portfolio

with respect to a parallel shift in the zero-coupon yield curve. Equation

(4.14) is correct with B replaced by P:

(4.16)

The relationship between the convexity of a portfolio and the convexity of

the assets comprising the portfolio is similar to that for duration: the

convexity of the portfolio is the weighted average of the convexities of the

assets with the weights being proportional to the value of the assets.

96 Chapter 4

The convexity of a bond portfolio tends to be greatest when the

portfolio provides payments evenly over a long period of time. It is least

when the payments are concentrated around one particular point in time.

Portfolio Immunization

A portfolio consisting of long and short positions in interest-rate-

dependent assets can be protected against relatively small parallel shifts

in the yield curve by ensuring that its duration is zero. It can be

protected against relatively large parallel shifts in the yield curve by

ensuring that its duration and convexity are both zero or close to zero.

In this respect duration and convexity are analogous to the delta and

gamma Greek letters we encountered in Chapter 3.

4.8 NONPARALLEL YIELD CURVE SHIFTS

Unfortunately, the basic duration relationship in equation (4.15) only

quantifies exposure to parallel yield curve shifts. The duration plus

convexity relationship in equation (4.16) allows the shift to be relatively

large, but it is still a parallel shift.

Some researchers have attempted to extend duration measures so that

nonparallel shifts can be considered. Reitano suggests a partial duration

measure where just one point on the zero-coupon yield curve is shifted

and all other points remain the same.

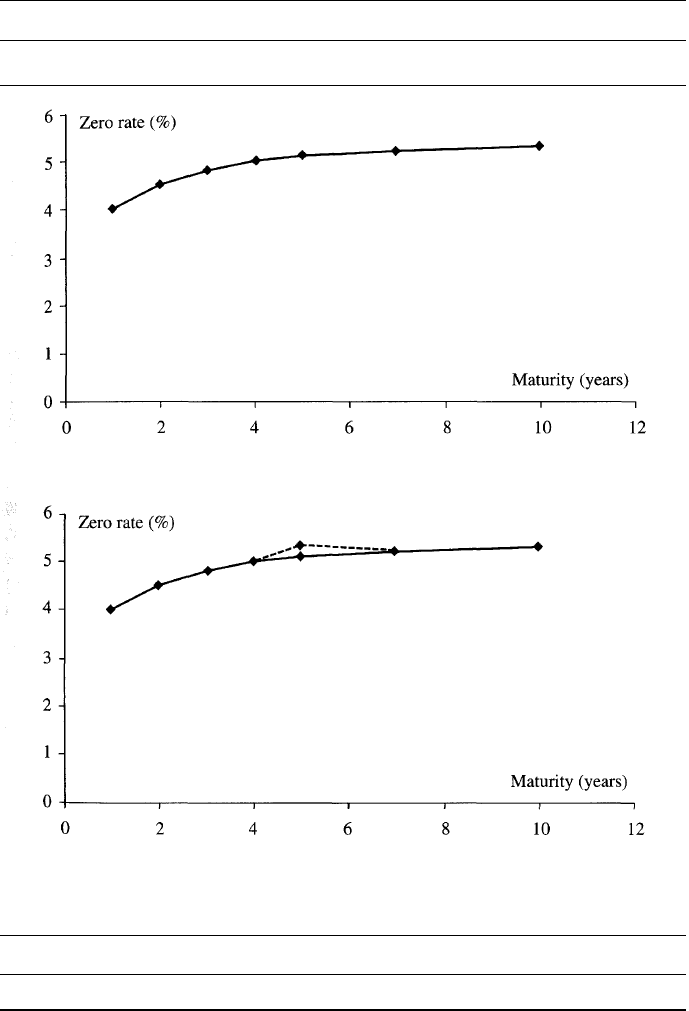
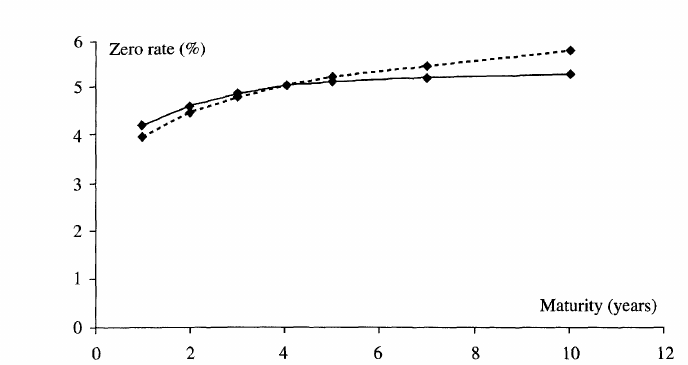
Suppose that the zero curve is as

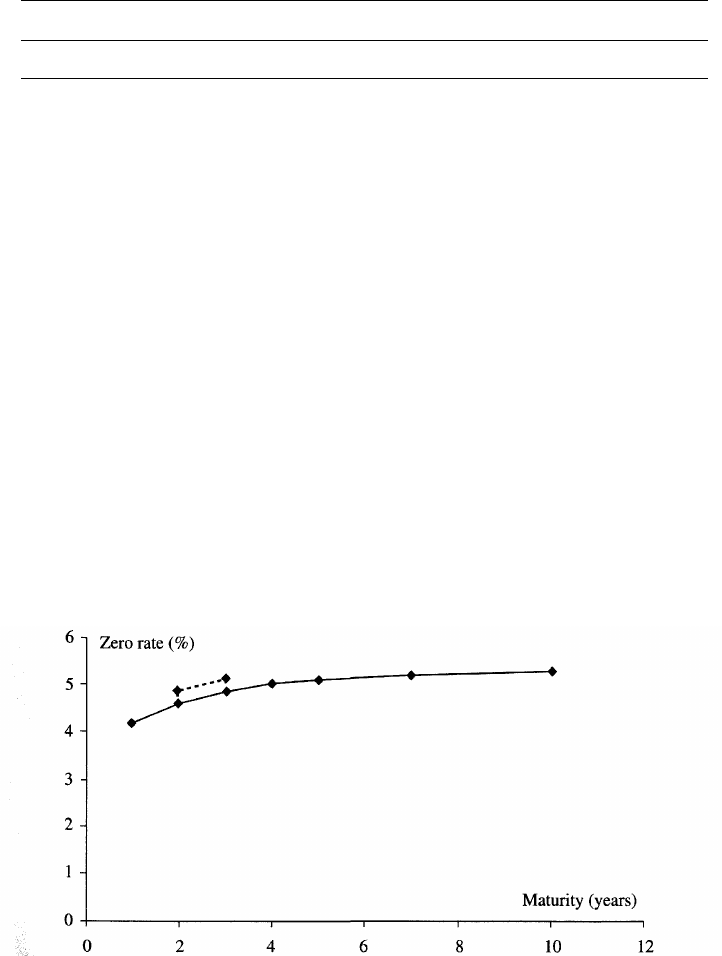
shown in Table 4.6 and Figure 4.3. Shifting the five-year point involves

changing the zero curve as indicated in Figure 4.4. In general, the partial

duration of the portfolio for the ith point on the zero curve is

where is the size of the small change made to the ith point on the yield

curve and is the resultant change in the portfolio value. The sum of

all the partial duration measures equals the usual duration measure.

Suppose that the partial durations for a particular portfolio are as

shown in Table 4.7. The total duration of the portfolio is only 0.2. This

means that the portfolio is relatively insensitive to parallel shifts in the

yield curve. However, the durations for short maturities are positive while

See R. Reitano, "Non-Parallel Yield Curve Shifts and Immunization," Journal of

Portfolio Management, Spring 1992, 36-43.

Interest Rate Risk 97

Table 4.6 Zero-coupon yield curve (rates continuously compounded).

Maturity (years)

Rate (%)

4.0

4.5

4.8

5.0

5.1

5.2

5.3

Figure 4.3 The zero-coupon yield curve in Table 4.6.

Figure 4.4 Change in zero-coupon yield curve when one point is shifted.

Table 4.7 Partial durations for a portfolio.

Maturity (years)

Duration

2.0

1.6

0.6

0.2

-0.5

-1.8

-1.9

Total

0.2

98 Chapter 4

Figure 4.5 A rotation of the yield curve.

those for long maturities are negative. This means that the portfolio loses

(gains) in value when short rates rise (fall). It gains (loses) in value when

long rates rise (fall).

We are now in a position to go one step further and calculate the

impact of nonparallel shifts. We can define any type of shift we want.

Suppose that, in the case of the yield curve shown in Figure 4.3, we define

a rotation where the changes to the 1-year, 2-year, 3-year, 4-year, 5-year,

7-year, and 10-year points are — 3e, —2e, —e, 0, e, 3e, and 6e for some

small e. This is illustrated in Figure 4.5. From the partial durations in

Table 4.7, the percentage change in the value of the portfolio arising from

the rotation is

2.0 x (-3e) + 1.6 x (-2e) + 0.6 x (-e) + 0.2 x 0

- 0.5 x e - 1.8 x 3e - 1.9 x 6e = -27.1e

This shows that a portfolio that gives rise to the partial durations in Table

4.7 is much more heavily exposed to a rotation of the yield curve than to a

parallel shift.

4.9 INTEREST RATE DELTAS

We now move on to consider how the Greek letters discussed in Chapter 3

can be calculated for interest rates. One possibility is to define the delta of

a portfolio as the change in value for a one-basis-point parallel shift in

the zero curve. This is sometimes termed a DV01. It is the same as the

Interest Rate Risk 99

Table 4.8 Deltas for portfolio in Table 4.7. Value of Portfolio is $1 million.

The dollar impact of a one-basis-point shift in points on the zero curve is shown.

Maturity (years)

Delta

200

160

-50

-180

-190

Total

duration of the portfolio multiplied by the value of the portfolio multi-

plied by 0.0001.

In practice, analysts like to calculate several deltas to reflect their

exposures to all the different ways in which the yield curve can move.

There are a number of different ways this can be done. One approach

corresponds to the partial duration approach that we outlined in the

previous section. It involves computing the impact of a one-basis-point

change similar to the one illustrated in Figure 4.4 for each point on the

zero-coupon yield curve. This delta is the partial duration calculated in

Table 4.7 multiplied by the value of the portfolio multiplied by 0.0001.

The sum of the deltas for all the points on the yield curve equals the

DV01. Suppose that the portfolio in Table 4.7 is worth $1 million. The

deltas are shown in Table 4.8.

A variation on this approach is to divide the yield curve into a number

of segments or "buckets" and calculate for each bucket the impact of

changing all the zero rates corresponding to the bucket by one basis

point while keeping all other zero rates unchanged. This approach is

often used in asset-liability management (see Section 1.5) and is referred

to as GAP management. Figure 4.6 shows the type of change that would

Figure 4.6 Change considered to yield curve when bucketing approach is used.

100

Chapter 4

be considered for the segment of the zero curve between 2.0 and 3.0 years

in Figure 4.3. Again, the sum of the deltas for all the segments equals

the DV01.

Calculating Deltas to Facilitate Hedging

One of the problems with the delta measures that we have considered so

far is that they are not designed to make hedging easy. Consider the deltas

in Table 4.8. If we plan to hedge our portfolio with zero-coupon bonds,

we can calculate the position in a one-year zero-coupon bond to zero out

the $200 per basis point exposure to the one-year rate, the position in a

two-year zero-coupon bond to zero out the exposure to the two-year rate,

and so on. But, if other instruments are used, a much more complicated

analysis is necessary.

In practice, traders tend to use positions in the instruments that have

been used to construct the zero curve to hedge their exposure. For

example, a government bond trader is likely to take positions in the

actively traded government bonds that were used to construct the Treas-

ury zero curve when hedging. A trader of instruments dependent on the

LIBOR/swap yield curve is likely to take positions in LIBOR deposits,

Eurodollar futures, and swaps when hedging.

To facilitate hedging, traders therefore often calculate the impact of

small changes in the quotes for each of the instruments used to construct

the zero curve. Consider a trader responsible for interest rate caps and

swap options. Suppose that the trader's exposure to a one-basis-point

change in a Eurodollar futures quote is $500. Each Eurodollar futures

contract changes in value by $25 for a one-basis-point change in the

Eurodollar futures quote. It follows that the trader's exposure can be

hedged with 20 contracts. Suppose that the exposure to a one-basis-point

change in the five-year swap rate is $4,000 and that a five-year swap with a

notional principal of $ 1 million changes in value by $400 for a one-basis-

point change in the five-year swap rate. The exposure can be hedged by

trading swaps with a notional principal of $10 million.

4.10 PRINCIPAL COMPONENTS ANALYSIS

The approaches we have just outlined can lead to analysts calculating

10 to 15 different deltas for every zero curve. This seems like overkill

because the variables being considered are quite highly correlated with

each other. For example, when the yield on a five-year bond moves up by

Interest Rate Risk

101

Table 4.9 Factor loadings for US Treasury data.

12m

10y

30y

PC1

0.21

0.26

0.32

0.35

0.36

0.34

0.31

0.25

PC2

-0.57

-0.49

-0.32

-0.10

0.02

0.14

0.17

0.27

0.30

0.33

PC3

0.50

0.23

-0.37

-0.38

-0.30

-0.12

-0.04

0.15

0.28

0.46

PC4

0.47

-0.37

-0.58

0.17

0.27

0.25

0.14

0.01

-0.10

-0.34

PC5

-0.39

0.70

-0.52

0.04

0.07

0.16

0.08

0.00

-0.06

-0.18

PC6

-0.02

0.01

-0.23

0.59

0.24

-0.63

-0.10

-0.12

0.01

0.33

PC7

0.01

-0.04

0.56

-0.79

0.15

0.09

0.13

0.03

-0.09

PC8

0.00

-0.02

-0.05

0.12

0.00

0.55

-0.26

-0.54

-0.23

0.52

PC9

0.01

-0.01

0.00

-0.12

-0.09

-0.14

0.71

0.00

-0.63

0.26

PC10

0.00

0.01

-0.05

-0.00

-0.08

0.48

-0.68

0.52

-0.13

a few basis points, most of the time the yield on a ten-year bond does the

same. Arguably a trader should not be worried when a portfolio has a

large positive exposure to the five-year rate and a similar large negative

exposure to the ten-year rate.

One approach to handling the risk arising from groups of highly

correlated market variables is principal components analysis. This takes

historical data on movements in the market variables and attempts to

define a set of components or factors that explain the movements.

The approach is best illustrated with an example. The market variables

we will consider are ten US Treasury rates with maturities between three

months and 30 years. Tables 4.9 and 4.10 show results produced by Frye

for these market variables using 1,543 daily observations between 1989

and 1995.

The first column in Table 4.9 shows the maturities of the rates

that were considered. The remaining ten columns in the table show the

ten factors (or principal components) describing the rate moves. The first

factor, shown in the column labeled PC1, corresponds to a roughly

parallel shift in the yield curve. When we have one unit of that factor,

Table 4.10 Standard deviation of factor scores (basis points).

See J. Frye, "Principals of Risk: Finding VAR through Factor-Based Interest Rate

Scenarios." In VAR: Understanding and Applying Value at Risk, Risk Publications,

London, 1997, pp. 275-288.

PCI

17.49

PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9

6.05 3.10 2.17 1.97 1.69 1.27 1.24 0.80

PC10

0.79