Hooke R.L. Principles of glacier mechanics

Подождите немного. Документ загружается.

The steady-state temperature proﬁle 121

is θ

. (Note that in this case, rather than solve Equation (6.19)asan

indeﬁnite integral and then evaluate a constant of integration by applying

a boundary condition, it is more convenient to express the integrals as

deﬁnite integrals. Thus the boundary condition, θ = θ

on z = H,is

incorporated into the limits of integration. Further discussion of this

boundary condition is deferred for the moment.)

The integral on the right-hand side of Equation (6.20) does not have

a solution in closed form. However, it occurs frequently, and thus has

been tabulated. In addition, many computer statistical packages have

solutions. The challenge is to express it in the terms used in these tables.

We ﬁrst express the integral on the right-hand side as the difference

between integrals over the range 0 → H and 0 → h, thus:

− θ (h) = β







−ζ

dz −



−ζ





(6.21)

and then make the substitution: ζ z = t,whence dz = dt/ζ , and t = ζ h

on z = h.Wealso multiply and divide by

√

π/2, thus:

− θ (h) =

√





√

ζ H



−t

dt −

√

ζ h



−t





(6.22)

By deﬁnition:

erf (x ) =

√



−t

dt (6.23a)

where erf (x)iscalled the error function of x. Thus, our ﬁnal solution for

the temperature, θ(h), at depth h is:

θ(h) = θ

−

√

[

erf (ζ H ) − erf (ζ h)

]

(6.24)

As noted, erf (x) has been tabulated, so values of it can be looked

up, much as can values of a sine or cosine. Caution is required, how-

ever, as some tables deﬁne erf (x) slightly differently than we have in

Equation (6.23a), and thus require a different set of substitutions in

Equation (6.21). A common alternative deﬁnition is:

erf (x ) =

√

2π



−

dt (6.23b)

122 Temperature distribution in polar ice sheets

1.5

1.0

1234 5

erf

(x)

Figure 6.5. Values of the

error function, erf (x), as

deﬁned by Equation (6.23c),

and of Dawson’s integral, E(x),

for a typical range of values

of x = ζH. (Modiﬁed from

Budd, 1969, Figure 4.10.

Reproduced with permission

of the Australian Antarctic

Division.)

which requires the substitution: ζ z = t/

√

2. This leads to other changes

in Equations (6.22) and (6.24). Budd (1969) uses a less common deﬁni-

tion, namely:

erf (x ) =



−t

dt (6.23c)

and has plotted this (Figure 6.5) along with another function that arises

in calculations of temperature distributions in ice sheets. With this deﬁ-

nition, Equation (6.22) can be written:

θ(h) = θ

−

[

erf (ζ H ) − erf (ζ h)

]

(6.25)

In applying Equation (6.24)or(6.25), note that β

is negative in the

coordinate system of Figure 6.4.

The boundary condition at the surface

As noted, the boundary condition at the surface, z = H,isthe ice tem-

perature, θ

, and this must be known in order to calculate a temperature

proﬁle from Equations (6.24)or(6.25). Below, we will show that the

temperature at a depth of about 10 m in a glacier is very close to the

mean annual atmospheric temperature, θ

,soitisnormally assumed

that θ

= θ

.However, it may be well to note some situations in which

this approximation is not very good.

Temperatures in the ablation zones of some glaciers may be some-

what warmer than the mean annual temperature. This is because snow

insulates the ice during the winter, preventing cooling. In addition, per-

colating meltwater reaches the snow/ice interface soon after melting

starts in the spring, thus warming the ice faster than would be the case

with conduction alone. On Barnes Ice Cap, these two effects result in

The steady-state temperature proﬁle 123

near-surface ice temperatures that are about 2

◦

C above the mean annual

temperature (Hooke et al., 1983).

Somewhat higher on a glacier, near and above the equilibrium line,

percolating meltwater can penetrate into the ﬁrn of prior years. When

this water refreezes the heat of fusion is released at a signiﬁcant depth

in the glacier, not just at the snow/ice interface. The warming effect is

thus much enhanced, and ice temperatures in this zone may be several

degrees warmer than the mean annual temperature.

At high latitudes and altitudes on polar ice sheets, the ice temperature

may be slightly below the mean annual temperature because radiative

cooling during the clear winter night is more effective than heating during

the summer day.

Further discussion of these effects and additional references may be

found in Hooke et al.(1983).

Melting and freezing at the bed

In our analysis so far, we have tacitly assumed that the temperature at the

base of the glacier is below the melting point. However, this assumption

has not been incorporated into Equation (6.24)or(6.25). To be speciﬁc,

if the bed is at the pressure melting point and melting is occurring there,

some of the geothermal heat is clearly being used for that purpose and

is not being conducted upward into the ice. Thus, our estimate of β

likely to be too high. If we inadvertently insert such a value of β

into

Equation (6.24)or(6.25), the calculated temperature at the bed, θ

, will

turn out to be greater than the pressure melting temperature which is

clearly impossible.

To obtain a correct solution for the temperature proﬁle in this case, β

must be adjusted downward. The procedure is straightforward. Because

erf (0) = 0 and θ (0) = θ

pmp

, then at the pressure melting point temper-

ature, Equation (6.24) can be solved for β

, thus:

2ζ

√

(θ

− θ

pmp

)

erf (ζ H )

(6.26)

The melting point is depressed approximately 0.098 K MPa

−1

(if the

water produced is saturated with air) so, for example, θ

pmp

under 500 m

of ice would be ∼−0.4

◦

C. Inserting the value of β

obtained from

Equation (6.26) into Equation (6.24) and solving for temperatures at

other depths in the glacier will give the desired temperature proﬁle.

(Note that this approach is equivalent to solving Equation (6.17) with a

temperature boundary condition at the bed.)

The basal melt rate, dm/dt, can also be calculated. The heat available

for melting is the difference between the geothermal heat ﬂux and the

124 Temperature distribution in polar ice sheets

heat ﬂux into the ice, or K (β

− β

), where β

is the gradient that

would be required to conduct the geothermal ﬂux upward into the ice.

Thus, we obtain:

= K

(β

− β

)

∼

220(β

− β

)mma

−1

(6.27)

where L is the latent heat of fusion, and the result is in mm a

−1

if the

gradients are in K m

−1

It is also possible that water formed by basal melting at some dis-

tant locality has moved along the bed to the site at which the tempera-

ture proﬁle is to be calculated. Until all such water is refrozen, perhaps

incorporating sediment into the ice in the process, it will keep the basal

temperature at the pressure melting point. Again, Equation (6.24) does

not know about this water, so the intelligent scientist must intervene.

Presumably, he or she has calculated basal melt and freeze rates further

upglacier, and has kept track of how much of the water produced has not

refrozen. In any case, the procedure is similar to that above, except that

now the value of β

calculated from Equation (6.26) will be greater than

that necessary to conduct the geothermal heat upward into the ice, and

dm/dt in Equation (6.27) will be negative, indicating freezing.

Character of the temperature proﬁle

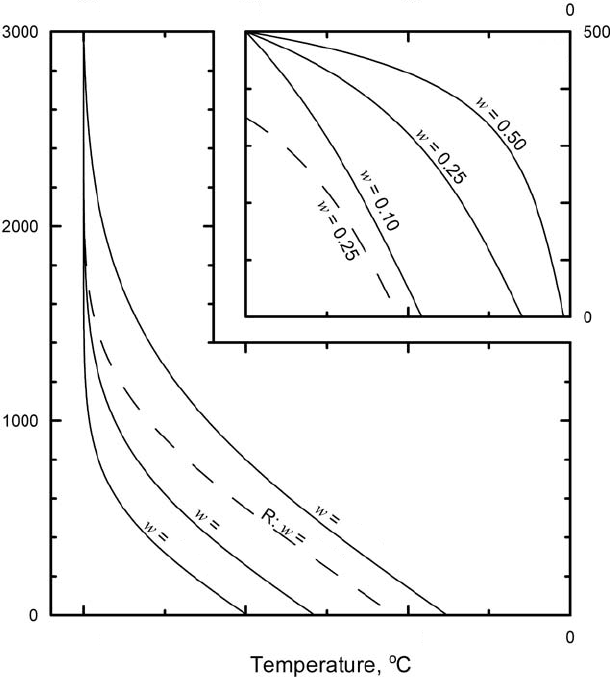
Several temperature proﬁles calculated from Equation (6.24) are shown

in Figure 6.6a.For the conditions assumed, the ice is nearly isothermal

in the upper few hundred meters and then warms rapidly near the bed.

Higher vertical velocities, resulting from higher accumulation rates at

the surface, increase the thickness of the isothermal zone and decrease

the basal temperature.

In essence, cold ice is advected downward from the surface, and

the upward-moving geothermal heat warms this descending ice. With

higher rates of advection (higher vertical velocities), the heat supplied

can warm a smaller fraction of the descending ice, so the ice column as

awhole is colder.

The shape of the temperature proﬁle can be understood qualitatively

in the following way. Consider the three elements of ice labeled A, B,

and C in Figure 6.7. All three are moving downward, but because w

decreases with depth (Equation (6.15)), element A will be moving fastest

and element C slowest. As element C moves down, it must warm up and

this requires heat. Thus, the heat ﬂux out of the top of this element will

be less than that into the bottom, and the temperature gradient required

to conduct this heat will be less at the top of the element than at the

bottom. However, w is small in this part of the glacier, so despite the

The steady-state temperature proﬁle 125

Height above bed, m

−30 −20 −10

−0.10

−0.50

−0.25

−0.50

(a) (b)

Figure 6.6. Calculated temperature proﬁles in polar ice sheets.

(a) Accumulation zone. Vertical velocity is negative or downward. Parameters,

other than w, are the same for all curves. Dashed proﬁle labeled “R: w =−0.50”

is calculated from Equation (5.25) for w. (b) Ablation zone. Vertical component

of velocity is positive or upward. (Modiﬁed from Hooke (1977), Figure 3.

Reproduced with permission of The University of Washington.)

comparatively high temperature gradient here, this element does not

have to warm up very much and the change in temperature gradient

through it is small, as shown. Element B has a higher velocity, and the

temperature gradient is still comparatively high here, at mid-depth in

the glacier, so this element must warm up a lot. Thus, here the change

in temperature gradient through the element is rather large. Element A

has the highest vertical velocity, but at this level in the glacier nearly

all of the heat introduced at the base has been consumed in warming

deeper ice. Thus, the temperature gradient here is quite low, and despite

126 Temperature distribution in polar ice sheets

Geothermal

heat

Bed

Depth

Surface

CCold

Figure 6.7. Qualitative

illustration of effect of

downward vertical velocity

on a temperature proﬁle.

its high velocity, element A does not have to warm up very much. Thus,

again, the change in temperature gradient through the element is small,

as shown.

Later we will examine temperature proﬁles in the ablation area,

where the vertical velocity is upward. However, the reader may ﬁnd

it both challenging and instructive to try to deduce the character of the

proﬁle there, using the logic just presented.

Error introduced by the assumed vertical

velocity distribution

One of the most tenuous assumptions we made in deriving

Equation (6.24)was that the longitudinal strain rate, ∂u/∂x,was inde-

pendent of depth. This led to the use of a linear decrease in w with

depth (Equation (6.15)) in Equation (6.16). As discussed in Chapter 5,

we know that ∂u/∂x decreases with depth under most conditions. Early

attempts to use a more realistic relation for w were made by Philberth

and Federer (1971) and Budd et al.(1971), but they relied on ad hoc

relations without good theoretical basis.

It would be convenient if we could simply use either Equation (5.24)

or Equation (5.25) for w,but this leads to solutions for β that cannot be

integrated a second time. Thus, a numerical integration is necessary.

To illustrate the importance of this effect, let us use Equation (5.25)in

place of Equation (5.21) for w. The solution for the temperature gradient

is then:

dθ

= β

−ξ z

(6.28)

where ξ = b

/3κH

. Integrating this numerically with w = b

=−0.5ma

−1

yields the dashed curve in Figure 6.6a. Thus, using this

Temperature proﬁles near the surface of an ice sheet 127

more realistic expression for w leads to basal temperatures that are nearly

◦

Cwarmer than given by Equation (6.24) for otherwise similar con-

ditions!

Temperature proﬁles in the ablation zone

In the ablation area, except very near the equilibrium line, w is posi-

tive, or upward. In this case, the solution for the temperature gradient

becomes:

dθ

= β

(6.29)

Again, this equation cannot be integrated in closed form, and the inte-

gral has not been tabulated. Examples of proﬁles obtained by a numerical

integration are shown in Figure 6.6b.Ofparticular interest is the expo-

nential increase in gradient near the surface, a result that is apparent

from Equation (6.29). A consequence of this behavior is that basal tem-

peratures must commonly reach the melting point in the ablation zone,

even with modest ice thicknesses and vertical velocities. Furthermore,

when basal temperatures do reach the melting point, β

becomes small,

so most of the geothermal heat is trapped at the bed resulting in high

basal melt rates.

Temperature proﬁles near the surface

of an ice sheet

Earlier (p. 122) we noted that although the temperature at the surface, θ

varies seasonally, the temperature at a depth of ∼10 m is very close to the

mean annual temperature. Let us now verify this. We adopt a coordinate

system with z = 0atthe surface and the z-axis pointing downward.

At the surface we assume that the seasonal variation can be described

by θ(z = 0, t) =

sin(ωt), where θ

is the annual temperature range

(twice the amplitude). Beneath the surface, we expect the oscillations

to be damped. Let the annual temperature range at depth be denoted by

(z) = θ

max

(z) − θ

min

(z). Our goal is to calculate the depth at which

 decreases to an acceptably small value. Then, we can measure the

temperature at this depth and use it as our boundary condition at the

surface.

Ignoring horizontal gradients, strain heating, and vertical advection

(so there is no accumulation, ablation, or compaction), Equation (6.13)

simpliﬁes to:

∂θ(z, t)

∂t

= κ

∂

θ(z, t )

∂z

(6.30)

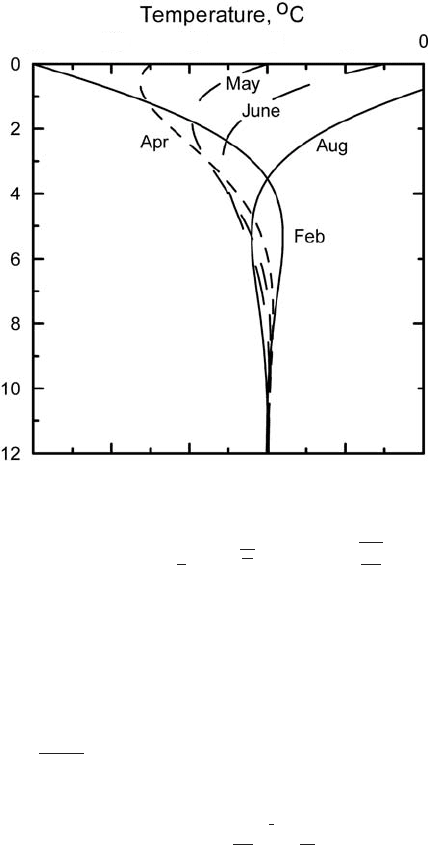
128 Temperature distribution in polar ice sheets

Depth, m

−25 −20 −15 −10 −5

Figure 6.8. Seasonal

variation in near-surface

temperature proﬁles in the

dry-snow zone of an ice sheet.

The solution to this is:

θ(z, t ) =

−z

√

2κ

sin



ωt − z



2κ



(6.31)

where ω is the period of the variation (in this case, 2 radians per year)

(Carslaw and Jaeger, 1959,p.65). If the seasonal variation in temperature

at the surface is sinusoidal, the temperature proﬁle at any given time

during the year can be calculated from Equation (6.31). Some proﬁles

for representative times are shown in Figure 6.8.

Now at any given depth, θ

max

(z,t) and θ

min

(z,t) occur when

ωt − z



ω/2κ =±/2, respectively. Thus, using Equation (6.31)to

obtain θ(z,t)atthese two times, and solving for z yields:

z =



2κ





(6.32)

From this we ﬁnd that z = 10 m if κ = 16 m

−1

,avalue appropriate

for unpacked snow, and  is 1.2% of θ

.Inice, with κ = 37.2 m

−1

z = 15.2 m. Thus, temperatures measured at a depth of 10 m in snow

and ﬁrn or 15 m in ice should closely approximate the mean annual

temperature.

The most serious assumption in this calculation is that accumulation

and ablation can be ignored. In the accumulation area, accumulating

snow insulates the surface, reducing θ

. This is probably not too serious

a problem. However, in the ablation area, as noted earlier, there is not

Temperature proﬁles near the surface of an ice sheet 129

only the insulating effect of snow during the fall and winter, but also

warming by percolating meltwater in the late spring or early summer

and then lowering of the ice surface later in the summer. Combined,

these processes result in 15 m temperatures that are likely to be warmer

than the mean annual temperature, as noted.

Equation (6.32) can also be used to calculate effects of temperature

oscillations over longer time spans. For example, oxygen isotope vari-

ations in ice cores have revealed temperature cycles during the Pleis-

tocene that have a range ∼5

◦

C and a period of ∼2000 years. These

cycles were discovered by Dansgaard and Oeschger (1989) and are called

Dansgaard–Oeschger cycles (see also Dansgaard et al., 1993). Their

cause is not yet understood. With κ = 38 m

−1

,avalue appropriate

for ice at −10

◦

C, and a more liberal  of 0.05θ

, z = 466 m. Thus,

such cycles would affect basal temperatures signiﬁcantly only near the

margin where the ice was less than ∼500 m thick.

The speed, ˆw,ofpropagation of a temperature maximum or mini-

mum resulting from such a sinusoidal cycle of temperature is (2ωκ)

1/2

and the time lag between the maximum at the surface and the maximum

at some depth, z,isthus, z/ ˆw.Inthe case of the Dansgaard–Oeschger

cycles, the speed would be about 0.49 m a

−1

, and the signal would reach

a depth of 466 m after about 950 years.

Let us now consider the temperature proﬁle in the ﬁrn area some

distance from an ice divide, a problem studied by Robin (1970). We

will restrict the problem to two dimensions; assume that strain heating is

negligible; and ignore conduction as K is low in ﬁrn, while the advective

terms are signiﬁcant. Equation (6.13) then becomes:

∂θ

∂t

=−u

∂θ

∂x

− w

∂θ

∂z

(6.33)

∂θ/∂t may be thought of as being composed of two parts, a thickening

or thinning of the ice sheet with time, and climatic change, thus:

∂θ

∂t

= λ(˙ε

H + b

) +

∂θ

∂t

Here, ε˙

H represents the change in thickness of the ice sheet by ﬂow (or

vertical strain), b

represents thickening by accumulation, and the differ-

ence between them is the net change in surface elevation. Multiplication

by the lapse rate, λ,orrate of decrease in temperature with increasing

elevation yields the resulting change in temperature at the glacier sur-

face. (As ε˙

is normally compressive, or negative, in an accumulation

zone, ε˙

H will be a negative number; b

is positive. If (ε˙

H + b

) turns

out to be negative, representing net thinning, multiplication by the neg-

ative lapse rate yields a positive ∂θ/∂t.) To this is added any change in

temperature due to secular climatic change, ∂θ

/∂t.

130 Temperature distribution in polar ice sheets

n(e

H + b

)

nua

Figure 6.9. Interpretation of

terms in Equation (6.34).

The expression u · ∂θ/∂x represents the change in temperature at the

glacier surface as the ice ﬂows to lower elevations; ∂θ/∂x can thus be

replaced with αλ,where α is the surface slope of the glacier. Finally, w

is equated with the accumulation rate, b

. Making these substitutions in

Equation (6.33) yields:

λ(˙ε

H + b

) +

∂θ

∂t

=−uαλ − b

∂θ

∂z

(6.34)

The meaning of the terms in Equation (6.34) can be clariﬁed by reference

to Figure 6.9.Aparticle of snow deposited at A has moved to B after n

years, and is buried under nb

meters of new accumulation. In the absence

of conduction, it is still at the temperature at which it was deposited at

A. The surface above B was at C when the snow was deposited at A and,

owing to the lapse rate, snow then accumulating at C was nuαλ degrees

warmer than that which was accumulating at A.Inaddition, the ice sheet

has thinned by an amount n(ε˙

H + b

)over the intervening years, and

the surface is now at D,which is n(ε˙

H + b

)λ degrees warmer than C.

Finally, there may have been secular climatic warming at a rate ∂θ

/∂t,

so snow at D is n ∂θ

/∂t warmer than it would be otherwise. Thus the

surface at D is:

nuαλ + n(˙ε

H + b

)λ + n

∂θ

∂t

warmer than the ﬁrn at B.Toobtain the temperature gradient from B to

D,divide by nb

and cancel the ns, thus:

∂θ

∂z

uαλ + (˙ε

H + b

)λ +

(

∂θ

/∂t

)

(6.35)

which, with minor manipulation, can be shown to be the same as Equation

(6.34).

When one is far from the edge of an ice sheet, it is very difﬁcult

to determine whether the ice sheet is thickening or thinning; that is,

whether (ε˙

H + b

)ispositive or negative. One can measure b

in snow

pits; the problem is to measure ε˙

without a stationary base upon which

to establish a survey point. Furthermore, such observations would span