Hooke R.L. Principles of glacier mechanics

Подождите немного. Документ загружается.

Fracture 71

Crack

Crack tip

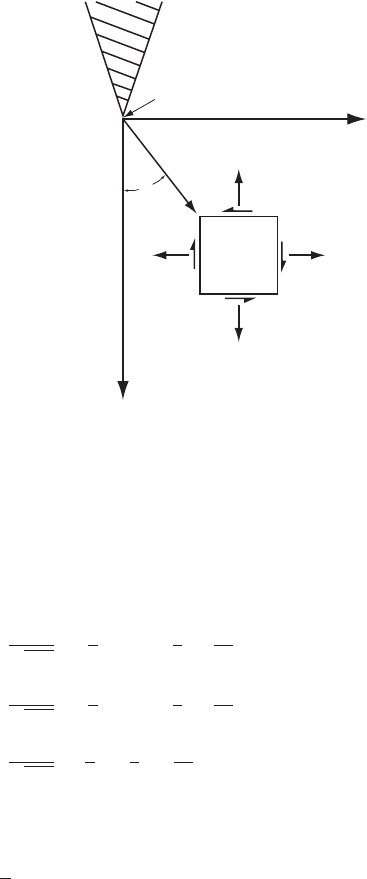
Figure 4.19. Stress ﬁeld on

an inﬁnitesimal element

located a distance r from a

crack tip. (Modiﬁed from

Kenneally, 2003.)

materials, and any far-ﬁeld stresses on the material are ampliﬁed at the

tips of these cracks. Thus, cracks may propagate at stresses far below

the strength of an unﬂawed specimen of the material.

The elastic stress ﬁeld around the tip of a vertical crack in the surface

of a solid of inﬁnite horizontal extent, subjected to a far-ﬁeld tensile

stress, σ , that is normal to the crack, is given by:

√

2r

cos



1 +sin

sin

3θ



√

2r

cos



1 −sin

sin

3θ



(4.11)

√

2r

sin

cos

3θ

(see, for example, Lawn, 1993,p.25). Here, r is the distance from the

crack tip measured along a line making an angle θ with the crack axis

(Figure 4.19), and K

is a parameter known as the stress intensity factor.

In general, K

= βσ

√

a,where a is the crack length. Thus, K

increases

as either the far-ﬁeld stress or crack length increase. The β is a geo-

metrical parameter that, in our case, depends upon factors such as the

spacing of crevasses, the ice thickness, and the far ﬁeld stress. Thus, K

and particularly β, describe how the far-ﬁeld stresses are ampliﬁed or

intensiﬁed around a crack tip.

Clearly, high values of K

translate into high stresses around the crack

tip and, if the stresses become high enough, the crack will propagate.

Rather than express this critical value in terms of the stresses themselves,

72 Flow and fracture of a crystalline material

500 600 700 800 900

Ice density,

kg m

−3

0.4 0.3 0.2 0.1 0.0

180

160

140

120

100

Critical stress intensity factor, K

, kPa m

1/2

Porosity

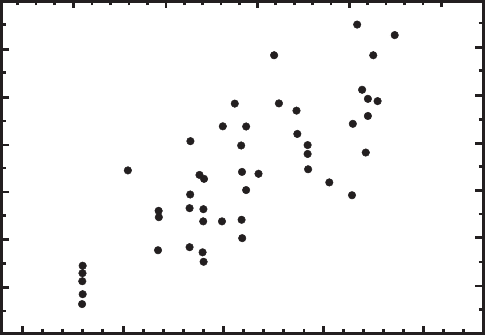
Figure 4.20. Variation of K

with density. Based on

laboratory measurements.

(After Rist et al., 1999.

Reproduced with permission

of the authors and the

American Geophysical Union.)

the standard procedure is to express it in terms of a value of K called the

fracture toughness, K

. K

is a material property of the medium. If K

exceeds K

, the fracture will propagate unstably. Rist et al.(1999)have

summarized their own measurements of K

on ice cores from Antarctica

and other workers’ measurements on other types of samples and ﬁnd that

it increases approximately linearly with density (Figure 4.20). The scatter

in the data is large, however.

Stress intensity factors are complicated and often tedious to derive,

but they can be obtained from handbooks such as Sih (1973). Conve-

niently, they obey the principal of superposition; thus, in problems with

a complex stress conﬁguration, if one can obtain stress intensity factors

for each of the stresses separately, they can be added to obtain the stress

intensity factor for the whole problem (Kanninen and Popelar, 1985,

p. 27). We will illustrate this below.

The alert reader may have noticed that the stresses in Equations (4.11)

become inﬁnite as r →0. However, deformation in a region immediately

around the crack tip is plastic, and this keeps the stresses ﬁnite. To

estimate the radius, r

,ofthis plastic region, take θ = 0inthe ﬁrst or

second of Equations (4.11), assume that plastic behavior will occur once

the stress exceeds 0.1 MPa (a commonly cited plastic “yield strength” for

ice), adopt a value for K

of 0.16 MPa m

−1/2

, and solve for r

. The result

is r

≈ 0.4 m. The principles of linear elastic fracture mechanics only

apply if r

is small compared with a.Asweare concerned principally

Fracture 73

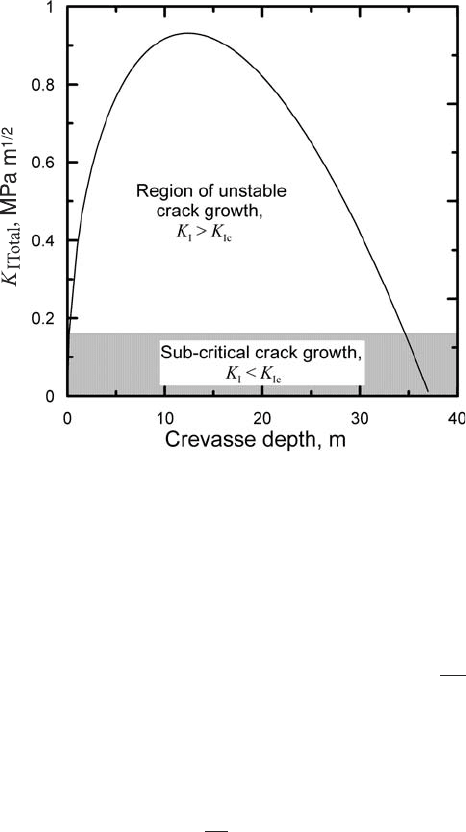
Figure 4.21. Variation in

stress intensity factor with

crevasse depth for an air-ﬁlled

crevasse formed by a tensile

stress of 0.2 MPa. (Modiﬁed

from Kenneally, 2003.)

with crevasses, and as most crevasses reach depths of at least 10–20 m,

this condition is satisﬁed.

Let us consider the case of a single crevasse in a glacier of inﬁ-

nite horizontal extent subjected to a tensile stress, σ .Two stresses are

involved: the tensile stress that tends to open the crack and the weight

of the overlying ice that tends to squeeze it closed. We need a stress

intensity factor for both. For the case of a crack of depth d in a medium

of thickness H  d subjected to a tensile stress, σ , K

= 1.12σ

√

πd

(Kanninen and Popelar, 1985,p.31). The subscript “t” signiﬁes tension.

The hydrostatic stress from the weight of the ice is −ρ

gz,where ρ

is the

density of ice, g is the acceleration of gravity, and z is the depth below

the surface. The negative sign indicates that the stress is compressive.

Foracrack of depth d with a load varying from 0 at the surface to −ρ

at the crack tip, K

=−0.683ρ

√

d (Kenneally, 2003). Here, the

subscript “o” is used for overburden. Vaughan (1993) found that tensile

stresses between 0.09 and 0.32 MPa were necessary to open crevasses.

(These are considerably lower than the stresses bounding the fracture

ﬁeld in Figure 4.16, probably because glacier ice has more and deeper

surface ﬂaws that can develop into crevasses.) For purposes of illustra-

tion, let us assume σ = 0.2 MPa. K

ITotal

= K

+ K

then varies with

crevasse depth as shown in Figure 4.21.

From Figure 4.21,wesee that once a crack ∼0.16 m long is formed,

ITotal

exceeds K

and the crack will propagate unstably to a depth

74 Flow and fracture of a crystalline material

of ∼35 m. The depth, of course, depends on σ ,but this is a realistic

depth for crevasses.

Of considerable interest in view of the recent collapse of the Larsen

B Ice Shelf mentioned in Chapter 3,isthe effect of water on crevasse

depth. By analogy with the K

above, the stress intensity factor for

stresses induced by water pressure in a crevasse that is ﬁlled with water is

= 0.683ρ

√

d,where ρ

is the density of water. K

is positive

because the water pressure tends to open the crevasse. Because ρ

>ρ

ITotal

,which now includes K

, increases continuously with depth. Thus,

once it exceeds K

,itnever drops below K

again, and the crevasse will

penetrate to the bed.

Three additional factors that inﬂuence crevasse depth are: (1) the

presence of low-density ﬁrn at the surface, (2) the water level in the

crevasse if it is not ﬁlled, and (3) the effect of other crevasses. In all

three cases, the consequences of taking these factors into consideration

are fairly obvious. Low-density ﬁrn reduces K

so crevasses penetrate

deeper; if there is not enough water in the crevasse, K

will not exceed

and the crevasse may not penetrate to the bed; and if there is a ﬁeld

of crevasses, the tensile stress will be relieved by adjacent crevasses

and no one crevasse will penetrate as deeply as would a single crevasse.

Stress intensity factors can be obtained for these three situations (Van

der Veen, 1998), but the algebra, while straightforward, becomes con-

siderably more complicated and is beyond the scope of this book.

Summary

In this chapter we ﬁrst reviewed the crystal structure of ice, and noted that

there are imperfections in this structure, called dislocations, that allow ice

(and other crystalline materials) to deform under stresses that are low

compared with the strength of individual molecular bonds. Processes

that may limit the rate of deformation are those which (1) inhibit motion

of a dislocation in a single crystallographic plane (drag), (2) prevent

dislocations from climbing from one crystallographic plane to another

to get around tangles, (3) impede motion on certain crystallographic

planes, and (4) inhibit adjustments of boundaries between crystals.

Experimental data do not, at present, provide a basis for choosing

between these possible rate-limiting processes. However, the drag mech-

anism does provide a theoretical basis for the commonly observed value

of the exponent, n,inthe ﬂow law (see Equation 4.4). Perhaps equally

important, however, are the mechanisms that allow adjustment of grain

boundaries.

Because some crystals in a polycrystalline aggregate are not ori-

ented for easy glide, stress concentrations develop. These result in

Summary 75

recrystallization by three distinct processes: grain growth, polygoniza-

tion, and nucleation of new grains. Recrystallization leads to preferred

orientations of c-axes, and hence to more rapid deformation. The prin-

cipal processes involved in the development of these fabrics appear to

be nucleation of new grains and rotation of grains as slip occurs on their

basal planes.

To place the creep processes in ice in a more general framework,

we introduced a deformation mechanism map in which we displayed the

range of temperatures and stresses under which different deformation

processes occur. Within the temperature and stress ranges normally found

in glaciers, power-law creep is likely to be the dominant process although

diffusional creep may occur in some low stress situations.

Next, we introduced Glen’s ﬂow law, and related the exponent, n,in

the ﬂow law to the creep mechanisms discussed earlier. Then we con-

sidered how temperature, pressure, texture, fabric, and water content

affect the viscosity parameter, B.Temperature and pressure effects may

be incorporated into the ﬂow law by rigorous, physically based modi-

ﬁcations, whereas ad hoc procedures based on empirical evidence are

used to incorporate the other effects.

Finally, we introduced principles of linear elastic fracture mechanics

and demonstrated that these principles can be used to estimate crevasse

depths.

Chapter 5

The velocity ﬁeld in a glacier

Many problems in glaciology require an understanding of the ﬂow ﬁeld

in a glacier. For example, the way in which ﬂow redistributes mass deter-

mines the shape of a glacier, and also the rapidity with which glaciers

respond to climatic change. Flow also redistributes energy and thus

affects the temperature distribution. This, in turn, has important impli-

cations for the nature of the coupling with the glacier bed. Spatial vari-

ations in speed, or strain rates, are of concern to structural geologists

using glaciers as analogs for deformation of rocks. From a geomorphic

perspective, the entrainment of debris and the character of moraines

constructed from this debris are dependent upon the ﬂow ﬁeld. In short,

understanding the ﬂow ﬁeld is fundamental to the analysis of many prob-

lems in glacier mechanics.

Forafull description of the ﬂow ﬁeld in a glacier, we need the

horizontal and vertical components of the velocity at every point. By

making several assumptions, we can obtain approximate solutions to this

problem that will give insights into certain characteristics of glaciers and

the landforms they produce. Initially, we will limit the analysis to two

dimensions and also assume a steady state.

We will begin by studying the distribution of horizontal velocity.

Given the pattern of accumulation and ablation over a glacier, we can use

conservation of mass to determine the mean (depth-averaged) horizon-

tal velocity. Then, by using conservation of momentum and a simpliﬁed

version of the ﬂow law (Equation (4.5)), we will consider the variation

in horizontal velocity with depth in an ice sheet and in a valley glacier.

Differences between these solutions and measured velocity distributions

reveal inadequacies of the theory, and draw attention to the need for a

Measurement of velocity 77

better understanding of the basal boundary condition. Finally, by inte-

grating the velocity over depth, we calculate the mass ﬂux, and also obtain

an expression for the mean velocity in terms of the glacier thickness.

The vertical velocity ﬁeld is treated next. Again we will use the

steady-state assumption and the pattern of mass balance (conservation

of mass) to determine the vertical velocity at the surface. We then use the

longitudinal strain rate, or rate of stretching in the longitudinal direction,

at the surface to estimate its variation with depth, and thus calculate the

variation in vertical velocity with depth. This yields an approximation

to the full velocity ﬁeld.

Next, we discuss the role of drifting on the ﬂow ﬁeld, and show that

drifting patterns at the surface of an ice sheet can be traced at depth using

radio echo sounding techniques. Drifting also affects the topography of

a glacier surface, and plays an important role in the formation of certain

types of moraine. Finally, we will explore inhomogeneous ﬂow in ice

sheets, as manifested by ice streams.

Measurement of velocity

Before describing the velocity ﬁeld, a brief overview of measurement

techniques may be helpful. In the early days of glaciology, velocity

measurements were commonly made by triangulation from ﬁxed points

on stable surfaces off of the glacier. I have spent many hours peer-

ing through a theodolite at stakes drilled into a glacier. In the 1970s,

electronic theodolites with laser distance-ranging capabilities greatly

reduced the effort needed to make a measurement. Because the distance

can be measured directly with such an instrument, a stake location can

be determined by occupying only one ﬁxed point rather than two, and

electronic display of angles saves hours of adjusting a vernier. Later

technological developments have resulted in computer-driven systems

that can activate the theodolite and track the stakes. Thus, measurements

can be made automatically as often as desired.

Velocity measurements far from stable ﬁxed points are next to impos-

sible with theodolite-based techniques. The advent of geographical posi-

tioning systems (GPS) technology solved that problem. GPS units mea-

sure the distance to a ﬂeet of satellites with orbits that are known very

accurately. With the most precise GPS units, the location of a point can

be determined to within a couple of centimeters. Such units are now used

to measure rates of continental drift.

An exciting development that is quickly leading to a much better

understanding of ﬂow ﬁelds in large ice sheets is the use of satellite

images taken at, say, intervals of days to a year or so, to determine the

velocity ﬁeld. The images are coregistered based on the assumption that

78 The velocity ﬁeld in a glacier

(x)

h(x)

Figure 5.1. Schematic

diagram illustrating

dependence of

u on b

on an ice sheet.

certain features are stationary or moving only slowly compared with

others. Then, cross-correlation techniques are used to compare crevasse

patterns or other recognizable moving features on the two images and to

determine how far they have moved between the dates of the respective

images (Bindschadler and Scambos, 1991; Whillans and Tseng, 1995).

High-speed digital computers are used to make these comparisons. In this

way,adetailed quantitative map of the ﬂow ﬁeld can be produced. This

technique, called satellite interferometry, is revolutionizing the measure-

ment of velocities that, a scant 35 years ago, could be obtained only by

tedious precision surveying with a theodolite.

Balance velocity

The general pattern of ﬂow in a glacier is determined by the net budget.

Consider an idealized glacier which, over a period of years, is in a steady

state so its thickness (or surface proﬁle) does not change. Then, at some

distance, x, from the divide, the mean horizontal velocity averaged over

depth is:

u =

h(x)



(x ) dx (5.1)

where h(x)isthe glacier thickness, and for convenience, the units of b

are taken to be meters of ice per year (Figure 5.1). This equation is an

expression of the principle of conservation of mass in an incompressible

medium. As much mass must be moved out of the control volume, V,by

ﬂow,

uh(x), as enters it by accumulation on the surface,



(x) dx. The

velocity

u is called the balance velocity.

Balance velocities on the Antarctic ice sheet are shown in Figure

5.2.Tocalculate these velocities, Huybrechts et al. (2000) used detailed

maps of the surface and bed elevations to obtain ice thicknesses at nearly

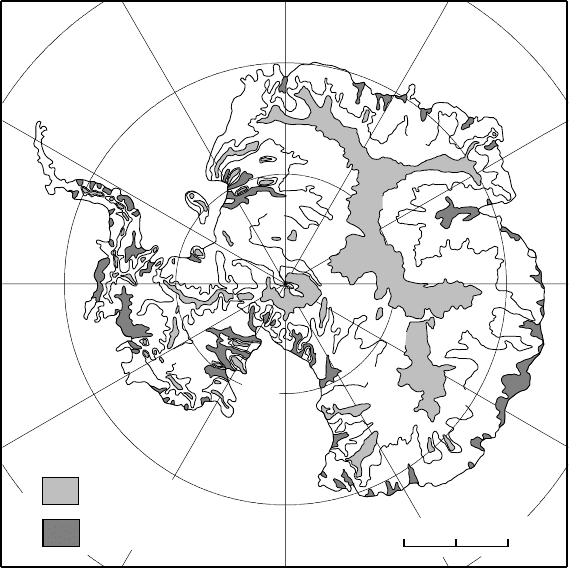
Shear stress distribution 79

1000 km

> 100 m a

−1

< 2 m a

−1

Ice

shelf

Ice

shelf

Figure 5.2. Balance

velocities on the Antarctic ice

sheet. (Modiﬁed from

Huybrechts et al., 2000,

Figure 4. Reproduced with

permission of the author and

the International Glaciological

Society.)

80 000 points of a grid. They then used the surface elevations to calculate

surface slopes, and hence directions of ice ﬂow. This allowed the calcu-

lation of balance velocities, using a two-dimensional form of Equation

(5.1)totake convergence and divergence of ﬂow into consideration. Ice

divides show up well on the map as regions of essentially zero velocity.

Note also the general increase in velocity toward the coast, and the focus-

ing of ﬂow into relatively narrow zones near the coast. Because most of

the ice loss from Antarctica is by calving, there is no decrease in velocity

near the coast as there would be if ice were lost by melting in an ablation

zone of appreciable width.

Shear stress distribution

To determine the velocity distribution at depth in a glacier, we will ﬁnd,

below, that we need an expression for σ

as a function of z. Thus, we

digress brieﬂy from the principal objectives of this chapter to derive two

similar expressions for σ

that are commonly used in the literature. The

derivations differ only in the orientation of the axes and of the plane on

which σ

operates.

80 The velocity ﬁeld in a glacier

(a)

(b)

∆ x

∆h

Figure 5.3. Derivations of

two alternative expressions for

the shear stress, σ

,ona

plane at depth h.

Consider, ﬁrst, the situation in Figure 5.3a. The origin is at the sur-

face. The x-axis is taken parallel to the surface, which slopes at an angle

α. The z-axis points downward, normal to the surface. We want the

shear stress on a plane at depth h. The column of ice is taken to be 1 m

on a side. Therefore, the weight of the column is ρgh,where ρ is the

density of ice and g is the acceleration due to gravity. The component of

that weight parallel to the plane of interest is, thus, ρgh sin α.For static

equilibrium, this must be balanced by a shear stress on the plane, so:

=−ρgh sin α. (5.2a)

The shear stress is negative because it acts in the negative x-direction

on a plane with an outwardly directed normal in the positive z-direction

(see p. 5 and Figure 2.3).

Next, consider the situation in Figure 5.3b. The x-axis is now hori-

zontal and the z-axis is vertical. Again, the origin is on the surface and the

column is of unit cross-sectional area. On the right side of the column,

the plane of interest is at depth h below the surface. To a good approxi-

mation, the hydrostatic (or lithostatic) pressure at this depth is ρgh and

the pressure varies linearly with depth. Thus, the mean pressure is

ρgh,

and the force on this side is

ρgh h,where the second h represents the

area of the face. Similarly, on the left side, the force is

ρg(h + h)

The force on the plane of interest is −σ

x. Summing forces on the

column yields:

ρg

(

h + h

)

−

ρgh

− (−σ

x ) = 0

Expanding the ﬁrst term, neglecting the term in h

, noting that tan

α = h/x, and rearranging terms leads to:

=−ρgh tan α (5.2b)

This equation is appropriate for a situation in which both the x-axis and

the plane of interest are horizontal, but the glacier surface is sloping.