Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel

Подождите немного. Документ загружается.

361

Работа этих функций вполне очевидна и нет необходимости комментировать ее

более подробно. Функции этого класса применяются в программах или для

контроля переменных.

A.3.9 Функции пользователя и рекурсивные функции

Функции пользователя в Mathcad задаются в виде:

Имя(Список_параметров):=Тело_функции

Список параметров задается перечнем переменных, отделенных запятыми. Эти

переменные являются локальными, т.е. действуют в пределах тела функции.

Примеры задания функций:

fun(x) := 5





exp(x))

module(x,y) :=

yx 

Mathcad допускает внутри тела функции пользователя задавать обращение к

самой этой функции. Это означает возможность задания рекурсивных функций,

порой заметно упрощающих реализацию различных алгоритмов. Функция if также

позволяет создавать рекурсивные алгоритмы:

fact(n) := if(n=0, 1, n



fact(n-1)) fact(0) = 1 fact(5) = 120

Этот пример носит чисто познавательное значение, поскольку Mathcad имеет

оператор – функцию вычисления факториала n!. Другой пример задает функцию,

порождающую линейно спадающее периодическое пилообразное колебание P(x)

с периодом T:

F(x) := 1-x P(x) := if(x<T, F(x), P(x-T))

Хотя рекурсия – мощный математический прием, в большинстве случаев более

эффективным является решение задач без ее применения.

Применение операторов и функций позволяет создавать документы, вид которых

вполне привычен для математиков и тех, кто ее применяет. Это видно из

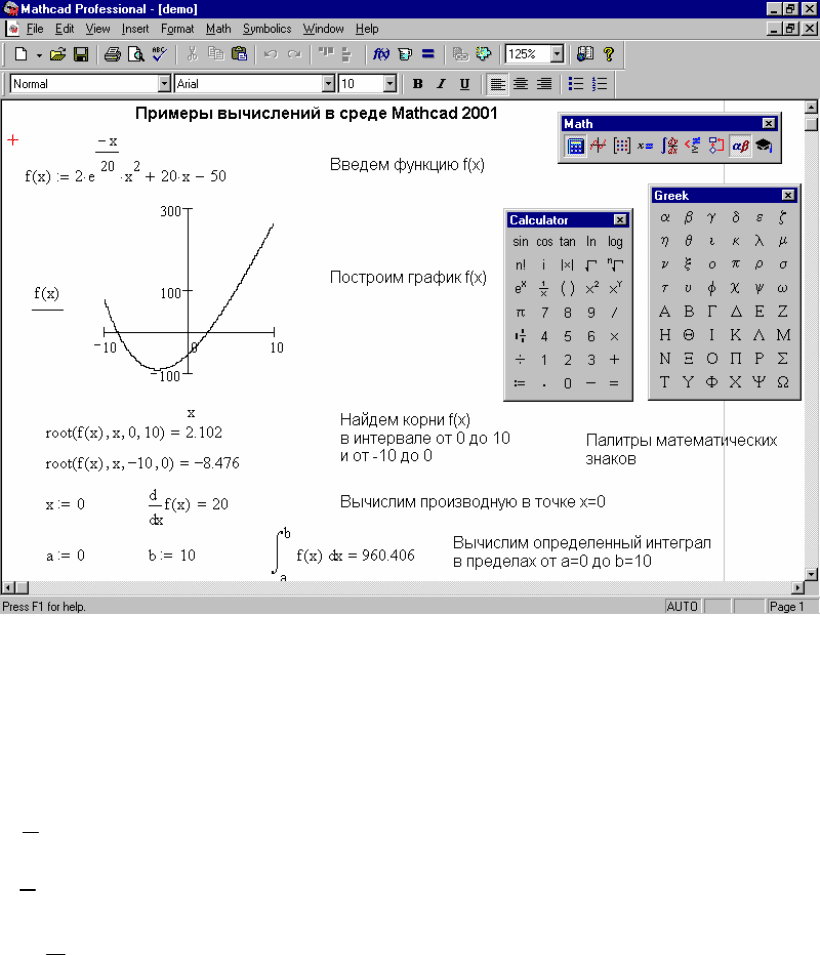
примеров, представленных на рисунке A.13. Здесь показано задание функции f(x),

построение ее графика, вычисление корней, производной в заданной точке f(x) и

определенного интеграла в заданных пределах.

362

c 212 degF





100

degC



C T( )

273.15















k t( ) t 273.15







Рисунок A.13 – Примеры работы с заданной функцией пользователя

Функции пользователя удобны и для задания некоторых функций преобразования

одних величин в другие. Ниже представлены примеры на преобразование

температуры из градусов Целия в грудусы Фаренгейта и наоборот, а также

градусов Сельсия в градусы Кельвина и наоборот:

Первая колонка задает функции пользователя для таких преобразований, а две

другие колонки дают примеры преобразований. Эти преобразования широко

используются в практике химических и физических расчетов. В этих вычислениях

используется техника работы с размерными величинами. Важно обратить

внимание на задание размерных констант после блока вычислений. Это задание

может выполняться в любом месте документа.

Самым распространенным химическим веществом является воздух из которого

состоит атмосфера Земли. Для многих химических реакций и существования

биологических объектов важное значение имеет давление воздуха и его

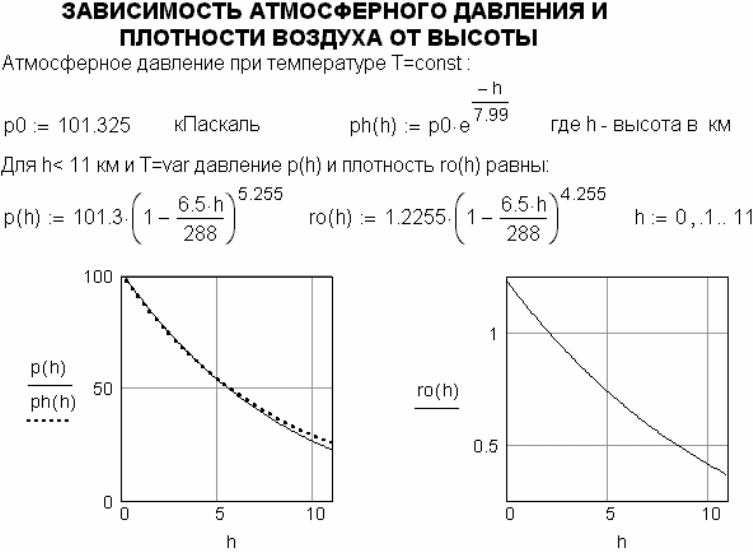
плотность. Рисунок A.14 показывает применение функций пользователя для

вычисления этих параметров по известным эмпирическим формулам.

f c( )

c



f 0 degC





degF



f 21 degC





69.8

degF



c f( )

f 32

 



c 100 degF





37.778

degC



C 373.15 K





100

degC



C 400 K





126.85



k 100 degC





373.15



k 21 degC





294.15



degF



degC



363

Рисунок A.14 – Вычисление давления и плотности атмосферного воздуха в

функции от высоты

A.4 Работа с массивами, векторами и матрицами

A.4.1 Типы массивов и доступ к их элементам

Массивы – важный тип множественных данных с доступом к любому его

элементу. Mathcad работает с одномерными массивами – векторам и двумерными

– матрицами. Массивы могут содержать как числовые, так и символьные данные.

В Mathcad 2000 векторы и матрицы отображаются длинных скругленных скобках.

Каждый элемент массива представлен индексированной переменной с одним

целочисленным индексом для вектора или двумя для матрицы (например M

1,1

или

2,2

). Нижняя граница индексации определяется системной переменной ORIGIN,

которая может принимать значение 0 или 1 (по умолчанию 0). Для ввода индекса

используется знак " [ " – прямая открывающая скобка.

С элементами массивов (векторов и матриц) можно работать как с обычными

переменными, т.е. присваивать им значения с помощью оператора присваивания

:= и выводить на индикацию с помощью оперераторов вывода = или . С

помощью векторов и матриц можно обеспечить множественное присваивание

переменным значений:

Не следует путать индексированные переменные со скалярными переменными с

индексом в имени переменной. Например, ток I1, где нижний индекс имени

означает просто «первый ток», например – ток в ветви 1 некоторой электрической

схемы. Подобные индексы – индексы в имени переменной – вводятся с помощью















sin

1.0

 















y 10

0.841



364

точки, причем синий уголок маркера ввода при этом охватывает все имя, а не

только область ввода индекса.

Векторы и матрицы можно задавать путем ввода их элементов - индексированных

переменных. Для задания векторов и матриц можно воспользоваться операцией

Matrices... в позиции Math основного меню, нажатием клавиш “Ctrl”+”V” или

вводом пиктограммы с изображением шаблона матрицы. Это вызывает вначале

появление диалогового окна, в котором надо указать размер матрицы, т. е.

количество ее строк m и столбцов n.

A.4.2 Векторные и матричные функции

Существует также ряд встроенных векторных и матричных функций. Они

облегчают решение задач линейной алгебры и других сфер приложения векторов

и матриц.

Приведем основные векторные функции, входящие в систему Mathcad:

length(V) – число элементов вектора;

last(V) – номер последнего элемента;

max(V) – максимальный по значению элемент вектора (или матрицы);

min(V) – возвращает минимальный по значению элемент вектора (или матрицы);

Re(V) – вектор действительных частей вектора с комплексными элементами и

Im(V) – вектор мнимых частей вектора с комплексными элементами.

Примеры:

V := ( 2 6 3 4 1)

length(V) = 5 max(V) = 6 last(V) = 4 Re(V)

= (2 6 3 4 1)

Имеется также функция



(i, j, k), которая возвращает единичный полностью

антисимметричный тензор третьего ранга; i, j и k должны быть целыми числами

от 0 до 2 (или между ORIGIN и ORIGIN



2, если ORIGIN



0). Возвращает 0, если

любые два аргумента равны, 1 – если три аргумента являются четной

перестановкой (0, 1, 2), и -1, если три аргумента являются нечетной

перестановкой (0, 1, 2).

Для работы с матрицами также существует ряд встроенных функций:

augment(M1,M2) – объединяет в одну матрицы M1 и M2, имеющие одинаковое

число строк;

identity(n) – создает единичную квадратную матрицу размером n*n;

stack(M1,M2) – объединяет две матрицы M1 и M2, имеющие одинаковое число

столбцов, сажая M1 над M2;

submatrix(A,ir,jr,ic,jc) – возвращает субматрицу, состоящую из всех элементов,

содержащихся в строках от ir по jr и столбцов с ic по jc (ir



jr и ic



jc);

diag(V) – создает диагональную матрицу, элементы главной диагонали которой

равны элементам вектора V;

matrix(m,n,f) – создает матрицу, в которой (i, j)-й элемент равен f(i, j), где i=0, 1,.. m

и j=0, 1,.. n и f(i, j) – некоторая функция.

Следующие функции возвращают ряд важных характеристик матрицы M:

cols(M) – число столбцов;

rows(M) – число строк;

365

rank(M) – ранг;

r(M) – возвращает след (сумму диагональных элементов);

mean(M) – среднее значение элементов;

median(M) – медиана элементов;

cond1(M) – число обусловленности матрицы, вычисленное в норме L1;

cond2(M) – число обусловленности матрицы, вычисленное в норме L2;

condе(M) – число обусловленности матрицы в норме евклидового пространства;

condi(M) – число обусловленности матрицы в равномерной норме;

norm1(M) – L1 норма;

norm2(M) – L2 норма;

norme(M) – Евклидова норма;

normi(M) – неопределенная норма.

A.4.3 Дополнительные матричные функции

В профессиональные версии Mathcad (с приставкой PRO, а также в Mathcad 2001i)

включен ряд дополнительных матричных функций:

lu(M) – выполняет треугольное разложение матрицы M: P



M = L



U, L и U –

соответственно нижняя и верхняя треугольные матрицы. Все четыре матрицы

квадратные, одного порядка;

qr(A) – дает разложение матрицы A, A=Q



R, где Q – ортогональная матрица и R –

верхняя треугольная матрица;

svd(A) – дает сингулярное разложение матрицы A размером n



m: A=U



, где U

и V – ортогональные матрицы размером mm и nn соответственно. S –

диагональная матрица, на диагонали которой расположены сингулярные числа

матрицы A;

svds(A) – возвращает вектор, содержащий сингулярные числа матрицы A

размером m



n, где m



geninv(A) – левая обратная к матрице A. L



A=E, где E – единичная матрица

размером n



n, L – прямоугольная матрица размером n



m, A – прямоугольная

матрица размером m



Для решения проблемы собственных значений служат функции:

eigenvals(M) – вектор собственных значений матрицы M;

eigenvec(M,Z) – вектор, принадлежащий собственному значению Z матрицы M;

eigenvecs(M) – матрица, столбцы которой – собственные векторы матрицы M;

genvals(M,N) – вектор обобщенных собственных значений v

, соответствующий

решению уравнения M



x=v



x и genvals(M,N) – матрица, столбцы которой –

нормированные обобщенные собственные векторы.

Есть также функции сортировки элементов векторов и матриц:

sort(V) – сортировка возрастания значений;

366

reverse(V) – сортировка в порядке убывания;

csort(M,n) – перестановка строк матрицы M таким образом, чтобы

отсортированным оказался n-ый столбец;

rsort(M,n) – перестановка столбцов матрицы M таким образом, чтобы

отсортированной оказалась n-ая строка.

A.4.4 Решение систем линейных уравнений

Векторные и матричные операторы и функции системы Mathcad позволяют

решать широкий круг задач линейной алгебры. К примеру, если задана матрица A

и вектор B для системы линейных уравнений в матричной форме A



X=B, то

вектор решения можно получить из очевидного выражения X=A

-1



Для решения этой задачи есть и встроенная функция lsolve(A, B), которая

возвращает вектор X для системы линейных уравнений A – X=B.

A.5 Сохранение и использование данных

Mathcad может успешно использоваться в физических, химических и

измерительных установках для обсчета данных эксперимента. Для этого Mathcad

имеет специальный тип данных – файловые данные. Работу с ASCII файлами

дают следующие операции:

READ("Имя_файла") – считывает данные из файла с указанным именем (пример

применения V := READ("DATA")

WRITE("Имя_файла") – записывает данные в файл и присваивает ему указанное

имя например: WRITE("Имя_файла") := Выражение

APPEND("Имя_файла") – дописывает данные в конец уже существующего

файла. Нельзя использовать другие функции для дописывания данных - они

уничтожают прежние данные в файле и заносят новые данные.



Матрица комплексных коэффициентов системы линейных уравнений

4 i

0.09

0.04

0.24

0.08

0.15

4 i















Вектор свободных членов















Решение системы

1( )





1.787 0.468i

3.184 0.045i

4.75 1.184i















367

Функции READ, WRITE и APPEND в версиях Mathcad 8/2000/2001 сохранены

только ради совместимости с программами предшествующих версий Mathcad. Их

применение не рекомендуется, хотя и вполне возможно. Основными являются

функции:

READPRN("Имя_файла") – считывает данные в виде двумерного массива –

матрицы. 5. WRITEPRN("Имя_файла") – записывает матричное (или матрицу) в

файл с указанным именем.

APPENDPRN("Имя_файла") – дописывает данные в уже существующий

матричный файл.

READRGB("Имя_файла") – считывает изображение из файла формата RGB и

возвращает массив из трех подмассивов красного, зеленого и синего цветов.

Рисунок A.15 демонстрирует типовые операции с данными файлового типа. Этот

рисунок показывает эффективные возможности занесения данных в файл и затем

их считывания.

Рисунок A.15 – Основные операции с данными файлового типа

Полный набор функций для работы с данными файлового типа представлен

специальной литературе.

A.6 Проведение линейной и сплайновой аппроксимаций

A.6.1 Одномерная линейная аппроксимация

Часто зависимости вида y(x), представлены отдельными узловыми точками. При

кусочно-линейной интерполяции вычисления дополнительных точек выполняются

по линейной зависимости. Для этого используется функция linterp(VX, VY, x). Для

заданных векторов VX и VY узловых точек и заданного аргумента x linterp(VX, VY,

x) возвращает значение функции при ее линейной аппроксимации.

368

A.6.2 Сплайн-интерполяция и аппроксимация

Часто хорошие результаты дает сплайн-аппроксимация отрезками кубических

полиномов, проходящих через три смежные узловые точки. Коэффициенты

полиномов рассчитываются так, чтобы непрерывными были первая и вторая

производные. Линия, которую описывает сплайн-функция, напоминает по форме

гибкую линейку, закрепленную в узловых точках. Для осуществления сплайновой

аппроксимации система Mathcad предлагает следующие функции:

cspline(VX, VY) – возвращает вектор VS вторых производных при приближении в

опорных точках к кубическому полиному;

pspline(VX, VY) – возвращает вектор VS вторых производных при приближении к

опорным точкам к параболической кривой;

lspline(VX, VY) – возвращает вектор VS вторых производных при приближении к

опорным точкам прямой.

interp(VS, VX, VY, x) – возвращает значение y(x) для заданных векторов VS, VX,

VY и значения x.

Сплайн-аппроксимация проводится в два этапа. Вначале с помощью функций

cspline, pspline или lspline отыскивается вектор вторых производных функции y(x),

заданной векторами VX и VY ее абсцисс и ординат. Затем для каждой точки

вычисляется y(x) с помощью функции interp, показанной на рисунке A.16.

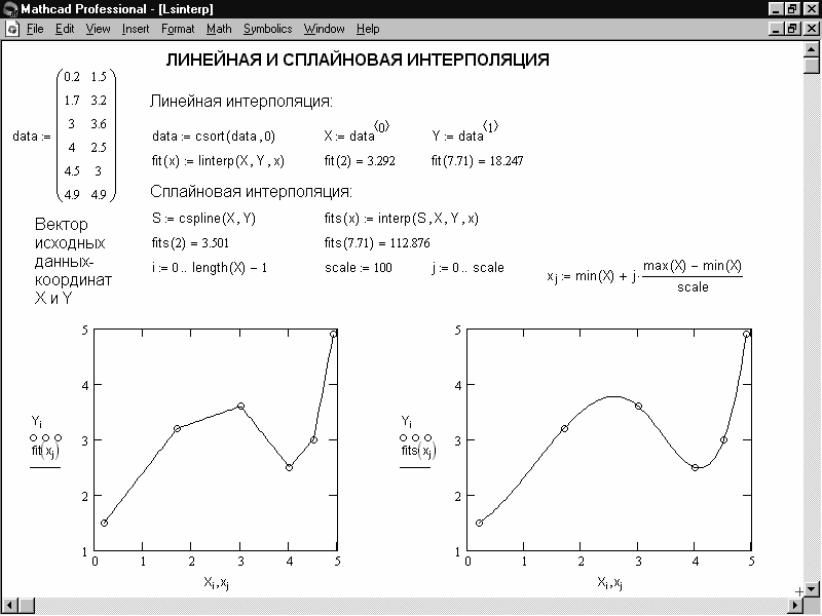
Рисунок A.16 – Линейная и сплайновая интерполяция функции, заданной таблично

Нетрудно заметить, что график при линейной интерполяции (аппроксимации)

оказывается слишком грубым – отчетливо видны точки перегибов. В то же время

сплайн-интерполяция, несмотря на малое число точек в этом примере (их всего

6), дает прекрасные результаты: график функции оказывается плавным и точки

его перегиба вообще незаметны.

369

A.7 Статистическая обработка данных

С помощью системы Mathcad можно проводить наиболее распространенные

статистические расчеты с данными, представленными векторами их значений.

Существует также ряд статистических функций для скалярного аргумента. С них и

начнем обсуждение статистических расчетов.

A.7.1 Типовые статистические функции

Помимо уже упомянутой гамма-функции, широко применяемой в статистических

расчетах, существуют следующие встроенные статистические функции

скалярного аргумента x:

cnorm(x) – кумулятивная нормальная функция;

erf(x) – функция ошибок (или интеграл вероятности);

rnd(x) – функция генерации случайных чисел с равномерным распределением;

corr(VX,VY) – коэффициент корреляции двух векторов – VX и VY;

cvar(X,Y) – коэффициент ковариации X и Y. Через функцию erf(x) легко

вычисляется дополнительная функция ошибок erfс(x) = 1– erf(x).

Следующая группа функций относится к вычислению основных статистических

параметров одномерного массива данных – вектора:

mean(V) – среднее значение;

var(V) – дисперсия (вариацию);

side(V) – среднеквадратичная погрешность (квадратный корень из дисперсии;

stdev(V) – стандартное отклонение;

hist(int,V) – возвращает вектор частот попадания данных V в заданные интервалы

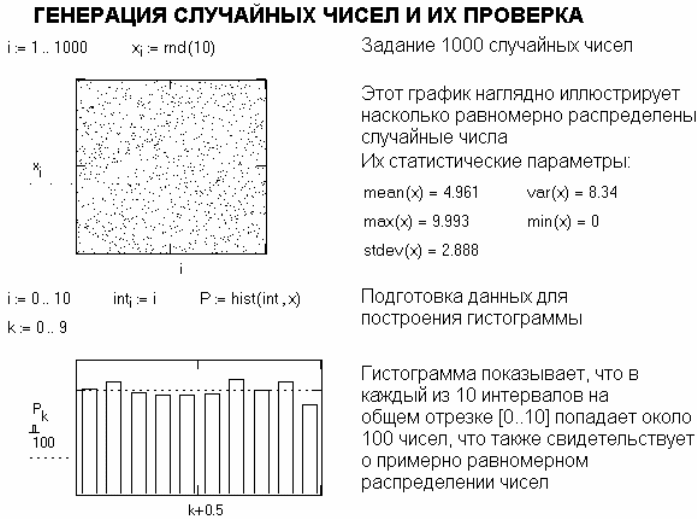
int (служит для построения гистограмм). На рисунке A.17 представлен документ, в

котором организована генерация вектора X из 1000 случайных чисел,

представлено их распределение и вычислены основные статистические

параметры массива случайных чисел – вектора X. Этот документ демонстрирует и

применение функции hist.

370

Рисунок A.17 – Работа со случайными числами

При достаточно большом числе случайных чисел вид гистограммы приближенно

говорит о законе их распределения.

A.7.2 Статистические функции для распределений вероятности

Функции для плотности вероятности распределения представлены следующим

набором:

dbeta(x, s1, s2) –



-распределение (s1, s2>0 – параметры формы, 0<x<1);

dbinom(k, n, p) – биномиальное распределение (возвращает значение вероятности

P(x=k), где n и k целые числа, причем 0  k  n и 0



1);

dcauchy(x, l, s) – распределения Коши (l – параметр разложения, s>0 –

параметр

масштаба);

dchisq(x, d) – Хи-квадрат-распределение (x, d>0, причем d –

число степеней

свободы);

dexp(x, r) – экспоненциальное распределение (r, x>0);

dF(x, d1, d2) – распределение Фишера (d1,d2 > 0 –

числа степеней свободы,

x > 0);

dgamma(x, s) – гамма-распределение (s>0 – параметр формы, x



0);

dgeom(k, p) – геометрическое распределение (0 < p



1 – вероятность успеха в

отдельном испытании, k – целое не отрицательное число);

dlnorm(x,





) – логнормальное распределение (



– натуральный логарифм

среднего значения,



> 0 – натуральный логарифм среднеквадратичного

отклонения, x > 0;

dlogis(x, l, s) – логистическое распределение (l –

параметр разложения,

s > 0 – параметр масштаба);

dnbinom(k, n, p) – отрицательное биномиальное распределение (n

> 0 и

k > 0 – целые числа, 0 < p



1);