Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.

371
dnorm(x,
,
) – нормальное распределение (
– среднее значение,
> 0 – среднеквадратичное отклонение);
dpois(k,
) – распределение Пуассона (
>0, k – целое не отрицательное число);
dt(x, d) – распределение Стьюдента (d > 0 – число степеней свободы,
x – вещественное число);
dunif(x, a, b) – равномерное распределение (a и b –
граничные точки интервала,
причем a < b и a
x
b);
dweibull(x, s) – распределение Вейбулла (s > 0 – параметр формы).
Функции распределения дают вероятность того, что случайная величина будет
иметь значения, меньшие или равные определенной величине. Они представлены
аналогичным набором функций и отличаются от приведенных тем, что первой
буквой имени является буква p, а не d (например, pbeta(x, s1, s2) и т.д.). При
экстраполяции используются отрезки прямых, проведенных через две крайние
точки. Следующая группа задает обращения (квантили) функций распределения
случайных величин. Они начинаются с буквы q – qbeta(p, s1, s2) и т.д. и позволяют
по заданной вероятности вычислить такое значение x, при котором вероятность
равна или меньше заданного значения p.
Последняя группа статистических функций служит для создания векторов с
определенными законами распределения значений их элементов. Они
начинаются с буквы r – например rbeta(m, s1, s2) и т.д.
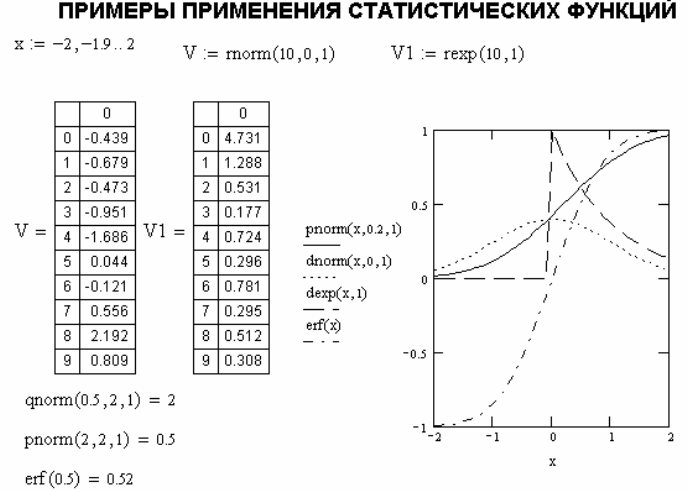
Примеры применения некоторых статистических функций и построения их
графиков даны на рисунке A.18.
Рисунок A.18 – Примеры применения статистических функций
A.7.3 Выполнение регрессии разного вида
Другой широко распространенной задачей обработки данных является
представление их совокупности некоторой функцией y(x). Задача регрессии
заключается в получении параметров этой функции такими, чтобы функция
приближала бы облако исходных точек (заданных векторами VX и VY) с
наименьшей среднеквадратичной погрешностью.
372
Чаще всего используется линейная регрессия, при которой функция y(x) имеет
вид y(x) = a + b
x и описывает отрезок прямой. К линейной регрессии можно
свести многие виды нелинейной регрессии при зависимостях вида y(x).
Для проведения линейной регрессии в систему встроен ряд приведенных ниже
функций:
corr(VX, VY) – возвращает скаляр – коэффициент корреляции Пирсона;
intercrpt(VX, VY) – возвращает значение параметра а (смещение линии регрессии
по вертикали);
slope(VX, VY) – возвращает значение параметра b (угловой коэффициент линии
регрессии).
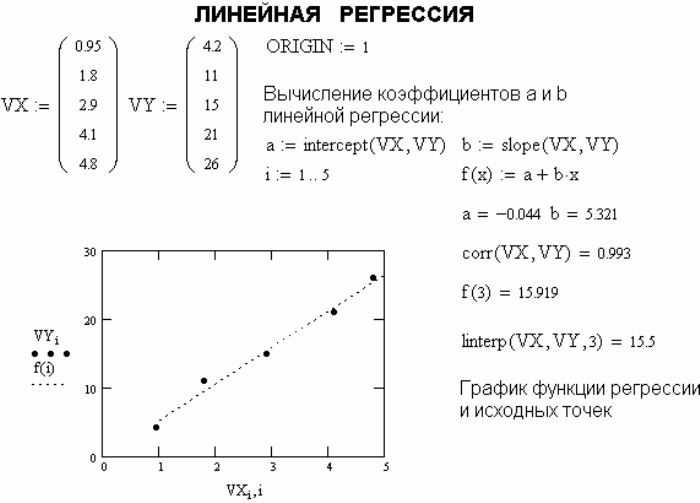
Как видно на рисунке A.19, прямая регрессии проходит в «облаке» исходных точек
с максимальным среднеквадратичным приближением к ним. Чем ближе
коэффициент корреляции к 1, тем точнее представленная исходными точками
зависимость приближается к линейной.
Рисунок A.19 – Пример линейной регрессии
В Mathcad реализована возможность выполнения линейной регрессии общего
вида. При ней заданная совокупность точек приближается функцией вида:
F(x,K
1
,K
2
,...,K
n
)=K
1
F
1
(x)+K
2
F
2
(x)+...+K
n
F
n
(x).
Таким образом, функция регрессии является линейной комбинацией функций
F
1
(x), F
2
(x),...,F
n
(x), причем сами эти функции могут быть нелинейными. Для
реализации линейной регрессии общего вида используется функция linfit(VX, VY,
F). Она возвращает вектор коэффициентов линейной регрессии общего вида K,
при котором среднеквадратичная погрешность приближения «облака» исходных
точек, координаты которых хранятся в векторах VX и VY, оказывается
минимальной. Вектор F должен содержать функции F
1
(x), F
2
(x),..., F
n
(x),
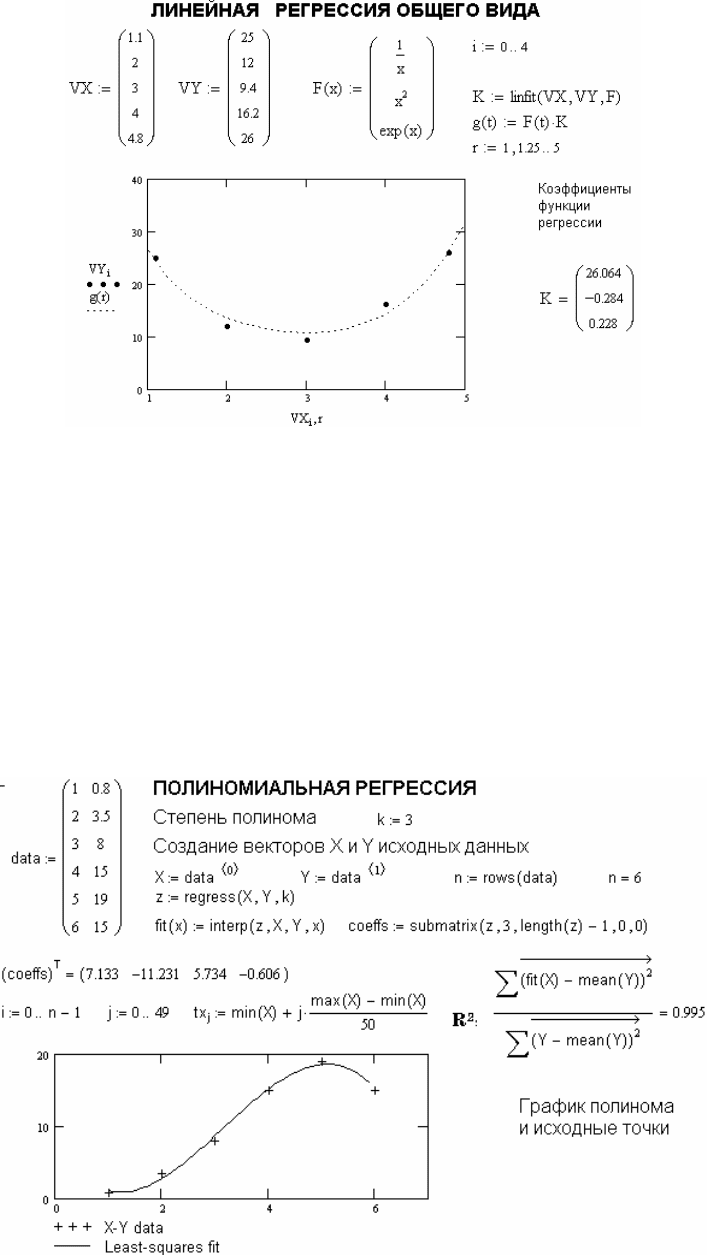
записанные в символьном виде (пример показан на рисунке A.20). Вектор VX
должен содержать координаты, упорядоченные в порядке их возрастания, а
вектор VY содержать ординаты, соответствующие абсциссам в векторе VX.
373
Рисунок A.20 – Пример проведения линейной регрессии общего вида
В Mathcad введена и функция для обеспечения полиномиальной регрессии при
произвольной степени полинома регрессии: regress(VX,VY,n). Она возвращает
вектор VS, запрашиваемый функцией interp(VS,VX,VY,x), содержащий
коэффициенты многочлена n-й степени, который наилучшим образом приближает
«облако» точек с координатами, хранящимися в векторах VX и VY – рисунок A.21.
Для вычисления коэффициентов полинома регрессии используется функция
submatrix. На практике не рекомендуется делать степень аппроксимирующего
полинома выше 4-6, поскольку погрешности реализации регрессии сильно
возрастают.
Рисунок A.21 – Полиномиальная регрессия
Функция regress создает единственный приближающий полином, коэффициенты
которого вычисляются по всей совокупности заданных точек. Иногда полезна
другая функция полиномиальной регрессии, дающая локальные приближения
отрезками полиномов второй степени: loess(VX, VY, span) – возвращает вектор
374
VS, используемый interp(VS,VX,VY,x) для наилучшего приближения данных VX и
VY отрезками полиномов второй степени. Аргумент span>0 указывает размер
локальной области приближаемых данных (рекомендуемое начальное значение –
0.75). Чем больше span, тем сильнее сказывается сглаживание данных. При
больших span эта функция приближается к regress(VX,VY,2). Mathcad
8.0/2000/2001 PRO с помощью этих функций позволяет выполнять также
многомерную регрессию.
Под нелинейной регрессией общего вида подразумевается нахождение вектора K
параметров произвольной функции F(x,K1,K2,...,Kn), при котором обеспечивается
минимальная среднеквадратичная погрешность приближения «облака» исходных
точек. Для проведения нелинейной регрессии общего вида используется функция
genfit(VX, VY, VS, F). Она возвращает вектор K параметров функции F, дающий
минимальную среднеквадратичную погрешность приближения функцией
F(x,K1,K2,...,Kn) исходных данных. F должен быть вектором с символьными
элементами, причем они должны содержать аналитические выражения для
исходной функции и ее производных по всем параметрам. Вектор VS должен
содержать начальные значения элементов вектора K, необходимые для решения
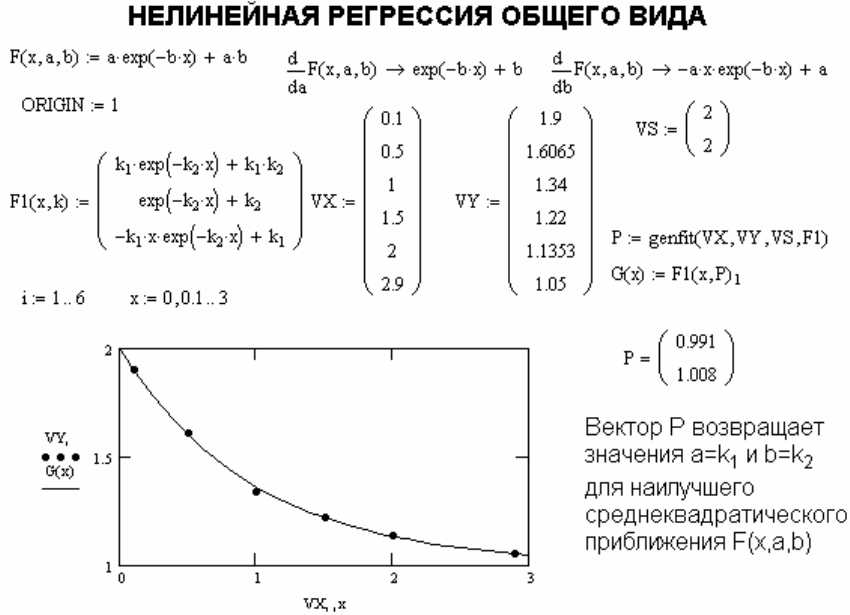
системы нелинейных уравнений регрессии итерационным методом. На рисунке
A.22 показан пример выполнения нелинейной регрессии общего вида с помощью
нелинейной функции F(x,a,b)=aexp(–b
x)+a
b.
Рисунок A.22 – Пример выполнения нелинейной регрессии общего вида
При решении этой задачи возникают две проблемы. Во-первых, надо вычислить
значения производных по переменным a и b. В документе на рисунке A.22 это
сделано с помощью символьных операций (первая строка документа после
заголовка), что наглядно показывает пользу от таких операций. Вторая проблема
связана с необходимостью применения функции genfit в ее стандартном виде.
Поэтому пришлось заменить параметр a на k
1
, а параметр b на k
2
.
375
A.7.4 Новые функции Mathcad для проведения регрессии
Начиная с версии Mathcad 2000 PRO в систему Mathcad был введен ряд новых
функций регрессии:
expfit(vx, vy, vg) – возвращает вектор, содержащий коэффициенты (a, b и c)
аппроксимирующего выражения вида a
e
(b
x)+c
, которое лучшим образом
приближается к точкам, координаты которых хранятся в векторах vx и vy (вектор
vg содержит первое приближение к решению).
lgsfit(vx, vy, vg) – тоже для выражения a/(1+b
e
(-c
x)
).
logfit(vx, vy) – тоже для выражения a
ln(x+b)+c (начального приближения не
требуется).
medfit(vx, vy) – тоже для выражения a+b
x (начального приближения не требуется).
pwrfit(vx, vy, vg) – тоже для выражения a
x
b
+c. Вектор vg содержит первое
приближение к решению.
sinfit(vx, vy, vg) – тоже для выражения a
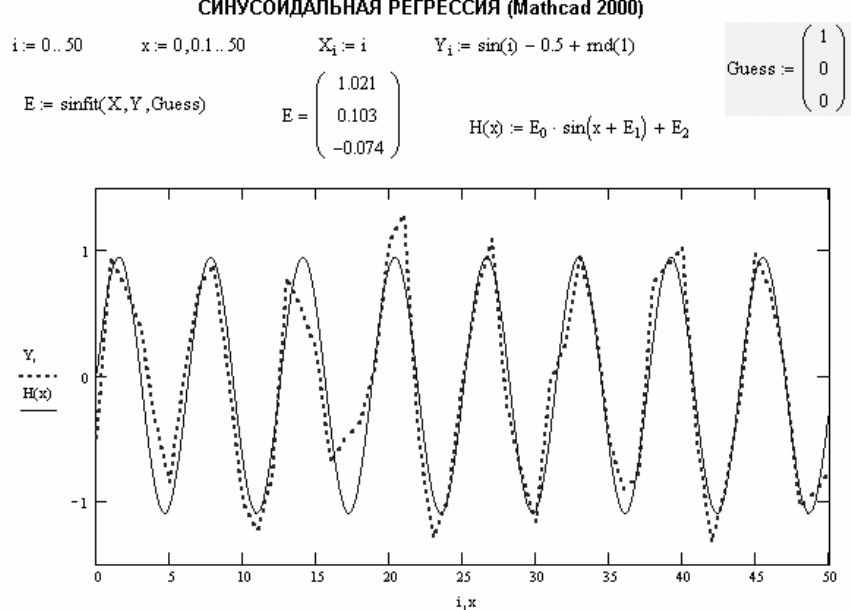
sin(x+b)+c (рисунок A.17).
Рисунок A.23 – Пример синусоидальной регрессии
В примере рисунок A.23 реализована регрессия реализуется функцией sinfit.
Подобным образом можно реализовать и другие варианты регрессии.
A.7.5 Функции сглаживания и предсказания
Данные большинства экспериментов имеют случайные составляющие. Поэтому
часто возникает необходимость статистического сглаживания данных. Ряд
функций Mathcad предназначен для выполнения операций сглаживания данных
различными методами. В их названии имеется слово smooth (гладкий):
medsmooth(VY,n), ksmooth(VX, VY, b) и supsmooth(VX, VY). Они реализуют
376
соответственно метод скользящей медианы, сглаживания окном Гаусса и
адаптивного сглаживания. Параметры n и b задают ширину окна сглаживания. На
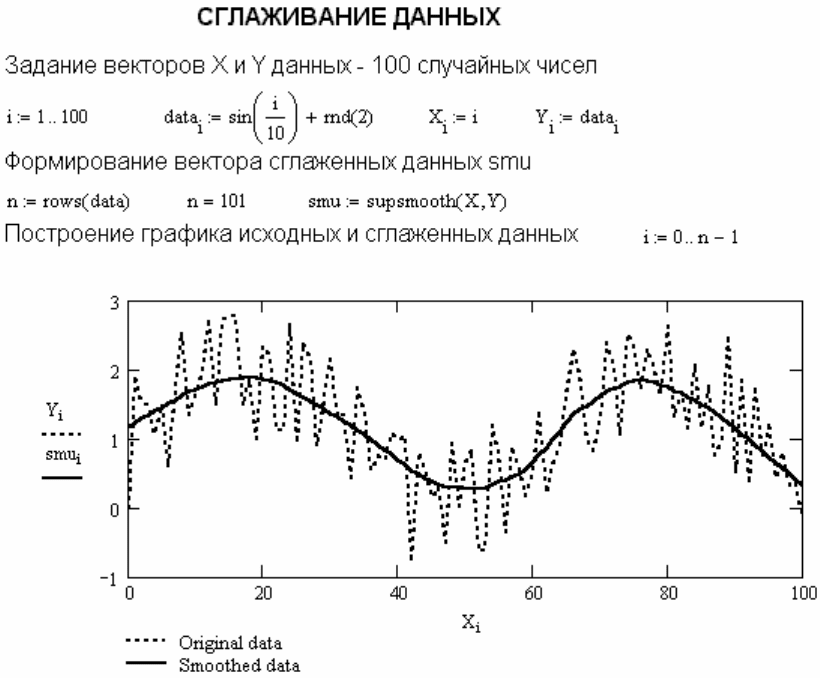
рисунке A.24 показан пример применения функции subsmooth(X,Y). Здесь вектор
данных формируется из синусоиды, на которую наложены случайные числа,
которые генерируются вфункцией rnd.
Рисунок A.24 – Сглаживание вектора данных
Для предсказания поведения некоторой зависимости служит функция
prediсt(data,m,N),
где data – вектор данных,
m – число точек с конца этого вектора, используемых для окна предсказания,
N – число точек. Она, по ряду заданных равномерно расположенных точек,
позволяет рассчитать некоторое число N последующих точек, т. е., по существу,
осуществляет экстраполяцию произвольной (но достаточно гладкой и
предсказуемой) зависимости – рисунок A.25. Эта функция реализует метод Бурга,
описанный в 1992 году, который относится к авторегрессионным методам
предсказания.
377
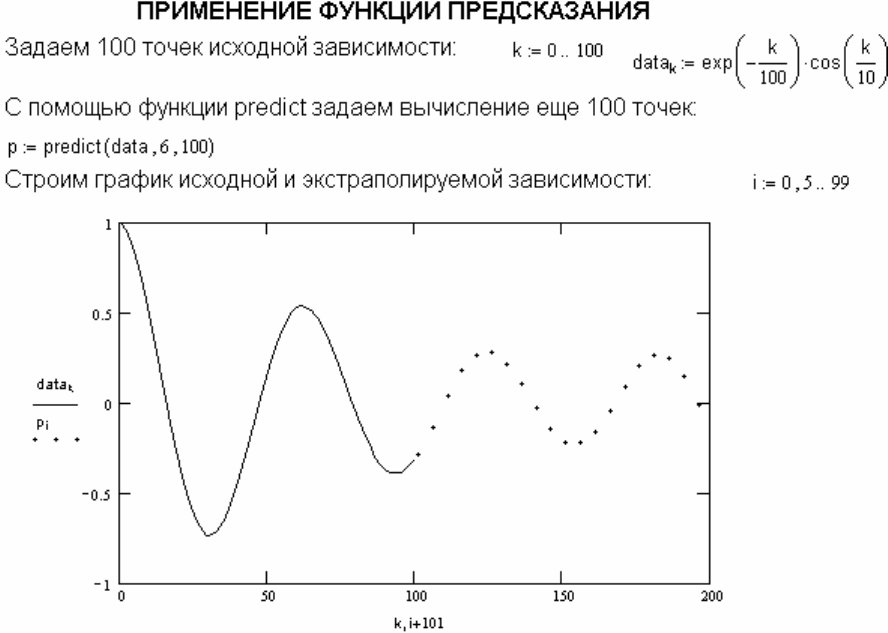
Рисунок A.25 – Применение функции предсказания – экстраполяции
Функция предсказания обеспечивает высокую точность при монотонных исходных
функциях или функциях, представляемых полиномами невысокой степени. Но
рисунок A.19 показывает, что она неплохо предсказывает и функции, содержащие
явную колебательную компоненту. Подстройкой m и применением
предварительного сглаживания можно добиться неплохих успехов в предсказании
даже сильно зашумленных зависимостей. Если вектор исходных данных содержит
неравномерно распределенные отсчеты, то хорошие результаты дает
предварительная сплайновая интерполяция, из которой затем можно
сформировать вектор отсчетов с равномерным распределением.
A.8 Решение нелинейных уравнений и систем
A.8.1 Функция поиска корня нелинейного уравнения root
Многие уравнения, например трансцендентные, и системы из них не имеют
аналитических решений. Однако они могут решаться численными методами с
заданной погрешностью (не более значения, заданного системной переменной
TOL). Для простейших уравнений вида F(x)=0 решение находится с помощью
функции root(Выражение, Имя_переменной[,a,b]). Эта функция возвращает
значение переменной, при котором выражение равно 0 с заданной точностью.
Функция реализует вычисления итерационным методом, причем можно задать
начальное значение переменной. Примеры показаны ниже:
x 10
root x
2
x 21 x
4.11
x 10
root x
2
x 21 x
5.11

378
Можно также (только в Mathcad 2000/2001) задать интервал от a до b поиска корня
– примеры на рисунке A.13, где ищутся корни функции, заданной как функция
пользователя. Возможно решение систем нелинейных уравнений – в этом случае
параметры функции надо задавать в векторной форме.
A.8.2 Функция поиска всех корней многочлена polyroots
Для поиска корней обычного полинома p(x) степени n Mathcad содержит очень
удобную функцию polyroots(V). Она возвращает вектор всех корней многочлена
(полинома) степени n, коэффициенты которого находятся в векторе V, имеющим
длину равную n+1. Пример:
Здесь найдены корни многочлена 4-ой степени. Из них два корня действительные,
два другие комплексно-сопряженные.
A.8.3 Директива Given для подготовки блока решения системы уравнений
При решении систем нелинейных уравнений используется специальный
вычислительный блок, открываемый служебным словом - директивой Given, и
имеющий следующую структуру:
Начальные условия (вида var := value)
Given
Уравнения (вида expr_left = expr_right)
Ограничительные условия (вида x>0 и т.д.)
Выражения с функциями Find, Minerr, Maximize и Minimize
Возможно задание уравнений и ограничительных условий в векторной форме.
A.8.4. Функции Find и Minerr для решения систем нелинейных уравнений
В блоке используется одна из следующих двух функций:
Find(v1, v2, ..., vn) – возвращает значение одной или ряда переменных для
точного решения и Minerr(v1, v2, ..., vn) – возвращает значение одной или ряда
переменных для приближенного решения методом наименьших квадратов.
Рисунок A.26 иллюстрирует решение задачи на поиск точек пересечения
параболы и прямой. В нашем случае с помощью функции Find решается система
из двух уравнений (одно из них нелинейное) с ограничительными условиями,
задающими область поиска корня (x < 0 для отрицательного корня и x > 0 для
положительного корня).
V 2 6 3 4 1( )
T
polyroots V( )
3.587
0.371
0.021 1.225i
0.021 1.225i

379
Рисунок A.26 – Вычисление координат точек пересечения параболы прямой
При использовании функции Minerr для решения систем нелинейных уравнений
надо проявлять известную осторожность и обязательно предусматривать
проверку решений. Нередки случаи, когда решения могут оказаться ошибочными,
чаще всего из-за того, что из нескольких корней система предлагает нереальный
(или не представляющий интереса) корень. Полезно как можно точнее указывать
начальные приближения к решению.
A.9 Реализация итерационных вычислений
Система Mathcad позволяет реализовать вычисления, осуществляемые
итерационным соотношениям – это когда значение некоторой функции находится
по одному или нескольким предшествующим ее значениям. Пример показан ниже
на числа Фибоначчи.
Как известно, два первых числа Фибоначчи определены как 1, а последующие
есть сумма двух предыдущих. Результат задан как вектор-строка чисел
Фибоначчи.
Более актуальна задача реализации вычислений, в том числе итерационных, с их
окончанием по некоторому заданному условию. Для этого система Mathcad
содержит специальную функцию until (Выражение_1, Выражение_2). Она
позволяет повторять вычисления с возвратом значения выражения 2, до тех пор
пока выражение 1 больше или равно 0. В противном случае вычисления
прекращаются. Ниже показано действие этой функции на другом классическом
ORIGIN
1
x
1
1
i
3
10
x
i
x
i 2( )
x
i 1( )
x
T
1 2 3 4 5 6 7 8 9 10
1 1 0 1 1 2 3 5 8 13 21
380
примере – вычислении квадратного корня из числа a итерационным методом
Ньютона:
i
0
12
q
0
1
err .01
a 64
q
i 1
until q
i
2
a
err
q
i
a
q
i
2
q
T
1 32.5 17.235 10.474 8.292 8.005 8 0( )
Этот пример позволяет наглядно проследить динамику схождения к точному
результату результатов вычислений по итерационной формуле Ньютона.
Применение итерационных вычислений зачастую позволяет нагляжно
представить довольно сложные физико-химические явления. Примером может
служить имитация броуновского случайного движения частиц. Для этого
достаточно на каждом шаге итераций просто прибавлять случайные координаты x
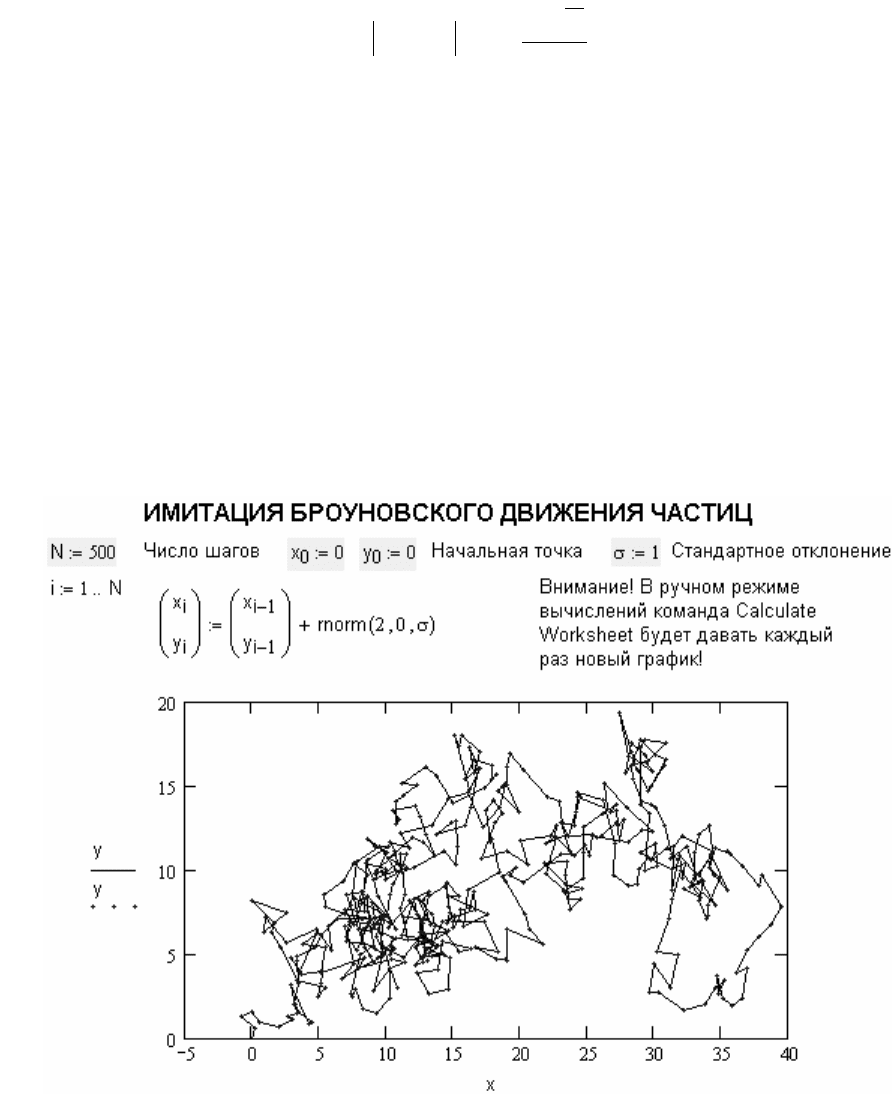
и y для положения частицы, движение которой имитируется. Рисунок A.27
показывает документ Mathcad в котором такая имитация дана для случая
движения частицы в плоскости. Следует отметить, что из за случайности задания
координат вид рисунка будет меняться при каждом пуске этого документа.
Рисунок A.27 – Имитация броуновского движения частицы в плоскости
В общем случае итерационные вычисления могут осуществляться по нескольким
формулам, причем возможно перекрестное применение в них переменных. Такого
рода вычисления в системе Mathcad необходимо реализовать в векторной форме
– рисунок A.28. В этом случае уточнение значений переменных идет не по
строкам, а по столбцам.
