Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.

381
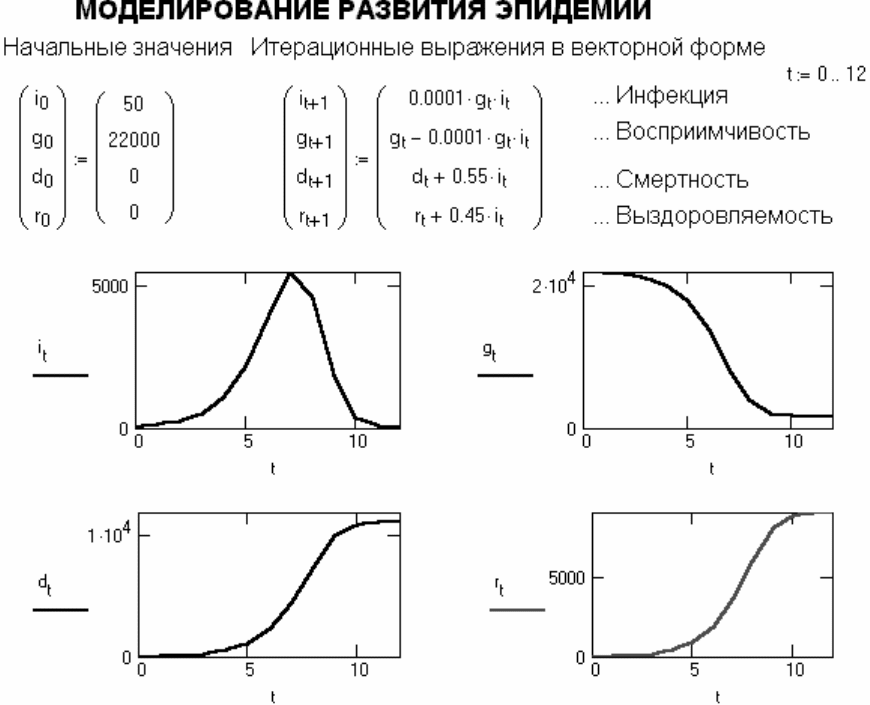
Рисунок A.28 – Динамика протекания процесса эпидемии (параметр p
характеризует меры профилактики)
Возможны и более сложные реализации итерационных, рекуррентных и других
подобных вычислений. Например, к ним сводится решение систем
дифференциальных уравнений любыми разностными методами, например,
Эйлера, Рунге – Кутта и др.
A.10 Решение задач оптимизации и линейного программирования
Решение задач оптимизации - одна из важнейших сфер применения
математических методов. Такое решение легко дается с помощью функции Minerr,
однако в Mathcad 2000/2001 имеются специальные функции для решения задач
оптимизации и оинейного программирования. Так, для поиска значений
переменных x1, x2,...,xn, при которых некоторая функция f(x1, x2,...,xn) имеет
максимальное или минимальное значения используются функции maximize(f,x1,
x2,...,xn) и minimize(f,x1, x2,...,xn). Обе эти функции реализованы достаточно
универсальными алгоритмами оптимизации, которые не требуют вычисления
производных функции f(x1, x2,...,xn), что не только упрощает запись алгоритмов,
но и позволяет решать задачи, в которых вычисление производных по тем или
иным причинам невозможно.
Ниже дан пример на поиск минимума и максимума с применением функций
Maximize и Minimize. В данном случае ищется минимум хорошо известной
тестовой функции Розенброка.

382
f x y( ) 100 y x
2
2
1 x( )
2
x 0 y 0
Given
P Minimize f x y( )
P
1
1
f P
0
P
1
2.004 10
10
Given
x 0 y 0 y 9 x
R Maximize f x y( ) R
0
0
f R
0
R
1
1
Функции Maximize и Minimize могут успешно применяться при решении задач
линейного программирования, которые широко используются в экономических и
производственных расчетах. На рисунке A.29 представлен пример решения такой
конкретной задачи с соответствующим описанием ее постановки. Решается
довольно актуальная для химического производства и практики применения
горючих материалов задача подготовки смеси веществ (бензина с минимальной
стоимостью).
Рисунок A.29 – Пример решения задачи линейного программирования
Приведенные примеры показывают, что введение в Mathcad 8/2000 новых
функций оптимизации Maximize и Minimize расширяет круг решаемых системой
задач при минимальных затратах времени на подготовку средств их решения.
383
A.11 Решение дифференциальных уравнений
A.11.1 Функции для решения ДУ различного вида
Многие задачи (особенно динамические) в области математики, физики и химии
сводятся к решению систем дифференциальных уравнений - как линейных, так и
нелинейных. Для численного решения обыкновенных дифференциальных
уравнений (ОДУ) в Mathcad введены следующие функции:
rkadapt(y, x1, x2, acc, n, F, k, s) – возвращает матрицу решения на интервале от x1
до x2 для системы ОДУ, вычисленную методом Рунге-Кутта с переменным шагом
и начальными условиями в векторе y (правые части системы записаны в векторе
F, n – число шагов, k – максимальное число промежуточных точек решения и s –
минимально допустимый интервал между точками);
Rkadapt(y, x1, x2, n, F) – возвращает матрицу решений методом Рунге-Кутта с
переменным шагом для системы ОДУ с начальными условиями в векторе y,
правые части которых записаны в символьном векторе F, на интервале от x1 до
x2; n – число шагов;
rkfixed(y, x1, x2, n, F) – возвращает матрицу решений методом Рунге-Кутта
системы обыкновенных ОДУ с начальными условиями в векторе y, правые части
которых записаны в символьном векторе F, на интервале от x1 до x2 при
фиксированном числе шагов n.
Рисунок A.30 иллюстрирует технику решения системы из двух
дифференциальных уравнений Ван-дер-Поля и представление решения в виде
фазового портрета колебаний, которые описывает рассматриваемая система
уравнений, а также временных зависимостей решения. Эта система описывает
типичную нелинейную систему второго порядка. Степень нелинейности задается
параметром, в зависимости от значения которого можно получить затухающие,
стационарные или нарастающие по амплитуде колебания. Отличие фазового
портрета от эллипса указывает на степень нелинейности системы.
384
Рис. A.30 – Решение системы дифференциальных уравнений с применением
функции rkfixed
Если решение системы дифференциальных уравнений имеет вид гладких
функций, то вместо функции rkfixed, описанной ранее, целесообразно применять
функцию Bulstoer(y, x1, x2, n, F), реализующую метод Булирша—Штера.
Система дифференциальных уравнений, записанная в матричной форме y = A
x,
где A – почти вырожденная матрица, называется жесткой. Для решения систем
жестких дифференциальных уравнений в последние версии Mathcad введен ряд
функций: bulstoer(y, x1, x2, acc, n, F, k, s), Stiffb(y, x1, x2, n, F, J), stiffb(y, x1, x2, acc,
n, F, J, k, s), Stiffr(y, x1, x2, n, F, J) и stiffr(y, x1, x2, acc, n, F, J, k, s). Они
возвращают матрицу решения в интервале от x2 до x2, векторе начальных
условий y и других, отмеченных выше параметров. Используется метод Булириш-
Штера и Розенброка (последний требует определения Якобиана J). В
приведенных функциях:
acc – погрешность решения (рекомендуется порядка 0.001),
k – максимальное число промежуточных точек,
s – минимально-допустимый интервал между точками, в которых ищется решение.
Функции, начинающиеся с малой буквы, дают решения только для конечной точки.
Пример решения жесткой системы дифференциальных уравнений дан на рисунке
A.31.
385
Рисунок A.31 – Пример решение жесткой системы из двух дифференциальных
уравнений
Для решения дифференциальных уравнений Пуассона (в частных производных
второго порядка) и уравнений Лапласа в систему введены следующие функции:
multigrid(M, n) – возвращает матрицу решения уравнения Пуассона, у которого
решение равно нулю на границах и relax(M1, M2, M3, M4, M5, A, U, r) –
возвращает квадратную матрицу решения уравнения Пуассона для спектрального
радиуса r; Для решения двухточечных краевых задач предназначены функции:
bvalfit и sbval.
A.11.2 Функция odesolve
Для унификации решения одиночных дифференциальных уравнений в составе
блока решения Given в Mathcad 2000 PRO была введена новая функция
odesolve(x,b[,steps]). Она возвращает вектор решения ОДУ при заданных
начальных условиях и конце интервала интегрирования b. Если указано число
шагов steps, то решение выполняется с фиксированным шагом, иначе - решение
выполнятся адаптивным методом. Хотя аналитическое выражение для этой
функции не выводится с ней можно выполнять математические преобразования,
например, дифференцировать – рисунок A.32.
386
Рисунок A.32 – Решение дифференциального уравнения второго порядка с
помощью функции odesolve
В этом примере решение дифференциальных уравнений выглядит более логично
и привычно - также, как и в блоках, решающих нелинейные уравнения. Множество
примеров решения дифференциальных уравнений читатель найдет в
последующих главах книги
A.12 Символьные вычисления и оптимизация
Весьма важной возможностью Mathcad является способность выполнять
символьные (аналитические) вычисления. Лучше всего для этого использовать
специальный оператор вывода символьных результатов и палитру символьных
операций (кнопка с академической шапочкой). Выполняемые операции
перечислены ниже (знаком отмечены операции, имеющиеся только в
профессиональных версия).
Simplify
Упрощение выражений
expand
Разложение выражения по степеням
factor
Разложение выражения на простые дроби
complex
Преобразования в комплексной форме
assume
Придание переменным заданных свойств и ограничений
series
Разложение в ряд по заданным переменным
float
Преобразование в формат чисел с плавающей точкой
parfac Разложение на элементарные дроби
coeffs Возвращает коэффициенты полинома

387
fourier Прямое преобразование Фурье
laplace Прямое преобразование Лапласа
ztrans
Прямое z – преобразование
invfourier Обратное преобразование Фурье
invlaplace Обратное преобразование Лапласа
invztrans
Обратное z –преобразование
M
T
Транспонирование матрицы
M
-1
Инвертирование матрицы
|M|
Вычисление детерминанта матрицы
Modifier
Модифицированные команды:
assume – вводное слово для приведенных ниже
определений;
real – для var = real означает вещественное значение var;
RealRange – для var = RealRange(a,b) означает
принадлежность вещественной var к интервалу [a,b];
trig – задает направление тригонометрических
преобразований.
Большую часть из этих операций можно выполнять и в командном режиме,
используя команды, входящие в позицию Symbolics главного меню. Последняя
команда в этой позиции Evalution Style... выводит окно установки стиля вывода:
снизу исходного выражения (с пустой строкой и без нее), справа от исходного
выражения, на его месте и с комментарием или без него. Примеры символьных
операций в командном режиме (дифференцирование, интегрирование и
разложение в ряд Тейлора) представлены ниже:
Полезно обратить внимание на то, что часть операций выполняется над
выделенным выражением, а часть над выделенной переменной. В командном
режиме символьных вычислений нельзя преобразовывать выражения,
содержащие функции пользователя. Однако, при использовании оператора
символьного вывода это возможно. Ниже представлены типовые операции
символьной математики на вычисление производной, интеграла, синуса кратных
углов, решение квадратного уравнения и осуществление подстановки:
f x n( ) x
n
x
f x n( )
d
d
x
n
n
x
xf x n( )
d
x
n 1
n 1
Differentiate Integrate Expand to series...
sin x( )
x
n
x
n
by integration, yields converts to the series
x
n n
x
x
n 1( )
n 1( )
1 x
1
6
x
3
1
120
x
5
O x
6
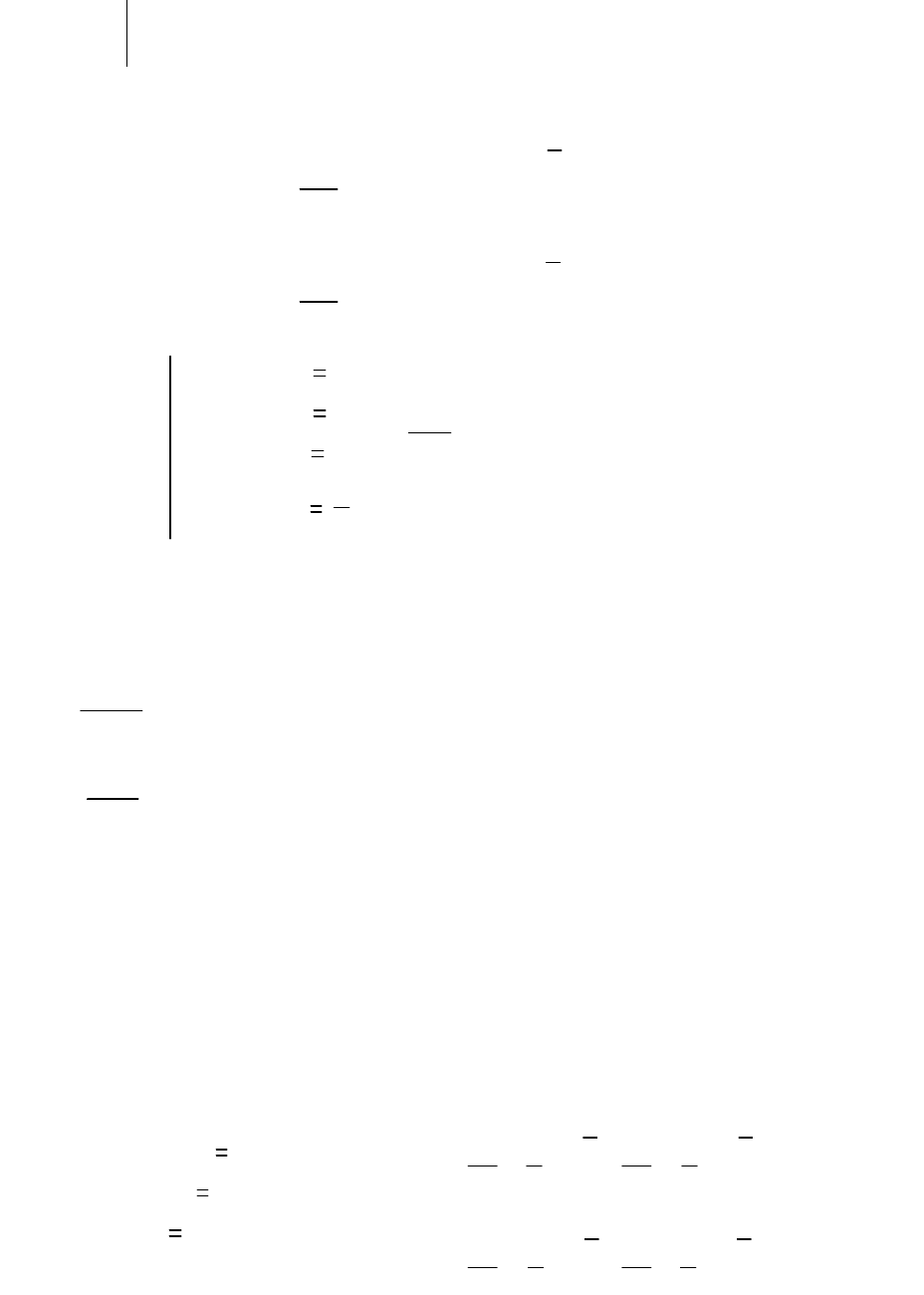
388
sin 5 x( )( )
trig
expand x
16 sin x( ) cos x( )
4
12 sin x( ) cos x( )
2
sin x( )
a x
2
b x c solve x
1
2 a
b b
2
4 a c
1
2
1
2 a
b b
2
4 a c
1
2
a x
2
b x c
substitute a 5
substitute b 10
substitute c 20
substitute x
1
3
215
9
Нетрудно заметить возможность комбинирования символьных операций и их
объединений вертикальной чертой. Возможно символьное вычисление пределов
функций:
f x( )
sin x( )
x
x
1x
f x( )lim
sin 1( )
2x
g x( )lim
g x( )
1
x 2
2
x
g x( )lim
Более подробно о применении символьных операций вы прочтете в главе,
посвященной системе символьной математики Maple V (ядро этой системы
использовано для проведения символьных вычислений в Mathcad). Здесь же
приведем эффектный прием применения символьных операций - решение в
аналитическом виде системы нелинейных уравнений, заданных в векторной
форме:
x
2
y
2
z
2
3
x y z 1
x y 1
solve x y z
1
1
2
1
2
i 3
1
2
1
2
1
2
i 3
1
2
1
1
2
1
2
i 3
1
2
1
2
1
2
i 3
1
2
1
2
2
Mathcad имеет весьма полезное средство оптимизации вычислений. Его суть
заключается в получении аналитическое представление вычисляемого
выражения - например интеграла, производной и т.д. После этого вычисления
выполняются уже не медленными численными методами, а быстро по
аналитическим выражениям. Оптимизация включается опцией Optimization в
389
позиции Math главного меню. Оптимизируемые выражения помечаются красной
звездочкой (*).
A.13 Программирование в системе Mathcad
A.13.1 Основные средства программирования
Как уже отмечалось, Mathcad по существу является системой визуального
программирования. Однако, есть и палитра со средствами обычного
программирования:
Add Line
Cоздает и при необходимости расширяет жирную вертикальную
линию, справа от которой в шаблонах задается запись
программного блока
Локальное присваивание в теле модуля программы
if
Создание условного выражения
for
Задание цикла с фиксированным числом повторений
while
Задание цикла типа "пока"
otherwise Иной выбор (обычно применяется с оператором if)
break
Прерывание
continue
Продолжение
return
Возврат
on error
Обработка ошибок
Оператор выполняет функции внутреннего, локального присваивания. Пример
его применения для задания программного модуля – функции пользователя дан
ниже:
FP x y z( ) a x y z
x y z
a
FP 2 3 5( ) 0.588 FP 1 5 3( ) 0.563
Оператор if является оператором для создания условных выражений:
Выражение if Условие
Если Условие выполняется, то возвращается значение Выражения.
Пример
abs x( ) x x 0if
x otherwise
abs 5( ) 5 abs 5( ) 5
Применение оператора цикла for для вычисления суммы и
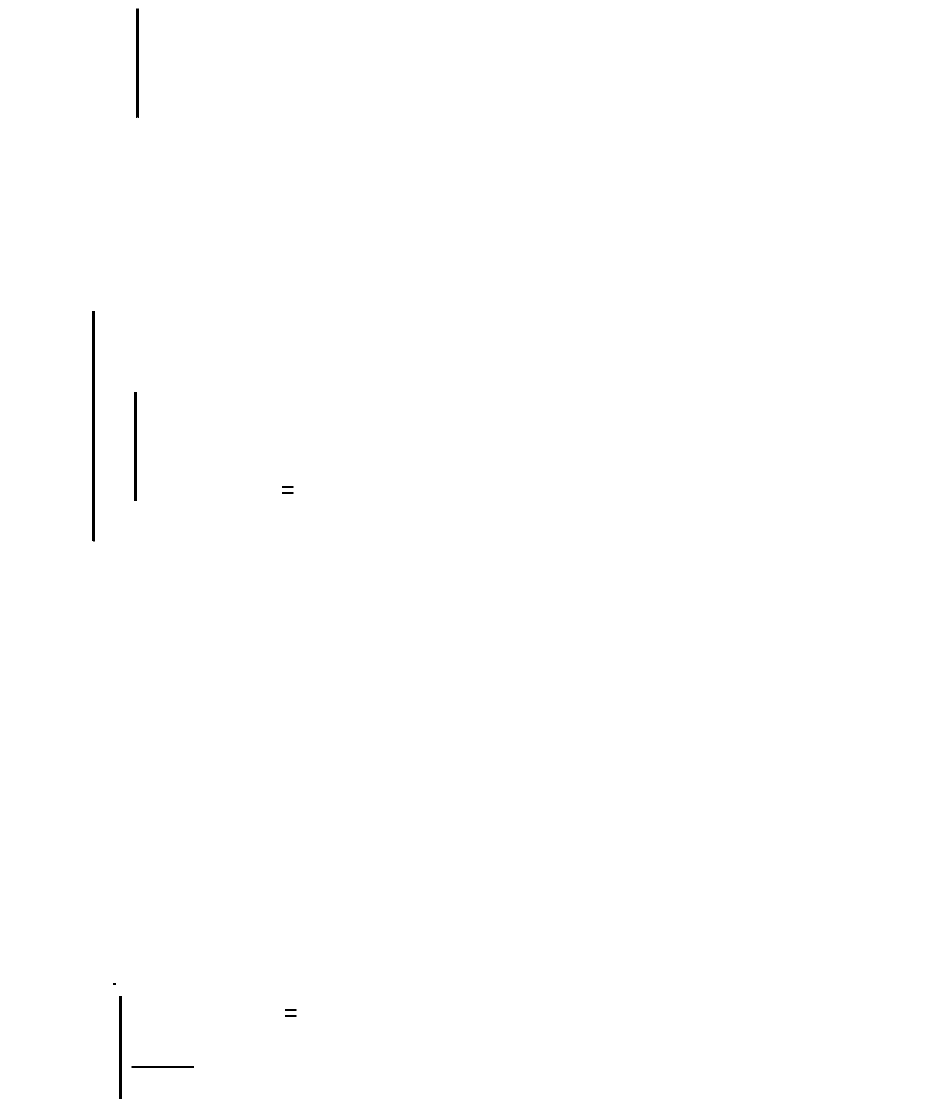
390
Совместно с этим оператором часто используются операторы прерывания break и
оператор иного выбора otherwise. Оператор for служит для организации циклов с
заданным числом повторений выражений, помещаемых в шаблон:
for Var
Nmin .. Nmax
Ниже дан пример вычисления суммы n членов натурального ряда чисел с
применением оператора for:
sum n( ) s 0
s s i
i 1 nfor
sum 10( ) 55
sum 20( ) 210
Оператор while служит для организации циклов, действующих до тех пор, пока
выполняется некоторое условие:
while Условие
Ниже представлен учебный пример на задание функции вычисления факториала
F(n) с применением двухступенчатого программного модуля с циклом while:
F n( ) f n
f f n 1( )
n n 1
break n 1if
1while
f
F 10( ) 3.629 10
6
F 3( ) 6
Оператор иного выбора otherwise обычно используется совместно с оператором if.
Это поясняет следующая программная конструкция:
f(x) := 1 if x>0 возвращает 1 если x > 0
-1 otherwise возвращает -1 во всех иных случаях
Оператор продолжения используется для продолжения работы после прерывания
программы. Он также чаще всего используется совместно с операторами задания
циклов while и for, обеспечивая возврат в точку прерывания и продолжение
вычислений. Особый оператор return прерывает выполнение программы и
возвращает значение своего операнда, стоящего следом за ним. Например, в
выражении return 0 if x<0 будет возвращаться значение 0 при любом x < 0. В
представленном ниже примере оператор return используется для вычисления
sin(x)/x в особой точке x=0:
error
"No value!!!"
(
)
otherwise
S x( ) 1return x 0if
sin x( )
x
otherwise
S 0( ) 1 S 1( ) 0.841 S 1( ) 0.841
Оператор обработки ошибок позволяет создавать конструкции обработчиков
ошибок:
Выражение_1 on error Выражение_2
