Hjorth-Jensen M. Computational Physics

Подождите немного. Документ загружается.

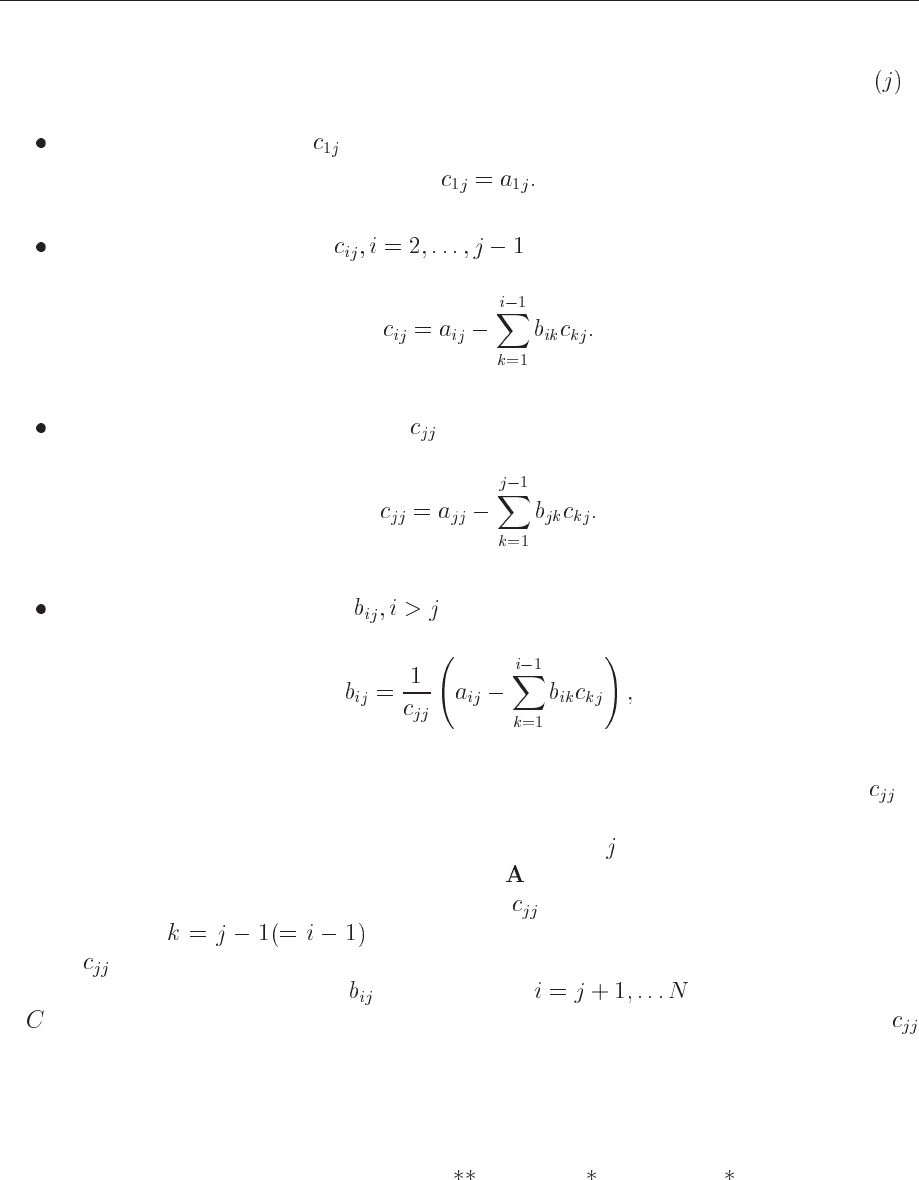
5.3. LU DECOMPOSITION OF A MATRIX 79

which gives the following algorithm:

Calculate the elements in B and C columnwise starting with column one. For each column

Compute the ﬁrst element by

(5.6)

Next, Calculate all elements

(5.7)

Then calculate the diagonal element

(5.8)

Finally, calculate the elements

(5.9)

The algorithm is known as Crout’s algoithm. A crucial point is obviously the case where is

close or equals to zero which can lead to signiﬁcant loss of precision. The solution is pivoting

(interchanging rows ) around the largest element in a column . Then we are actually decom-

posing a rowwise permutation of the original matrix

. The key point to notice is that eqs. (5.8,

5.9) are equal except for the case that we divide by in the latter one. The upper limits are

always the same

. This means that we do not have to choose the diagonal

element as the one which happens to fall along the diagonal in the ﬁrst instance. Rather, we

could promote one of the undivided ’s in the column to become the diagonal

. The partial pivoting in Crout’s method means then that we choose the largest value for

(the pivot element) and then do the divisions by that element. Then we need to keep track of all

permutations performed.

The programs which performs the above described LU decomposition

C: void ludcmp(double

a, int n, int indx, double d)

Fortran: CALL lu_decompose(a, n, indx, d)

are listed in the program libraries:

lib.c

f90lib.f

80 CHAPTER 5. LINEAR ALGEBRA

5.4 Solution of linear systems of equations

With the LU decomposition it is rather simple to solve a system of linear equations

This can be written in matrix form as

where and are known and we have to solve for . Using the LU dcomposition we write

(5.10)

This equation can be calculated in two steps

(5.11)

To show that this is correct we use to the LU decomposition to rewrite our system of linear

equations as

(5.12)

and since the determinat of is equal to 1 (by construction since the diagonals of equal 1) we

can use the inverse of

to obtain

(5.13)

which yields the intermediate step

(5.14)

and multiplying with on both sides we reobtain Eq. (5.11). As soon as we have we can

obtain

through .

For our four-dimentional example this takes the form

(5.15)

and

(5.16)

This example shows the basis for the algorithm needed to solve the set of linear equations. The

algorithm goes as follows

5.5. INVERSE OF A MATRIX AND THE DETERMINANT 81

Set up the matrix A and the vector w with their correct dimensions. This

determines the dimensionality of the unknown vector x.

Then LU decompose the matrix A through a call to the function

C: void ludcmp(double

a, int n, int indx, double d)

Fortran: CALL lu_decompose(a, n, indx, d)

This functions returns the LU decomposed matrix A, its determinant and the

vector indx which keeps track of the number of interchanges of rows. If the

determinant is zero, the solution is malconditioned.

Thereafter you call the function

C: lubksb(double

a, int n, int indx, double w

Fortran: CALL lu_linear_equation(a, n, indx, w)

which uses the LU decomposed matrix A and the vector w and returns x in

the same place as w. Upon exit the original content in w is destroyed. If you

wish to keep this information, you should make a backup of it in your calling

function.

The codes are listed in the program libraries:

lib.c

f90lib.f

5.5 Inverse of a matrix and the determinant

The basic deﬁnition of the determinant of A is

where the sum runs over all permutations of the indices , altogether terms. Also

to calculate the inverse of A is a formidable task. Here we have to calculate

the complementary

cofactor

of each element which is the determinant obtained by striking out the

row

and column in which the element appears. The inverse of A is the constructed as the

transpose a matrix with the elements . This involves a calculation of determinants

using the formula above. Thus a simpliﬁed method is highly needed.

With the LU decomposed matrix A in eq. (5.2) it is rather easy to ﬁnd the determinant

(5.17)

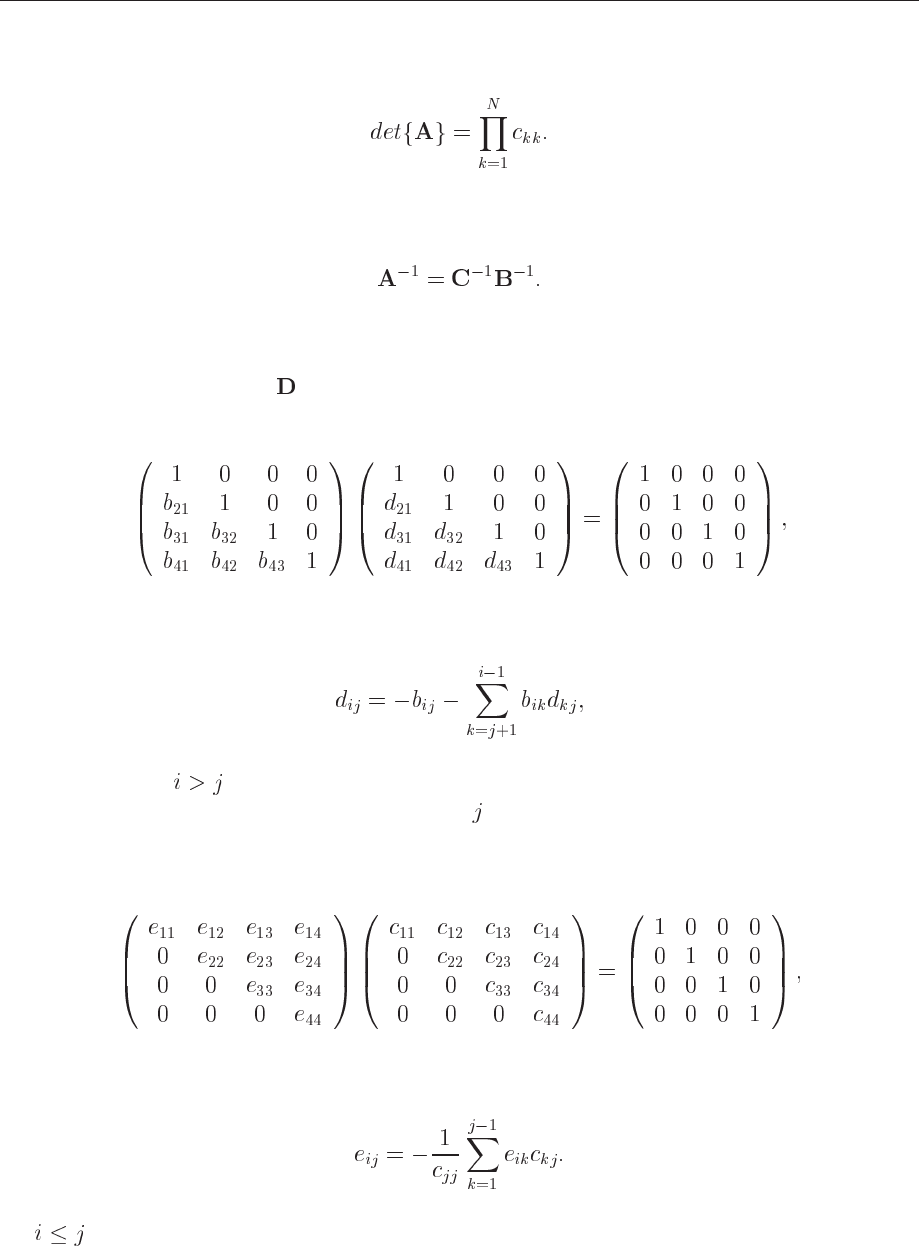
82 CHAPTER 5. LINEAR ALGEBRA

since the diagonal elements of B equal 1. Thus the determinant can be written

(5.18)

The inverse is slightly more difﬁcult to obtain from the LU decomposition. It is formally

deﬁned as

(5.19)

We use this form since the computation of the inverse goes through the inverse of the matrices B

and C. The reason is that the inverse of a lower (upper) triangular matrix is also a lower (upper)

triangular matrix. If we call

for the inverse of B, we can determine the matrix elements of D

through the equation

(5.20)

which gives the following general algorithm

(5.21)

which is valid for . The diagonal is 1 and the upper matrix elements are zero. We solve this

equation column by column (increasing order of ). In a similar way we can deﬁne an equation

which gives us the inverse of the matrix C, labelled E in the equation below. This contains only

non-zero matrix elements in the upper part of the matrix (plus the diagonal ones)

(5.22)

with the following general equation

(5.23)

for

A calculation of the inverse of a matrix could then be implemented in the following way:

5.6. PROJECT: MATRIX OPERATIONS 83

Set up the matrix to be inverted.

Call the LU decomposition function.

Check whether the determinant is zero or not.

Then solve column by column eqs. (5.21, 5.23).

5.6 Project: Matrix operations

The aim of this exercise is to get familiar with various matrix operations, from dynamic memory

allocation to the usage of programs in the library package of the course. For Fortran users

memory handling and most matrix and vector operations are included in the ANSI standard of

Fortran 90/95. For C++ user however, there are three possible options

1. Make your own functions for dynamic memory allocation of a vector and a matrix. Use

then the library package lib.cpp with its header ﬁle lib.hpp for obtaining LU-decomposed

matrices, solve linear equations etc.

2. Use the library package lib.cpp with its header ﬁle lib.hpp which includes a function

for dynamic memory allocation. This program package includes all the other

functions discussed during the lectures for solving systems of linear equations, obatining

the determinant, getting the inverse etc.

3. Finally, we provide on the web-page of the course a library package which uses Blitz++’s

classes for array handling. You could then, since Blitz++ is installed on all machines at the

lab, use these classes for handling arrays.

Your program, whether it is written in C++ or Fortran 90/95, should include dynamic memory

handling of matrices and vectors.

(a) Consider the linear system of equations

This can be written in matrix form as

84 CHAPTER 5. LINEAR ALGEBRA

Use the included programs to solve the system of equations

Use ﬁrst standard Gaussian elimination and compute the result analytically. Compare

thereafter your analytical results with the numerical ones obatined using the programs

in the program library.

(b) Consider now the

linear system of equations

with

Use again standard Gaussian elimination and compute the result analytically. Compare

thereafter your analytical results with the numerical ones obtained using the programs in

the program library.

is real, symmetric and positive deﬁnite, then it has a unique factorization

(called Cholesky factorization)

where is the upper matrix, implying that

. The algorithm for the Cholesky decomposition is a special case of the general LU-

decomposition algorithm. The algorithm of this decomposition is as follows

Calculate the diagonal element by setting up a loop for to (C++

indexing of matrices and vectors)

(5.24)

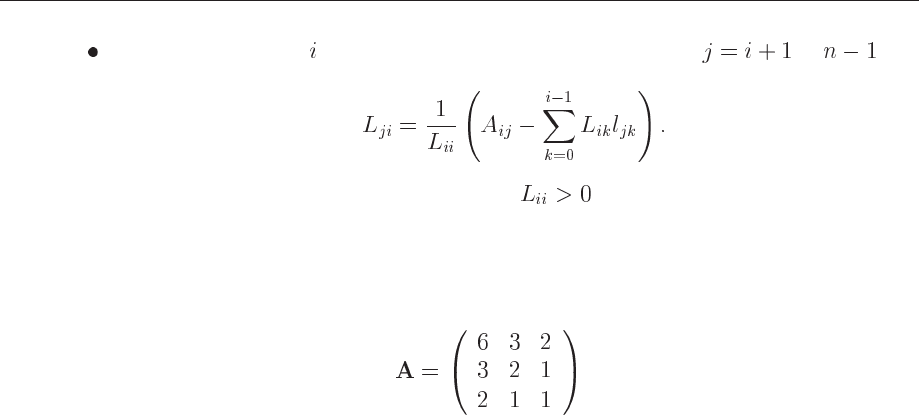
5.6. PROJECT: MATRIX OPERATIONS 85

within the loop over , introduce a new loop which goes from to and

calculate

(5.25)

For the Cholesky algorithm we have always that

and the problem with exceedingly

large matrix elements does not appear and hence there is no need for pivoting. Write

a function which performs the Cholesky decomposition. Test your program against the

standard LU decomposition by using the matrix

(5.26)

Are the matrices in exercises a) and b) positive deﬁnite? If so, employ your function for

Cholesky decomposition and compare your results with those from LU-decomposition.

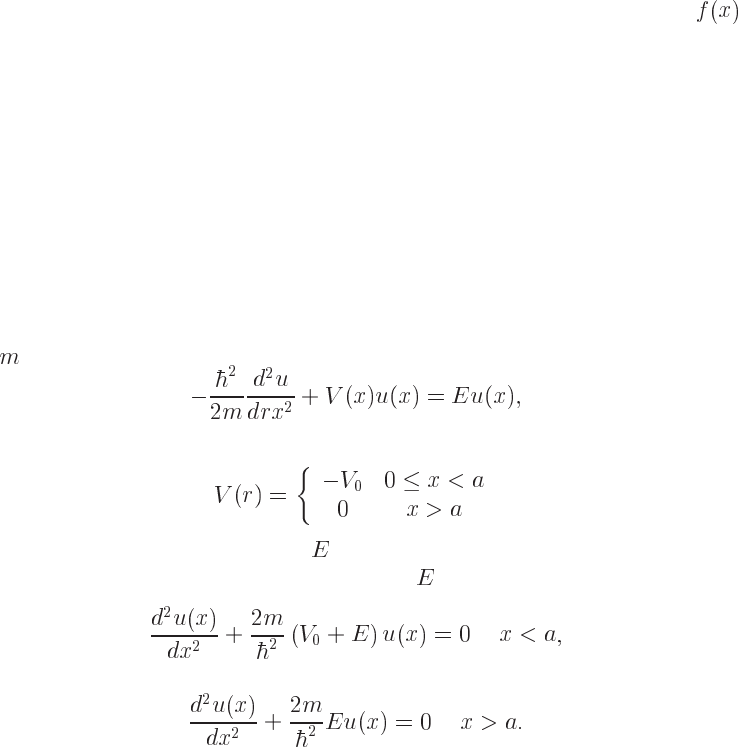
Chapter 6

Non-linear equations and roots of

polynomials

6.1 Introduction

In Physics we often encounter the problem of determining the root of a function

. Espe-

cially, we may need to solve non-linear equations of one variable. Such equations are usually

divided into two classes, algebraic equations involving roots of polynomials and transcendental

equations. When there is only one independent variable, the problem is one-dimensional, namely

to ﬁnd the root or roots of a function. Except in linear problems, root ﬁnding invariably proceeds

by iteration, and this is equally true in one or in many dimensions. This means that we cannot

solve exactly the equations at hand. Rather, we start with some approximate trial solution. The

chosen algorithm will in turn improve the solution until some predetermined convergence cri-

terion is satisﬁed. The algoritms we discuss below attempt to implement this strategy. We will

deal mainly with one-dimensional problems. The methods

You may have encountered examples of so-called transcendental equations when solving the

Schrödinger equation (SE) for a particle in a box potential. The one-dimensional SE for a particle

with mass

(6.1)

and our potential is deﬁned as

(6.2)

Bound states correspond to negativeenergy

and scattering states are givenby positiveenergies.

The SE takes the form (without specifying the sign of )

(6.3)

and

(6.4)

88 CHAPTER 6. NON-LINEAR EQUATIONS AND ROOTS OF POLYNOMIALS

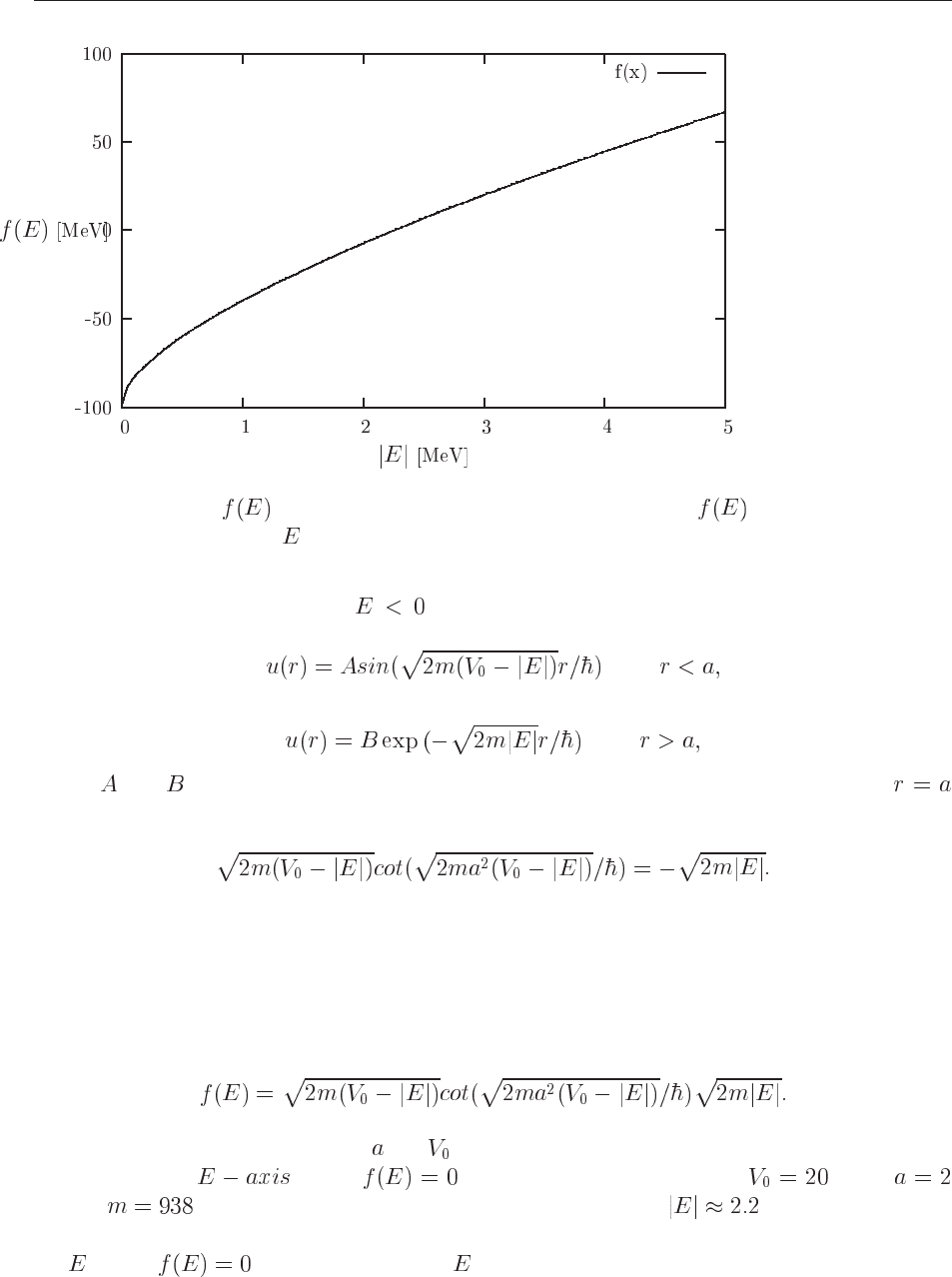
Figure 6.1: Plot of Eq. (6.8) as function of energy |E| in MeV. has dimension MeV.

Note well that the energy is for bound states.

If we specialize to bound states

and implement the boundary conditions on the wave

function we obtain

(6.5)

and

(6.6)

where

and are constants. Using the continuity requirement on the wave function at

one obtains the transcendental equation

(6.7)

This equation is an example of the kind of equations which could be solved by some of the

methods discussed below. The algorithms we discuss are the bisection method, the secant, false

position and Brent’s methods and Newton-Raphson’s method. Moreover, we will also discuss

how to ﬁnd roots of polynomials in section 6.6.

In order to ﬁnd the solution for Eq. (6.7), a simple procedure is to deﬁne a function

(6.8)

and with chosen or given values for

and make a plot of this function and ﬁnd the approximate

region along the where . We show this in Fig. 6.1 for MeV,

fm and MeV. Fig. 6.1 tells us that the solution is close to (the binding energy

of the deuteron). The methods we discuss below are then meant to give us a numerical solution

for where is satisﬁed and with determined by a given numerical precision.