Hjorth-Jensen M. Computational Physics
Подождите немного. Документ загружается.

COMPUTATIONAL PHYSICS
M. Hjorth-Jensen
Department of Physics, University of Oslo, 2003

iii
Preface
In 1999, when we started teaching this course at the Department of Physics in Oslo, Compu-
tational Physics and Computational Science in general were still perceived by the majority of
physicists and scientists as topics dealing with just mere tools and number crunching, and not as
subjects of their own. The computational background of most students enlisting for the course
on computational physics could span from dedicated hackers and computer freaks to people who
basically had never used a PC. The majority of graduate students had a very rudimentary knowl-
edge of computational techniques and methods. Four years later most students have had a fairly
uniform introduction to computers, basic programming skills and use of numerical exercises in
undergraduate courses. Practically every undergraduate student in physics has now made a Mat-
lab or Maple simulation of e.g., the pendulum, with or without chaotic motion. These exercises
underscore the importance of simulations as a means to gain novel insights into physical sys-
tems, especially for those cases where no analytical solutions can be found or an experiment
is to complicated or expensive to carry out. Thus, computer simulations are nowadays an inte-
gral part of contemporary basic and applied research in the physical sciences. Computation is
becoming as important as theory and experiment. We could even strengthen this statement by
saying that computational physics, theoretical physics and experimental are all equally important
in our daily research and studies of physical systems. Physics is nowadays the unity of theory,
experiment and computation. The ability "to compute" is now part of the essential repertoire of
research scientists. Several new fields have emerged and strengthened their positions in the last
years, such as computational materials science, bioinformatics, computational mathematics and
mechanics, computational chemistry and physics and so forth, just to mention a few. To be able
to e.g., simulate quantal systems will be of great importance for future directions in fields like
materials science and nanotechonology.
This ability combines knowledge from many different subjects, in our case essentially from
the physical sciences, numerical analysis, computing languages and some knowledge of comput-
ers. These topics are, almost as a rule of thumb, taught in different, and we would like to add,
disconnected courses. Only at the levelofthesis work is the student confronted with the synthesis
of all these subjects, and then in a bewildering and disparate manner, trying to e.g., understand
old Fortran 77 codes inherited from his/her supervisor back in the good old ages, or even more
archaic, programs. Hours may have elapsed in front of a screen which just says ’Underflow’, or
’Bus error’, etc etc, without fully understanding what goes on. Porting the program to another
machine could even result in totally different results!
The first aim of this course is therefore to bridge the gap between undergraduate courses
in the physical sciences and the applications of the aquired knowledge to a given project, be it
either a thesis work or an industrial project. We expect you to have some basic knowledge in the
physical sciences, especially within mathematics and physics through e.g., sophomore courses
in basic calculus, linear algebraand general physics. Furthermore, having taken an introductory
course on programming is something we recommend. As such, an optimal timing for taking this
course, would be when you are close to embark on a thesis work, or if you’ve just started with a
thesis. But obviously, you should feel free to choose your own timing.
We have several other aims as well in addition to prepare you for a thesis work, namely

iv
We would like to give you an opportunity to gain a deeper understanding of the physics
you have learned in other courses. In most courses one is normally confronted with simple
systems which provide exact solutions and mimic to a certain extent the realistic cases.
Many are however the comments like ’why can’t we do something else than the box po-
tential?’. In several of the projects we hope to present some more ’realistic’ cases to solve
by various numerical methods. This also means that we wish to give examples of how
physics can be applied in a much broader context than it is discussed in the traditional
physics undergraduate curriculum.
To encourage you to "discover" physics in a way similar to how researchers learn in the
context of research.
Hopefully also to introduce numerical methods and new areas of physics that can be stud-
ied with the methods discussed.
To teach structured programming in the context of doing science.
The projects we propose are meant to mimic to a certain extent the situation encountered
during a thesis or project work. You will tipically have at your disposal 1-2 weeks to solve
numerically a given project. In so doing you may need to do a literature study as well.
Finally, we would like you to write a report for every project.
The exam reflects this project-like philosophy. The exam itself is a project which lasts one
month. You have to hand in a report on a specific problem, and your report forms the basis
for an oral examination with a final grading.
Our overall goal is to encourage you to learn about science through experience and by asking
questions. Our objective is always understanding, not the generation of numbers. The purpose
of computing is further insight, not mere numbers! Moreover, and this is our personal bias, to
device an algorithm and thereafter write a code for solving physics problems is a marvelous way
of gaining insight into complicated physical systems. The algorithm you end up writing reflects
in essentially all cases your own understanding of the physics of the problem.
Most of you are by now familiar, through various undergraduate courses in physics and math-
ematics, with interpreted languages such as Maple, Mathlab and Mathematica. In addition, the
interest in scripting languages such as Python or Perl has increased considerably in recent years.
The modern programmer would typically combine several tools, computing environments and
programming languages. A typical example is the following. Suppose you are working on a
project which demands extensive visualizations of the results. To obtain these results you need
however a programme which is fairly fast when computational speed matters. In this case you
would most likely write a high-performance computing programme in languages which are tay-
lored for that. These are represented by programming languages like Fortran 90/95 and C/C++.
However, to visualize the results you would find interpreted languages like e.g., Matlab or script-
ing languages like Python extremely suitable for your tasks. You will therefore end up writing
e.g., a script in Matlab which calls a Fortran 90/95 ot C/C++ programme where the number
crunching is done and then visualize the results of say a wave equation solver via Matlab’s large

v
library of visualization tools. Alternatively, you could organize everything into a Python or Perl
script which does everything for you, calls the Fortran 90/95 or C/C++ programs and performs
the visualization in Matlab as well.
Being multilingual is thus a feature which not only applies to modern society but to comput-
ing environments as well.
However, there is more to the picture than meets the eye. This course emphasizes the use of
programming languages like Fortran 90/95 and C/C++ instead of interpreted ones like Matlab or
Maple. Computational speed is not the only reason for this choice of programming languages.
The main reason is that we feel at a certain stage one needs to have some insights into the algo-
rithm used, its stability conditions, possible pitfalls like loss of precision, ranges of applicability
etc. Although we will at various stages recommend the use of library routines for say linear
algebra
1
, our belief is that one should understand what the given function does, at least to have
a mere idea. From such a starting point we do further believe that it can be easier to develope
more complicated programs, on your own. We do therefore devote some space to the algorithms
behind various functions presented in the text. Especially, insight into how errors propagate and
how to avoid them is a topic we’d like you to pay special attention to. Only then can you avoid
problems like underflow, overflow and loss of precision. Such a control is not always achievable
with interpreted languages and canned functions where the underlying algorithm
Needless to say, these lecture notes are upgraded continuously, from typos to new input. And
we do always benifit from your comments, suggestions and ideas for making these notes better.
It’s through the scientific discourse and critics we advance.
1
Such library functions are often taylored to a given machine’s architecture and should accordingly run faster
than user provided ones.
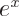
Contents
I Introduction to Computational Physics 1
1 Introduction 3
1.1 Choice of programming language . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2 Designing programs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2 Introduction to C/C++ and Fortran 90/95 9
2.1 Getting started . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.1.1 Representation of integer numbers . . . . . . . . . . . . . . . . . . . . . 15
2.2 Real numbers and numerical precision . . . . . . . . . . . . . . . . . . . . . . . 18
2.2.1 Representation of real numbers . . . . . . . . . . . . . . . . . . . . . . 19
2.2.2 Further examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.3 Loss of precision . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.3.1 Machine numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.3.2 Floating-point error analysis . . . . . . . . . . . . . . . . . . . . . . . . 32
2.4 Additional features of C/C++ and Fortran 90/95 . . . . . . . . . . . . . . . . . . 33
2.4.1 Operators in C/C++ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.4.2 Pointers and arrays in C/C++. . . . . . . . . . . . . . . . . . . . . . . . 35
2.4.3 Macros in C/C++ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
2.4.4 Structures in C/C++ and TYPE in Fortran 90/95 . . . . . . . . . . . . . 39
3 Numerical differentiation 41
3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3.2 Numerical differentiation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3.2.1 The second derivative of
. . . . . . . . . . . . . . . . . . . . . . . . . 45
3.2.2 Error analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
3.2.3 How to make figures with Gnuplot . . . . . . . . . . . . . . . . . . . . . 54
3.3 Richardson’s deferred extrapolation method . . . . . . . . . . . . . . . . . . . . 57
4 Classes, templates and modules 61
4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
4.2 A first encounter, the vector class . . . . . . . . . . . . . . . . . . . . . . . . . . 62
4.3 Classes and templates in C++ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
4.4 Using Blitz++ with vectors and matrices . . . . . . . . . . . . . . . . . . . . . . 68
vii

viii CONTENTS
4.5 Building new classes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
4.6 MODULE and TYPE declarations in Fortran 90/95 . . . . . . . . . . . . . . . . 68
4.7 Object orienting in Fortran 90/95 . . . . . . . . . . . . . . . . . . . . . . . . . . 68
4.8 An example of use of classes in C++ and Modules in Fortran 90/95 . . . . . . . . 68
5 Linear algebra 69
5.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
5.2 Programming details . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
5.2.1 Declaration of fixed-sized vectors and matrices . . . . . . . . . . . . . . 70
5.2.2 Runtime declarations of vectors and matrices . . . . . . . . . . . . . . . 72
5.2.3 Fortran features of matrix handling . . . . . . . . . . . . . . . . . . . . 75
5.3 LU decomposition of a matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
5.4 Solution of linear systems of equations . . . . . . . . . . . . . . . . . . . . . . . 80
5.5 Inverse of a matrix and the determinant . . . . . . . . . . . . . . . . . . . . . . 81
5.6 Project: Matrix operations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
6 Non-linear equations and roots of polynomials 87
6.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
6.2 Iteration methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
6.3 Bisection method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
6.4 Newton-Raphson’s method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
6.5 The secant method and other methods . . . . . . . . . . . . . . . . . . . . . . . 94
6.5.1 Calling the various functions . . . . . . . . . . . . . . . . . . . . . . . . 97
6.6 Roots of polynomials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
6.6.1 Polynomials division . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
6.6.2 Root finding by Newton-Raphson’s method . . . . . . . . . . . . . . . . 97
6.6.3 Root finding by deflation . . . . . . . . . . . . . . . . . . . . . . . . . . 97
6.6.4 Bairstow’s method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
7 Numerical interpolation, extrapolation and fitting of data 99
7.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
7.2 Interpolation and extrapolation . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
7.2.1 Polynomial interpolation and extrapolation . . . . . . . . . . . . . . . . 99
7.3 Qubic spline interpolation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
8 Numerical integration 105
8.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
8.2 Equal step methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
8.3 Gaussian quadrature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
8.3.1 Orthogonal polynomials, Legendre . . . . . . . . . . . . . . . . . . . . 112
8.3.2 Mesh points and weights with orthogonal polynomials . . . . . . . . . . 115
8.3.3 Application to the case
. . . . . . . . . . . . . . . . . . . . . . . 116
8.3.4 General integration intervals for Gauss-Legendre . . . . . . . . . . . . . 117

CONTENTS ix
8.3.5 Other orthogonal polynomials . . . . . . . . . . . . . . . . . . . . . . . 118
8.3.6 Applications to selected integrals . . . . . . . . . . . . . . . . . . . . . 120
8.4 Treatment of singular Integrals . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
9 Outline of the Monte-Carlo strategy 127
9.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
9.1.1 First illustration of the use of Monte-Carlo methods, crude integration . . 129
9.1.2 Second illustration, particles in a box . . . . . . . . . . . . . . . . . . . 134
9.1.3 Radioactive decay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136
9.1.4 Program example for radioactive decay of one type of nucleus . . . . . . 137
9.1.5 Brief summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
9.2 Physics Project: Decay of
Bi and Po . . . . . . . . . . . . . . . . . . . . . 140
9.3 Random numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141
9.3.1 Properties of selected random number generators . . . . . . . . . . . . . 144
9.4 Probability distribution functions . . . . . . . . . . . . . . . . . . . . . . . . . . 146
9.4.1 The central limit theorem . . . . . . . . . . . . . . . . . . . . . . . . . . 148
9.5 Improved Monte Carlo integration . . . . . . . . . . . . . . . . . . . . . . . . . 149
9.5.1 Change of variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151
9.5.2 Importance sampling . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
9.5.3 Acceptance-Rejection method . . . . . . . . . . . . . . . . . . . . . . . 157
9.6 Monte Carlo integration of multidimensional integrals . . . . . . . . . . . . . . . 157
9.6.1 Brute force integration . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
9.6.2 Importance sampling . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160
10 Random walks and the Metropolis algorithm 163
10.1 Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163
10.2 Diffusion equation and random walks . . . . . . . . . . . . . . . . . . . . . . . 164
10.2.1 Diffusion equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164
10.2.2 Random walks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
10.3 Microscopic derivation of the diffusion equation . . . . . . . . . . . . . . . . . . 172
10.3.1 Discretized diffusion equation and Markov chains . . . . . . . . . . . . . 172
10.3.2 Continuous equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176
10.3.3 Numerical simulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177
10.4 The Metropolis algorithm and detailed balance . . . . . . . . . . . . . . . . . . 180
10.5 Physics project: simulation of the Boltzmann distribution . . . . . . . . . . . . . 184
11 Monte Carlo methods in statistical physics 187
11.1 Phase transitions in magnetic systems . . . . . . . . . . . . . . . . . . . . . . . 187
11.1.1 Theoretical background . . . . . . . . . . . . . . . . . . . . . . . . . . 187
11.1.2 The Metropolis algorithm . . . . . . . . . . . . . . . . . . . . . . . . . 193
11.2 Program example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 195
11.2.1 Program for the two-dimensional Ising Model . . . . . . . . . . . . . . . 195
11.3 Selected results for the Ising model . . . . . . . . . . . . . . . . . . . . . . . . . 199

x CONTENTS
11.3.1 Phase transitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 199
11.3.2 Heat capacity and susceptibility as functions of number of spins . . . . . 200
11.3.3 Thermalization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
11.4 Other spin models . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
11.4.1 Potts model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
11.4.2 XY-model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
11.5 Physics project: simulation of the Ising model . . . . . . . . . . . . . . . . . . . 201
12 Quantum Monte Carlo methods 203
12.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
12.2 Variational Monte Carlo for quantum mechanical systems . . . . . . . . . . . . . 204
12.2.1 First illustrationofVMC methods, the one-dimensionalharmonic oscillator206
12.2.2 The hydrogen atom . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209
12.2.3 Metropolis sampling for the hydrogen atom and the harmonic oscillator . 211
12.2.4 A nucleon in a gaussian potential . . . . . . . . . . . . . . . . . . . . . 215
12.2.5 The helium atom . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216
12.2.6 Program example for atomic systems . . . . . . . . . . . . . . . . . . . 221
12.3 Simulation of molecular systems . . . . . . . . . . . . . . . . . . . . . . . . . . 228
12.3.1 The H
molecule . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228
12.3.2 Physics project: the H
molecule . . . . . . . . . . . . . . . . . . . . . . 230
12.4 Many-body systems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 230
12.4.1 Liquid He . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 230
12.4.2 Bose-Einstein condensation . . . . . . . . . . . . . . . . . . . . . . . . 232
12.4.3 Quantum dots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233
12.4.4 Multi-electron atoms . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233
13 Eigensystems 235
13.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235
13.2 Eigenvalue problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235
13.2.1 Similarity transformations . . . . . . . . . . . . . . . . . . . . . . . . . 236
13.2.2 Jacobi’s method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 237
13.2.3 Diagonalization through the Householder’s method for tri-diagonalization 238
13.3 Schrödinger’s equation (SE) through diagonalization . . . . . . . . . . . . . . . 241
13.4 Physics projects: Bound states in momentum space . . . . . . . . . . . . . . . . 248
13.5 Physics projects: Quantum mechanical scattering . . . . . . . . . . . . . . . . . 251
14 Differential equations 255
14.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
14.2 Ordinary differential equations (ODE) . . . . . . . . . . . . . . . . . . . . . . . 255
14.3 Finite difference methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 257
14.3.1 Improvements to Euler’s algorithm, higher-order methods . . . . . . . . 259
14.4 More on finite difference methods, Runge-Kutta methods . . . . . . . . . . . . . 260
14.5 Adaptive Runge-Kutta and multistep methods . . . . . . . . . . . . . . . . . . . 261
