Hirsch M., Smale S., Devaney R., Differential Equations, Dynamical Systems, and an Introduction to Chaos
Подождите немного. Документ загружается.


266 Chapter 12 Applications in Circuit Theory
m
⫹
g
⫹
m
⫺
(1, 0)
y
*
y
a(y)
Figure 12.5 The
semi-Poincaré map.
about the origin. This implies that if (x(t ), y(t )) is a solution curve, then so is
(−x(t ), −y(t)).
Part of the graph of δ(y) is shown schematically in Figure 12.6. The interme-
diate value theorem and the proposition imply that there is a unique y
0
∈ v
+
with δ(y
0
) = 0. Consequently, α(y
0
) =−y
0
and it follows from the skew-
symmetry that the solution through (0, y
0
) is periodic. Since δ(y) = 0 except
at y
0
, we have α(y) = y for all other y-values, and so it follows that φ
t
(0, y
0
)
is the unique periodic solution.
We next show that all other solutions (except the equilibrium point) tend
to this periodic solution. Toward that end, we define a map β : v
−
→ v
+
,
sending each point of v
−
to the first intersection of the solution (for t>0)
with v
+
. By symmetry we have
β(y) =−α(−y).
Note also that P(y) = β ◦α(y).
y
*
y
0
y
d(y)
Figure 12.6 The
graph of δ(y).
12.3 The van der Pol Equation 267
We identify the y-axis with the real numbers in the y coordinate. Thus if
y
1
, y
2
∈ v
+
∪ v
−
we write y
1
>y
2
if y
1
is above y
2
. Note that α and β reverse
this ordering while P preserves it.
Now choose y ∈ v
+
with y>y
0
. Since α(y
0
) =−y
0
we have α(y) < −y
0
and P(y) >y
0
. On the other hand, δ(y) < 0, which implies that α(y) > −y.
Therefore P(y) = β(α(y)) <y. We have shown that y>y
0
implies y>P(y) >
y
0
. Similarly P(y) >P(P(y)) >y
0
and by induction P
n
(y) >P
n+1
(y) >y
0
for all n>0.
The decreasing sequence P
n
(y) has a limit y
1
≥ y
0
in v
+
. Note that y
1
is a
fixed point of P, because, by continuity of P, we have
P(y
1
) − y
1
= lim
n→∞
P(P
n
(y)) − y
1
= y
1
− y
1
= 0.
Since P has only one fixed point, we have y
1
= y
0
. This shows that the solution
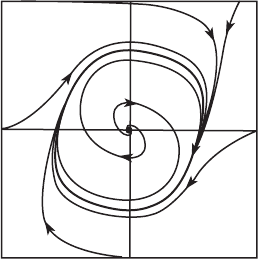
through y spirals toward the periodic solution as t →∞. See Figure 12.7. The
same is true if y<y
0
; the details are left to the reader. Since every solution
except the equilibrium meets v
+
, the proof of the theorem is complete.
Finally, we turn to the proof of the proposition. We adopt the following
notation. Let γ :[a, b]→
R
2
be a smooth curve in the plane and let F : R
2
→
R. We write γ (t ) = (x(t ), y(t)) and define
γ
F(x, y) =
b
a
F(x(t ), y(t )) dt .
Figure 12.7 The phase
portrait of the van der Pol
equation.
268 Chapter 12 Applications in Circuit Theory
If it happens that x
(t) = 0 for a ≤ t ≤ b, then along γ , y is a function of x,
so we may write y = y(x). In this case we can change variables:
b
a
F(x(t ), y(t )) dt =
x(b)
x(a)
F(x, y(x))
dt
dx
dx.
Therefore
γ
F(x, y) =
x(b)
x(a)
F(x, y(x))
dx/dt
dx.
We have a similar expression if y
(t) = 0.
Now recall the function
W (x, y) =
1
2
x
2
+ y
2
introduced in the previous section. Let p ∈ v
+
. Suppose α(p) = φ
τ
(p). Let
γ (t ) = (x(t ), y(t )) for 0 ≤ t ≤ τ = τ (p) be the solution curve joining p ∈ v
+
to α(p) ∈ v
−
. By definition
δ(p) =
1
2
y(τ )
2
− y(0)
2
= W (x(τ ), y(τ )) − W (x(0), y(0)).
Thus
δ(p) =
τ
0
d
dt
W (x(t ), y(t)) dt .
Recall from Section 12.2 that we have
˙
W =−xf (x) =−x(x
3
− x).
Thus we have
δ(p) =
τ
0
−x(t )(x(t )
3
− x(t )) dt
=
τ
0
x(t )
2
(1 − x(t)
2
) dt .
This immediately proves part (1) of the proposition because the integrand is
positive for 0 <x(t ) < 1.

12.3 The van der Pol Equation 269
g
⫹
y
1
y
2
y
0
c
3
c
2
c
1
Figure 12.8 The curves γ
1
, γ
2
,
and γ
3
depicted on the closed
orbit through y
0
.
We may rewrite the last equality as
δ(p) =
γ
x
2
1 − x
2
.
We restrict attention to points p ∈ v
+
with p>y
∗
. We divide the correspond-
ing solution curve γ into three curves γ
1
, γ
2
, γ
3
as displayed in Figure 12.8.
The curves γ
1
and γ
3
are defined for 0 ≤ x ≤ 1, while the curve γ
2
is defined
for y
1
≤ y ≤ y
2
. Then
δ(p) = δ
1
(p) + δ
2
(p) + δ
3
(p)
where
δ
i
(p) =
γ
i
x
2
1 − x
2
, i = 1, 2, 3.
Notice that, along γ
1
, y(t ) may be regarded as a function of x. Hence we have
δ
1
(p) =
1
0
x
2
1 − x
2
dx/dt
dx
=
1
0
x
2
1 − x
2
y − f (x)
dx
where f (x) = x
3
− x.Asp moves up the y-axis, y − f (x) increases [for (x, y)
on γ
1
]. Hence δ
1
(p) decreases as p increases. Similarly δ
3
(p) decreases as p
increases.

270 Chapter 12 Applications in Circuit Theory
On γ
2
, x(t ) may be regarded as a function of y, which is defined for y ∈
[y
1
, y
2
] and x ≥ 1. Therefore since dy/dt =−x, we have
δ
2
(p) =
y
1
y
2
−x(y)
1 − x(y)
2
dy
=
y
2
y
1
x(y)
1 − x(y)
2
dy
so that δ
2
(p) is negative.
As p increases, the domain [y
1
, y
2
] of integration becomes steadily larger.
The function y → x(y) depends on p, so we write it as x
p
(y). As p
increases, the curves γ
2
move to the right; hence x
p
(y) increases and so
x
p
(y)(1 − x
p
(y)
2
) decreases. It follows that δ
2
(p) decreases as p increases;
and evidently lim
p→∞
δ
2
(p) =−∞. Consequently, δ(p) also decreases and
tends to −∞ as p →∞. This completes the proof of the proposition.
12.4 A Hopf Bifurcation
We now describe a more general class of circuit equations where the resistor
characteristic depends on a parameter μ and is denoted by f
μ
. (Perhaps μ is
the temperature of the resistor.) The physical behavior of the circuit is then
described by the system of differential equations on
R
2
:
dx
dt
= y − f
μ
(x)
dy
dt
=−x.
Consider as an example the special case where f
μ
is described by
f
μ
(x) = x
3
− μx
and the parameter μ lies in the interval [−1, 1]. When μ = 1 we have the
van der Pol system from the previous section. As before, the only equilibrium
point lies at the origin. The linearized system is
Y
=
μ 1
−10
Y ,
12.4 A Hopf Bifurcation 271
and the eigenvalues are
λ
±
=
1
2
μ ±
μ
2
− 4
.
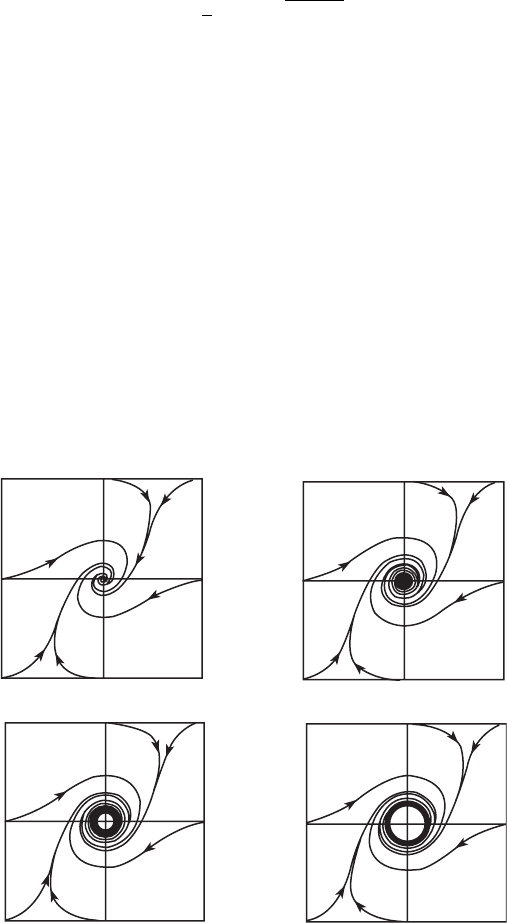
Thus the origin is a spiral sink for −1 ≤ μ < 0 and a spiral source for
0 < μ ≤ 1. Indeed, when −1 ≤ μ ≤ 0, the resistor is passive as the graph of f
μ
lies in the first and third quadrants. Therefore all solutions tend to the origin in
this case. This holds even in the case where μ = 0 and the linearization yields
a center. Physically the circuit is dead in that, after a period of transition, all
currents and voltages stay at 0 (or as close to 0 as we want).
However, as μ becomes positive, the circuit becomes alive. It begins to
oscillate. This follows from the fact that the analysis of Section 12.3 applies
to this system for all μ in the interval (0, 1]. We therefore see the birth of
a (unique) periodic solution γ
μ
as μ increases through 0 (see Exercise 4 at
the end of this chapter). Just as above, this solution attracts all other nonzero
solutions. As in Section 8.5, this is an example of a Hopf bifurcation. Further
elaboration of the ideas in Section 12.3 can be used to show that γ
μ
→ 0as
μ → 0 with μ > 0. Figure 12.9 shows some phase portraits associated to this
bifurcation.
l⫽⫺0.5 l⫽⫺0.1
l⫽0.05 l⫽0.2
Figure 12.9 The Hopf bifurcation in the system x
= y −
x
3
+ μ x, y
= −x.

272 Chapter 12 Applications in Circuit Theory
12.5 Exploration: Neurodynamics
One of the most important developments in the study of the firing of nerve
cells or neurons was the development of a model for this phenomenon in
giant squid in the 1950s by Hodgkin and Huxley [23]. They developed a four-
dimensional system of differential equations that described the electrochemical
transmission of neuronal signals along the cell membrane, a work for which
they later received the Nobel prize. Roughly speaking, this system is similar
to systems that arise in electrical circuits. The neuron consists of a cell body,
or soma, which receives electrical stimuli. This stimulus is then conducted
along the axon, which can be thought of as an electrical cable that connects to
other neurons via a collection of synapses. Of course, the motion is not really
electrical, because the current is not really made up of electrons, but rather
ions (predominantly sodium and potassium). See [15] or [34] for a primer on
the neurobiology behind these systems.
The four-dimensional Hodgkin-Huxley system is difficult to deal with,
primarily because of the highly nonlinear nature of the equations. An impor-
tant breakthrough from a mathematical point of view was achieved by
Fitzhugh [18] and Nagumo et al. [35], who produced a simpler model of
the Hodgkin-Huxley model. Although this system is not as biologically accu-
rate as the original system, it nevertheless does capture the essential behavior
of nerve impulses, including the phenomenon of excitability alluded to below.
The Fitzhugh-Nagumo system of equations is given by
x
= y + x −
x
3
3
+ I
y
=−x + a − by
where a and b are constants satisfying
0 <
3
2
(1 − a) <b<1
and I is a parameter. In these equations x is similar to the voltage and rep-
resents the excitability of the system; the variable y represents a combination
of other forces that tend to return the system to rest. The parameter I is a
stimulus parameter that leads to excitation of the system; I is like an applied
current. Note the similarity of these equations with the van der Pol equation
of Section 12.3.
1. First assume that I = 0. Prove that this system has a unique equilibrium
point (x
0
, y
0
). Hint: Use the geometry of the nullclines for this rather than

Exercises 273
explicitly solving the equations. Also remember the restrictions placed on
a and b.
2. Prove that this equilibrium point is always a sink.
3. Now suppose that I = 0. Prove that there is still a unique equilibrium
point (x
I
, y
I
) and that x
I
varies monotonically with I .
4. Determine values of x
I
for which the equilibrium point is a source and
show that there must be a stable limit cycle in this case.
5. When I = 0, the point (x
0
, y
0
) is no longer an equilibrium point.
Nonetheless we can still consider the solution through this point. Describe
the qualitative nature of this solution as I moves away from 0. Explain
in mathematical terms why biologists consider this phenomenon the
“excitement” of the neuron.
6. Consider the special case where a = I = 0. Describe the phase plane for
each b>0 (no longer restrict to b<1) as completely as possible. Describe
any bifurcations that occur.
7. Now let I vary as well and again describe any bifurcations that occur.
Describe in as much detail as possible the phase portraits that occur in the
I, b–plane, with b>0.
8. Extend the analysis of the previous problem to the case b ≤ 0.
9. Now fix b = 0 and let a and I vary. Sketch the bifurcation plane (the
I, a–plane) in this case.
EXERCISES
1. Find the phase portrait for the differential equation
x
= y − f (x), f (x) = x
2
,
y
=−x.
Hint: Exploit the symmetry about the y-axis.
2. Let
f (x) =
⎧
⎨
⎩
2x − 3ifx>1
−x if −1 ≤ x ≤ 1
2x + 3ifx<−1.
Consider the system
x
= y − f (x)
y
=−x.
(a) Sketch the phase plane for this system.
(b) Prove that this system has a unique closed orbit.
274 Chapter 12 Applications in Circuit Theory
3. Let
f
a
(x) =
⎧
⎨
⎩
2x + a − 2ifx>1
ax if −1 ≤ x ≤ 1
2x − a + 2ifx<−1.
Consider the system
x
= y − f
a
(x)
y
=−x.
(a) Sketch the phase plane for this system for various values of a.
(b) Describe the bifurcation that occurs when a = 0.
4. Consider the system described in Section 12.4
x
= y − (x
3
− μx)
y
=−x
where the parameter μ satisfies 0 ≤ μ < 1. Fill in the details of the proof
that a Hopf bifurcation occurs at μ = 0.
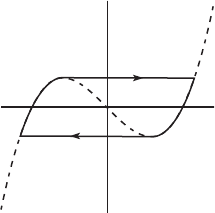
5. Consider the system
x
= μ(y − (x
3
− x)), μ > 0
y
=−x.
Prove that this system has a unique nontrivial periodic solution γ
μ
. Show
that as μ →∞, γ
μ
tends to the closed curve consisting of two horizontal
line segments and two arcs on y = x
3
− x as in Figure 12.10. This type
of solution is called a relaxation oscillation. When μ is large, there are
two quite different timescales along the periodic solution. When moving
horizontally, we have x
very large, and so the solution makes this transit
Figure 12.10
Exercises 275
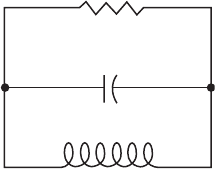
R
C
L
Figure 12.11
very quickly. On the other hand, near the cubic nullcline, x
= 0 while y
is bounded. Hence this transit is comparatively much slower.
6. Find the differential equations for the network in Figure 12.11, where the
resistor is voltage controlled; that is, the resistor characteristic is the graph
of a function g :
R → R, i
R
= g (v
R
).
7. Show that the LC circuit consisting of one inductor and one capacitor
wired in a closed loop oscillates.
8. Determine the phase portrait of the following differential equation and in
particular show there is a unique nontrivial periodic solution:
x
= y − f (x)
y
=−g (x)
where all of the following are assumed:
(a) g (−x) =−g (x) and xg (x) > 0 for all x = 0;
(b) f (−x) =−f (x) and f (x) < 0 for 0 <x<a;
(c) for x>a, f (x) is positive and increasing;
(d) f (x) →∞as x →∞.
9. Consider the system
x
= y
y
= a(1 − x
4
)y − x
(a) Find all equilibrium points and classify them.
(b) Sketch the phase plane.
(c) Describe the bifurcation that occurs when a becomes positive.
(d) Prove that there exists a unique closed orbit for this system when
a>0.
(e) Show that all nonzero solutions of the system tend to this closed orbit
when a>0.
